Ищем значение числа Пи, используя генератор случайных значений29.10.2022 22:17

Представьте, что у вас есть функция random (), которая генерируют случайным образом значения в промежутке [0;1]

Вычислите значение числа \pi

Это один из популярных вопросов на собеседовании в топовую IT компанию

В первую секунду может показаться, что ваш интервьюер слегка издевается над вам, но если вспомнить основы из теории вероятности, то все становится гораздо проще. Let’s go!

База из теории вероятности

Классическое определение вероятности.

Вероятность, что событие A произойдет, равно отношению количеству благоприятных исходов mк количеству всех возможных исходов n

На языке математики это выглядит так: P(A) = \frac{m}{n}

Например у нас есть кубик. Какая вероятность что выпадет грань с четными значениями?

Решение

Геометрическое определение вероятности.

Предыдущее определение вероятности отличное, но оно обладает несколькими существенными ограничениями. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. 

Чтобы стало понятно о чем речь — давайте решим задачку.

На отрезок [0;1]случайным образом брошена точка M.Найдите вероятность того, что она попадет в промежуток [0,5; 0,8]

Понятно, что здесь не получится использовать классическое определение, поскольку на отрезке бесконечно много точек. Тогда нам идет на помощь геометрическое определение

вероятности P(A)=\frac{S(A)}{S(\Omega)}, в нашем случае S(A) = 0.8 - 0.5=0.3, S(\Omega)=1

Следовательно P(A)=0,3

Решение задачи

Концепция

Построим геометрическую модель.

Введем систему координат с осями xи y
Расположим квадрат с единичной стороной, так чтобы начало системы координат находилось в левом углу.
Нарисуем единичный круг с центром в начале координат.

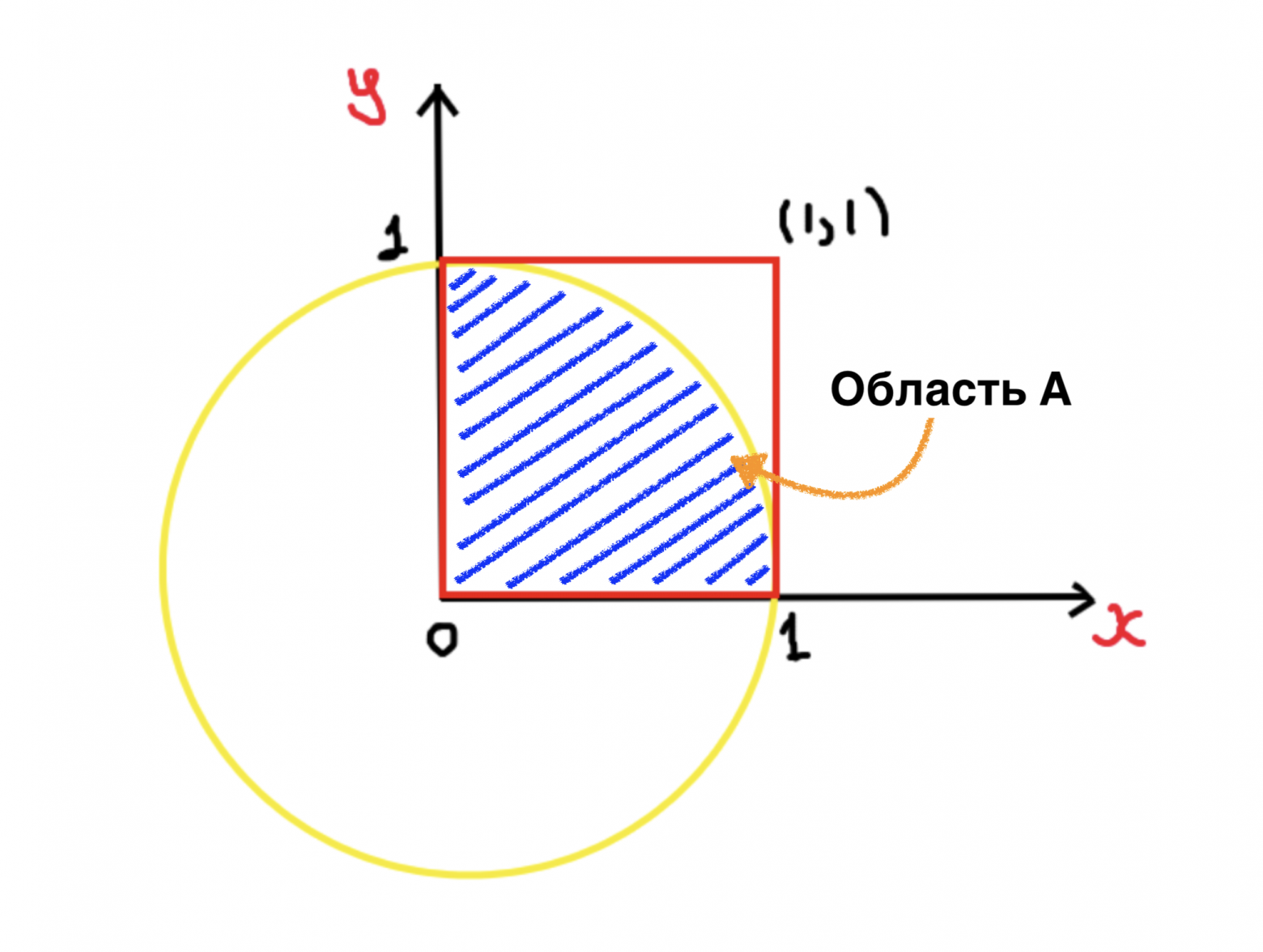геометрическая модельгеометрическая модель

Будем случайным образом располагать точку в квадрате.
Наша исходная задача сводится к следующему вопросу.
Какая вероятность, что точка попадет в верхнюю правую четверть круга (область A)

Мы знаем, что S_{квадрата} = 1, а S_{A} =\frac{\pi r^2}{4}=(r=1)=\frac{\pi}{4}

Значит вероятность того, что точка попадет в искомую область равна P(A)=\frac{\pi}{4}

С другой стороны, после распределения n точек по квадрату, мы можем оценить количество точек, которое попало внутрь круга. Для этого точка с координатами (x,y)

должна удовлетворять неравенству \sqrt{x^2+y^2}\leq1

Тогда вероятность P(A)=\frac{m}{n}, где mколичество точек попавших внутрь круга, а n общее число точек.

Значит из верних соотношений имеем P(A)=\frac{\pi}{4}=\frac{m}{n} \Rightarrow \pi=4*\frac{m}{n}

Программируем

import random

def estimate_pi(n):
    num_point_circle = 0 #кол-во точек внутри круга
    num_point_total = n

    for i in range(n):
        x = random.uniform(0,1)
        y = random.uniform(0,1)
        distance = x**2 + y**2

        if distance <= 1: #определяем, что точка попала внутрь круга
            num_point_circle += 1

    return 4 * num_point_circle/num_point_total

n = 10000000 #общее количество точек (чем больше точек, тем лучше точность)
pi =  estimate_pi(n)

print(pi)

На этом все!

Надеюсь вам понравилась задача! Делитесь своими интересными задачками с собеседований, будем разбирать)

Связаться со мной @polozovs

© Habrahabr.ru