Ищем мелодию по фрагменту
Приветствую, уважаемые читатели Хабра! В этой статье хочу рассказать, как я искал музыкальное произведение по его отрывку.Итак, поехали! Задача передо мной стоит следующая: есть отрывок музыкального произведения, есть база музыкальных произведений, и необходимо найти, какому из имеющихся музыкальных произведений принадлежит данный отрывок.Кому интересно, читайте под харбокатом! Я решил, что для этих целей я представлю музыку как функцию частоты от времени.Для этого я сделаю следующее: «нарежу» сигнал на окна, как это проиллюстрировано на рисунке и буду использовать модификацию алгоритма скользящего окна. Модификация будет заключаться в том, что окно будет не «плавно скользить» по сигналу, а «двигаться по сигналу отрывисто», другими словами, окна будут перекрываться
В качестве окна мы возьмем так называемое «окно Хемминга».В качестве момента времени появления составляющей с той или иной частотой будем брать момент времени, соответствующий середине окна. Данная модификация позволит улучшить разрешение во временной и частотной областях: в частотной за счет сравнительно большого окна, а во временной — по причине того, что окно Хемминга имеет сравнительно узкий главных лепесток и при перемещении окна с перекрытием, мы можем достаточно точно фиксировать временные отсчеты.В каждом окне мы будем выполнять преобразование Фурье, для того, чтобы получить набор частот, которые присутствуют в данном окне.Итого для произвольной композиции мы получим следующее: На входе — зависимость амплитуды от времени: 
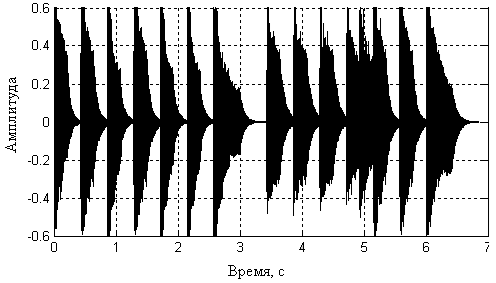А на выходе — зависимость амплитуды от частоты: 
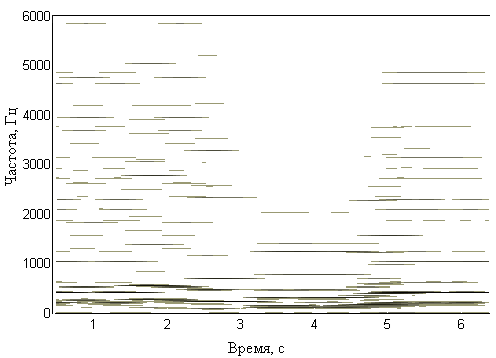На этом мы не заканчиваем.После того, как мы получили время-частотное представление, мы отфильтровываем различные помехи, и выделяем частоты, которые соответствуют нотам.Тем самым мы получаем время-нотное представление — функцию номера ноты от времени.Но тут мы сталкиваемся, с тем, что одна и та же мелодия может быть проиграна с различных нот, например (на рисунке (а) с более высокой ноты, а на рисунке (б) — с более низкой ноты): 
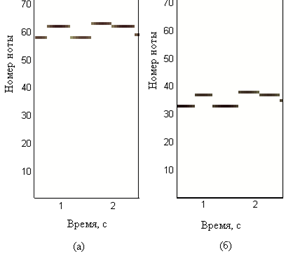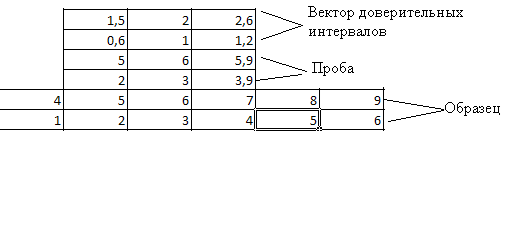
Но если мы присмотримся к картинкам, мы поймем, что картинки похожи.Отсюда появилась следующая идея: что бы идентифицировать музыкальное произведение вне зависимости от тональности, на которой оно было сыграно, следует учитывать не абсолютные значения номеров нот и времени их появления, а относительные — разности между значениями следующих и предыдущих отсчетов номеров нот и времен.Итак, мы можем получить из время-нотной функции двухстрочную матрицу, в одной строке которой будут разницы нот, а в другой строке разницы времен их появления, таким образом, мы учтем и ритм.Несмотря на то, что произведения были сыграны на разных тональностях, справедливо следующее соотношение: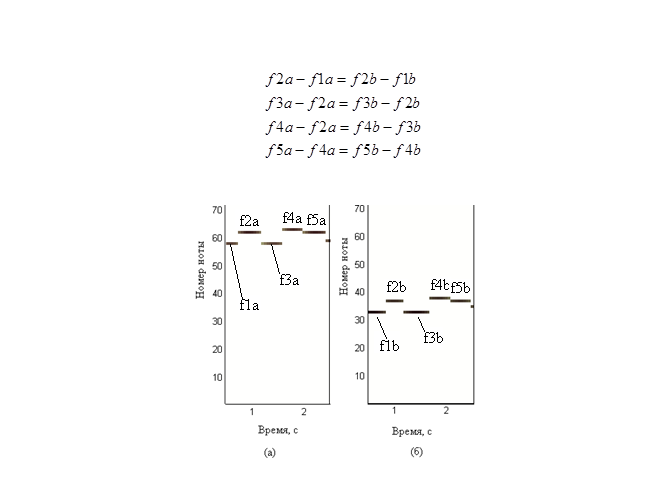 
Алгоритм идентификации заключается в следующем: высчитывается вектор доверительных интервалов — берется аудиоотпечаток сигнала, принятого за образец (в данном случае это матрица с двумя строками и некоторым количество столбцов), и вычисляется такого же размера вектор, элементы которого равны тридцати процентам от абсолютных величин соответствующих им элементов в образце;
далее аудиоотпечаток меньшего размера перемещается по аудиоотпечатку большего размера по принципу скользящего окна. При этом считаются модуль разностей соответствующих элементов, и осуществляется проверка, чтобы эта разность была не больше соответствующих элементов вектора доверительных интервалов;
если эта разность не больше, то считается число столбцов. удовлетворяющих условию;
затем это число нормируется числом столбцов в «меньшем» аудиоотпечатке;
после этого выбирается максимальная доля сходства.
И далее если доля сходтсва, в моем случае выше 75%, то я считаю, что мелодия найдена.
