Инструменты анализа временных рядов в ETNA
Меня зовут Саша, я разработчик библиотеки ETNA в Тинькофф. Расскажу про методы EDA в библиотеке ETNA, а также о том, что можно увидеть с их помощью в данных и как использовать для улучшения модели прогнозирования.
Условия задачи
Попробуем найти что-то интересное во временных рядах из соревнования Web Traffic Time Series Forecasting. Организаторы предлагают участникам спрогнозировать количество посетителей страниц Википедии, а качество прогнозов оценить по SMAPE. Поэтому в статье будем ориентироваться на эту метрику.
В предыдущих статьях наша команда рассказывала, как прогнозировать временные ряды и как использовать для этого дополнительные данные. Если бейзлайн уже построен, метрики перестали улучшаться — самое время вернуться на шаг назад и приступить к EDA.
Выбросы, пропуски и прочие неприятности
Пропуски. В условиях соревнования указано, что в данных есть пропуски. Организаторы подсказывают, что они могут возникать из-за отсутствия данных или просто из-за того, что трафик в этот день был нулевой.
Попробуем визуализировать разные варианты заполнения пропусков. Заполнение нулями выглядит не очень правдоподобно:
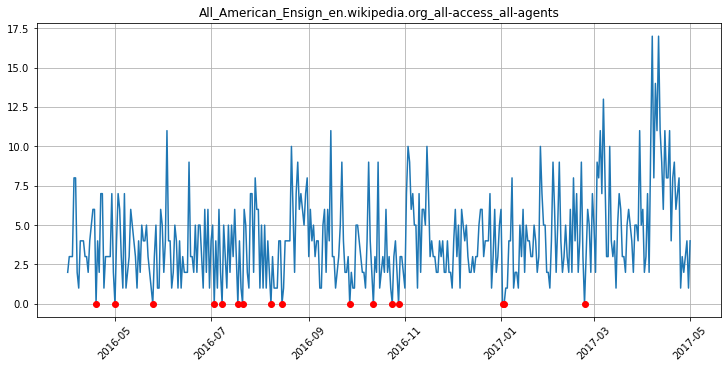Возможно, в какие-то дни действительно нулевое количество посещений, но точно определить такие дни мы не можем, поэтому заполнять все пропуски нулями — не самая правильная стратегия.
Последнее известное значение выглядит лучше, но может плохо работать, если пропуском является целый интервал:
Заполняя пропуски последним известным значением, мы предполагаем, что количество посещений в текущий день не отличается от количества посещений в предыдущий. Такое предположение — грубое, но оно позволяет избежать появления неожиданных нулей. Но если пропуском является целый интервал, заменять его на константу неправдоподобно. Хочется сохранить тренд.
Скользящее среднее последних трех дней выглядит как идеальный вариант:
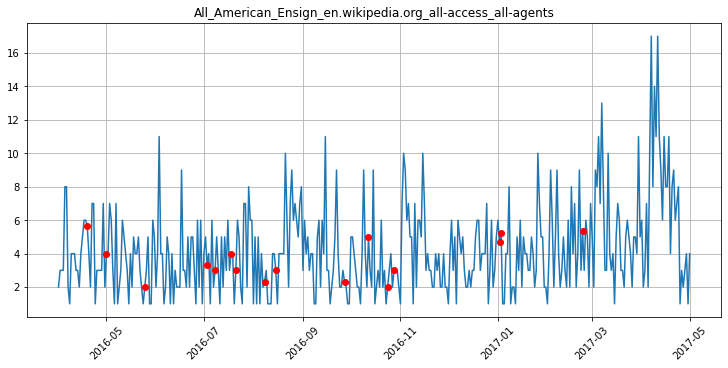Заполнение пропусков скользящим средним за последние три дня позволяет сохранять текущий тренд в количестве посещений. В предыдущей стратегии текущий тренд не учитывался, и это было ее большим недостатком.
Выбросы. Заполнили пропуски — стало понятнее. Остались выбросы и аномалии. Выбросами назовем необъяснимые пики или сдвиги уровня ряда в случайные моменты времени. Чаще всего это следствия сбоев или ошибок при выгрузке данных, и они не отражают поведения ряда.
Для обработки выбросов есть методологии на любой вкус и цвет. Например, можно добавить специальный признак-индикатор, заменить выбросы, как мы это делали с пропусками, или просто выкинуть из датасета. Попробуем второй путь.
В нашей библиотеке есть целый набор методов для детектирования выбросов. К сожалению, все методы страдают общим «недугом» — для них нужно подбирать гиперпараметры:
Визуализация выбросов, найденных методом на основе оценки плотности: на графике отмечены точки, которые классифицированы как аномалии.
Параметры можно подбирать и в интерактивном режиме, пример — в ноутбуке по ссылке выше.
Попробуем спрогнозировать наш ряд на шесть недель вперед, оставив выбросы на месте, а затем «исправив» их, как договорились выше:
Сравним качество прогноза по метрике SMAPE с выбросами и без:
SMAPE | |
До удаления выбросов | 33.84 |
После «исправления» выбросов | 28.88 |
Обработка выбросов улучшила нашу метрику примерно на 15%! Выглядит как убедительный довод в пользу того, что обработка выбросов — это определенно важная часть пайплайна прогнозирования.
Аномалии. Появление выбросов в ряде невозможно предсказать из-за их случайной природы, но в рядах есть и другие аномальные участки. Некоторые из них на первый взгляд ничем не отличаются от выбросов — например, пики в праздничные дни. Такое поведение ряда ожидаемо, и можно попробовать научить модель его предсказывать. Разберемся, как это делать, на примере ряда, связанного с сериалом Black Sails.
Количество посещений страницы сериала в день. Пики соответствуют выходу новых сезонов.
Аномальное поведение в начале года — выход очередного сезона. Нам известно об успехах первого сезона сериала в 2016 году, можем оценить нагрузку на сервера в период выхода новых серий в 2017 году.
Например, популярная модель Prophet умеет из коробки учитывать эффект таких событий, но для этого нужно подобрать параметры событий:
Визуализация границ влияния выхода нового сезона на посещаемость страницы. В этих границах значения ряда существенно отличаются от среднего, эту информацию мы хотим добавить в модель.
Дата выхода сериала известна, окно зависимости от выхода сезона мы определили, можно прогнозировать 2017 год. Попробуем сделать прогноз тремя способами — с дефолтными параметрами, с включенной годовой сезонностью и с включенной годовой сезонностью и учетом выхода сезона:
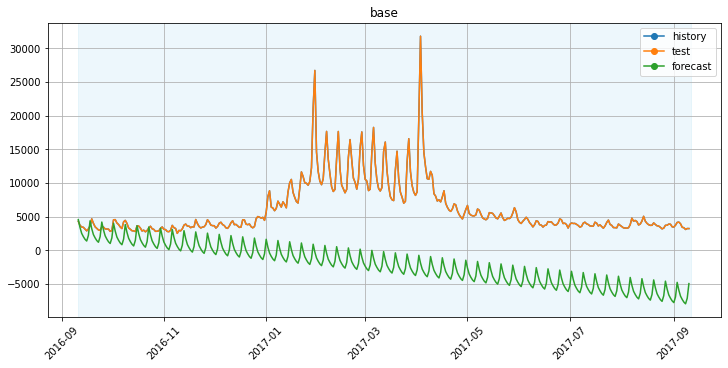Прогноз модели Prophet с дефолтными параметрами: модель сумела уловить недельную сезонность, но учесть выход нового сезона в прогнозе не получилось.
Прогноз модели Prophet с включенной годовой сезонностью. Годовая сезонность позволила уловить пик, связанный с выходом нового сезона, поскольку выход нового сезона — ежегодное событие. Но уловить увеличение дисперсии внутри пика не удалось.
Прогноз модели Prophet c включенной годовой сезонностью и учетом выхода сезона. На графике видно, что информация о выходе нового сезона улучшила качество прогноза.
Мы попробовали три конфигурации модели Prophet, сравним метрику SMAPE:
SMAPE | |
Бейзлайн | 171.94 |
Годовая сезонность | 41.27 |
Годовая сезонность + событие | 20.65 |
Без учета эффекта выхода нового сезона в модели предсказать ничего особо не получается. Годовая сезонность улучшила картину, но информация о новом сезоне улучшила метрику еще в два раза.
Тренд и сезонность
Более глобальные свойства временных рядов — тренд и сезонность.
Сезонность — периодические колебания значений ряда.
Включение в модель годовой сезонности улучшило качество в предыдущем примере, но есть подозрение, что в данных могут присутствовать и более мелкие сезонности.
Для определения сезонности используем инструменты из нашей библиотеки. Все начинающие специалисты по временным рядам сталкивались с графиком автокорреляции. Его и используем, смотрим на соседние значимые пики, и видим недельную сезонность:
График автокорреляции.
Посмотрим на более экзотичную картину — периодограмму. На ней изображены амплитуды компонент ряда Фурье с периодом в год:
Периодограмма временного ряда. Видим пик в точке 52, характерный для недельной сезонности (52 раза в год), а также пики рядом с 1 и 2, показывающие годовую и полугодовую сезонность.
Попробуем другую модель, Catboost, и смоделируем недельную сезонность с помощью метки дня недели, а более длинные сезонности — с помощью признаков Фурье:
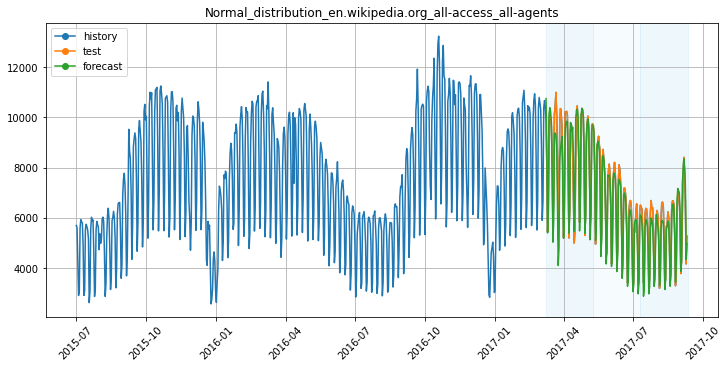Прогноз модели Catboost на сезонных признаках.
Видим, что модель успешно уловила годовую и недельную сезонность, можем двигаться дальше и переходить к тренду.
Тренд — глобальная тенденция изменения показателей временного ряда.
В нашей библиотеке реализовано несколько методов моделирования тренда, их также можно визуализировать и, конечно, добавить в пайплайн:
Визуализация линейного и кусочно-линейного тренда. На графике видно, что тренд у ряда несколько раз менялся, поэтому моделировать его лучше кусочно-линейной функцией.
Визуализация подсказывает нам, что тренд у ряда лучше моделировать кусочно-линейной функцией. Давайте проверим, действительно ли это так, на практике. Попробуем спрогнозировать ряд тремя способами: без моделирования тренда, моделируя тренд линейной функцией и моделируя тренд кусочно-линейной функцией:
Прогноз модели Catboost без моделирования тренда. На графике видно, что прогнозы слегка завышены.
Прогноз модели Catboost с моделированием тренда линейной функцией. Теперь прогнозы получились немного заниженными, как можно было ожидать, исходя из визуализации линейного тренда.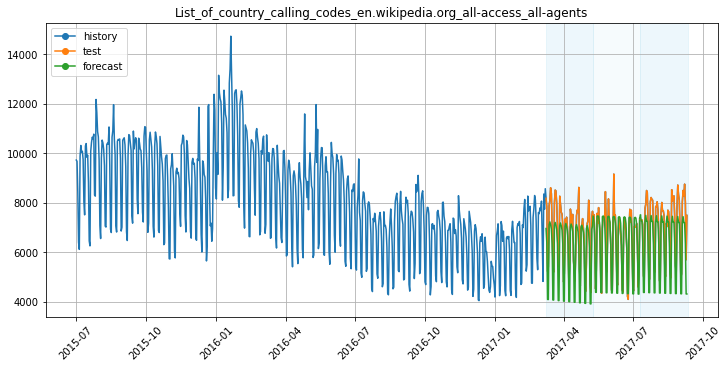
Прогноз модели Catboost с моделированием тренда кусочно-линейной функцией. Прогнозы получились не идеальными, однако уровень ряда уже больше похож на истинный.
Сравним качество прогноза для рассмотренных методов по метрике SMAPE:
SMAPE | |
Без тренда | 16.77 |
Линейный тренд | 19.10 |
Кусочно-линейный тренд | 10.73 |
Использование кусочно-линейной функции для моделирования тренда улучшает качество прогноза на 37% относительно пайплайна прогнозирования без моделирования тренда. При этом моделирование тренда линейной функцией даже ухудшает качество.
Анализ качества модели
На протяжении статьи я показал различные особенности в отдельных сегментах, но стоит помнить, что датасет состоит из 145 тысяч рядов. Не будем травмировать наши вычислительные мощности и попробуем спрогнозировать случайные 100.
Представим, что этап борьбы с данными позади, есть пайплайн и нужно оценить, насколько он хорош. Запустим бэктест и визуализируем результаты, как мы уже делали это ранее. Хотя разглядывать картинки для 100 сегментов — так себе идея. Предлагаю посмотреть, как распределена целевая метрика:
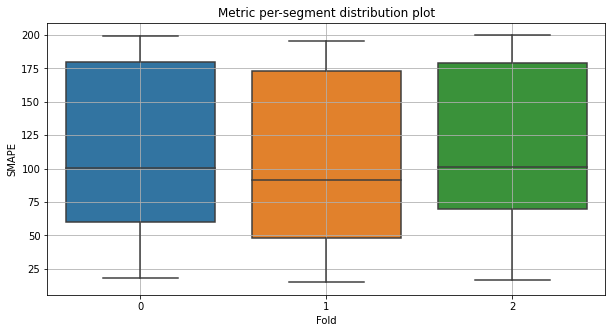Распределение метрики SMAPE в разрезе фолдов. На разных фолдах метрика распределена похожим образом, значит, модель стабильна. На графике видно, что у распределения метрики широкий разброс, значит, качество прогнозирования варьируется от сегмента к сегменту.
Неплохой разброс. Посмотрим, какие сегменты мы прогнозируем лучше и хуже всего:
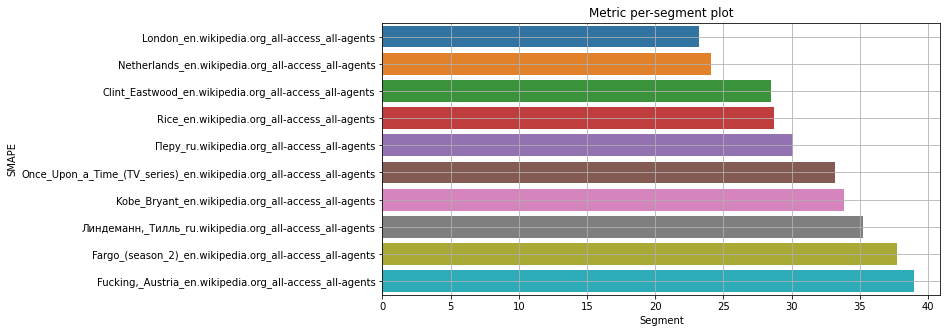Ранжирование от лучшего к худшему сегменту по качеству прогнозирования помогает отобрать сегменты с высоким качеством прогнозирования.
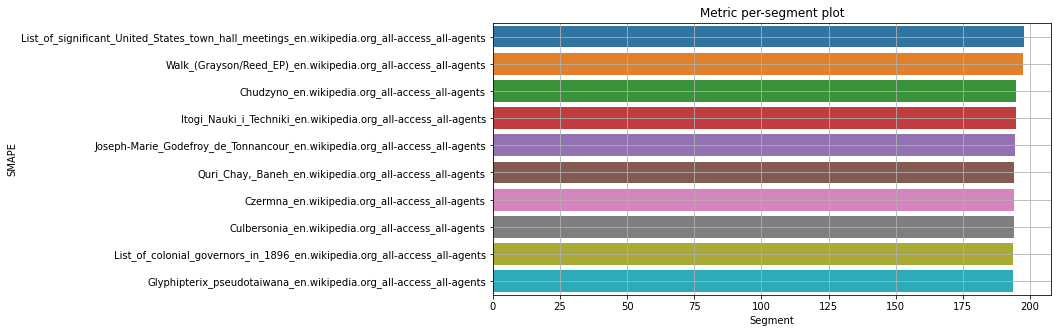10 худших сегментов по качеству прогнозирования нужно выявить для того, чтобы проанализировать их отдельно.
Посмотрим на важность признаков:
Диаграмма важности признаков: видим, что для модели самыми важными признаками оказались признаки Фурье.
Вместо итогов
В статье мы рассмотрели различные особенности данных, которые могут существенно влиять на качество прогнозирования. В их числе могут выступать аномальное поведение, выбросы, сезонность, тренд и многое другое. Обнаруживать эти особенности нам помогают методы EDA, при этом большую часть интересных находок из этих методов можно легко добавить в пайплайн прогнозирования и задешево улучшить качество нашей модели. Надеюсь, мне удалось убедить вас, что EDA — это полезный шаг при построении пайплайна.
Если статья вам понравилась, не стесняйтесь ставить нам звездочки на GitHub. Для тех, кто хочет самостоятельно покопаться в данных и попробовать все наши методы EDA в деле, прилагаю код для загрузки данных.
