Имитационная модель процесса обработки материала резанием на токарном станке с ЧПУ
Введение
Методология разработки имитационных моделей и симуляторов по различным техническим дисциплинам в основном ориентирована на снижение уровня абстракции учебного материала. Наряду с теоретическим учебным материалом наглядное имитационное моделирование того или иного технологического процесса или операции позволяет учащемуся в более полной мере освоить преподаваемый материал с максимальным приближением к естественным условиям. При этом имитационные модели и симуляторы могут рассматриваться только как вспомогательный инструмент учебного процесса. Основное назначение данной категории образовательных ресурсов — базовое (начальное) ознакомление с принципами работы сложных технических объектов в условиях отсутствия возможности использования реального промышленного оборудования, либо в целях предварительного повышения компетенции учащегося перед прохождением производственной практики.
Особую актуальность представляет методология совмещения образовательных задач с инженерно-прикладными задачами в едином инструментарии, отвечающем современному уровню развития технологий и промышленности в целом. Здесь идёт речь о комплексной реализации функций автоматизированного проектирования (CAD/CAM) и принципов имитационно-численного моделирования технологических процессов.
Основная тенденция внедрения имитационных учебных моделей в практику инженерного образования заключается в достижении максимальной интерактивности. Необходимым условием здесь является возможность выполнения «ошибочных» действий учащимся и адекватное реагирование имитационной модели на эти действия с целью достижения требуемого уровня понимания учебного материала учащимся. Чем выше степень свободы моделируемого объекта (устройства или станка), тем больший эффект реального взаимодействия достигается в процессе обучения.
Цель и задачи проекта
Целью представленного проекта является разработка учебно-методического программного продукта (имитационной модели или симулятора), предназначенного для базового ознакомления начинающих специалистов машиностроительного профиля с принципами программирования операций токарной обработки деталей с использованием стандартного G/M-кода.
Области применения программного продукта в первую очередь охватывают образовательный процесс с использованием вычислительной техники в форме лабораторных занятий студентов в компьютерных классах, дистанционного обучения, а также демонстрационной поддержки лекционного материала по группе направлений подготовки и специальностей (ОКСО) «Металлургия, машиностроение и материалообработка». Гибкая функциональность и мобильность программного продукта также позволяют использовать его в качестве прикладного инструмента для верификации и предварительного тестирования управляющих программ операций токарной обработки материалов на станках с числовым программным управлением (ЧПУ) с применением программного кода Fanuc (система кодов А).
Функциональные возможности симулятора должны обеспечивать выполнение следующих задач:
- составление текстов управляющих программ операций токарной обработки в формате стандартного G/M кода и проверку управляющих программ на синтаксические и технологические ошибки;
- воспроизведение на экране вычислительного устройства трёхмерных графических моделей основных узлов имитируемого оборудования, технологической оснастки и металлорежущего инструмента с целью учебной имитации процесса токарной обработки материала;
- трехмерную визуализацию процесса формообразования детали при токарной обработке по составленным управляющим программам;
- визуализацию траекторий перемещения режущего инструмента в рабочей плоскости станка;
- осуществление интерактивного взаимодействия пользователя с имитационной моделью оборудования.
Техническим преимуществом разрабатываемого симулятора является относительно низкая ресурсоёмкость и мультиплатформенная поддержка, позволяющие использовать данный программный продукт на различных вычислительных устройствах, включая интерактивные доски, смартфоны, планшетные и настольные компьютеры, что, в свою очередь, повышает гибкость и мобильность учебного процесса, соответствуя современному уровню информатизации образования.
Объект моделирования
В основу трёхмерной имитационной модели заложен токарный станок ТС1625ФЗ производства Тверского станкостроительного завода АО «СтанкоМашКомплекс» с горизонтальной станиной и классической компоновкой узлов, оснащённый системой ЧПУ, восьмипозиционной револьверной головкой, трёхкулачковым токарным патроном, задней бабкой, системой подачи смазочно-охлаждающей жидкости и другими узлами. Обработка материала выполняется по двум координатам в горизонтальной плоскости станка. Основные технические характеристики прототипа оборудования представлены в таблице 1.

В симуляторе моделируется комплект режущего инструмента (сборные токарные резцы и свёрла), включающий 185 наименований. Типы используемых сменных режущих пластин токарных резцов представлены в таблице 2.
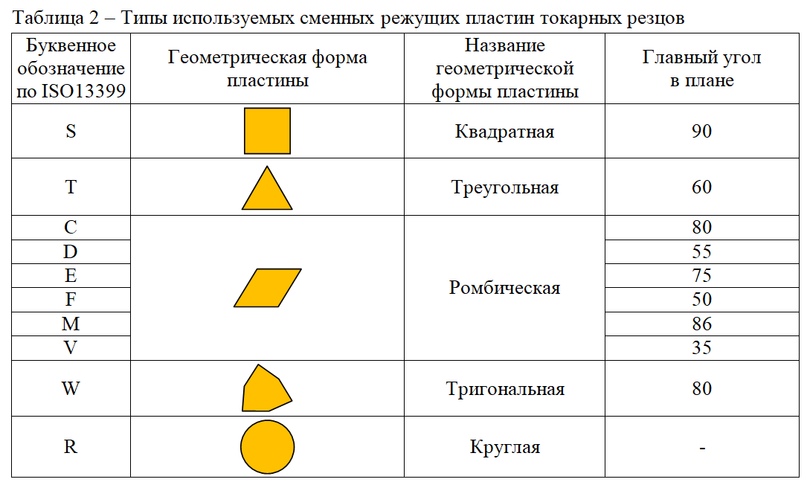
Также в модели используются резцы со специальными резьбонарезными пластинами и свёрла. На рисунке 1 представлена геометрическая модель сборного токарного резца.
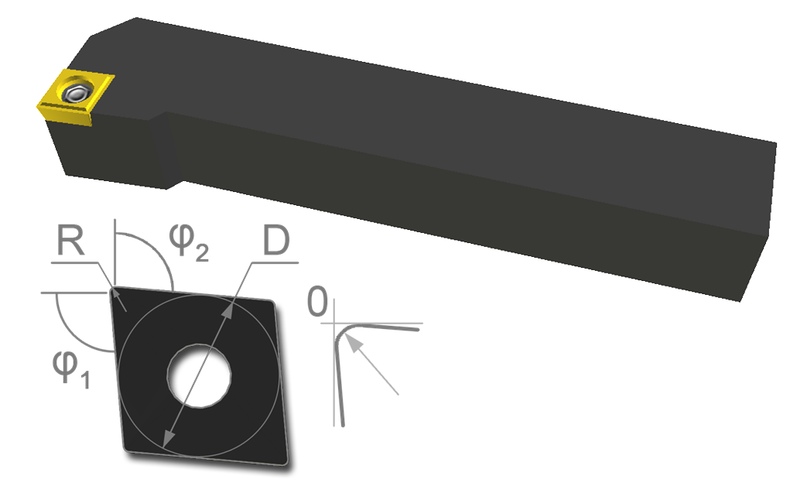
Рисунок 1 — Геометрическая модель сборного токарного резца и обозначение основных характеристик сменной режущей пластины: главного угла в плане φ1, вспомогательного угла в плане φ2, диаметра вписанной окружности D, радиуса скругления при вершине R
Краткое описание метода геометрического моделирования формообразования детали при токарной обработке
В рассматриваемом проекте применяется упрощённая модель формообразования обрабатываемой детали, основанная на допущении о постоянстве осевой симметрии детали на протяжении всего процесса токарной обработки [1, 2]. Данная модель исключает возможность построения винтовых поверхностей, а резьбовые элементы деталей изображаются условно — участками концентрической ребристости. Основные вычисления по данной методике формализованы геометрической задачей пересечения двух плоских замкнутых контуров в рабочей плоскости станка — контура обрабатываемой детали и контура режущего инструмента. На основе формообразующего контура, представляющего собой логическую разность при пересечении двух исходных контуров, образуется трёхмерная поверхность моделируемой детали путём равномерного поворота формообразующего контура вокруг главной оси станка (оси вращения обрабатываемой детали). Применяемый метод позволяет моделировать формообразование детали типа тела вращения в реальном времени при относительно низких вычислительных затратах.
Первоначальным этапом алгоритма является формирование множества точек Wi контура обрабатываемой детали (рис. 2.а). В исходном состоянии (до начала процесса обработки) контур детали включает четыре точки, при этом продольное сечение детали представлено прямоугольником. В последующих итерациях алгоритма исходным контуром детали является ранее рассчитанный формообразующий контур. Контур описывается против часовой стрелки.
На втором этапе алгоритма формируется контур режущей пластины токарного резца с учётом её геометрических характеристик — габаритных размеров, главного угла в плане и радиуса скругления при вершине. Контур режущей пластины описывается точками Cj в противоположном направлении по отношению к контуру детали (по часовой стрелке).
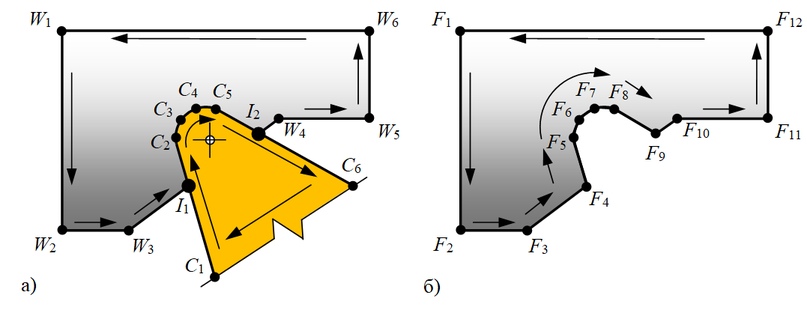
Рисунок 2 — К задаче расчёта формообразующего контура обрабатываемой детали:
пересечение исходных контуров детали и режущей пластины (а); получение формообразующего контура детали как логической разности исходных контуров (б)
Третий этап алгоритма заключается в определении множества точек пересечения Ik исходных контуров. При этом найденные точки пересечения индексируются в соответствии с тем, насколько ближе они лежат к начальной точке контура детали, и включаются в обобщённое множество точек обоих контуров в порядке индексации. Определение координат точек пересечения осуществляется для двух отрезков, принадлежащих двум разным контурам (рис. 3).
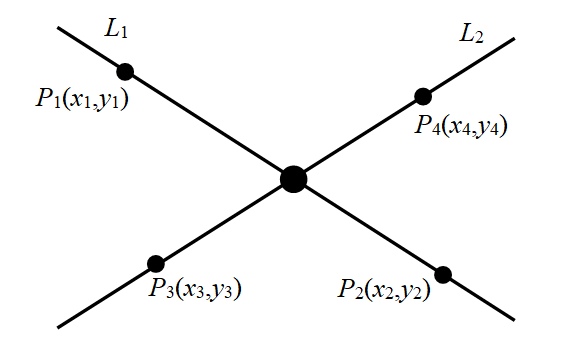
Рисунок 3 — К определению координат точки пересечения двух отрезков
Для отрезков P1–P2 и P3–P4, принадлежащих двум пересекающимся прямым L1 и L2, следует:
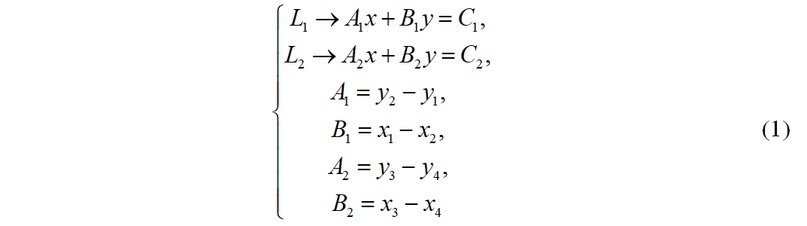
Координаты x, y точки пересечения прямых L1 и L2 определяются матричным уравнением:

следовательно:

Точки обобщённого множества, принадлежащие контуру режущей пластины, за пределами интервалов между точками пересечения, исключаются из обобщённого множества точек обоих контуров. Таким образом, формируется окончательное множество точек Fn, описывающих формообразующий контур детали (рис. 2.б). Полученный контур описывается в том же направлении, что и исходный контур детали.
Рассмотренный алгоритм представляет собой упрощенный вариант алгоритма отсечения Вейлера–Азертона [3]. Ряд упрощений алгоритма обусловлен геометрическими особенностями решаемой задачи, а именно: постоянным условием выпуклости контура режущей пластины, условиями обнаружения столкновений нерабочих элементов резца (державки) с обрабатываемой деталью, условием исключения полностью отсекаемой части детали из вычислительного процесса при моделировании операции отрезки и др.
В силу того, что моделирование формообразования детали осуществляется в процессе перемещения режущего инструмента, на каждой итерации алгоритма происходит дискретное изменение координат точек контура режущей пластины относительно контура обрабатываемой детали. Шаг дискретности в данном случае обусловлен заданным параметром движения режущего инструмента (величиной рабочей подачи) и временем итерации цикла симуляции. В данном случае шаг дискретности перемещения инструмента (δ) может превышать линейные размеры области перекрытия контуров режущей пластины и обрабатываемой детали (рис. 4.а), что приводит к появлению артефактов («непрорезанных» участков) формообразующего контура детали (рис. 4.б).
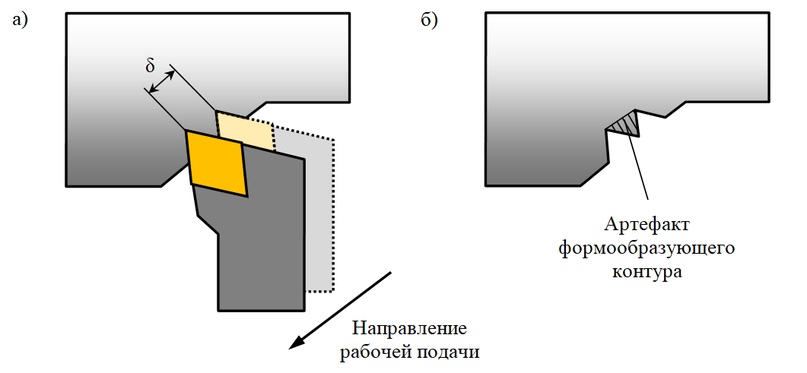
Рисунок 4 — Проблема дискретности вычисления пересечений контуров
Одним из решений описанной проблемы является метод Джарвиса, заключающийся в построении минимальной выпуклой оболочки вокруг множества вершин контуров режущей пластины в текущем и предшествующем дискретных состояниях (рис. 5).

Рисунок 5 — Построение минимальной выпуклой оболочки вокруг контуров режущей пластины в двух последовательных дискретных состояниях
В данном случае осуществляется расчет пересечения контура обрабатываемой детали с контуром минимальной выпуклой оболочки, обеспечивающей требуемую область перекрытия в промежутках между дискретными состояниями режущего инструмента. При построении минимальной выпуклой оболочки особенно важным является условие неизменности направления обхода её контура. Минимальная выпуклая оболочка может охватывать несколько дискретных состояний режущей пластины при условии, что направление рабочей подачи резца не меняется в данных состояниях (резец перемещается по прямой траектории).
В рассматриваемом проекте применяется альтернативный метод устранения артефактов формообразующего контура, основанный на алгоритме генерализации Рамера-Дугласа-Пекера [4, 5], широко применяемом в задачах топографии и картографии. Основной целью рекурсивной процедуры генерализации является сокращение числа вершин ломаной линии на основе заданного порогового значения расстояния между вершинами. Начальным условием работы алгоритма является выбор наиболее удаленной точки по отношению к начальной точке ломаной линии контура. В последующих итерациях алгоритма определяются расстояния между промежуточными точками ломаной линии и сравниваются с пороговым значением. Соединение точек в аппроксимирующую полилинию осуществляется при условии превышения расстояния между ними над заданным пороговым значением (рис. 6).
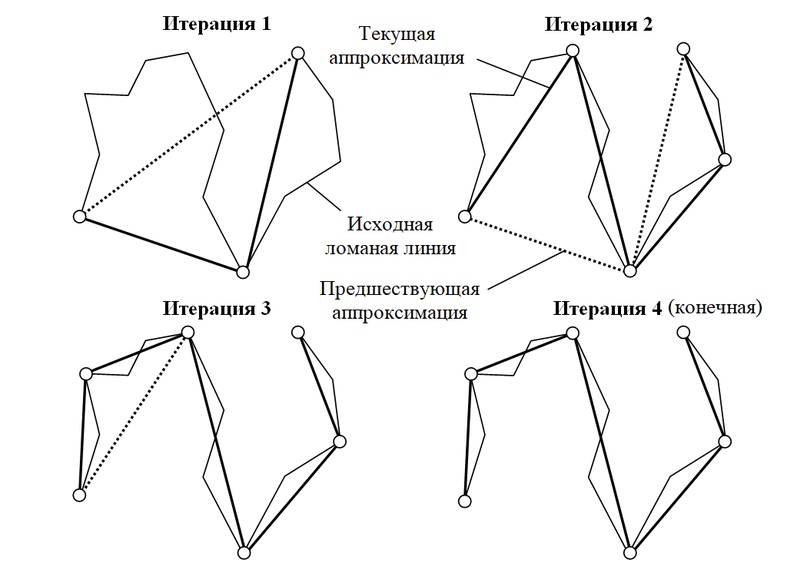
Рисунок 6 — Итерации алгоритма генерализации Рамера-Дугласа-Пекера на примере произвольной ломаной линии
Технически процедура аппроксимации формообразующего контура детали объединена с начальным этапом общего алгоритма моделирования, на котором происходит формирование множества вершин исходного контура обрабатываемой детали.
Формирование трёхмерной поверхности моделируемой детали осуществляется путём расчёта координат точек в окружностях поперечных сечений детали по длине формообразующего контура с последующим объединением данных точек в треугольные фасеты (между сечениями). Длина радиус-вектора Ri каждой точки формообразующего контура вычисляется как расстояние от данной точки до главной оси станка (рис. 7).
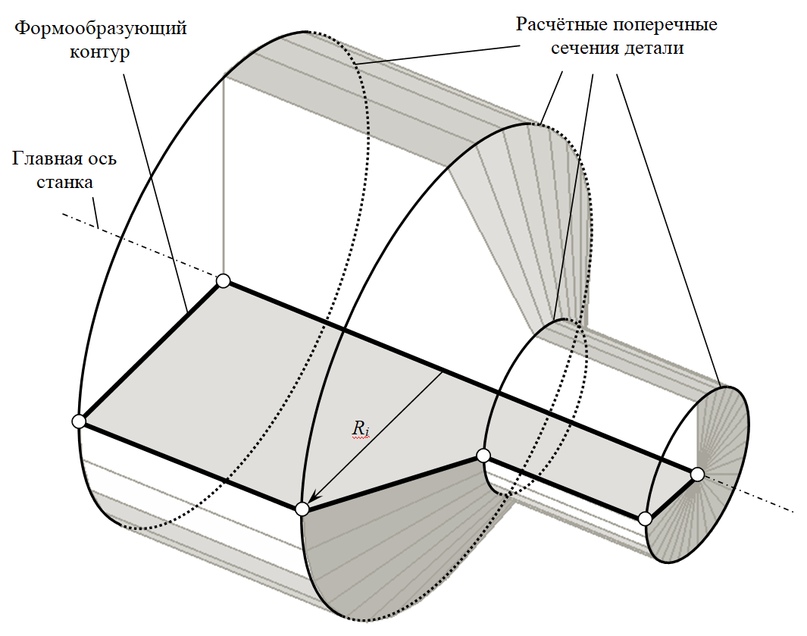
Рисунок 7 — Полигональная модель детали типа тела вращения в разрезе (разбиение полигонов на треугольные фасеты не показано)
Порядок обхода вершин при сборке трёхмерного каркаса строго определён. Каждый полигон трёхмерной поверхности разбивается на 2 треугольных фасета, объединяющих 4 вершины (рис. 8). Радиальная гладкость образуемой трёхмерной поверхности зависит от заданного количества сегментов (секторов круга) в сечении моделируемой детали. В процедуре сборки трёхмерного каркаса также рассчитываются векторы нормалей в каждой вершине (рис. 9) и текстурные координаты UV. По рассчитанным текстурным координатам поверхность детали прорисовывается с наложенным изображением текстуры металла, что в свою очередь повышает реалистичность восприятия моделируемого процесса.
Таким образом, окончательная трёхмерная модель обрабатываемой детали позволяет визуализировать результаты удаления материала резцом в динамике реального времени с требуемой степенью реалистичности.

Рисунок 8 — Фасеточный каркас трёхмерной модели обрабатываемой детали, вписанный в габаритный цилиндр исходной заготовки

Рисунок 9 — Векторы нормалей в вершинах фасеточной модели обрабатываемой детали
Принципы имитационного моделирования числового программного управления процессом токарной обработки материала
Перечень основных функций программного управления станком
В качестве лингвистической основы для программирования основных технологических операций при токарной обработке материала выбраны G-M коды системы числового программного управления Fanuc:
G00/G01 — линейная интерполяция на ускоренной/рабочей подаче;
G02/G03 — круговая интерполяция по/против часовой стрелки;
G04 — выдержка времени;
G20/G21 — ввод данных в дюймах/миллиметрах;
G32/G34 — нарезание резьбы с постоянным/переменным шагом за один проход;
G50 — установка максимальной частоты вращения шпинделя;
G53–G59 — переключение между рабочими системами координат №1–6;
G70–G76 — основные токарные циклы;
G80–G83 — циклы обработки отверстий;
G90 — цикл основной токарной обработки наружного/внутреннего диаметра;
G92 — цикл нарезания резьбы с постоянным шагом;
G94 — цикл основного наружного/внутреннего торцевого точения;
G96/G97 — постоянная скорость резания/вращения шпинделя;
G98/G99 — скорость подачи [мм/мин]/скорость подачи [мм/об];
M00/M01 — программный останов с подтверждением;
M02/M30 — завершение управляющей программы;
M03/M04 — запуск вращения шпинделя по/против часовой стрелки;
M05 — остановка вращения шпинделя;
M07–M09 — включение/выключение подачи СОЖ;
M38/M39 — открытие/закрытие автоматических дверей;
M97–M99 — вызов и завершение внутренних/внешних подпрограмм.
Структура и формат кода управляющих программ
Код управляющей программы представляется в виде последовательности строк (кадров). Симулятор позволяет разрабатывать и выполнять управляющие программы объёмом до 999 кадров (с учетом первой нередактируемой строки, содержащей номер управляющей программы). Каждый кадр состоит из последовательности слов, представляющих собой сочетание буквенного адреса и числового параметра. Между адресом и параметром не допускаются пробелы. Набор текста управляющей программы осуществляется буквенными латинскими и цифровыми символами с использованием моноширинного шрифта. Допускается использование некоторых специальных символов. Любая группа символов, не подлежащая синтаксическому анализу, должна быть заключена в круглые скобки либо записана после символов »;» или »/». Данная информация считается комментарием к коду и не анализируется в процессе симуляции. Адреса подготовительных (G) и вспомогательных (M) функций программируются с целочисленными параметрами, определяющими номера данных функций. Числовые параметры позиционирования (после адресов X, Z, U, W, I, K, R и др.) могут задаваться дробными или целыми значениями. Здесь допускается использование знака «минус».
После запуска процесса симуляции производится автоматическая проверка кода управляющей программы на соответствие формату. В случае обнаружения ошибок на экран выводятся соответствующие сообщения.
Краткое описание алгоритма парсинга управляющих программ
Синтаксический анализ (парсинг) кода управляющей программы (УП) и симуляция его выполнения осуществляются по стандартному алгоритму [6], блок-схема которого представлена на рисунке 10.
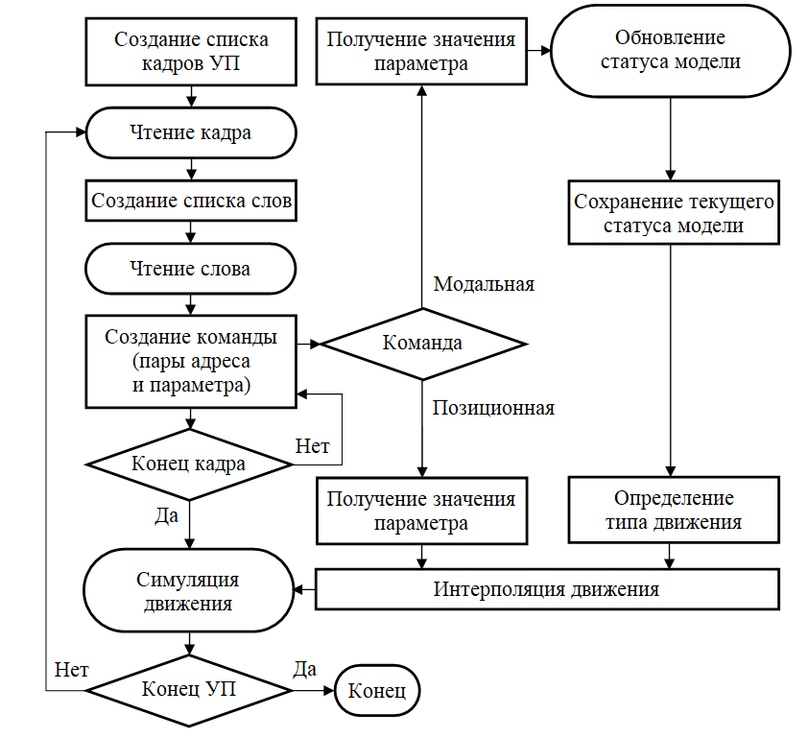
Рисунок 10 — Блок-схема алгоритма парсинга УП
В соответствии с приведённой на рисунке 10 блок-схемой парсинг управляющей программы начинается с формирования списка кадров. Для каждого кадра формируется список слов. Слово представляет собой структуру данных — команду, включающую буквенный адрес и числовой параметр. Команды условно классифицируются как модальные и позиционные.
Модальные команды изменяют статус имитационной модели станка, и определяют её текущее состояние — режим перемещения инструмента (перемещение на ускоренной или рабочей подаче, тип интерполяции), режим вращения шпинделя, положение автоматических дверей, состояние системы охлаждения и т.д. В свою очередь, позиционные команды определяют непосредственно параметры перемещений — координаты конечных точек, параметры дуг при круговой интерполяции и т.д.
По полученным параметрам движения осуществляется интерполяция координат режущего инструмента, углов поворота вращающихся элементов станка, положения автоматических дверей и др. Таким образом, происходит покадровая симуляция управляющей программы. При достижении последнего кадра процесс симуляции завершается.
Реализация управления перемещениями токарного инструмента
По аналогии с реальной системой ЧПУ перемещение режущего инструмента программируется методами линейной и круговой интерполяции. Линейная интерполяция является основным видом движения при обработке на токарном станке с ЧПУ. При линейной интерполяции инструмент перемещается по прямой траектории с известными координатами её начала и конца (рис. 11).
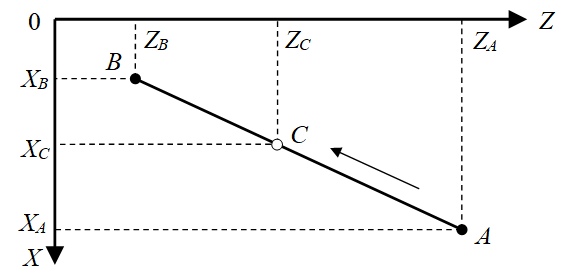
Рисунок 11 — Траектория движения инструмента при линейной интерполяции
При движении расчётной точки C из точки A в точку B по прямолинейному участку с постоянной скоростью подачи обе координаты интерполируются линейно по времени. Обозначив время начала перемещения как tA, а конечное время — tB, текущие координаты точки C, соответствующие текущему моменту времени tC, можно определить по формулам линейной интерполяции:
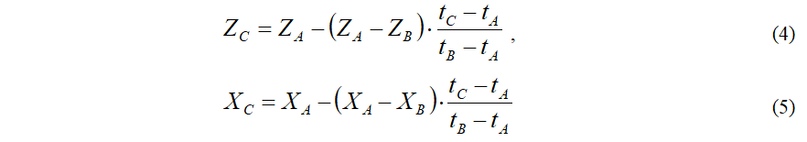
Конечное время перемещения определяется как:

где tS — время, затраченное на прямолинейное перемещение при постоянной скорости подачи F (мм/мин):

Линейная интерполяция на ускоренной подаче программируется модальной функцией G00 (данная функция активна в исходном состоянии системы ЧПУ). Линейная интерполяция на рабочей подаче программируется модальной функцией G01. После данных функций задаются координаты конечной точки прямолинейного участка пути. За исходную точку всегда принимается текущее положение инструмента. Заданная скорость рабочей подачи при ускоренном перемещении игнорируется. Координаты конечной точки могут задаваться в абсолютных значениях (X, Z), то есть относительно нуля рабочей системы координат, либо в относительных (инкрементальных) значениях (U, W), то есть относительно исходной точки прямолинейной траектории. Если одна из координат опущена, перемещение по соответствующей ей оси не осуществляется.
Круговая интерполяция применяется для вытачивания криволинейных поверхностей, форма которых описывается дугой окружности определённого радиуса. Применяются два метода программирования дуги. Первый метод заключается в задании координат центра дуги и конечной точки, при этом радиус дуги вычисляется автоматически. Второй метод предполагает указание радиуса дуги и координат конечной точки, при этом координаты центра дуги вычисляются автоматически. Круговая интерполяция по часовой стрелке задается с помощью функции G02, а круговая интерполяция против часовой стрелки — функцией G03, соответственно.
Рассмотрим один из случаев круговой интерполяции против часовой стрелки с указанием центра дуги (рис. 12.а). При движении расчетной точки C из точки A в точку B по дуге с постоянной скоростью подачи обе координаты также можно интерполировать по времени. Траектория движения задается положением конечной точки B и положением центра дуги O в инкрементальных координатах (i, k) относительно исходной точки A.
Угловое положение радиус-векторов OA, OB и OC описывается тригонометрическими углами φA, φB и φC, соответственно.
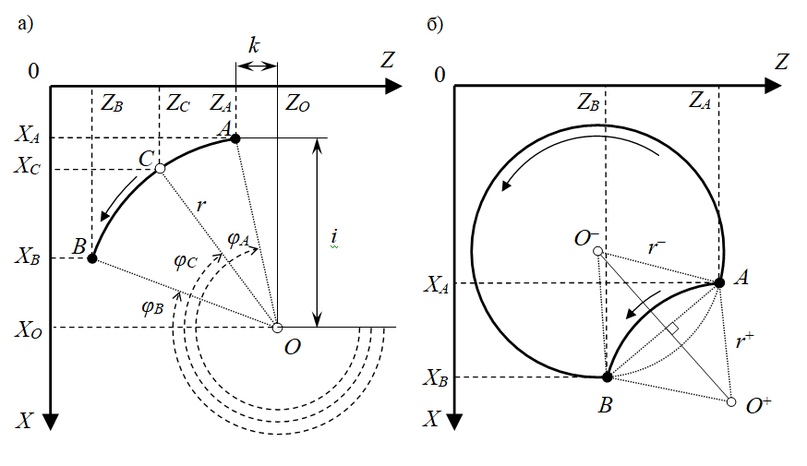
Рисунок 12 — Траектория движения инструмента при круговой интерполяции против часовой стрелки с заданием: центра дуги (а); радиуса окружности дуги (б)
Обозначив время начала перемещения как tA, а конечное время — tB, угол φC, соответствующий текущему моменту времени tC, можно определить по формуле линейной интерполяции:

где φA, φB — тригонометрические углы радиус-векторов начальной и конечной точек дуги:

Примечание: при расчёте тригонометрических углов крайних точек дуги необходимо учитывать ситуации, при которых функция арктангенса принимает сингулярные значения.
Декартовые координаты точки C определяются как:

где

Конечное время перемещения определяется по выражению (6). При этом время tS, затраченное на перемещение по дуге при постоянной скорости подачи F (мм/мин), можно определить, используя выражение длины дуги:
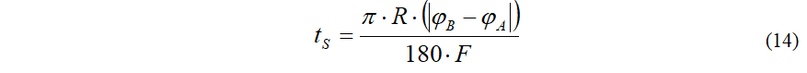
Инкрементальные координаты центра дуги программируются адресами I и K в направлениях осей X и Z, соответственно. При программировании круговой интерполяции с указанием центра дуги необходимо, чтобы радиус-векторы начальной и конечной точек дуги имели одинаковую длину.
Круговая интерполяция всегда выполняется на рабочей подаче.
Второй метод программирования дуги — указание радиуса окружности дуги. При этом допускается два случая задания радиуса — с положительным или отрицательным значением. Если значение радиуса положительно, угол дуги составляет менее 180 градусов. В противном случае угол дуги составляет более 180 градусов (рис. 12.б). При задании дуги радиусом система ЧПУ автоматически определяет положение центра дуги (O+ или O– в зависимости от знака радиуса). В данном методе задания дуги должно соблюдаться условие: модуль радиуса не может быть меньше половины длины хорды (AB) дуги.
На рисунке 13 показан пример образования криволинейной поверхности при программировании круговой интерполяции против часовой стрелки.
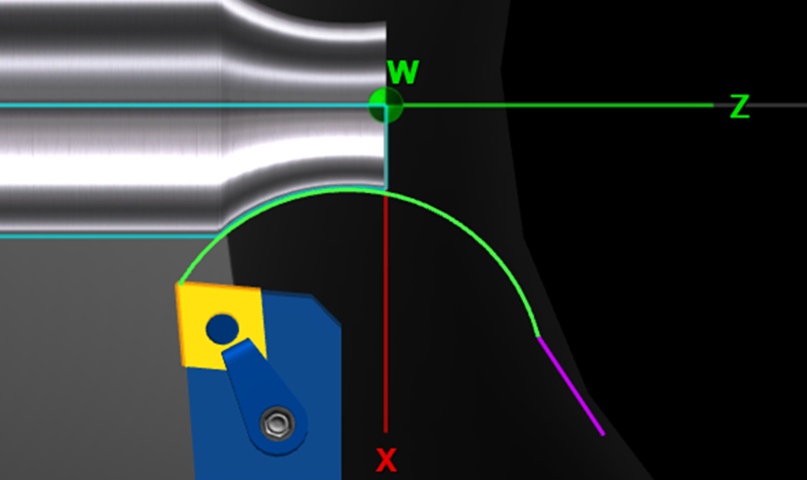
Рисунок 13 — Образование криволинейной поверхности при программировании круговой интерполяции против часовой стрелки
Реализация функций работы с системами координат
Представленная имитационная модель включает несколько систем координат (рис. 14). Главной и неизменной системой координат является система координат станка с началом, соответствующим точке машинного нуля M, геометрически совпадающей с точкой пересечения торцевой плоскости шпинделя и оси его вращения.
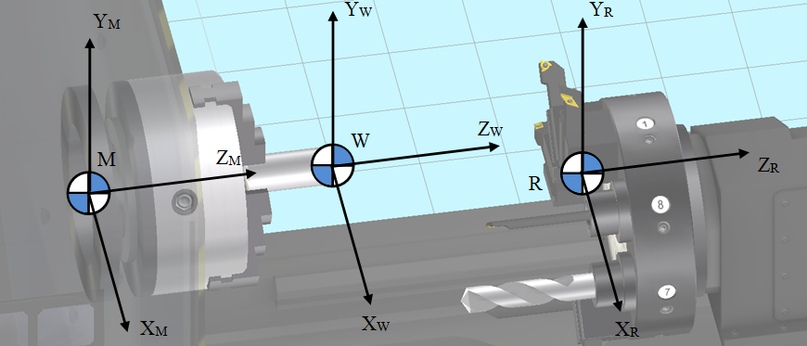
Рисунок 14 — Основные системы координат имитационной модели
Второй немаловажной системой координат является референтная система координат с началом, соответствующим референтной точке R или точке смены инструмента. В данной системе координат рассчитываются основные перемещения подвижных узлов станка, и определяются столкновения инструмента с конструктивными элементами станка при моделировании возможных аварийных ситуаций.
Программирование процесса токарной обработки осуществляется в рабочей системе координат. В симуляторе предусмотрено 6 независимых рабочих систем координат с нулевыми точками W1–6. Начальные настройки положения данных нулей задаются пользователем в параметрах имитационной модели и обозначаются как нулевые корректоры.
Направления осей в каждой системе координат одинаковы. Продольная ось Z всегда направлена от токарного патрона в сторону задней бабки станка. Поперечная ось X (или ось диаметров) направлена в сторону суппорта (на себя при фронтальном ракурсе на станок). Ось Y является нормалью рабочей плоскости ZX обработки и направлена вертикально вверх. Перемещения в направлении оси Y в рассматриваемой модели станка не осуществляются.
Переключение между рабочими системами координат осуществляется программно с помощью соответствующих функций G54–G59 (для систем координат с нулевыми точками W1–W6, соответственно). Координаты нулевых точек W1–6 рассчитываются в системе координат станка относительно машинного нуля M. Синтаксис функций G54–G59 предполагает два возможных варианта их использования. В первом варианте функции задаются без указания координат X и Z. При этом положение выбранной рабочей системы координат определяется по предварительно заданным нулевым корректорам. В данном случае функции G54–G59 могут программироваться отдельно в индивидуальном кадре либо в одном кадре с другими командами. Второй вариант использования функций G54–G59 предполагает программное смещение осей выбранной рабочей системы координат относительно предварительно заданного нуля W1. В данном случае смещения осей по X и Z программируются сразу после функции в этом же кадре (например, «G54×30.5 Z15»). На рисунке 15 показано положение первого начала координат после программного смещения осей в точку [X=10, Z=–20] относительно исходного положения нуля W1, заданного в блоке настройки нулевых корректоров.

Рисунок 15 — Иллюстрация программного смещения осей рабочей системы координат №1
Программирование относительно нуля станка осуществляется посредством функции G53. Данная функция не является модальной, и выполняется в том кадре, в котором она запрограммирована. Функция временно отменяет действие модальных функций G54-G59. При этом все перемещения отсчитываются в системе координат станка с началом в точке M, а активный нулевой корректор временно отменяется. Функция G53 должна программироваться каждый раз, когда необходимо указать координаты, относящиеся к машинному нулю. Синтаксис функции не предполагает наличия параметров после слова G53. Функция программируется в любом кадре, который имеет команды управления пути (например, «G53 G00×0 Z120»). На рисунке 16 показано положение начала рабочей системы координат во время действия функции G53.

Рисунок 16 — Иллюстрация положения начала рабочей системы координат во время действия функции G53
Реализация основных токарных циклов и циклов обработки отверстий
Реализованный алгоритм парсинга управляющих программ позволяет моделировать выполнение токарных и сверлильных циклов системы Fanuc. При выполнении каждого цикла в памяти вычислительного устройства создаётся так называемый буферный список кадров, включающий промежуточные перемещения инструмента при получении запрограммированного контура детали. Токарные циклы задаются одним или двумя последовательными инициирующими кадрами, в которых прописываются основные параметры цикла — черновые и чистовые припуски, глубина резания при черновых проходах резцом, количество черновых проходов резцом, величина отвода резца, параметры режима обработки и т.д. Контур детали программируется последовательностью кадров с обязательной нумерацией первого и последнего кадра.
Цикл снятия припуска параллельно оси Z инициируется функцией G71. Параметры цикла программируются двумя последовательными кадрами в формате:
G71 U_ R_
G71 P_ Q_ U_ W_ F_ S_
где в первом кадре: U — глубина обработки для черновых проходов (режим программирования в радиусах), R — расстояние отвода резца после окончания каждого прохода; во втором кадре: P — порядковый номер первого кадра описания обрабатываемого контура; Q — порядковый номер последнего кадра описания обрабатываемого контура, U — величина и направление снятия чистового припуска по оси X (режим программирования в диаметрах), W — величина и направление снятия чистового припуска по оси Z, F — скорость подачи при черновых проходах резцом, S — частота вращения шпинделя или скорость резания при чистовой обработке.
На рисунке 17 показаны траектории движения резца при выполнении токарного цикла G71. Зелеными линиями изображены перемещения резца на рабочей подаче, фиолетовыми линиями — на ускоренной подаче. Как видно из рисунка, обрабатываемый контур может включать криволинейные участки, запрограммированные методом круговой интерполяции.
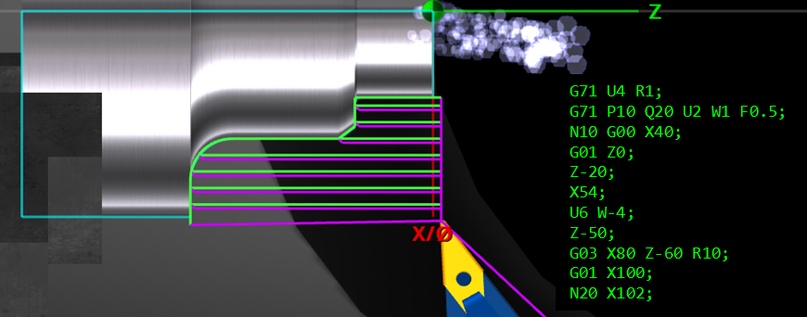
Рисунок 17 — Траектории движения режущего инструмента при выполнении токарного цикла G71 и фрагмент кода управляющей программы
Цикл снятия припуска параллельно оси X инициируется функцией G72. Принцип программирования данного цикла аналогичен циклу G71. Выполнение черновых проходов резцом осуществляется в направлении оси X рабочей системы координат. Параметры цикла программируются двумя последовательными кадрами в формате:
G72 W_ R_
G72 P_ Q_ U_ W_ F_ S_
где в первом кадре: W — глубина обработки для черновых проходов, R — расстояние отвода резца после окончания каждого прохода; во втором кадре: P — порядковый номер первого кадра описания обрабатываемого контура, Q — порядковый номер последнего кадра описания обрабатываемого контура, U — величина и направление снятия чистового припуска по оси X (режим программирования в диаметрах), W — величина и направление снятия чистового припуска по оси Z, F — скорость подачи при черновых проходах резцом, S — частота вращения шпинделя или скорость резания при чистовой обработке.
На рисунке 18 показаны траектории движения резца при выполнении токарного цикла G72.

Рисунок 18 — Траектории движения режущего инструмента при выполнении токарного цикла G72 и фрагмент кода управляющей программы
Цикл снятия припуска параллельно заданному контуру инициируется функцией G73. Параметры цикла программируются двумя последовательными кадрами в формате:
G73 U_ W_ R_
G73 P_ Q_ U_ W_ F_ S_
где в первом кадре: U — величина и направление снятия суммарного припуска по оси X (режим программирования в радиусах), W — величина и направление снятия суммарного припуска по оси Z, R — количество последовательных проходов при снятии чернового припуска, включая получистовой проход; во втором кадре: P — порядковый номер первого кадра описания обрабатываемого контура; Q — порядковый номер последнего кадра описания обрабатываемого контура; U — величина и направление снятия чистового припуска по оси X (режим программирования в диаметрах), W — величина и направление снятия чистового припуска по оси Z, F — скорость подачи при черновых проходах резцом, S — частота вращения шпинделя или скорость резания при чистовой обработке.
На рисунке 19 показаны траектории движения резца при выполнении токарного цикла G73.
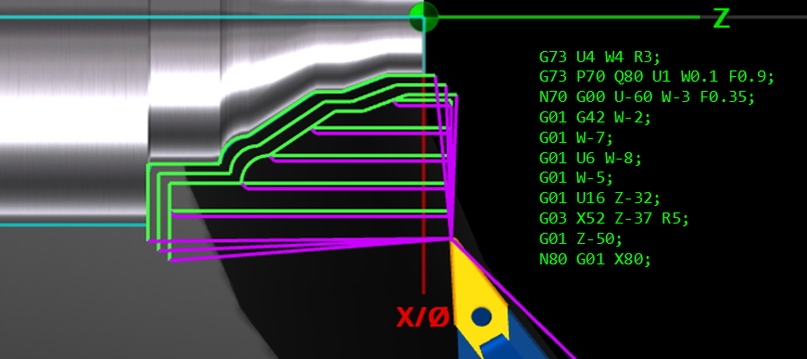
Рисунок 19 — Траектории движения режущего инструмента при выполнении токарного цикла G73 и фрагмент кода управляющей программы
Цикл снятия чистового припуска инициируется функцией G70. Параметры цикла программируются одним кадром в формате:
G70 P_ Q_ F_ S_
где P — порядковый номер первого кадра описания обрабатываемого контура, Q — порядковый номер последнего кадра описания обрабатываемого контура, F — скорость подачи при чистовой обработке, S —
