ИИ и 2048. Часть 2: Минимакс + альфа-бета отсечение
Метод Монте-Карло мы разобрали, сегодня посмотрим, как компьютерный разум играет в 2048, используя старый добрый минимакс с альфа-бета отсечением.
Статья написана при поддержке компании EDISON Software, которая занимается разработкой мобильных приложений и предоставляет услуги по тестированию программного обеспечения.
Решение подсмотрено у пользователя stackoverflow  ovolve, который отметился в обсуждении как ИИ научить в игру 2048.
ovolve, который отметился в обсуждении как ИИ научить в игру 2048.
В настоящее время программа выигрывает примерно в 90% случаев, выполняя java-скрипты в браузере на моем ноутбуке, затрачивая 100 миллисекунд на обдумывание хода, работая хоть и не идеально, но довольно хорошо.
Поскольку игра представляет собой дискретное пространство состояний с полной информацией, по сути являясь пошаговой игрой наподобие шахмат и шашек, я использовал те же методы, которые показали свою работоспособность в этих играх, а именно минимаксный поиск с альфа-бета отсечением. Поскольку по ссылкам приводится много информации об этом алгоритме, я просто расскажу о двух основных эвристиках, которые мной использованы в функции статической оценки и формализующие многие интуитивные предположения, высказываемые здесь другими людьми.

Монотонность
Данная эвристика пытается гарантировать, что все значения плиток либо увеличиваются, либо уменьшаются как влево/вправо, так и вверх/вниз. Одна только эта эвристика отражает ту догадку, о которой упоминали многие другие, что более ценные плитки должны быть сгруппированы в углу. Это, как правило, предотвращает нагромождение менее ценных плиток и держит доску в организованном виде, поскольку меньшие плитки каскадно переходят в бóльшие.
Вот скриншот совершенно монотонной сетки. Я получил это положение, запустив алгоритм с установленной eval-функцией, чтобы игнорировать другие эвристики и учитывать только монотонность.

Плавность (гладкость, ровность)
Вышеприведенная эвристика сама по себе имеет тенденцию создавать структуры, в которых соседние ячейки уменьшаются в стоимости, однако, само собой, для объединения соседи должны иметь одинаковое значение. Поэтому эвристика плавности просто измеряет разницу значений между соседними плитками, стараясь минимизировать их число.
Комментатор на Hacker News дал интересную формализацию этой идеи с точки зрения теории графов.
Вчера я показал эту игру коллеге, любителю теории графов, и мы также решили подумать, как решить эту игру с помощью ИИ.Самым простым решением является минимакс, которое, как я вижу, реализован довольно хорошо. Если кто-то здесь не знаком с минимаксом, OP написал очень элегантный и хорошо прокомментированный код, который был бы отличным пособием.
Менее интенсивный в вычислительном отношении подход, который мы предложили, состоял в том, чтобы смоделировать игровое состояние в виде графа G (V, E), где V — набор активных плиток, а E — набор ребер, соединяющий соседние плитки, взвешенные по функции c (v1, v2), которая возвращает абсолютное значение разницы между двумя плитками. Для каждого решения ИИ выбирает ход, который минимизирует сумму весов всех ребер в новом игровом состоянии.
Причиной этого является то, что единственный способ добиться прогресса в игре — это иметь плитки с одинаковыми значениями рядом друг с другом, для которых вес в G будет равен 0. Таким образом, ИИ должен попытаться минимизировать общий вес. В конце концов на досках будет большое количество с большим весом ребер к соседним плиткам, поэтому ИИ будет стараться держать эти плитки рядом с другими большими плитками, чтобы минимизировать разницу.
Поскольку игра стохастическая, описанный мною подход может не работать в худшем случае, но он также может быть применен к существующему минимаксному решению в качестве весовой функции для каждого узла в дереве.
Вот скриншот совершенно гладкой сетки, любезно предоставленной этим отличным пародийным форком. (ссылка на веб-архив, при этом ява-скрипты на странице работают и Вы с помощью клавиатуры можете сделать ход в любом направлении — примечание переводчика).
Свободные плитки
И, наконец, есть штраф за то, что слишком мало свободных плиток, поскольку варианты могут быстро закончиться, когда игровое поле становится слишком тесным.
И это все! Поиск по игровому пространству при оптимизации этих критериев дает удивительно хорошую производительность. Одним из преимуществ использования обобщенного подхода, подобного этому, а не явно закодированной стратегии перемещения, является то, что алгоритм часто может находить интересные и неожиданные решения. Если вы наблюдаете за его ходом, он часто делает удивительные, но эффективные движения, как, например, внезапную смену стен или углов, вблизи которых он выстраивает свою игру.

Небольшое изменение
Скриншот демонстрирует мощность данного подхода. Я отменил ограничение по значению плиток (чтобы они продолжали расти после достижения значения 2048), и вот лучший результат после восьми испытаний.
Да, это 4096 наряду с 2048. =) Это означает, что он достиг неуловимой плитки 2048 на одной доске.
Код Java-Script для минимакса с альфа-бета отсечением и статической функции оценки от stackoverflow-пользователя ovolve приведён ниже в статье.
Методу минимакса посвящено несколько отличных хабра-статей, поэтому опустим академическое подробное объяснение в чём он заключается. Для тех же, кто присоединился к IT-сообществу совсем недавно слышал красивые термины «минимакс» и «альфа-бета отсечение», но не знает, что сие вообще означает, попробуем, буквально в паре-тройке абзацев пояснить самый общий смысл.
Минимакс
В некоторых играх, процесс игры между двумя игроками (которые делают ход по очереди) можно представить в виде так называемого дерева вариантов. В каждой конкретной позиции каждый игрок, обычно, имеет выбор между разными вариантами своего хода. И в ответ на каждый из этих вариантов соперник может также походить разными способами.

Фрагмент дерева вариантов
Поскольку в любой момент игры о состоянии игрового поля есть полная информация, текущее состояние позиции всегда можно точно оценить. Такая функция носит название статическая функция оценки или сокращённо СФО. При этом, чем большее значение принимает эта функция при оценки конретной позиции, тем более выгодна позиция для одного игрока (назовём его — максимизирующий игрок). Чем меньше при оценке позиции числовое значение этой функции, тем более выгодна позиция для второго игрока (назовём его — минимизирующий игрок).
После каждого хода позиция меняется, а значит и меняется её оценка. При рассмотрении дерева вариантов, каждому игроку необходимо не просто предпочесть те ветки, в которых оценка наиболее благоприятна для него. Также следует избегать тех веток, в которых оценка позиции благоприятна для соперника.
Это и есть минимакс.
Альфа-бета отсечение
Вполне очевидно: кто просчитает от заданной позиции дерево на бóльшую глубину, у того и больше шансов на победу. Но есть одна неприятность — дерево вариантов в играх имеет мерзкую привычку экспоненциально ветвиться и разрастаться с каждым уровнем вложенности. Счётные способности программ и уж тем более людей ограничены, досчитать «вплоть до мата» далеко не всегда возможно. Запросто может оказаться, что игрок досчитал до позиции, где у него хорошая оценка игрового поля, но буквально на следующем (непросчитанном) уровне противник имеет возможность сделать такой ход, который кардинально меняет оценку позиции на противоположную.
Кто виноват и что делать? Виновата вычислительная сложность при полном обходе дерева, бороться предлагается с путём отсечения ненужных веток. Если игрок, оценивающий позицию, видит что какая-то ветка дерева вариантов:
или менее выгодна для него, чем другие ветки, которые уже проанализированы,
или более выгодна для соперника, чем другие ветки, которые уже проанализированы,
то игрок отбрасывает эту ветку, не тратит время и ресурсы на рассмотрение подвариантов из этой заведомо худшей для него ветки.
Это позволяет больше вычислительных ресурсов выделить для расчёта более благоприятных веток на бóльшую глубину просчёта в дереве вариантов. В процесса оценивания игрового поля на разных уровнях дерева вариантов, игрок оперирует двумя динамически меняющимися коэффициентами — альфа (минимально встретившееся в ветке значение СФО — т.е. более благоприятное для минимизирующего игрока) и бета (максимально встретившееся в ветке значение СФО — т.е. более благоприятное для максимизирующего игрока). На каждом уровне сравнение СФО текущей позиции с коэффициентами альфа и бета позволяет отметать (не просчитывая их полностью) ветки, менее выгодные для оценивающего позицию игрока и/или более выгодные для его соперника.
Это и есть альфа-бета отсечение.
Рекурсивная функция минимакса с альфа-бета отсечением
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
''''''''''''''''''''''''''''''''МИНИМАКС'''''''''''''''''''''''''''''''''
'''''''''''''''''''''''(с альфа-бета отсечением)'''''''''''''''''''''''''
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'Оценка позиции с помощью алгоритма минимакса с альфа-бета-отсечением
'Position - матрица 4 на 4 с плитками на ней
'Depth - глубина, на которую считаем
'Alpha, Beta - динамические границы оценок для максимизирующего и минимизирующего игроков
'MaximisingPlayer - это уровень подсчёта для максимизирующго игрока?
Private Function MiniMaxAlpaBeta_Evaluation(Position As Variant, Depth As Long, _
Alpha As Double, Beta As Double, _
MaximisingPlayer As Boolean, _
Optional MainLevel As Boolean = False) As Double
Dim MaxEval As Double 'Правая граница
Dim MinEval As Double 'Левая граница
Dim PositionNext As Variant 'Позиция на следующем ходу игрока
Dim PositionTemp As Variant 'Позиция на следующем ходу игрока
Dim Eval As Double 'Оценка текущего узла
Dim Way As Long 'В каком направлении игрок-человек сдвигает позицию на своём ходе
Dim Row As Long 'Для перебора строк игрового поля
Dim Col As Long 'Для перебора столбцов игрового поля
Dim TileNew As Long 'Размер новой плитки при ходе компьютера
'Если игра завершена (в пользу компьютера, ведь
'игрок неизбежно проиграет рано или поздно)
If GameOverPosition(Position) Then 'Игра в текущей позиции закончена?
'Присваиваем позиции очень низкую оценку
MiniMaxAlpaBeta_Evaluation = -1000000 + TileMax(Position)
'Если углубление вниз по дереву вариантов далее не предполагается
ElseIf Depth = 0 Then
'Оцениваем позицию на достигнутом уровне
MiniMaxAlpaBeta_Evaluation = StaticEvaluation(Position)
'Пока ещё играем, рекурсивно оцениваем позицию
'с точки зрения максимизирующего игрока (человека)
ElseIf MaximisingPlayer Then
MaxEval = -1000000 'Пока что присваиваем позиции минимальную оценку
For Way = 1 To 4 'Все 4 направления хода игрока-человека (вверх, влево, вправо, вниз)
ChangeCount = 0 'Пока неизвестно, будут ли изменения на поле
'Позиция, получаемая после хода в данном направлении
PositionNext = StepHuman(Position, Way)
If ChangeCount > 0 Then 'Есть изменения на игровом поле
'Рекурсивно оцениваем полученную позицию со стороны игрока,
'к которому перейдёт ход (компьютера)
Eval = MiniMaxAlpaBeta_Evaluation(PositionNext, Depth - 1, _
Alpha, Beta, False)
If Eval > MaxEval Then MaxEval = Eval 'Уточняем оценку
'Уточняем границу для максимизирующего игрока
If Eval > Alpha Then Alpha = Eval
'Если ветка заведом менее выгодна, чем те
'что уже рассмотрели - отсекаем всю ветку
If Beta > Alpha Then Exit For
End If
Next
'Итоговое значение выгоды на данном уровне с учётом вложенных уровней
MiniMaxAlpaBeta_Evaluation = MaxEval
'Пока ещё играем, рекурсивно оцениваем позицию
'с точки зрения минимизирующего игрока (компьютера)
Else 'Not MaximisingPlayer
MinEval = 1000000 'Пока что присваиваем позиции максимальную оценку
For Row = 1 To 4 'Перебираем все места игрового поля
For Col = 1 To 4 'Перебираем все места игрового поля
If Position(Row, Col) = 0 Then 'Если место свободно
For TileNew = 2 To 4 Step 2 'Компьютер может поставить или 2 или 4
'Позиция, после того как в этом месте
'компьютер сгенерировал эту плитку
PositionNext = StepComp(Position, Row, Col, TileNew)
'Рекурсивно оцениваем позицию со стороны игрока,
'к которому перейдёт ход (человека)
Eval = MiniMaxAlpaBeta_Evaluation(PositionNext, Depth - 1, _
Alpha, Beta, True)
If Eval < MinEval Then MinEval = Eval 'Уточняем оценку
'Уточняем границу для минимизирующего игрока
If Eval < Beta Then Beta = Eval
'Если ветка заведом менее выгодна, чем те
'что уже рассмотрели - отсекаем всю ветку
If Alpha < Beta Then Exit For
Next
End If
Next
Next
'Итоговое значение выгоды на данном уровне с учётом вложенных уровней
MiniMaxAlpaBeta_Evaluation = MinEval
End If
End Functionfunction AI(grid) {
this.grid = grid;
}
//Статическая функция оценки (СФО)
AI.prototype.eval = function() {
var emptyCells = this.grid.availableCells().length;
var smoothWeight = 0.1,
//monoWeight = 0.0,
//islandWeight = 0.0,
mono2Weight = 1.0,
emptyWeight = 2.7,
maxWeight = 1.0;
return this.grid.smoothness() * smoothWeight
//+ this.grid.monotonicity() * monoWeight
//- this.grid.islands() * islandWeight
+ this.grid.monotonicity2() * mono2Weight
+ Math.log(emptyCells) * emptyWeight
+ this.grid.maxValue() * maxWeight;
};
// alpha-beta depth first search
AI.prototype.search = function(depth, alpha, beta, positions, cutoffs) {
var bestScore;
var bestMove = -1;
var result;
// the maxing player
if (this.grid.playerTurn) {
bestScore = alpha;
for (var direction in [0, 1, 2, 3]) {
var newGrid = this.grid.clone();
if (newGrid.move(direction).moved) {
positions++;
if (newGrid.isWin()) {
return { move: direction, score: 10000, positions: positions, cutoffs: cutoffs };
}
var newAI = new AI(newGrid);
if (depth == 0) {
result = { move: direction, score: newAI.eval() };
} else {
result = newAI.search(depth-1, bestScore, beta, positions, cutoffs);
if (result.score > 9900) { // win
result.score--; // to slightly penalize higher depth from win
}
positions = result.positions;
cutoffs = result.cutoffs;
}
if (result.score > bestScore) {
bestScore = result.score;
bestMove = direction;
}
if (bestScore > beta) {
cutoffs++
return { move: bestMove, score: beta, positions: positions, cutoffs: cutoffs };
}
}
}
}
else { // computer's turn, we'll do heavy pruning to keep the branching factor low
bestScore = beta;
// try a 2 and 4 in each cell and measure how annoying it is
// with metrics from eval
var candidates = [];
var cells = this.grid.availableCells();
var scores = { 2: [], 4: [] };
for (var value in scores) {
for (var i in cells) {
scores[value].push(null);
var cell = cells[i];
var tile = new Tile(cell, parseInt(value, 10));
this.grid.insertTile(tile);
scores[value][i] = -this.grid.smoothness() + this.grid.islands();
this.grid.removeTile(cell);
}
}
// now just pick out the most annoying moves
var maxScore = Math.max(Math.max.apply(null, scores[2]), Math.max.apply(null, scores[4]));
for (var value in scores) { // 2 and 4
for (var i=0; iСтатическая функция оценки
Раз уж на каждом уровне в дереве вариантов приходится оценивать игровое поле (чтобы решить для кого из игроков, собственно, более выгодна оцениваемая позиция), то надо определиться, по каким критериям отличать хорошую позицию от плохой.
Будем считать, что максимизирующий игрок — это человек (или ИИ), который решает, в каком из 4-х направлений (вверх, влево, вправо, вниз) сдвинуть все плитки. А минимизирующий игрок — это та коварная подпрограмма, которая случайно генерирует 2 или 4 в самых неподходящих местах.
СФО составляется с точки зрения максимизирующего игрока. Чем выше даёт оценку СФО для игрового поля — тем лучше позиция для «максималиста». Чем ниже — тем приятнее положение на доске для «минималиста».
В случае с 2048 — какие факторы считать благоприятными для того, кто передвигает плитки?
Монотонность
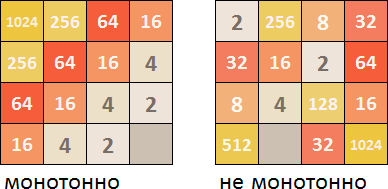
Во-первых, желательно, чтобы плитки были расположены по возрастанию/убыванию в каких-либо направлениях. Если так не делать, то при генерации новых плиток игровое поле быстро станет забитым хаотично расположенными разнокалиберными плитками, которые не получится сразу нормально соединять друг с другом.
В СФО необходимо просмотреть по всем 4-м направлениями (сверху-вниз, слева-направо, справа-налево, снизу-вверх) и посчитать где плитки представляют из себя убывающую или возрастающую прогрессию. Если в прогрессии встречаются плитки, не вписывающиеся в общий ряд, то это уменьшает числовой коэффициент монотонности. Затем из 4-х коэффициентов для всех направлений выбирается наилучший, который и учитывается в итоговом значении СФО.
Плавность

При этом более предпочтительно было бы, если прогрессия из стоящих в ряд плиток была не просто возрастающей, а неубывающей (или вместо убывающего ряда предпочтительнее невозрастающий), то есть хорошо, когда рядом находятся одинаковые плитки, что позволяет схлопывать их в одну, набирая очки и увеличивая свободное пространство на игровом поле.
Поэтому СФО ищет на игровом поле одинаковые рядом стоящие плитки и учитывает количество таких пар в специальном коэффициенте.
Пустые ячейки

Очевидно, что чем больше свободного пространства, тем больше места для манёвра и тем меньше шансов быстро проиграть.
СФО считает пустые ячейки на поле и чем больше таких, тем позиция считается более выгодной для максимизирующего игрока.
Максимальная плитка
Так как главное в этой игре — получить на поле крупную плитку, чем больше тем лучше — 2048, 4096, 8192 (или на что там у вас хватает сил и терпения), то варианты где значение максимальной плитки больше должны СФО считаться как самые выгодные.
СФО для 2048
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'''''''''''''''''''''''СТАТИЧЕСКАЯ ФУНКЦИЯ ОЦЕНКИ''''''''''''''''''''''''
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'Функция статической оценки игрового поля
'Position - матрица 4 на 4 с плитками на ней
Private Function StaticEvaluation(Position As Variant) As Double
Dim Smoothness As Double 'Плавность
Dim Monotonicity As Double 'Монотонность
Dim EmptyCount As Double 'Свободное пространство
Dim MaxValue As Long 'Максимальное значение
'Вес каждой составляющей
Const SmoothWeight = 0.1
Const MonoWeight = 1
Const EmptyWeight = 2.7
Const MaxWeight = 1
Dim k As Long 'Перебор в цикле
Dim i As Long 'Перебор строк
Dim j As Long 'Перебор столбцов
Dim x As Long 'Перебор строк
Dim y As Long 'Перебор столбцов
'Плавность
Dim Value As Double 'Значение текущей ячейки в рамках избранной метрики
'Значение следущей за текущей ячейки в рамках избранной метрики
Dim TargetValue As Double
Smoothness = 0 'Пока плавность не подсчитана
For i = 1 To 4 'Перебираем по строкам игровое поле
For j = 1 To 4 'Перебираем по столбцам игровое поле
If Position(i, j) > 0 Then 'Если непустая ячейка
Value = Log(Position(i, j)) / Log(2)
If i < 4 Then 'Если внизу от ячейки есть ещё место
For x = i + 1 To 4 'Посмотрим вниз от ячейки
If Position(x, j) > 0 Then 'Ближайшее непустое поле снизу
'Значение в избранной метрике
TargetValue = Log(Position(x, j)) / Log(2)
'Разница, характеризующая плавность
Smoothness = Abs(Value - TargetValue)
'После ближайшего пустого поля ячейки не нужны
Exit For
End If
Next
End If
If j < 4 Then 'Если внизу от ячейки есть ещё место
For y = j + 1 To 4 'Посмотрим вправо от ячейки
If Position(i, y) > 0 Then 'Ближайшее непустое поле справа
'Значение в избранной метрике
TargetValue = Log(Position(i, y)) / Log(2)
'Разница, характеризующая плавность
Smoothness = Abs(Value - TargetValue)
'Вслед за ближайшим пустым полем ячейки не нужны
Exit For
End If
Next
End If
End If
Next
Next
'Монотонность
Dim arrTotals(1 To 4) As Double 'Счёт монотонности для каждого направления
Dim Current As Long 'Номер текущей ячейки
Dim Next_ As Long 'Номер следующей непустой ячейки после текущей
Dim CurrentValue As Double 'Значение текущей ячейки в выбранной метрике
Dim NextValue As Double 'Значение следующей за текущей ячейки в выбранной метрике
Monotonicity = 0 'Монотонность пока не вычислили
'Обнулим массив монотонности по всем направлениям
For k = 1 To 4
arrTotals(k) = 0
Next
'Монотонность сверху-вниз и снизу-вверх
For x = 1 To 4 'Перебираем по строкам
Current = 1 'В строке начинаем с первой ячейки
'Следующая за текущей (в данный момент первой в строке) ячейкой
Next_ = Current + 1
Do While Next_ <= 4 'Пока следующая ячейка в пределах игрового поля
'Следующую за текущей ячейку ищем непустую
'(между ней и текущей могут быть пустые клетки)
Do While Next_ <= 4 'Пока следующая ячейка в пределах игрового поля
If Position(x, Next_) = 0 Then 'Если пустая ячейка в ряду
Next_ = Next_ + 1 'Переходим к следующей
Else 'Если НЕ-пустая ячейка в ряду
Exit Do 'Нашли то, что искали, прерываем цикл
End If
Loop
'Если вышли за пределы игрового поля то шаг назад
If Next_ > 4 Then Next_ = 4
'Значения для текущей и следующей непустой ячейки в выбранной метрике
If Position(x, Current) > 0 Then
CurrentValue = Log(Position(x, Current)) / Log(2)
Else
CurrentValue = 0
End If
' MsgBox "Position[" & x & ", " & Next_ & "]=" & Position(x, Next_)
If Position(x, Next_) > 0 Then
NextValue = Log(Position(x, Next_)) / Log(2)
Else
NextValue = 0
End If
If CurrentValue > NextValue Then 'Наблюдается убывание сверху вниз?
arrTotals(Up) = arrTotals(Up) + NextValue - CurrentValue
ElseIf NextValue > CurrentValue Then 'Наблюдается убывание снизу вверх?
arrTotals(Down) = arrTotals(Down) + CurrentValue - NextValue
End If
Current = Next_ 'Следующая непустая за текущей становится сама текущей
Next_ = Next_ + 1 'Следующая за новой текущей
Loop
Next
'К монотонности привосокупляем большее значение из сверху-вниз и снизу-вверх
Monotonicity = IIf(arrTotals(Up) >= arrTotals(Down), _
Monotonicity + arrTotals(Up), _
Monotonicity + arrTotals(Down))
'Монотонность слева-направо и справа-налево
For y = 1 To 4 'Перебираем по столбцам
Current = 1 'В столбце начинаем с первой ячейки
'Следующая за текущей (в данный момент первой в столбце) ячейкой
Next_ = Current + 1
Do While Next_ <= 4 'Пока следующая ячейка в пределах игрового поля
'Следующую за текущей ячейку ищем непустую
'(между ней и текущей могут быть пустые клетки)
Do While Next_ <= 4 'Пока следующая ячейка в пределах игрового поля
If Position(Next_, y) = 0 Then 'Если пустая ячейка в ряду
Next_ = Next_ + 1 'Переходим к следующей
Else 'Если НЕ-пустая ячейка в ряду
Exit Do 'Нашли то, что искали, прерываем цикл
End If
Loop
'Если вышли за пределы игрового поля то шаг назад
If Next_ > 4 Then Next_ = 4
'Значения для текущей и следующей непустой ячейки в выбранной метрике
If Position(Current, y) > 0 Then
CurrentValue = Log(Position(Current, y)) / Log(2)
Else
CurrentValue = 0
End If
If Position(Next_, y) > 0 Then
NextValue = Log(Position(Next_, y)) / Log(2)
Else
NextValue = 0
End If
If CurrentValue > NextValue Then 'Наблюдается убывание сверху вниз?
arrTotals(Left) = arrTotals(Left) + NextValue - CurrentValue
ElseIf NextValue > CurrentValue Then 'Наблюдается убывание снизу вверх?
arrTotals(Right) = arrTotals(Right) + CurrentValue - NextValue
End If
Current = Next_ 'Следующая непустая за текущей становится сама текущей
Next_ = Next_ + 1 'Следующая за новой текущей
Loop
Next
'К монотонности привосокупляем большее значение из справа-налево и слева-направо
Monotonicity = IIf(arrTotals(Left) >= arrTotals(Right), _
Monotonicity + arrTotals(Left), _
Monotonicity + arrTotals(Right))
'Свободное пространство и максимальная плитка
EmptyCount = 0 'Пока не подсчитали количество свободных ячеек
MaxValue = 0 'Пока неизвестно максимальное значение
For i = 1 To 4 'Перебираем по строкам игровое поле
For j = 1 To 4 'Перебираем по столбцам игровое поле
If Position(i, j) = 0 Then 'Если пустая ячейка...
'... то подсчитываем свободное пространство
EmptyCount = EmptyCount + 1
'Если непустая и больше текущего максимума...
ElseIf Position(i, j) > MaxValue Then
MaxValue = Position(i, j) '... то уточняем максимум
End If
Next
Next
'Итоговое значение функции
StaticEvaluation = Smoothness * SmoothWeight + _
Monotonicity * MonoWeight + _
Log_Base_Arg(EmptyCount) * EmptyWeight + _
MaxValue * MaxWeight
End Functionfunction Grid(size) {
this.size = size;
this.startTiles = 2;
this.cells = [];
this.build();
this.playerTurn = true;
}
// pre-allocate these objects (for speed)
Grid.prototype.indexes = [];
for (var x=0; x<4; x++) {
Grid.prototype.indexes.push([]);
for (var y=0; y<4; y++) {
Grid.prototype.indexes[x].push( {x:x, y:y} );
}
}
// Build a grid of the specified size
Grid.prototype.build = function () {
for (var x = 0; x < this.size; x++) {
var row = this.cells[x] = [];
for (var y = 0; y < this.size; y++) {
row.push(null);
}
}
};
// Find the first available random position
Grid.prototype.randomAvailableCell = function () {
var cells = this.availableCells();
if (cells.length) {
return cells[Math.floor(Math.random() * cells.length)];
}
};
Grid.prototype.availableCells = function () {
var cells = [];
var self = this;
this.eachCell(function (x, y, tile) {
if (!tile) {
//cells.push(self.indexes[x][y]);
cells.push( {x:x, y:y} );
}
});
return cells;
};
// Call callback for every cell
Grid.prototype.eachCell = function (callback) {
for (var x = 0; x < this.size; x++) {
for (var y = 0; y < this.size; y++) {
callback(x, y, this.cells[x][y]);
}
}
};
// Check if there are any cells available
Grid.prototype.cellsAvailable = function () {
return !!this.availableCells().length;
};
// Check if the specified cell is taken
Grid.prototype.cellAvailable = function (cell) {
return !this.cellOccupied(cell);
};
Grid.prototype.cellOccupied = function (cell) {
return !!this.cellContent(cell);
};
Grid.prototype.cellContent = function (cell) {
if (this.withinBounds(cell)) {
return this.cells[cell.x][cell.y];
} else {
return null;
}
};
// Inserts a tile at its position
Grid.prototype.insertTile = function (tile) {
this.cells[tile.x][tile.y] = tile;
};
Grid.prototype.removeTile = function (tile) {
this.cells[tile.x][tile.y] = null;
};
Grid.prototype.withinBounds = function (position) {
return position.x >= 0 && position.x < this.size &&
position.y >= 0 && position.y < this.size;
};
Grid.prototype.clone = function() {
newGrid = new Grid(this.size);
newGrid.playerTurn = this.playerTurn;
for (var x = 0; x < this.size; x++) {
for (var y = 0; y < this.size; y++) {
if (this.cells[x][y]) {
newGrid.insertTile(this.cells[x][y].clone());
}
}
}
return newGrid;
};
// Set up the initial tiles to start the game with
Grid.prototype.addStartTiles = function () {
for (var i=0; i= 0 && x <= 3 && y >= 0 && y <= 3 &&
self.cells[x][y] &&
self.cells[x][y].value == value &&
!self.cells[x][y].marked ) {
self.cells[x][y].marked = true;
for (direction in [0,1,2,3]) {
var vector = self.getVector(direction);
mark(x + vector.x, y + vector.y, value);
}
}
}
var islands = 0;
for (var x=0; x<4; x++) {
for (var y=0; y<4; y++) {
if (this.cells[x][y]) {
this.cells[x][y].marked = false
}
}
}
for (var x=0; x<4; x++) {
for (var y=0; y<4; y++) {
if (this.cells[x][y] &&
!this.cells[x][y].marked) {
islands++;
mark(x, y , this.cells[x][y].value);
}
}
}
return islands;
}
// measures how smooth the grid is (as if the values of the pieces
// were interpreted as elevations). Sums of the pairwise difference
// between neighboring tiles (in log space, so it represents the
// number of merges that need to happen before they can merge).
// Note that the pieces can be distant
Grid.prototype.smoothness = function() {
var smoothness = 0;
for (var x=0; x<4; x++) {
for (var y=0; y<4; y++) {
if ( this.cellOccupied( this.indexes[x][y] )) {
var value = Math.log(this.cellContent( this.indexes[x][y] ).value) / Math.log(2);
for (var direction=1; direction<=2; direction++) {
var vector = this.getVector(direction);
var targetCell = this.findFarthestPosition(this.indexes[x][y], vector).next;
if (this.cellOccupied(targetCell)) {
var target = this.cellContent(targetCell);
var targetValue = Math.log(target.value) / Math.log(2);
smoothness -= Math.abs(value - targetValue);
}
}
}
}
}
return smoothness;
}
Grid.prototype.monotonicity = function() {
var self = this;
var marked = [];
var queued = [];
var highestValue = 0;
var highestCell = {x:0, y:0};
for (var x=0; x<4; x++) {
marked.push([]);
queued.push([]);
for (var y=0; y<4; y++) {
marked[x].push(false);
queued[x].push(false);
if (this.cells[x][y] &&
this.cells[x][y].value > highestValue) {
highestValue = this.cells[x][y].value;
highestCell.x = x;
highestCell.y = y;
}
}
}
increases = 0;
cellQueue = [highestCell];
queued[highestCell.x][highestCell.y] = true;
markList = [highestCell];
markAfter = 1; // only mark after all queued moves are done, as if searching in parallel
var markAndScore = function(cell) {
markList.push(cell);
var value;
if (self.cellOccupied(cell)) {
value = Math.log(self.cellContent(cell).value) / Math.log(2);
} else {
value = 0;
}
for (direction in [0,1,2,3]) {
var vector = self.getVector(direction);
var target = { x: cell.x + vector.x, y: cell.y+vector.y }
if (self.withinBounds(target) && !marked[target.x][target.y]) {
if ( self.cellOccupied(target) ) {
targetValue = Math.log(self.cellContent(target).value ) / Math.log(2);
if ( targetValue > value ) {
//console.log(cell, value, target, targetValue);
increases += targetValue - value;
}
}
if (!queued[target.x][target.y]) {
cellQueue.push(target);
queued[target.x][target.y] = true;
}
}
}
if (markAfter == 0) {
while (markList.length > 0) {
var cel = markList.pop();
marked[cel.x][cel.y] = true;
}
markAfter = cellQueue.length;
}
}
while (cellQueue.length > 0) {
markAfter--;
markAndScore(cellQueue.shift())
}
return -increases;
}
// measures how monotonic the grid is. This means the values of the tiles are strictly increasing
// or decreasing in both the left/right and up/down directions
Grid.prototype.monotonicity2 = function() {
// scores for all four directions
var totals = [0, 0, 0, 0];
// up/down direction
for (var x=0; x<4; x++) {
var current = 0;
var next = current+1;
while ( next<4 ) {
while ( next<4 && !this.cellOccupied( this.indexes[x][next] )) {
next++;
}
if (next>=4) { next--; }
var currentValue = this.cellOccupied({x:x, y:current}) ?
Math.log(this.cellContent( this.indexes[x][current] ).value) / Math.log(2) :
0;
var nextValue = this.cellOccupied({x:x, y:next}) ?
Math.log(this.cellContent( this.indexes[x][next] ).value) / Math.log(2) :
0;
if (currentValue > nextValue) {
totals[0] += nextValue - currentValue;
} else if (nextValue > currentValue) {
totals[1] += currentValue - nextValue;
}
current = next;
next++;
}
}
// left/right direction
for (var y=0; y<4; y++) {
var current = 0;
var next = current+1;
while ( next<4 ) {
while ( next<4 && !this.cellOccupied( this.indexes[next][y] )) {
next++;
}
if (next>=4) { next--; }
var currentValue = this.cellOccupied({x:current, y:y}) ?
Math.log(this.cellContent( this.indexes[current][y] ).value) / Math.log(2) :
0;
var nextValue = this.cellOccupied({x:next, y:y}) ?
Math.log(this.cellContent( this.indexes[next][y] ).value) / Math.log(2) :
0;
if (currentValue > nextValue) {
totals[2] += nextValue - currentValue;
} else if (nextValue > currentValue) {
totals[3] += currentValue - nextValue;
}
current = next;
next++;
}
}
return Math.max(totals[0], totals[1]) + Math.max(totals[2], totals[3]);
}
Grid.prototype.maxValue = function() {
var max = 0;
for (var x=0; x<4; x++) {
for (var y=0; y<4; y++) {
if (this.cellOccupied(this.indexes[x][y])) {
var value = this.cellContent(this.indexes[x][y]).value;
if (value > max) {
max = value;
}
}
}
}
return Math.log(max) / Math.log(2);
}
// WIP. trying to favor top-heavy distributions (force consolidation of higher value tiles)
/*
Grid.prototype.valueSum = function() {
var valueCount = [];
for (var i=0; i<11; i++) {
valueCount.push(0);
}
for (var x=0; x<4; x++) {
for (var y=0; y<4; y++) {
if (this.cellOccupied(this.indexes[x][y])) {
valueCount[Math.log(this.cellContent(this.indexes[x][y]).value) / Math.log(2)]++;
}
}
}
var sum = 0;
for (var i=1; i<11; i++) {
sum += valueCount[i] * Math.pow(2, i) + i;
}
return sum;
}
*/
// check for win
Grid.prototype.isWin = function() {
var self = this;
for (var x=0; x<4; x++) {
for (var y=0; y<4; y++) {
if (self.cellOccupied(this.indexes[x][y])) {
if (self.cellContent(this.indexes[x][y]).value == 2048) {
return true;
}
}
}
}
return false;
}
//Grid.prototype.zobristTable = {}
//for
//Grid.prototype.hash = function() {
//} 2048.xlsm
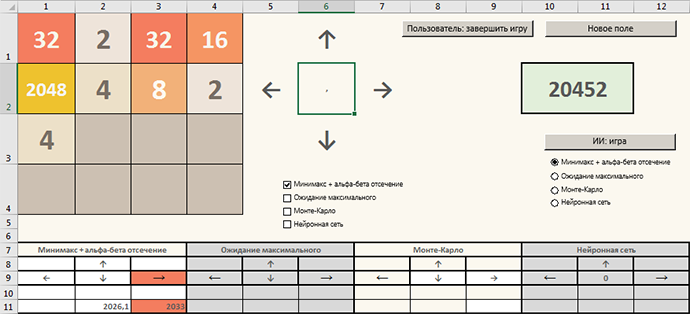
Само Excel-приложение можно скачать с гугл-диска.
Функционал приложения описан в предыдущей статье, где ИИ играет с помощью метода Монте-Карло. К уже имеющемуся Монте-Карло добавлено сегодняшнее решение.

