Играть на уровне бога: как ИИ научился побеждать человека

В 16 играх машины одолели человека (в 17, если брать в расчет поражение Ли Седоля в го), но в будущем их ждут еще более впечатляющие достижения: решение самых ошеломляющих математических, физиологических и биологических проблем, победа над болезнями и старостью, ликвидация дорожных аварий, триумф в военных конфликтах и многое другое.
Мир изменился прямо на наших глазах, но не все заметили это. Когда и как программы научились играть безошибочно? Всегда ли проигрыш одного человека свидетельствует о поражении всего человечества? Обретет ли искусственный интеллект сознание?
Об авторе. Статья основана на лекции «Искусственный интеллект. История и перспективы», проведенной в московском офисе Mail.Ru Group Сергеем Марковым. Сергей Марков занимается machine learning в «Сбербанке». В банковской сфере строят предиктивные модели для управления бизнес-процессом на основе достаточно больших обучающих выборок, которые могут включать несколько сотен миллионов кейсов. Среди своих хобби Сергей указывает шахматное программирование, ИИ для игр, минимаксные задачи. Программа SmarThink, созданная Сергеем Марковым, становилась чемпионом России (2004) и СНГ (2005) среди шахматных программ (2004), и сегодня входит в топ-30 сильнейших программ в мире. Также Сергей является основателем некоммерческого научно-просветительского портала 22 век.

TechnoCore — место обитания множества искусственных интеллектов в тетралогии «Песен Гипериона» Дэна Симмонса. Один из примеров визуализации сильных ИИ в научной фантастике.
С самим понятием ИИ произошла неприятная история. Появившись изначально в научной сфере среди специалистов, работавших в области computer science, оно очень быстро попало в публичную среду и претерпело различные изменения. Если сегодня спросить обывателя о том, что такое ИИ, скорее всего, вы услышите от него совсем не то определение, которое держат в голове специалисты по ИИ.
Прежде чем начать рассказ, нужно определиться, что именно мы понимаем под искусственным интеллектом, и где находится граница, на которой заканчивается область compute rscience и начинаются смежные области.
ИИ вообще — это методы, используемые для автоматизации задач, которые традиционно считаются задачами интеллектуальными, и для решения которых человек задействует свой естественный интеллект. Автоматизируя задачу, решаемую человеком с помощью мозга, мы тем самым создаем ИИ. Другое дело, что такой ИИ обычно называют прикладным или, с некоторой долей презрения, слабым. Неприятный нюанс в том, что это единственный доступный человечеству на сегодняшний день вид ИИ.
Что касается сильного ИИ, artificial general intelligence (AGI), определенные наработки здесь есть, но пока мы в самом начале пути. Сильный ИИ — это система, способная решать любые интеллектуальные задачи. В фантастике сформировался образ именно такого, подобного человеку, ИИ, способного решать любую задачу.

Поскольку мы так широко в computer science определяем искусственный интеллект, то с формальной точки зрения найдем элементы существования ИИ еще у древних греков. Речь идет о знаменитом Антикитерском механизме, являющемся одним из неуместных артефактов. Это устройство предназначено для астрофизических расчетов. На фотографии выше представлен один из сохранившихся фрагментов и современная реконструкция артефакта. Механизм содержал 37 бронзовых шестерен в деревянном корпусе, на котором были размещены циферблаты со стрелками. Восстановить положение шестерен внутри покрытых минералом фрагментов удалось методом компьютерной томографии с помощью рентгеновских лучей.
Сама по себе задача счета когда-то считалась интеллектуальной — если человек умел хорошо считать, то его можно было назвать интеллектуалом.

Счетный прибор Джона Непера, предназначенный для быстрого умножения.
Задачи счета автоматизировались одними из первых. Еще до первых механических устройств появились поделки типа неперовых палочек. Шотландский математик, один из изобретателей логарифмов Джон Непер, создал устройство счета в 1617 г. На фоне современных технологий оно кажется смешным: рулоны бумаги — по сути, первые логарифмические таблицы для выполнения некоторых операций. Но для современников это было примерно таким же чудом, как для нас какой-нибудь AlphaGo. В свое время были даже поэты, посвящавшие неперовым палочкам (Napier«s bones) стихи. Дескать, почему вы носитесь с костями предков, вот те самые кости, которыми действительно стоит гордиться.

Суммирующая машина Паскаля — арифметическая машина, изобретенная французским ученым Блезом Паскалем в 1642 г.
Паскаль, наравне с немецким математиком Вильгельмом Шикардом, предложившим свою версию вычислительной машины в 1623 г., заложил основы для появления большинства вычислительных устройств. До наших дней сохранились несколько машин, созданных еще при жизни Паскаля. Такая машина умела складывать, делить, вычитать и умножать.

Полная рабочая копия машины, изобретенной английским математиком Чарльзом Бэббиджем в 1822 г. Так называемая разностная машина предназначена для автоматизации вычислений путем аппроксимации функций многочленами и вычисления конечных разностей.
О Чарльзе Бэббидже слышали практически все компьютерные специалисты. Увы, Бэббидж так и не смог создать работающую вычислительную машину. Долгое время не утихали споры, работает ли в принципе предложенная им разностная машина. В период с 1989 по 1991 г., к 200-летию со дня рождения Чарльза Бэббиджа, по сохранившимся чертежам и с небольшими модификациями была собрана работающая копия аналитической машины. Модификации понадобились из-за «багов», обнаруженных в чертежах. Возможно, Бэббидж намеренно сделал несколько искажений, борясь с нелицензионным пиратским копированием.
Аналитическая машина — это прообраз современных фон-неймановских машин. Когда инженеры IBM строили первую электронную машину, они использовали чертежи Бэббиджа. Мы привыкли говорить о фон-неймановской архитектуре, то есть машине с разнесенным вычислительным устройством, с устройством ввода-вывода, с памятью и т.д. Однако в основе находятся идеи Бэббиджа.
К тому же в машинном коде бэббиджевой машины применялись оператор условного ветвления и оператор цикла. Эту машину действительно можно считать прадедом того, что потом удалось сделать на основе электроники.

Жаккардова машина — зевообразовательный механизм ткацкого станка для выработки крупноузорчатых тканей. Создан в 1804 г. Позволяет раздельно управлять каждой нитью основы или небольшой их группой.
Устройства ввода-вывода, перфокарты появились еще до Бэббиджа — они использовались в ткацких жаккардовских станках, чтобы задавать порядок следования нитей при изготовлении ткани.

Табулятор — электромеханическая машина, предназначенная для автоматической обработки числовой и буквенной информации, записанной на перфокартах.
Первый статистический табулятор построен американцем Германом Холлеритом в 1890 г. для решения задач, связанных со статистическими расчетами. Известный изобретатель и создатель оборудования для работы с перфокартами успешно принял участие в конкурсе, организованном правительством США для поиска средств автоматизации обработки результатов переписи населения. Для ручного подсчета и анализа понадобилось бы порядка 100 человек, работающих в течение 4–5 лет, чтобы просто обобщить и посчитать суммарные социологические показатели переписи.
Перфокарта Холлерита.
Табулятор — это очень примитивная сводная таблица. Каждая карточка соответствует анкете, в ней проделаны отверстия, соответствующие ответу. Карточки загружались в табулятор, он быстро прогонял их через себя и выдавал результат в виде такой же карты с подсчитанной суммой. Эти суммы вкладывались в другой табулятор и т.д.
Выиграв конкурс, Холлерит основал свою компанию — Tabulating machines company, и после некоторой череды слияний и поглощений она стала называться IBM.
Как и во всякой экспериментальной науке, разделу computer sciencе, занимающемуся ИИ, нужна была своя мушка дрозофила, некий модельный объект, на котором можно было опробовать методы ИИ. Игра — самая известная мушка дрозофила в сфере ИИ.
Игра — чистое модельное пространство. В ней заданы условия, состояния, однозначно определенные и описываемые в виде набора параметров. Создавая ИИ для игры, мы тем самым абстрагируемся от массы инженерных проблем, лежащих между ИИ и практическим решением задачи. Мы абстрагируемся от кодирования данных на входе и выходе, от преобразования сигнала, задачи восприятия и т.д. Для нас интеллектуальная задача существует в игре в чистом виде. Это удобно, потому что специалисты по ИИ ленивые и не хотят заниматься ничем, кроме ИИ.

Шахматная машина «Турок».
Игра — это зрелище. Если вы покажете машину, умеющую хорошо играть, она произведет впечатление даже на несведущего человека. Игра машины привлекает внимание уже сотни лет. На картинке выше вы видите иллюстрацию знаменитой мистификации — первый шахматный автомат, сконструированный изобретателем Вольфгангом фон Кемпеленом в 1769 г. Внутри «машины» на самом деле прятался настоящий шахматист. В эту коробку не брезговали залезть ведущие шахматисты своего времени. Иоганн Баптист Альгайер, сильнейший шахматист Австрии конца XVIII — начала XIX вв., сыграл за шахматный автомат целый ряд партий.
Это сложное механическое устройство не является искусственным интеллектом, но любопытно то, что с его помощью удалось одурачить современников. Люди действительно верили, что какой-то искусный мастер смог при помощи шестеренок, рычажков, механизмов и противовесов создать систему, способную играть в шахматы. Сохранилась даже запись партии, сыгранной механическим турком против Наполеона (впрочем, некоторые историки подвергают его достоверность сомнению). Так что, возможно, что одурачены были даже высшие особы.

А это уже первое устройство, которое на самом деле умело играть в шахматы. El Ajedrecista (в переводе на русский — «шахматный игрок»). Его создал в 1912 г. известный испанский математик и инженер Леонардо Торрес Кеведо.
El Ajedrecista представлял собой шахматную доску, на которой машина с помощью электромагнитов передвигала короля и ладью. Машина гарантированно ставила мат королем и ладьей одинокому королю из одной позиции: король стоял у белых на Н8, ладья — на G7, а черный король мог стоять на любом поле. Два сохранившихся экземпляра машины выставлены в Политехническом музее Мадрида.

Это другой знаменитый ИИ прошлого — механизм «Ниматрон», созданный в 1940 г. для игры в Ним. Ним — математическая игра, в которой два игрока по очереди берут предметы, разложенные на несколько кучек (обычно три). За один ход можно взять любое количество предметов (больше нуля) из одной кучки. Выигрывает игрок, взявший последний предмет.
Это одна из первых игр, для которых построили полную математическую теорию еще в 1901—1902 гг. С точки зрения методов «Ниматрон» ничего нового не представлял, опираясь на уже известную оптимальную стратегию для этой игры, но был одним из первых решений теории игр в железе.
Проектом «Ниматрон» руководил Эдвард Улер Кондон — один из отцов современной квантовой механики. Он считал этот проект самой большой неудачей в своей жизни, но не с технической, а с финансовой стороны. Работая над «Ниматроном», Кондон со своей командой изобрел множество технологий (среди которых, например, способ изготовления печатных плат), которые потом были востребованы в компьютерной технике. Но команда специалистов ничего не запатентовала, в результате ничего и не заработала.

Эрнст Фридрих Фердинанд Цермело — немецкий математик, внесший значительный вклад в теорию множеств и создание аксиоматических оснований математики.
Разговор об искусственном интеллекте для игр не обходится без упоминания Эрнста Цермело и его теоремы. Русскоязычным любителям этой темы повезло. Работа Цермело изначально была написана на немецком языке. И если на английский ее перевели только в 1999 г., то на русский язык — еще в конце 1960-х — начале 1970-х годов. Из-за этого в русскоязычной литературе написано более-менее правильно про то, что Цермело сделал, а в англоязычной литературе путаются до сих пор. Например, в одной из работ говорится о том, что Цермело доказал, что если белые в шахматах будут совершать идеальные ходы, то обязательно достигнут как минимум ничьи. На самом деле никто на сегодняшний день таких доказательств не предоставил, однако Цермело сделал другое важное открытие.
Он не очень хорошо играл в шахматы, да и вообще плохо знал правила игры. Может, благодаря этому и доказал в 1913 г. первую формальную теорему теории игр. Согласно книге «Управляемые процессы и теория игр», изданной в СССР в 1955 г., корректное описание вклада Цермело звучит так: «Цермело доказал детерминизм игр, подобных шахматам, и то, что рациональные игроки могут, используя полную информацию, разработать оптимальную стратегию игры».
Обычные правила игры в шахматы знают почти все, однако есть несколько других очень важных и не совсем очевидных правил. Например, правило 50 ходов гласит, что если в течение 50 ходов ни одна пешка не двинулась вперед и ни одна фигура не была взята, то присуждается ничья. Или если какая-то позиция повторилась трижды — также присуждается ничья. Бесконечной партии в шахматах по количеству ходов быть не может — в какой-то момент игра так или иначе прекратится. Эрнст Цермело не знал этого, и думал, что в шахматах возможны бесконечные партии: вы пошли фигурой — вернули, и так играете, пока вселенная не рассыплется в пыль.
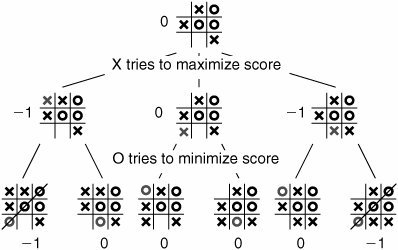
Итак, давайте посмотрим, как рассчитывается оптимальная стратегия игры. Немного отвлечемся от шахмат, возьмем более простой пример — крестики-нолики, одну из древнейших игр в мире, появившуюся еще в Древнем Египте. Для этой игры Цермело использовал обратную индукцию — метод, с помощью которого проводят поиск в обратном направлении: начиная с позиций, где одна из сторон уже получила пат или мат, и заканчивая конкретной позицией, стоящей на доске.
Цермело не давал подробного описания обратной индукции, но использовал ее принцип, согласно которому существует позиция, выигрышная для одной из сторон. Мы для таких позиций можем назначить оценку: –1 — выиграли нолики, 1 — выиграли крестики, 0 — ничья.
Теперь можем пойти вверх по дереву от этих позиций и посмотреть, есть ли ход с какой-то позиции, ведущий в выигрышную позицию. Если ход существует, то и позиция считается выигрышной.
С другой стороны, если нет ни одного хода, ведущего в выигрышную позицию, но есть хотя бы один ход, ведущий в ничейную позицию, то эта позиция считается ничейной. И если нет ни одного хода, ведущего ни в ничейную, ни в выигрышную позицию, то позиция считается проигранной.
Пользуясь этим правилом, мы в дереве, начиная с листьев, двигаемся вверх, и приписываем оценки узлам, пока не припишем оценки всем позициям. Получив все оценки для всех позиций, видим идеальный алгоритм для игры. Оказавшись в какой-то позиции игры, мы всегда будем видеть ход (если он есть), ведущий в выигрышную позицию. Если выигрышного хода нет, то будем делать ничейный ход, и только в худшем случае пойдем в проигрышную позицию. Теоретически такая система, способная хранить в памяти дерево оценки для каждой позиции, будет играть на уровне бога.
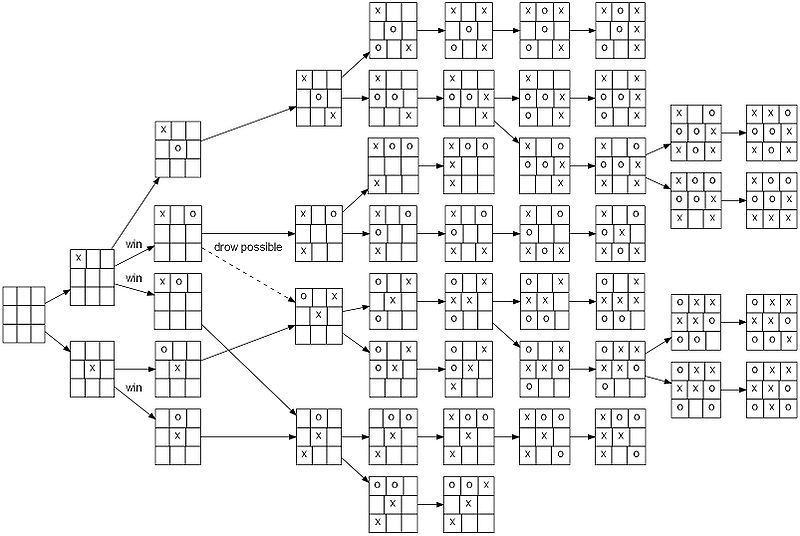
Цермело это понимал, но считал, что у этого дерева есть бесконечные ветви, где нет терминальных позиций. Он задался вопросом: можно ли для игры, имеющей бесконечное дерево по размеру позиций в нем, за конечное время посчитать оптимальную стратегию, то есть гарантированно в каждой позиции делать идеальный ход? И доказал, что несмотря на то, что само дерево может быть бесконечным, мы можем найти оптимальную стратегию за конечное число итераций. И это конечное число итераций точно не превышает количество разных позиций в игре.

EDSAC (Electronic Delay Storage Automatic Calculator) — первый в мире действующий и практически используемый компьютер с хранимой в памяти программой, созданный в 1949 г. в Кембриджском университете (Великобритания). В 1952 г. реализация игры в крестики-нолики для компьютера EDSAC стала одной из первых видеоигр. Компьютер научился играть идеальные игры против человека, оперируя известной ему оптимальной стратегией.

Экономист Оскар Моргенштерн, один из авторов теории игр, и математик Джон фон Нейман, сделавший важный вклад в квантовую физику, функциональный анализ, теорию множеств и другие отрасли науки.
Работа про интерпретацию обратной индукции находится в области теории множеств. Другая сфера знаний, без которой невозможно представить развитие теории игр, лежит в области экономики. В 1944 г. вышла монография Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение», в которой авторы обобщили и развили результаты теории игр и предложили новый метод для оценки полезности благ. В этой работе впервые формально было дано определение метода обратной индукции.

В 1965 г. математик Ричард Белман предложил использовать метод ретроспективного анализа для создания баз данных решений шахматных и шашечных эндшпилей (заключительная часть партии). Он дал алгоритмическое описание применения метода обратной индукции для построения оптимальной стратегии в играх.

В 1970 г. математик Томас Штрохлейн защитил докторскую диссертацию о шахматном окончании. Дело в том, что в шахматах существуют специальные случаи, когда на доске остается мало фигур. В таких случаях для небольшого числа фигур мы можем решить задачу методом обратной индукции.
Итак, мы приблизились к пониманию, каким образом ИИ выигрывает у человека в шахматы. Компьютеру не нужно каждый раз производить расчеты эндшпиля — достаточно посмотреть в базе данных уже посчитанный результат и сделать идеальный ход. Эндшпильные базы данных, включающие все возможные расстановки фигур, проводят поиск в обратном направлении, начиная с позиций, где одна сторона уже получила пат или мат, и заканчивая конкретной позицией на доске.

В 1977 г. Кен Томпсон, известный за вклад в создание языка С и ОС UNIX, представил одну из первых в мире эндшпильных таблиц для всех пятифигурных окончаний.
В 1998 г. наш соотечественник, программист Евгений Налимов создал чрезвычайно эффективный генератор шахматных окончаний, благодаря которому, учитывая рост производительности компьютеров, к началу 2000-х годов были посчитаны все шестифигурные окончания.

Эту главу закроет фотография не человека, а компьютера. В 2012 г. рассчитали семифигурные таблицы для ситуаций распределения фигур четыре против трех и пять против двух. Их назвали таблицами «Ломоносова», так как рассчитывались они на суперкомпьютерах МГУ «Ломоносов» и IBM BlueGene/P.
Участие компьютеров в шахматных играх открыло людям то, о чем никто не догадывался сотни лет. Как уже упоминалось, в шахматах существует правило 50 ходов. Было известно, что есть очень редкие исключения, когда игрокам требовалось более 50 ходов для хитрых маневров. Однако когда Кен Томпсон начал публиковать результаты анализа, оказалось, что этих исключений очень много.
Эксперты ФИДЕ (Federation Internationale des Echecs — Международная шахматная федерация) предложили заменить правило 50 ходов на правило 75 ходов, что и было сделано.

Вскоре выяснилось, что в ряде случаев для завершения партии недостаточно и 75 ходов, но и на этом процесс поиска новых решений не остановился. На сегодняшний день рекордная задача — мат в 549 ходов.
В итоге ФИДЕ на это дело плюнули и решили вернуться к правилу 50 ходов. В конце концов, неужели мы будем подыгрывать компьютерам? Ни один человек со стандартным размером мозга не способен найти последовательность из сотен тихих ходов, ведущих к победе.
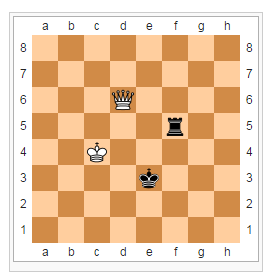
Кен Томпсон провел несколько показательных выступлений — «ладья и король против ферзя и короля». Компьютер играл за игрока, владеющего ладьей. Этот эндшпиль теоретически проигрышный — шахматист уровня мастера, владея ферзем, обычно легко выигрывает у любого противника. Компьютеру была поставлена задача максимально оттянуть свой теоретически неизбежный проигрыш. На одном из выступлений против компьютера играли Ханс Берлинер, чемпион мира в игре по переписке, со своим другом — сильным гроссмейстером из топ-30 мировых игроков. И двум гроссмейстерам не удалось заматовать короля. На доске происходило нечто феерическое — происходили неясные маневры, но черным чудесным образом удавалось выпутаться. Это была одна из первых прекрасных демонстраций того, что люди, возможно, переоценивают себя в понимании некоторых вещей.
Фрагмент листинга шахматной программы ИТЭФ для ЭВМ М-20.
Первый матч между двумя шахматными программами состоялся в 1967 г. Играли программа Института теоретической и экспериментальной физики и программа Стэнфордского университета. Сохранился исходный код программы ИТЭФ, скачать его можно здесь.
На основе исходных текстов программы ИТЭФ началось создание новой шахматной программы, получившей название «Каисса». В 1974 г. Каисса стала первым чемпионом мира по шахматам среди компьютерных программ. Многие алгоритмы, придуманные авторами Каиссы, до сих пор применяются в шахматах. Каисса применила алгоритм отсечения позиций, и впервые — побитовое представление доски. Также она могла производить анализ во время хода соперника, использовала эвристику нулевого хода и сложные алгоритмы для управления временем.
Если заучить эти таблицы, вы сможете идеально играть в крестики-нолики с любым противником.
Все решения задач с ограниченными модельными пространствами делятся на три вида. Первый вид — ультраслабое решение, когда для какой-то игры мы можем точно сказать, каким будет результат, но при этом не будет алгоритма, позволяющего в любой ситуации играть идеально. Обычно это какой-то трюк, например, повторение стратегии. Мы знаем, что для некоторых игр второй игрок может копировать ходы первого игрока, и тогда он достигнет ничьей.
Второй вид — слабое решение. В этом случае мы начинаем со стартовой позиции, делаем любые ходы, а машина совершает ходы, которые считает идеальными. Она всегда будет ходить идеально, но если мы какой-то ход сделаем за машину, то попадем в позицию, где нет определенной оценки, и непонятно, как играть дальше. Идеальный ход есть только в том случае, если с самого начала игры совершались идеальные ходы.
И третий вид — сильное решение. Для каждой позиции мы знаем ее точную оценку. Например, для крестиков-ноликов точно знаем дерево ходов — около 900 позиций, если учесть все симметрии.
29 апреля 2007 г. команда исследователей из Университета Альберты (Канада) под руководством Д. Шеффера (известного как ведущий разработчик шашечной программы «Чинук») смогла достичь «слабого» решения для английских шашек, по правилам которых шашки не бьют назад, а дамки не могут ходить на любое расстояние.
Английские шашки — самая большая из игр, решенных до настоящего времени. Размер ее поискового пространства 5×1020. Для того чтобы найти решение, в течение 18 лет сеть персональных компьютеров (в разное время от 50 до 200) произвела 1014 вычислений.

На начало 2016 г. найдено решение в 16 играх. Последней на данный момент решенной игрой стала пентаго. В отличие от шахмат и го поисковое пространство игры небольшое, что позволяет современному компьютеру играть идеально: с учетом всех возможных симметрий количество возможных позиций в пентаго составляет 3 009 081 623 421 558. В течение нескольких часов суперкомпьютер Edison семейства Cray, находящийся в Национальном научно-вычислительном центре энергетических исследований (NERSC), нашел «сильное» решение игры. Программа использовала для вычислений 98 304 потоков.

Также удалось найти решение для такой необычной игры, как «Магараджа», где черные имеют набор обычных шахматных фигур, а белые — единственную фигуру Магараджа. Это ферзь, способный ходить как конь. Доказано, что черным гарантирована победа.

Американский математик и шашист Марион Франклин Тинсли был сильнейшим игроком мира в английские шашки на протяжении 30 лет. Тинсли ни разу в жизни не проигрывал матч за первенство мира и за свою 45-летнюю карьеру проиграл всего семь партий.
В 1992 г. проводился матч между Марионом Тинсли и программой «Чинук». Первый матч Тинсли выиграл у программы со счетом 4:2 при 33 ничьих. При анализе матча выяснилось, что в одной из партий Тинсли выбрал единственную верную позицию, ведущую к победе, за 64 хода до конца матча.
На матче реванше Тинсли успел сыграть шесть игр — все ничьи. После этого он почувствовал себя очень плохо и у него диагностировали рак поджелудочной железы и вскоре он умер. В 1995 г. программа «Чинук» выиграла у Дона Лафферти, наследника Тинсли на шашечном троне. Из 32 сыгранных партий единственная результативная партия завершилась в пользу компьютера. После этого первенство в шашках окончательно перешло к машинам.

Одна из величайших шахматных партий всех времен.
Более распиаренный матч, о котором слышали даже далекие от шашек и шахмат люди, состоялся в 1997 г. Гарри Каспаров проиграл суперкомпьютеру Deep Blue в матче из шести партий. Для сравнения: Deep Blue был способен просматривать 200 млн позиций в секунду, в то время как современные компьютеры просматривают 1—3 млн позиций в секунду. За прошедшие 20 лет компьютеры так и не смогли догнать этот уникальный инженерный проект.
Машина от компании IBM была не просто суперкомпьютером, а специализированным под шахматы проектом, в котором установили отдельные кристаллы с генераторами ходов, позволявшие за один такт процессора сгенерировать все возможные ходы в позиции. Однако сейчас такая мощь нам не требуется — мобильный телефон обыгрывает ведущих гроссмейстеров.
Огромный Deep Blue впечатлял одним своим видом, но его размеры привели к появлению стойкого мифа: мол, машины выигрывают у людей только благодаря своей мощности и быстроте — давят брутфорсом. Человек может просмотреть всего две или пять позиций в секунду, компьютер — сотни миллионов.

На самом деле это не так. На рисунке выше приведен пример задачи из учебника — мат в шесть ходов. Deep Blue, используя полный перебор, должен был бы потратить около 356 лет на поиск решения. В среднестатистической шахматной позиции возможно 35 ходов, чтобы просмотреть на два хода — 35 в квадрате, на три — в кубе и т.д.
Любая сильная современная программа находит решение на настольном компьютере максимум за несколько секунд. Более того, на современной машине вы можете запустить программу чемпиона 2008 г. против программы чемпиона 2015 г. Из 27 партий одну партию будет выигрывать слабейшая программа, 26 партий — сильнейшая. Это прогресс, достигнутый за семь лет. Это произошло не за счет роста мощности железа, а благодаря развитию алгоритмов. За данным процессом не стоят тысячи программистов и десятки гроссмейстеров. Сейчас над шахматными программами работают либо программисты-одиночки, либо очень небольшие группы. Например, одну из самых сильных программ в мире шахмат — Stockfish — создали три программиста. Над самыми крупными, с точки зрения числа задействованных программистов проектами — Deep Blue и Каисса — работало менее десятка программистов.
Все современные шахматные программы так или иначе являются детищем машинного обучения. В шахматной программе есть оценочная функция, рассматривающая позицию без всякого перебора. Это, грубо говоря, логистическая функция, имеющая 3—5 тыс. параметров, для подбора которых используются большие массивы шахматных позиций, выбранных обычно из партий самой же программы. Программа играет несколько тысяч партий, оттуда извлекаются позиции, программа снова играет и т.д. — цикл не заканчивается никогда.
Самое забавное, что если мы говорим о брутфорсе, то надо задаться вопросом: действительно ли брутфорс на стороне машин? В среднестатистическом человеческом мозге примерно 86 млрд нейронов и 150 трлн синапсов. Каждый синапс содержит примерно 1 тыс. молекулярных переключателей. Таким образом, если мы пересчитаем мозг в триггеры, то получим 150 квадриллионов (1,5×1017) триггеров транзисторов. Конечно же, это две «машины» с абсолютно разной архитектурой, но мы очень примерно можем сравнивать их на некоторых задачах.

Один из самых мощных на сегодняшний день процессоров (Sparc-M7) имеет 10 млрд транзисторов. Самая большая программируемая пользователем вентильная матрица (FPGA) содержит до 20 млрд транзисторов. Это всего 2×109 раз, а в мозге 1,5×1017 раз. Конечно, компьютеры имеют одно большое преимущество — скорость. Sparc работает на частоте 4,3 ГГц. Человек же имеет следующие потенциалы действия нервных клеток: амплитуда — около 0,1 В, длительность — около 1 мс, «рабочая» частота» — 10—100 Гц (до 1000 Гц).
Правильно сказать, что мозг до сих пор является брутфорс-решением, так как это гигантская нейронная сеть, которую мы пока не можем сэмулировать в реальном времени. Операции, которые мы проводим, играя в шахматы, совсем не похожи на простые арифметические. Если взять более сложную задачу, например, распознавание образов, то будет ясно, что машина не в состоянии выполнять необходимые расчеты так же быстро, как человеческий мозг.

В ИИ изначально было две крупных школы — «чистюль» и «грязнуль». «Чистюли» — по большей мере математики, настаивавшие, что должны использоваться корректные методы решения задач, имеющие формальное обоснование, или хотя бы обоснование статистическое.
«Грязнули» считали, что неважно, каким образом решать задачу. Если решение работает в рамках предметной области, значит оно хорошее. Они ввели термин hacking для ИИ — мы ломаем задачу, чтобы решить ее.
Если сейчас посмотреть на методы ИИ, используемые в играх, то увидим определенный синтетический подход. Формально необоснованные трюки, но хорошо работающие на практике, соседствуют с формально доказанными методами.
ИИ, как и большинство других наук, начинался с бионического подхода. Если в природе есть работающее решение, давайте для начала его скопируем, пока не придумали что-то более совершенное. Леонардо да Винчи первым придумал конструкции летательных аппаратов, изучая принцип полета птиц. Вполне естественно, что, столкнувшись с задачей создания систем, решающих интеллектуальные задачи, захотелось подсмотреть у природы, как это устроено. Мы ведь уверены, что наш собственный мозг работает.

Первыми создателями моделей математических процессов, происходящих в человеческом мозге, стали Уорен МакКалок, Уолтер Питтс, Дональд Хебб в 1940-х годах. Они придумали первую модель искусственного нейрона — простой логистический сумматор.
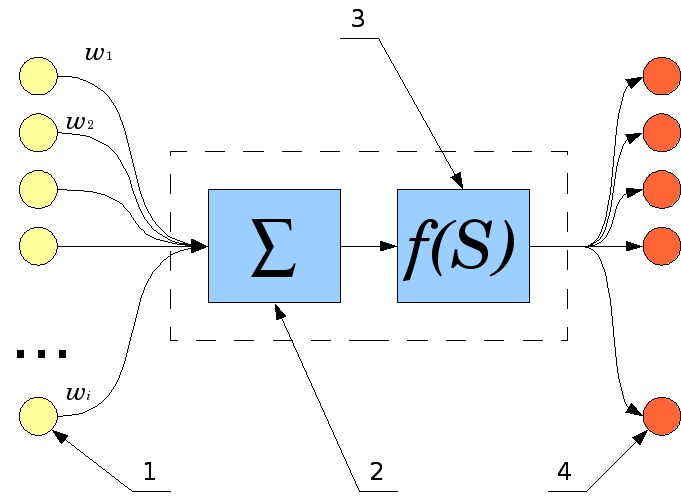
Схема искусственного нейрона:
- нейроны, выходные сигналы которых поступают на вход данному;
- сумматор входных сигналов;
- вычислитель передаточной функции;
- нейроны, на входы которых подается выходной сигнал данного;
- Wi — веса входных сигналов.
Во многом отношения между этими людьми заложили некоторые базовые вещи в науке. Например, мы не называем нейронные сети кибернетическими системами, хотя Мак
