Hex: Мастерим бота
 — Стало быть, эта штуковина только выглядит так, будто умеет думать? — Э… да.
— Стало быть, эта штуковина только выглядит так, будто умеет думать? — Э… да.
— А на самом деле не думает? — Э… нет.
— То есть просто создаёт впечатление, будто бы думает, а на самом деле это всё показуха?
— Э… да. — Ну точь-в-точь как все мы.
Терри Пратчетт «Санта-Хрякус»
Триумфальные победы AlphaGo (и впоследствии AlphaZero) всколыхнули интерес общественности как к нейросетям, так и к настольным играм. Конечно, есть люди, которые считают, что AlphaZero «побеждает нечестно», поскольку на самом деле учится не совсем с нуля, а использует поиск Монте-Карло, в дополнение к тому, что ему советует нейросеть (говоря серьёзно, использование языковых моделей, в применении к настольным играм, выглядит интригующим и я желаю всяческих успехов в этом направлении), но хочется поэкспериментировать с чем-то не требующим грандиозных вычислительных мощностей и получить на выходе что-то, пусть и не играющее «на уровне Бога», но вполне пригодное для того чтобы играть с ним было интересно.
Мне важен результат и я готов использовать минимакс, Монте-Карло или даже нейросети, лишь бы добиться хоть какого-то успеха (особенно с учётом некоторых ограничений накладываемых JavaScript на производительность, по сравнению с компилируемыми языками и массовым использованием GPU). Разумеется, начинать эксперименты с Го несколько самонадеянно. К счастью, это не проблема. Я знаю много других игр.
Игра «Гекс», независимо придуманная двумя известными математиками, Питом Хейном и Джоном Нэшем в 40-ых годах прошлого века, выглядит достойным кандидатом для экспериментов. Правила очень простые: игроки по очереди ставят по одному камню своего цвета на пустые поля доски. Для победы необходимо соединить противоположные стороны доски непрерывной цепочкой камней своего цвета. В целях компенсации преимущества первого хода, используется «правило пирога»: второй игрок может сменить цвет, сразу же после выполнения в игре самого первого хода.
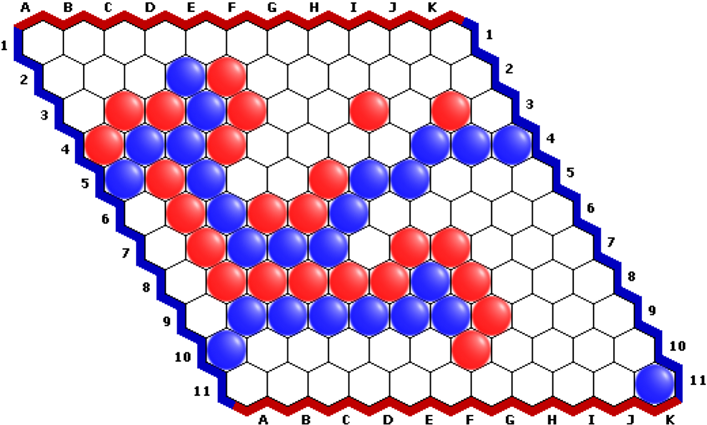
Эта игра словно предназначена для машинного обучения. Камни, поставленные на доску, впоследствии не перемещаются и не убираются с доски, что ограничивает максимальную продолжительность партии. Кроме того, довольно очевидно, что один из игроков обязательно победит, а поскольку цели игроков исключают друг друга, никакие ничьи в игре невозможны.
В то же время, тактика игры вовсе не тривиальна. Прежде всего, как и в Го, в Гексе существуют «хорошие формы». Речь идёт о неразрезаемости. Конечно, если мы играем вплотную, камень к камню, разрезать такое соединение нельзя, но соединяясь таким образом, мы продвигаемся по доске слишком медленно. При размещении камней по диагонали, продвижение идёт гораздо быстрее, без какого либо ущерба надёжности. Если удастся соединить неразрезаемыми формами обе свои стороны, мы победили!

Если конечно не забывать ставить камень в парную точку, при попытке разрезания формы противником. Соединение по диагонали («мост») самая простая и чаще всего используемая форма. Вообще же, известных форм довольно много. Кроме того, как показывает практика, в этой игре гораздо плодотворнее думать о том как не дать противнику соединиться, чем пытаться соединить свои стороны самому. Если удастся помешать победить противнику, победа никуда не уйдёт. Теперь, когда мы немного разобрались с тактикой, вот вам задачка от Камерона Брауна:
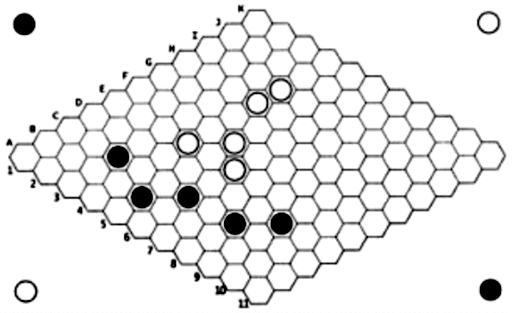
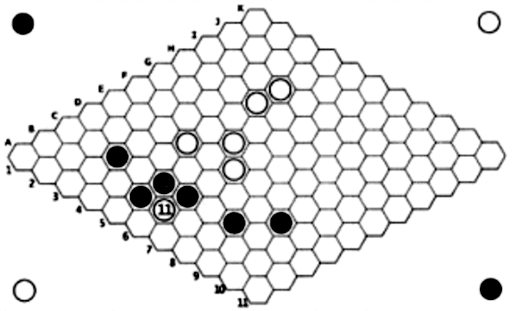
Начинаем с попытки разрезания моста (11). Чёрные отвечают вполне закономерно и ход может показаться бесполезным, но это не так.

Прорываемся сквозь строй белых (13). У чёрных есть отличный ответ и попытка была бы обречена на неудачу, если бы не предыдущий ход. Соединяемся (15):

и победа у белых в кармане…
Cтоит сказать о том, почему алгоритмы, столь хорошо зарекомендовавшие себя в Шахматах, для Гекса малоприменимы. Прежде всего, коэффициент ветвления дерева состояний в игре Гекс очень высок. Если в Шахматах, из начальной позиции, доступно всего 20 ходов, то в Гексе, на доске 11×11, их более сотни. Может показаться что разница не так велика, но при углублении перебора мы сталкиваемся со степенной функцией.
Вторая причина заключается в отсутствии удобной оценочной функции. В Шахматах, в первом приближении, оценка сводится к подсчёту материала (фигур на доске). Это очень быстро и хорошо работает, поскольку значение функции оценки монотонно и достаточно плавно увеличивается, по мере приближения игрока к победе. В Гексе, как и в Го, отдельные камни на доске не имеют значения. Важно их взаимное расположение. В результате, поскольку у нас нет оценочной функции, мы не можем останавливать перебор на какой-то фиксированной глубине, как это делается в шахматных алгоритмах.
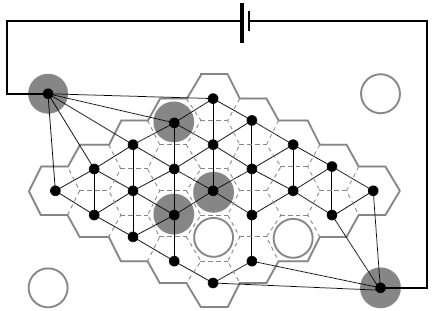
Я экспериментировал с этим, вычисляя максимальный поток в графе. К сожалению, успеха на этом направлении добиться не удалось. Такая оценка ресурсозатратна сама по себе, а высокий коэффициент ветвления буквально свёл на нет все усилия. За 10 секунд перебора мне удавалось углубиться всего на 2 полухода, чего совершенно недостаточно для того чтобы начали работать какие либо оптимизации альфа-бета отсечения. Возможно это работало бы в нейтивных сборках на C++, но для JavaScript этот путь, по всей видимости, закрыт.
К счастью, при использовании метода Монте-Карло, этого и не требуется. Суть подхода заключается в том, что симуляция игры каждый раз ведётся до победы одного из игроков. При этом, все допустимые ходы из начальной позиции и все ответы противника проверяются полностью, а последующие ходы выбираются случайно. Количество просмотров и количество побед для каждого хода из начальной позиции фиксируются. Очевидно, что при таком подходе вычислять оценочную функцию не требуется, но возникает другой вопрос: в соответствии с каким критерием выбирать начальные ходы, чтобы максимально исследовать наилучшие ходы, с одной стороны и при этом не забывать о всех остальных ходах? Решению этого вопроса посвящена знаменитая «задача о многоруком бандите».

Здесь w[i] — количество побед при выборе i-го хода, n[i] — количество проверок хода, а N — общее количество симуляций. Коэффициент c подбирается экспериментально и определяет насколько значима разведка ещё не исследованных ходов по сравнению с более глубоким исследованием ходов, обеспечивающих большее количество побед. По завершении всех симуляций (или когда закончится время на обдумывание хода) выбирается ход с наибольшим количеством проверок (ход с наибольшим количеством побед может оказаться просто недостаточно исследованным). Можно ли как-то улучшить этот алгоритм? Конечно.
Далее, мы можем захотеть сделать игру нашего бота более похожей на то, как играют люди. Это просто — надо взять достаточно большую базу данных игр людей друг с другом, и обучить нейросеть на её основе. Обученная модель будет предсказывать наиболее вероятные ходы из той или иной позиции. Полученные вероятности Q[i] называются априорными. Просто добавим их к нашему критерию выбора в качестве дополнительного слагаемого, не забыв поделить на N, для того чтобы обеспечить уменьшение их влияния, по мере получения результатов симуляций.

Архитектура модели почерпнута из замечательной книги, посвященной использованию нейросетей в применении к игре Го. Несколько свёрточных слоёв определяют наличие на доске базовых паттернов, после чего плотные слои формируют матрицу априорных вероятностей для возможных ходов. Поскольку речь идёт о вероятностях и выборе одного хода из нескольких возможных, softmax используется в качестве функции активации в последнем слое, а categoricalCrossentropy определяет функцию потерь. Функция активации relu, в промежуточных слоях, помогает бороться с возможными проблемами переобучения посредством регуляризации.
Потребовалось несколько суток для получения исходных данных, после чего выяснилось, что подавляющее число игр велось на доске 10×10. Впрочем, 15255 игр, для первичного обучения модели, оказалось вполне достаточно. Ещё один важный момент: данные для обучения крайне желательно перемешивать таким образом, чтобы позиции относящиеся к одной и той же игре не следовали друг за другом (и не попадали таким образом в один пакет обучения). Всякого рода сортировками я предпочитаю заниматься внутри базы данных. Просто выгружаем результат разбора игр, добавляя к каждой строке случайное число, потом сортируем и выгружаем в csv для последующего обучения.
BbFeDfChEgEhGgGhHhFgGeHgDhCjDiDjEiHcEdFbDcDbEb
Каждая пара символов определяет очередной ход. Первая буква задаёт столбец, вторая строку (мне пришлось потратить некоторое количество времени чтобы выяснить это). Этот формат данных также был расширен. Мне понадобилось хранить оценку позиции на момент выполнения хода (ниже я расскажу, для чего это понадобилось). Поскольку это число из интервала (-1, 1), достаточно записывать знак и несколько цифр после десятичной точки. В результате получилось что-то в этом духе:
Eb-08FgHf03GhHh03GiHi03HgIg03CiGe03IfEf03DhJf-JeKd03KeGd03BjEg03EhFh03GgCh03JcAj03Ak
Вас может сбить с толку, что числа записаны не перед каждой парой символов, но этому есть простое объяснение. Оценку позиции в этой игре производил только второй игрок.
Есть ещё кое что важное, о чём стоит упомянуть. В какой-то момент бот начал вести себя странно. Он выигрывал, но делал это не благодаря, а скорее вопреки своим ходам. Вообще, складывалось впечатление, что бот пытается соединить верх и низ доски, пытаясь играть за первого, а не за второго игрока. Попытки исправить это продолжались довольно долго, пока я не понял, что чтобы не путать себя и бота, любую позицию следует рассматривать с точки зрения первого игрока, при необходимости отразив доску относительно главной диагонали. Это всё сильно упростило и дело пошло на лад.
Если отражение доски использовалось как при обучении модели так и в ходе работы бота, то поворот доски имел отношение только к процессу обучения. Когда я работал с уже обученной моделью для игры Го, то заметил, что рекомендуемые ей ходы не симметричны. Так первый ход всегда выполнялся в пункт 4–4 в правый верхний угол (понятно, что начальные ходы в остальные три угла совершенно равноценны). В тот момент (поскольку модель была уже обучена), я заменил один вызов predict шестнадцатью, восемь раз повернув и отразив доску и изменив цвет камней (лучший ход противника — это и твой лучший ход), но более правильным решением было бы добавление всех этих отражений и поворотов в обучающую выборку. При обработке изображений, такая операция называется обогащением исходных данных. В случае Гекса, доска более хитрая и достаточно всего одного поворота (относительно центра доски).
Технология разработки бота для DagazServer была уже отработана ранее. Полученный в результате бот играет в Гекс довольно неплохо, но сила его игры зависит, в первую очередь, от качества обучения модели. Обучение с учителем — это только первый шаг, поскольку не позволяет играть лучше тех людей, игры которых составили обучающую выборку. Чтобы двигаться дальше, требуется ещё один инструмент, позволяющий боту играть самому с собой или с другой версией бота.
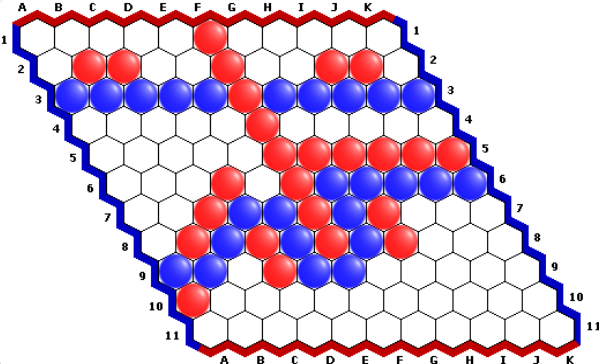
Серьёзно, кто-то практиковался в абстрактном искусстве, а в результате игра попала в обучающие данные. Чему хорошему может научиться модель на таких примерах? К сожалению, данных действительно очень много и совершенно невозможно проверить их все вручную. Но мы всегда можем получить новые данные, заставив бота играть самого с собой.
Это одно из назначений HexAuto. Другое его применение заключается в том, что мы можем автоматизировать сравнение силы различных ботов по итогом серий их игр друг с другом. Победы в одной игре недостаточно для того чтобы определить что один бот сильнее другого. Слабый бот мог победить вследствие случайного стечения обстоятельств. Для более корректной оценки используется биномиальный тест.
>>> from scipy.stats import binom_test
>>> binom_test(51, 100, 0.5)
0.9204107626128211
>>> binom_test(60, 100, 0.5)
0.056887933640980784
Если один бот победил другого 51 раз в серии из 100 игр, можно сделать вывод от том, что они равны по силе (0.5) с вероятностью 92%. Если же побед было 60, равенство ботов по силе маловероятно (5%). Нам необходимо большое количество игр, как для дообучения модели, так и для сравнительной оценки ботов. Насколько качественно будут играть боты зависит от выбранного алгоритма. Можно просто семплировать вероятности предсказанных ходов (что будет работать экстремально быстро), либо запустить полноценный MCTS, используя вероятности полученные от модели в качестве априорных. Разница очевидна:
Won [1]: Fc03GfFg03HdGh448IdHc03AfEf03AkJb03JdBi999HfIg999DeCj991ChBg03GgFh330JjBh03AdKc03BdBa553IcIb666GiDd03BkCc03IfBe03CdDc03CeCk03AeHh03FaBb03EhJg03AjCi03EkKf03AiAh03EdKd03EcFe03BcKb03GbCb03CaFd03AgGc03GeDa03GjCf03BfGa03FbDh03EgDg03CgFf03DfDj03HiFi03FjKh03AbAc03AaJi03DkHg03HkIk03KiIj03HjEi03DiEj03HbIa
o * o * . o * . * . .
o * * . . o o o * * *
* o * * o * * * o . *
o o o * o * . o o o *
o * o o . * o . . . .
o o * o * * o o o . *
o * o * o * o * * * .
* * o * o * * * . . *
o * * o * * o o . * o
o . * * * o o o * o .
o o * o o . . o * . .
FEN: aAaA1aA1A2/aB2cC/AaBaCa1A/cAaA1cA/aAb1Aa4/bAaBc1A/aAaAaAaC1/BaAaC2A/aBaBb1Aa/a1CcAa1/bAb2aA2-w
Total: 9/1 (10), time = 23.952Lose [2]:Hc03IiFf445EhDg03CiGg03FhHh03GiGj03HiJh03JiGh03FiKi03KhBi03BjAk03AjDi03Dh
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . * . . .
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . * . . . . .
. . . * . . * . . . .
. . . o o o * * . * o
. * o * . o o o o o *
o o . . . . * . . . .
* . . . . . . . . . .
FEN: 92/92/7A3/92/92/5A5/3A2A4/3cB1Aa/1AaA1eA/b4A4/A91-w
Total: 2/8 (10), time = 1773.71
В 77 раз медленнее, но зато гораздо осмысленнее! Кстати, обратите внимание: модели в этих двух прогонах использовались одни и те же, но при использовании sample-ai уверено лидировал первый игрок, в то время как для mcts-ai вторая модель подошла гораздо лучше. Объяснением этому может быть то, что вторая модель менее обучена и предоставляет MCTS большую свободу в выборе хода. В любом случае, достаточно очевидно, что обучать модель следует с учётом того как она будет использоваться. То что хорошо подходит для простого алгоритма, может оказаться неподходящим для более продвинутого.
Как бы там ни было, теперь у нас имеется потенциально бесконечный источник качественных данных. Каким образом это использовать? От «обучения с учителем» можно перейти к «обучению с подкреплением». По завершении игры, мы знаем кто из игроков победил. Это означает, что можно формировать обучающие данные таким образом, чтобы подкрепить ходы победителя и сделать менее вероятными выбор ходов ведущих к поражению. REINFORCE именно об этом.
Однако, здесь есть одна проблема: не все ходы выполненные в ходе игры вносят равноценный вклад в достижение победы. Подкрепляя слабые ходы мы можем не только затянуть процесс обучения, но и научить модель плохому. Интуитивно понятно, что ход «переломивший игру», выполненный из проигрышного положения, намного ценнее обычного тихого хода из позиции, в которой игроку ничего не угрожает, но как это формализовать? Мне нравится метод «актор-критик», формирующий подкрепление в зависимости от оценки позиции, с точки зрения игрока. Откуда взять оценку? У нас есть нейросеть, вот пусть она и считает!

Здесь, помимо выхода политики, добавлен дополнительный выход оценки (для чего пришлось перейти от последовательного API к функциональному). Подкрепление каждого хода формируется как R-E (где R означает награду — 1 у победителя и -1 у проигравшего, а E — оценку текущей позиции с точки зрения игрока). Поскольку выход оценки — непрерывное вещественное значение, в качестве функции потерь берётся mse, а tanh используется как функция активации в последнем слое.
В своей книге, Max Pumperla и Kevin Ferguson утверждают, что при использовании в качестве функции потерь categoricalCrossentropy, изменение знака подкрепления приводит к обращению вектора градиента политики, что даёт возможность уменьшать вероятность не успешных ходов. К сожалению, как только я передаю на выход политики отрицательные значения подкрепления, всё сразу же ломается: значения функции потерь уходят в отрицательную область (чего быть не должно) и обучение уже больше никуда не идёт. Возможно, знающие люди подскажут в чём тут дело.
Настройка обучения с подкреплением имеет свою специфику. Как правило, такие модели обучаются «с нуля» и качество обучающих данных, по крайней мере в начале процесса обучения, далеко от идеального (а по правде сказать, близко к рандомному). По этой причине, к таким данным следует относиться с крайней осторожностью. Не следует использовать такие данные повторно, устанавливая количество эпох больше 1, а размер пакета следует выбирать побольше (например 1024), чтобы как-то сгладить возможные огрехи в обучающих данных.
Также, при обучении с подкреплением, не следует использовать адаптивные алгоритмы оптимизации, такие как adagrad или adam, отдав предпочтение старому доброму стохастическому градиенту. Скоростью обучения рекомендуется управлять вручную, задавая в начале малые значения (~0.001) и постепенно увеличивая по мере необходимости. Это может помочь не пролетать мимо минимума функции потерь в процессе обучения.
За 20 суток непрерывной работы HexAuto получил около 10000 качественных партий в Гекс (как я уже говорил, MCTS-бот работает не быстро). Осталось понять, что с этим делать. Можно было бы запустить дообучение исходной модели, но у меня возникла идея получше. Обучение новой модели «с нуля», на новых исходных данных, позволит оставить за скобками все те странные игры, попавшие в первоначальную обучающую выборку по недоразумению (без кропотливой ручной проверки более чем 15000 партий). Это данные, в которых я уверен.
Кроме того, помните я говорил, что обучение с учителем не позволяет научить модель играть лучше чем худший из игроков в обучающей выборке? Так оно и было бы, используй бот рекомендации нейросети напрямую, но в нашем случае основную работу выполняет MCTS, а нейросеть просто даёт ему подсказки. Из этого следует, что мы можем получить новый опыт из игр MCTS-бота и использовать его для лучшего обучения модели.
Вы можете сами увидеть, насколько хорошо играет бот, зарегистрировавшись на DagazServer (регистрация бесплатная и не требует ввода персональных данных). Если же вариант с регистрацией вас решительно не устраивает, можно посмотреть на версию игры на GitHub Pages. Должен предупредить, что в этом случае взаимодействие с ботом более опосредованное и иногда «виснет» (перезагрузка страницы по F5 в таких случаях обычно помогает). Обратите внимание на подсветку рекомендуемых ходов на доске (это просто рекомендация модели, MCTS не задействован). На текущий момент, мне удаётся его обыгрывать (особенно когда я не зеваю), но я всерьёз рассчитываю на то, что дальнейшее обучение позволит значительно улучшить качество игры.
