Графические модели на основе гауссовых копул
Частичная корреляция и условная независимость
В одной из прошлых статей, в которой шла речь о лог-линейных моделях и марковских сетях, был рассмотрен шутливый пример о зависимости между размером обуви человека и его математическими способностями. Статистические тесты говорят о том, что, как правило, у людей с бОльшим размером обуви выше математические способности.
Рассмотрим реальный пример — исследование «индекс удовлетворенности европейских клиентов рынком услуг мобильной связи» за 2005 год. Данные доступны в пакете semPLS среды R. Каждая переменная опроса представляет рейтинг со шкалой от 1 до 10. Из этих данных мы рассмотрим только три переменные — оценка мобильного провайдера при его рекомендации друзьям или коллегам (Recommendation); оценка обоснованности платы за услуги (Fair Price); оценка качества услуг предоставляемых мобильным оператором (Overall Quality). Сводка результатов опроса по этим переменным показана ниже.
Для оценки степени ассоциации между переменными Recommendation и Fair Price используем коэффициент корреляции Спирмена. Он получается достаточно большим.
Если рассматривать все три переменные в совокупности и находить их частичные корреляции — попарные коэффициенты корреляции с учетом влияния третьей переменной, результат получается иным.
Обратите внимание, коэффициент корреляции между переменными Recommendation и Fair Price, с учетом влияния переменной Overall Quality, оказался очень малым. Парная корреляция между этими переменными равная 0,4 уменьшилась, в случае частичной корреляции между ними, до 0,02.
Полученная выше матрица определяет следующий граф с весами ребер равными коэффициентам частичных корреляций
Но …
Все казалось бы хорошо, однако, нулевой (или близкий к нулю) коэффициент частичной корреляции между случайными величинами, в общем случае, не указывает на то, что эти случайные величины условно независимы. Тем не менее, это свойство справедливо для многомерных нормально распределенных случайных величин. То есть две одномерные случайные величины из распределения
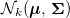условно независимы тогда и только тогда, когда их коэффициент частичной корреляции равен нулю. Равенство нулю (i, j) коэффициента частичной корреляции эквивалентно равенству нулю (i, j) элемента матрицы обратной к 
. Оценка матрицы 
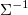, точнее ее разреженной формы, является основным объектом моделирования в задачах построения гауссовых графических моделей (gaussian graphical models / gaussian markov random fields).Немного о копулах
Прежде чем говорить о гауссовых копулах пару слов об общей конструкции.
Допустим есть набор совокупного наблюдения нескольких переменных (случайных величин). Функции распределения каждой из этих случайных величин в отдельности — одномерные маргинальные распределения, ничего не говорят о взаимосвязях между переменными. Эту информацию определяет совместное распределение случайных величин.
Копула — функция, связывающая совместное распределение случайных величин и их маргинальные распределения (здесь и далее всюду подразумеваются только одномерные маргинальные распределения). С точным определением на русском языке можно ознакомиться в работе [1]. В чем привлекательность копул? Процитирую [1]: «Копула-функции дают возможность разделить описание распределения случайного вектора на две части: частные распределения компонент и структура их зависимостей.»
Если некоторые из маргинальных распределений копулы дискретны, то в оценке такой копулы возникают определенные сложности. Причина этой ситуации в отсутствии взаимно-однозначного соответствия между областью значений k маргинальных случайных величин и областью определения копулы — гиперкубом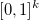 
. Подробности можно найти, например, в обзоре [2].
Гауссова копула
Гауссова копула имеет вид
где
— функция k-мерного нормального распределения с нулевым вектором средних и корреляционной матрицей , 
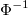— квантиль-функция стандартного нормального распределения. В этой формуле выполняется двойное преобразование переменных. Пусть 
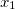наблюдаемое значение случайной величины по первой координате, а 
— маргинальная функция распределения (cdf) этой случайной величины. Тогда полагаем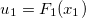 
и получаем значение 
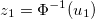латентной переменной первой координаты k-мерного распределения Гаусса.В статье [3] детально рассмотрены несколько примеров гауссовых копул как с непрерывными, так и с дискретными маргинальными случайными величинами. Вообще, гауссовы копулы не стоит воспринимать исключительно в контексте инструмента для марковских сетей. Как можно видеть из работы Данахера и Смита, это также методы построения моделей покупательской активности и нахождение распределения охвата (Reach distribution) рекламной кампании в СМИ и ряд других моделей совместного распределения случайных величин. Разбор одного из этих примеров с кодом на R можно найти ниже под спойлером.
require(MM) # to load the example data
data(danaher)
# define data sample corresponding to the contingency table
df.danaher<-data.frame( bacon=rep(0:4,rowSums(danaher)),
eggs=unlist(apply( danaher, 1, function(x) rep(0:4, x) )) )
# fit the gaussian copula
require(sbgcop)
fit <- sbgcop.mcmc(df.danaher, nsamp = 5000, odens = 1, seed = 1, verb = F)
# estimate the correlation matrix
burn.in <- 500
Sigma <- apply(fit$C.psamp[,,-c(1:burn.in)], c(1,2), median)
# find the fitted results
n <- nrow(danaher)
N <- sum(danaher)
eggs.cum.sum <- cumsum( colSums(danaher)/N )
bacon.cum.sum <- cumsum( rowSums(danaher)/N )
eggs.norm.limits <- qnorm( c(0, eggs.cum.sum) )
bacon.norm.limits <- qnorm( c(0, bacon.cum.sum) )
lower.limits <- as.matrix( expand.grid(head(eggs.norm.limits, n),
head(bacon.norm.limits, n)) )
upper.limits <- as.matrix( expand.grid(tail(eggs.norm.limits, n),
tail(bacon.norm.limits, n)) )
require(mvtnorm) # to the distribution function of the multivariate normal distribution
fitted.results <- sapply(1:n^2, function(i)
pmvnorm(lower.limits[i,], upper.limits[i,], corr = Sigma)*N)
fitted.results <- matrix(fitted.results, nrow = 5, byrow = T)
dimnames(fitted.results) <- list(bacon = as.character(0:4),
eggs = as.character(0:4))
# Estimated correlation matrix of the gaussian copula
Sigma
# Input data
danaher
# Fitted results
fitted.results
# Mosaic plots of the input data and fitted results
par(mfrow = c(1,2))
mosaicplot(t(danaher), main = "Input data", color = "royalblue")
mosaicplot(t(fitted.results), main = "Fitted results", color = "royalblue")
Результаты:
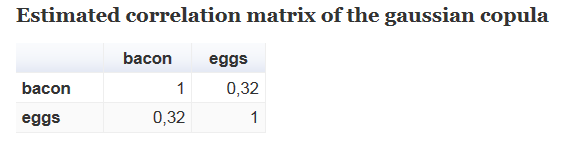
Получаем достаточно большой положительный коэффициент корреляции между числом покупок яиц и бекона. Теперь сравним исходные цифры с результатами полученными моделированием гауссовой копулой
На снимке выше таблица слева — входные данные с результатами опроса покупателей; таблица справа — результаты получаемые моделированием входных данных гауссовой копулой. Например, среди всех 548 опрощенных респондентов 16 (2,9%) покупали бекон 1 раз и яйца 2 раза. Модель оценивает число таких покупателей в 15,18 (2,8%).
Мозаичные графики таблиц
Оценка параметров графической модели гауссовой копулы
Задачу об оценке параметров GCGM можно условно разделить на две части — нахождение корреляционной матрицы гауссовой копулы и получение из нее разреженной матрицы для графического представления.Как и прежде, будем рассматривать метод применительно к данным опросов. Одна из особенностей таких данных — использование весов. Поэтому, в общем случае, требуется учесть веса выборки при оценках параметров модели.
Оценка корреляционной матрицы гауссовой копулы
Существует несколько методов оценки гауссовых копул с дискретными (или с дискретными и непрерывными) маргинальными распределениями. Один из них предложен Хоффом в работе [4] и реализован им в R библиотеке sbgcop. Этот алгоритм можно адаптировать ко взвешенным данным, учитывая веса выборки при определении ранговых маргинальных эмпирических функций распределения.
Получение разреженной матрицы графической модели гауссовой копулы
Здесь тоже есть простор для выбора. Когда получена корреляционная матрица гауссовой копулы можно воспользоваться классическим алгоритмом библиотеки glasso, основанным на статье [5]. Другой подход предложен в работе [6] и реализован авторами в R библиотеке BDgraph. Этот метод предполагает совместную оценку обоих матриц — корреляционной матрицы гауссовой копулы и разреженной матрицы графической модели на каждом шаге итерации алгоритма.
Комментарии к библиотекам sbgcop (v. 0.975) и BDgraph (v. 2.27)
Первая библиотека написана целиком на R и содержит несколько вложенных for-циклов. То есть вычисления организованы неэффективно. Кроме того, сэмплирование из усеченного нормального распределения реализовано численно неустойчиво — методом Inverse Transform. При определенных условиях, весьма вероятных в практическом применении, вместо сэмплируемого значения можно получить Inf.
Большая часть второй библиотеки написана на C++, куда перенесены, в частности, все for-циклы из sbgcop. Линейная алгебра написана с использованием Fortran. Проблема с сэмплированием из усеченного нормального распределения актуальна и в этом пакете.
Пример использования GCGM
Графические модели на основе гауссовых копул возможно использовать с разнообразными данными — маркетинговыми, социологическими, биологическими и многими другими. Здесь мы рассмотрим данные европейского социального исследования за 2012 год — ESS Round 6 European Social Survey Round 6 Data (data file edition 2.2), которые находятся в свободном доступе (ссылка). Из этих данных выбираем только респондентов из России. В блоке «Политика» этого опроса представлены следующие 5 оценочных суждений о степени доверия различным политическим органам и институтам власти
где шкала варьируется от 0 = No trust at all до 10 = Complete trust.
Дополним этот набор величин следующими четырьмя переменными:
- «How interested in politics» c 4 категориями (1 — Not at all interested, …, 4 — Very interested);
- «Did you vote in the last national election?» c 2 категориями (1 — Yes, 2 — No), вопрос относился к голосованию на выборах в Государственную думу РФ в 2011 году;
- «gender» (1 — Male, 2 — Female)
- «education» с 11 категориями (1- No primary, …, 11 — Ph.D.).
Мы отбираем респондентов возрастом от 23 лет, у которых нет пропущенных значений в ответах на все рассматриваемые вопросы. В модели также используются веса респондентов исследования — design weight.
Для построения графа модели доступно решение из коробки — функция qgraph одноименной библиотеки строит изображение графической модели определяемой матрицей частичных корреляций. Более гибкого и наглядного решения можно достичь используя R пакеты visNetwork (использует JS библотеку vis.js) и shiny. Первый пакет выполняет построение графа модели, второй дополняет возможность настройки уровня разреженности модели 'на лету'.
Картинка кликабельна, ссылка ведет к html файлу с графом модели.
Здесь Normalized Sparsity Level отвечает за значение коэффициента перед L1 нормой штрафной функции задачи graphical lasso (эти величины нормированы таким образом, что минимальное значение коэффициента, при котором граф модели не содержит ребер, полагается равным 1). Второй управляющий параметр — Absolute Correlation Level, скрывает ребра между вершинами, у которых коэффициенты частичной корреляции по абсолютной величине меньше заданного значения.
На снимке с графом подсвечено значение веса ребра между вершинами voted (1 — голосовал, 2 — нет) и interested in politics (1 — совсем нет, …, 4 — определенно да). Это значение, равное -0.34, показывает достаточно сильный уровень ассоциации между заинтересованностью политикой и готовностью голосовать на выборах, что вполне ожидаемо.
Еще одна картинка
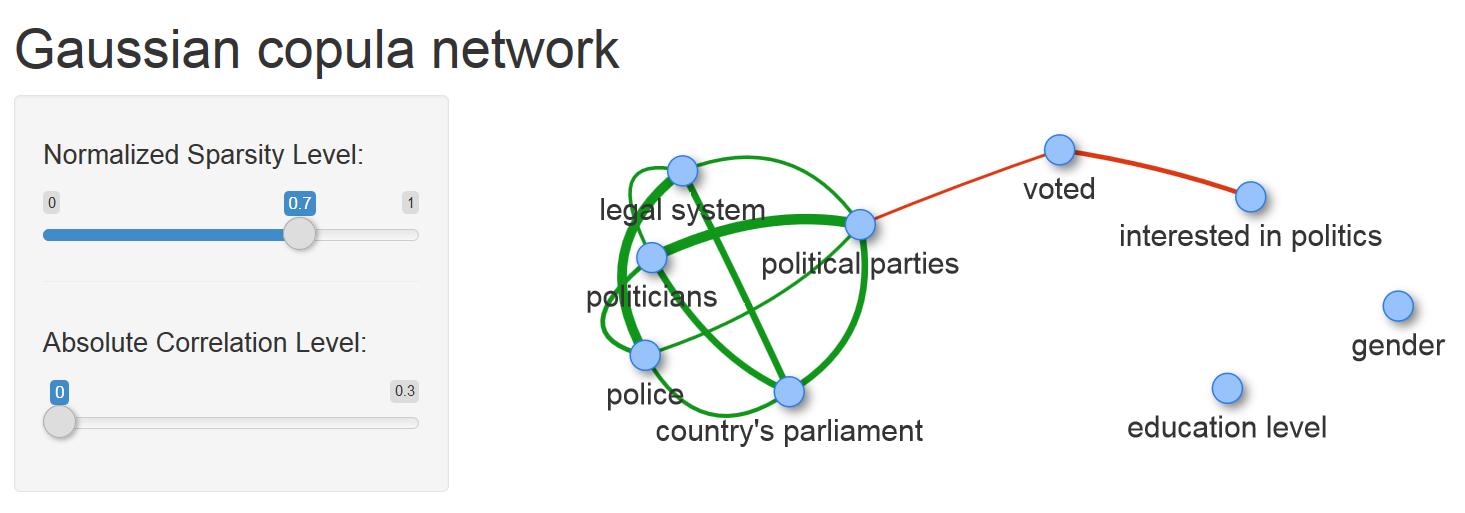
Что показывает модель?
Полагаю, наиболее важной частью этой модели является ребро соединяющее вершины voted и political parties. Оно единственное соединяет две компоненты графа и решение об участии в голосовании на выборах непосредственно зависит только от одной переменной доверия — доверия к политическим партиям. Все остальные переменные доверия условно независимы с переменной voted. Поэтому среди рассматриваемых переменных эта связка является ключевым фактором взаимодействия граждан и государства.
Отбор переменных для построения GCGM
Далеко не во всех случаях есть априорный выбор набора переменных для построения модели. Если представляет интерес построение GCGM, в граф которой будет включена какая-либо определенная переменная, то какие дополнительные переменные должны быть отобраны для анализа?
Слишком большому числу входных переменных для GCGM сопутствуют две проблемы. Во-первых, нахождение параметров гауссовой копулы для дискретных данных является трудоемким вычислительным процессом. Мощности лэптопа для решения задачи с большим числом переменных за приемлемое время будет недостаточно. Во-вторых, понимание графа с большим числом переменных, пусть и разреженного, будет затруднено (например, могут «мешать» сильные связи каких-либо переменных, которые совершенно неинтересны в контексте рассматриваемой задачи).
Подходящим решением вопроса по отбору переменных в GCGM для заданной переменной является построение минимального дерева взаимной информации (дерево Chow-Liu). Это быстрый алгоритм, описание которого в этой публикации не входит в мои планы. Детали можно найти в статье [7]. Структурное свойство дерева Chow-Liu, нестрого говоря, состоит в следующем — чем ближе между собой две вершины в этом дереве, тем они «более зависимы». Поэтому находим в дереве целевую переменную, определяемся с радиусом и выбираем все подходящие вершины этого дерева. Пример ниже построен для целевой переменной «В России политические партии предлагают избирателям по-настоящему разные программы», со шкалой ответов от 0 до 10. Дерево из примера было построено с использованием R библиотеки NetworkD3 (создает ряд d3.js графиков).
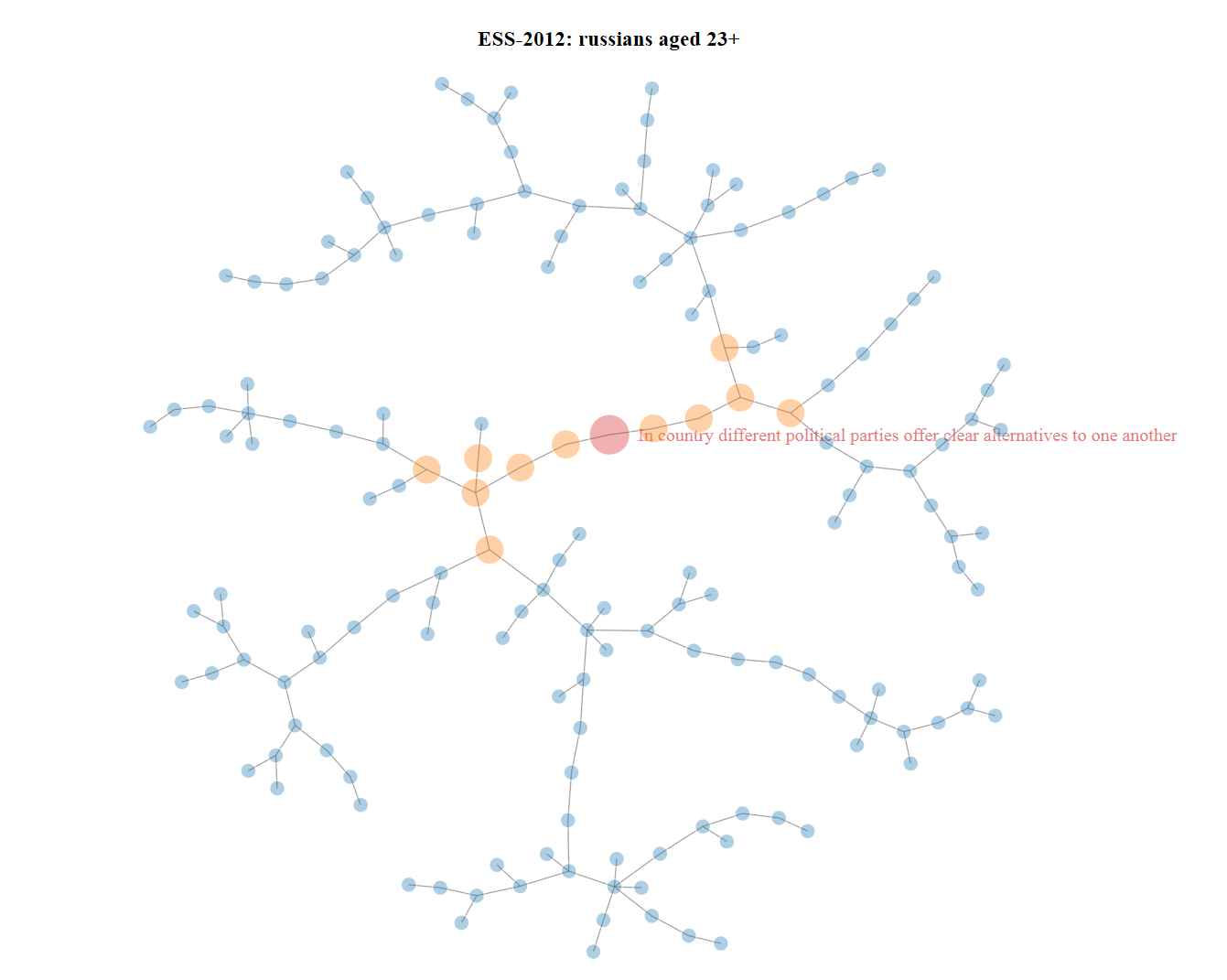
Картинка кликабельна, ссылка ведет к html файлу.
Резюме
Метод GCGM, дополненный алгоритмом предварительного отбора переменных, позволяет быстро, легко и содержательно анализировать структуры зависимостей в данных, выделяя в них ключевые связи.
Литература
[1] Д. Фантаццини (2011) Моделирование многомерных распределений с использованием копула-функций. I, Прикладная эконометрика, 2 (22), 98 — 134.
[2] C. Genest and J. Nešlehová (2007) A Primer on Copulas for Count Data, ASTIN Bulletin, 37(2), pp. 475–515.
[3] P.J. Danaher and M.S. Smith (2011) Modeling Multivariate Distributions Using Copulas: Applications in Marketing, Marketing Science 30(1), pp. 4–21.
[4] P.D. Hoff (2007) Extending the rank likelihood for semiparametric copula estimation, Ann. Appl. Stat., 1, pp. 265–283.
[5] J. Friedman, T. Hastie and R. Tibshirani (2008) Sparse inverse covariance estimation with the lasso, Biostatistics, 9(3), pp. 432–441
[6] A. Mohammadi and E.C. Wit (2015) Bayesian Structure Learning in Sparse Gaussian Graphical Models, Bayesian Anal. 10(1), pp. 109–138.
[7] D. Edwards, G.C. G de Abreu and R. Labouriau (2010). Selecting high- dimensional mixed graphical models using minimal AIC or BIC forests. BMC Bioinformatics, 11:18.
