Гипотеза Эскобара21.11.2022 20:46

Эскобар — великий математик, живший на Земле на прошлом витке общемирового времени.

На прошлом витке чего-о?

Изобрёл плоскостные числа — у нас они называются комплексными. Выдвинул гипотезу о знаке, что числа могут быть не только положительными и отрицательными, но и ещё, подобно тому как можно двигаться на плоскости не только вперёд и назад, но и вправо и влево — числа тоже могут быть расположены в других направлениях. В конце своей жизни Эскобар разочаровался в математике, да и вообще во всём. И в нашем витке времени он стал музыкантом. И никто бы не узнал, что он в душе математик, если бы на одном из концертов у него не взяли интервью, где в ответ на предложение сравнить два варианта он категорически выдал свою гипотезу за аксиому: двух вариантов недостаточно.

Комплексные числа были открыты без участия Эскобара, но это не значит, что мы должны отказываться от его наследия. Все знают, что 2+2=4, 2×2=4, 2^2=4. Только, при возведении в степень существует разница в порядке аргументов. Что если применить гипотезу Эскобара на нашем убеждении, что у порядка при возведении в степень может быть только два варианта? Ну, а вдруг — больше?

Степень

Тексты у нас чисто сугубо психологические и возникают спонтанно.

Люди давно знали что такое степень. Ещё бы, замена произведения чисел на сложение степеней превращает сложную операцию в лёгкую. Дело остаётся за малым: быстро переводить из числа в степень и обратно. Пришлось изобретать логарифм.

Смущало только два момента: что у нуля степень уходит в минус бесконечность, а у единицы степень равна нулю. Поэтому ноль так долго не хотели открывать, а единицу так вообще за число не считали. Но ведь отрицательные числа и отрицательные степени положительных чисел меньше единицы вполне согласованы, в чём дело?

Опасность проявлялось в том что умножение на ноль на уровне степеней уменьшала любую степень до бесконечно отрицательной. И что самое горькое: её нельзя вернуть обратно. Делить ноль на ноль это все равно что говорить: «не знаю». Надо было бы как-то постараться заранее сделать резервную копию того что вы собираетесь на ноль умножить, и не терять.

Это не единственная потеря в математике. Умножение числа на себя это всё равно что возводить число во вторую степень. Вернуть обратно число можно, вычислив корень, как степень одна вторая. Но отрицательные числа в квадрате будут положительными, и если возвращать обратно, то нужно кое-что постараться вспомнить о числе, то что потерялось, знак.

В целом, это не проблема — всего два варианта. Но, что если кроме положительных и отрицательных чисел есть и такие числа, которые в квадрате дают отрицательные? Знак-то, может, и теряется, но — тот который был, а не тот который стал.

Точки на плоскости намекают: поворот может быть степенью, увеличить степень в два раза может быть просто удвоенным поворотом. А значит, такие числа не только существуют, вторая составляющая это полноценный дубль первой составляющей, и у них прекрасная связь.

И конечно же, при вычислении корня таких комплексных чисел ровно два, знак теряется точно так же.

Так как аналогия с поворотом проста, то спокойно можно возводить любое комплексное число в любое комплексное число. Только, поворот имеет свойство повторять на следующих оборотах то же что было на предыдущих, и поэтому теряться может гораздо больше, чем просто знак. И если показатель у степени обратный, то происходит и ещё кое-что обратное: значение придётся восстанавливать.

Например, если минус один возвести в степень $e$ , а затем попробовать вычислить корень степени $e$ , то из-за потери одного оборота основным значением будет не минус один. И останется вопрос, а точно ли во время этих вычислений потерялся один оборот? Если количество потерялось, тогда каким точно оно было — не знаешь. И тогда ответом может быть любое число с модулем один. Особенно, если количество потерянных оборотов может быть напрямую бесконечным.

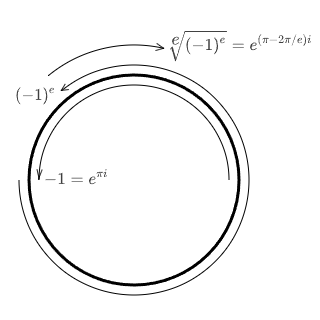
Место на плоскости может быть задано через два действительных числа. Но эти два числа могут означать не только шаги вправо и вверх, можно выбрать любые два различных направления и пересчитывать координаты из одной системы отсчёта в другую. При выделении «пересчётов» координат в «величины» возникло замечательное удобство: умножил — значит пересчитал. Так появились матрицы, двумерные сетки чисел. И вектора, как матрицы с единичной размерностью по одному из направлений.

Матрицы

Это не есть, так сказать, музыка.

Пересчёт набора координат в другой набор осуществляется умножением матриц, в виде произведения матрицы пересчёта и вектора значений. Сами пересчёты можно комбинировать, тоже через умножение матриц. Правила умножения такие: для вычисления числа в некоторой клеточке нужно сложить получающиеся произведения, пробежавшись в одной исходной матрице по той же строке, а в другой матрице по той же колонке. Только, выбор по какой из них в каком направлении бежать влияет на результат, поэтому становится важным, какая матрица слева, а какая справа.

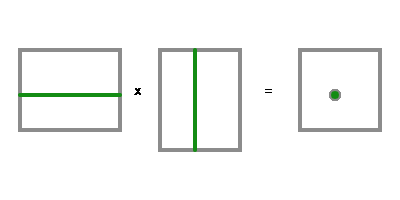
Конечно, некоторые матрицы могут терять значения, почти как при умножении на ноль. Но зато, у тех, которые значения не теряют, есть и обратные матрицы, способные вернуть прежнее значение умножением на результат.

Среди матриц есть аналог обычного числа. Это квадратная матрица, у которой это число расставлено по диагонали. И если такую матрицу умножить на вектор, то будет тот же вектор, умноженный на это число.

У единицы есть свой аналог, $\small\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ , а у мнимой единицы аналогом может быть не только мнимая единица на диагонали. В матрице размером два на два можно поставить единицу и минус единицу по второй диагонали, $\small\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$ , и в квадрате такая матрица будет давать минус один. В каком порядке расставлять на диагонали один и минус один не важно, главное выбрать, какой порядок относится к используемой мнимой единице, а какой к её знаковой противоположности.

Интересно было бы посмотреть, а что возведение в квадрат теряет. Разберём это в общем виде.

Для матрицы $\small\begin{bmatrix} a & b \\ c & d \end{bmatrix}$ результат возведения в квадрат это $\small\begin{bmatrix} aa+bc & ab+bd \\ ca+dc & cb+dd \end{bmatrix}$ .

И если мы хотим этим действием получить обычное число $\small\begin{bmatrix} x & 0 \\ 0 & x \end{bmatrix}$ , то нужно решить систему уравнений

$\begin{cases} aa + bc = cb + dd = x\\ ab + bd = ca + dc = 0 \end{cases}$

В первом равенстве, $a^2 = d^2 = x - bc$ , есть квадраты, а значит, возможно как совпадение так и различие знака.

Во втором равенстве, $b(a+d)=c(a+d) = 0$ , условия верности могут быть на выбор: либо $a + d = 0$ , либо $b = c = 0$ .

Когда верно только $a + d = 0$ , то получается, что величины $a^2$ и $d^2$ могут отличаться от $x$ .

Например, матрица $\small\begin{bmatrix} n & (x-n^2)/m \\ m & -n \end{bmatrix}$ в квадрате даёт $\begin{bmatrix} x & 0 \\ 0 & x \end{bmatrix}$ .

Ого! — теряется уже не знак. Теряются две величины, $n$ и $m\;$ .

И можно отметить, что случаи $n^2 = x$ и $n^2 = 0$ можно разделить, а их смесь точно также будет выполнять равенство.

$\left(\cos(\varphi)\begin{bmatrix} \sqrt{x} & 0 \\ 0 & -\sqrt{x} \end{bmatrix}+\sin(\varphi)\begin{bmatrix} 0 & \sqrt{x}/m \\ \sqrt{x}\,m & 0 \end{bmatrix}\right)^2 =\begin{bmatrix} x & 0 \\ 0 & x \end{bmatrix}$

— При любом $\varphi$ .

Вывернем квадрат наизнанку и посмотрим, что значит корень.

$\left(\begin{bmatrix} \sqrt{x} & 0 \\ 0 & 0 \end{bmatrix}\pm \begin{bmatrix} 0 & 0 \\ 0 & \sqrt{x} \end{bmatrix} \right)^2 =\begin{bmatrix} x & 0 \\ 0 & x \end{bmatrix} =\left( \begin{bmatrix} 0 & 0 \\1 & 0 \end{bmatrix}+ \begin{bmatrix} 0 & x \\ 0 & 0 \end{bmatrix} \right)^2$

Плюс/минус слева говорит, что существует корень из единицы, не равный ни единице, ни минус единице. С учётом знака, их даже два. А с правой частью что?

$\begin{bmatrix} 0 & 0 \\ a & 0 \end{bmatrix}^2=\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}=\begin{bmatrix} 0 & b \\ 0 & 0 \end{bmatrix}^2$

У нас тут нарисовался корень из нуля, сам не равный нулю. А ещё, от такого значения нельзя подсчитать корень. Нет такого значения матрицы, чтобы возвести в квадрат и получить его.

Видимо, чтобы при вычислении корня были получены любые значения, нужно предусмотреть добавление произвольной величины, которая этим способом не достигается. Соответственно, и вычисление квадрата теряет эту информацию. Как будто существования шести различных корней из единицы, без учёта сочетаний ( $\varphi$ ) и дисбалансированных значений ( $m$ ), было для учёта потерь недостаточно.

Расширение матрицы

Данный этап это так называемая «эйфория».

Мы допускаем, что элементы матриц могут быть комплексным. Это расширяет представление и влияет не только на то, что мнимая единица может быть обозначена кроме $\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$ ещё и $\begin{bmatrix} i & 0 \\ 0 & i \end{bmatrix}$ , но и на то что величины $n$ и $m$ — тоже могут быть комплексными.

При $m=i$ получается, что может существовать ещё один корень из единицы, $\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}$ . Более того, этот корень может включиться в пару перетекающих друг в друга корней, и вариантов корней из единицы вместо шести станет восемь: единица, минус единица и сфера значений из трёх составляющих, включающая их знаковые противоположности:

$x^2+y^2+z^2=1 $

$\left(x\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}+ y\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}+ z\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\right)^2= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

$\left(x\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\right)^2+ \left(y\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}\right)^2+ \left(z\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\right)^2= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

Другие составляющие при раскрытии скобок пропадают, потому что являются суммой произведений матриц в двух возможных направлениях:

$\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}= \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$

$\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}= \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$

А для всех трёх пар противоположные порядки произведения приводят к одинаковым результатам с противоположным знаком. То есть, в сумме дают ноль.

Если все элементы матриц поделить на $i$ , то выяснится, что для минус единицы будет такая же сфера значений:

$\begin{bmatrix} i & 0 \\ 0 & i \end{bmatrix}^2 = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} = \left(x\begin{bmatrix} -i & 0 \\ 0 & i \end{bmatrix}\right)^2+ \left(y\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}\right)^2+ \left(z\begin{bmatrix} 0 & -i \\ -i & 0 \end{bmatrix}\right)^2$

Справа посередине как раз матричное представление мнимой единицы через действительные значения элементов. А вместе с остальными двумя матрицами справа и простой единицей образует базу кватернионов. Это — числа подобные комплексным, но в которых используются уже две мнимые единицы, которые при различном порядке произведения образуют плюс или минус третью мнимую единицу, которая от них ничем, кроме порядка в тройке, не отличается.

$i\times j\times k=k\times k=-1 \\ i\times k\times j=-j\times j=1$

$\\A\times B = C\quad C+D=0 \quad B\times A = D \quad A\times B = -D \\-1=A\times B\times C=C\times C=-A\times B\times D=D\times D$

Отсутствие отличия между мнимыми единицами говорит о том что при умножении одинаковых матриц вектор возможных значений схлапывается, теряя направление в базисе, да и сам базис. Соответственно, корень должен возвращать не только длину вектора, но и направление, то есть, привязывать его к базису. Получается, в каком-то смысле, возвращать базис.

Раскрытие комплексного числа через матрицу показывает, что порядок матрицы — количество строк и колонок — удваивается, и для одного шага перевода нужно выбрать, в какой тип представления превратить мнимую составляющую. И есть два отдельных варианта: сохранять комплексное значение на диагональных элементах, или выбрать для мнимой части значение из целой сферы значений. При этом, мнимые составляющие пропадают только у одной пары значений — из всей сферы. То есть, базис разложения в сферу в двух из трёх составляющих сохраняет мнимость элементов, то есть, для следующего уровня разбиения предлагает опять два варианта представления, причём, второй вариант опять сфера. И количество разбиений не ограничено.

Таблица умножения для матриц, строка на колонку:

${\begin{matrix} 1=\begin{bmatrix}1&0\\0&1\end{bmatrix}\\ i=\begin{bmatrix}0&-1\\1&0\end{bmatrix}\\ \end{matrix}} \qquad{\begin{matrix}1 & i & L & H\\i & -1 & H & -L \\H & L & i & 1 \\L & -H & 1 & -i\end{matrix}}\qquad {\begin{matrix} H=\begin{bmatrix}0&1\\1&0\end{bmatrix}\\ L=\begin{bmatrix}1&0\\0&-1\end{bmatrix}\\ \end{matrix}}$

Если у двух из трёх мнимых единиц кватерниона поменять знак, закономерности от этого не изменятся. Но в расширенном виде можно сохранить закономерности, проведя частичное изменение знака у всех трёх единиц сразу:

$\quad i:\begin{bmatrix}0&-1\\1&0\end{bmatrix} =\begin{bmatrix}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{bmatrix} \rightarrow \begin{bmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{bmatrix} =\begin{bmatrix}0&-L\\L&0\end{bmatrix}:j\quad$

$\quad j:\begin{bmatrix}0&i\\i&0\end{bmatrix} =\begin{bmatrix}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{bmatrix} \rightarrow \begin{bmatrix}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{bmatrix} =\begin{bmatrix}0&-H\\H&0\end{bmatrix}:k$

$\quad k:\begin{bmatrix}-i&0\\0&i\end{bmatrix} =\begin{bmatrix}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix} \rightarrow \begin{bmatrix}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix} =\begin{bmatrix}i&0\\0&i\end{bmatrix}:i\qquad$

Вот это поворот.

Оказывается, матричное представление с мнимой единицей на диагонали — тоже часть сферы. У него тоже есть значения матриц, которые соответствуют другим мнимым единицам кватерниона. Да, наверное, и всей мнимой гиперсферы, если расширять матрицу сразу с мнимой единицей на диагонали.

Произведение двух величин из различных мнимых гиперсфер будет давать значение из гиперсферы матриц паули — уже упомянутых корней из единицы, не совпадающих с самой единицей. Две мнимые гиперсферы образовались от выбора представления мнимой единицы не совпадающей с i на диагонали — на всех шагах расширения, и отражения этого решения на базис, включающий исключительно диагональное расположение. Но различное представление можно выбирать на каждом шаге расширения и даже отдельно для каждого мнимого элемента. Разнообразие результатов у произведения значений при этом заметно вырастает. Дополнительно можно рассмотреть и использование расширения единиц на матрицы паули. Ещё можно рассмотреть использование других простых чисел для коэффициента расширения матриц. Количество возможных значений тогда сильно растёт.

Но до октонионов — значений с третьей базовой мнимой единицей $l$ — таким образом не добраться: если расставить скобки в цепочке произведения октонионов с последнего элемента как самого глубоко вложенного, то результат может отличаться. $i(jl)=-kl\ne kl=(ij)l$ . Из-за этой неассоциативности октонионы не имеют матричного представления, ведь умножение матриц ассоциативно.

«Лучше всего, конечно, пять звёздочек»

Ну, а самое лучше это использовать морфина гидрохлорид, пятипроцентный раствор.

Для матриц второго порядка даже при использовании только действительных значений элементов к комплексному числу $\small\begin{bmatrix} a & -b \\ b & a \end{bmatrix}$ могут быть добавлены «делители нуля» $\small\begin{bmatrix} 0 & x \\ 0 & 0 \end{bmatrix}$ , $\small\begin{bmatrix} 0 & 0 \\ x & 0 \end{bmatrix}$ и «получисла» $\small\begin{bmatrix} 0 & 0 \\ 0 & x \end{bmatrix}$ , $\small\begin{bmatrix} x & 0 \\ 0 & 0 \end{bmatrix}$ , что говорит, что значения матриц не ограничиваются гиперсферическими числами. Произвольные величины не ограничиваются матрицами.

Матрицы представляют собой схемы пересчёта одних векторов в другие, а добавочные значения (делители нуля и получисла) имеют признаки схлапывания — применённые в чистом виде они забирают возможность точного восстановления. Соответственно, для того чтобы обратить этот процесс, стоило бы придумать такие структуры, которые сохраняют значение, и при обратной операции его восстанавливают.

Как восстанавливаются значения, если они не потеряны? У матрицы второго порядка есть такая закономерность:

$\begin{bmatrix} a & b \\ c & -d \end{bmatrix}\begin{bmatrix} d & b \\ c & -a \end{bmatrix} =\begin{bmatrix} ad+bc & ab-ba \\ cd-dc & cb+da \end{bmatrix}$

Если одну из матриц поделить на $ad+bc$ , то справа будет единичная матрица и матрицы станут обратными друг другу — одна будет обращать действие другой.

Величина $ad+bc$ — это взятый с минусом определитель матриц из левой части равенства. Определитель может быть вычислен для квадратных матриц любого порядка. Это как обобщённый объём обобщённого параллелепипеда из составляющих матрицу векторов. Если определитель матрицы равен нулю, значит матрица схлопнула пространство преобразуемых векторов — хотя бы по одной координате, и тогда единственное скалярное значение, которое две матрицы могут дать при умножении — это ноль.

Одна перестановка столбцов или строк матрицы переключает знак у определителя — точно так же как знак результата меняется от изменения порядка произведения мнимых единиц.

Такими перестановками можно расставить по диагонали бóльшие элементы, оставив меньшие элементы вне диагонали — сравнение останется в рамках строки и колонки. И тогда матрицу как действие можно поделить — на скомпенсированную этими перемещениями часть, которая говорит о перестановке элементов вектора, и на остальное влияние значений друг на друга, которое является уже не обобщённым разворотом в пространстве, а некоторым обобщённым искажением.

Расчёт определителя основан на том, что если в матрице на всю колонку будет только одна единица, то результат будет равен, с точностью до знака, определителю матрицы без этой строчки и колонки. И если единицу «размазать» по колонке, то части определителя складываются линейно. Для объяснения вычисления вполне достаточно.

Для матрицы порядка два определитель это разница произведений элементов обеих диагоналей. Если элемент матрицы кватернион, то определитель считается всё же по действительному представлению матрицы, но и тут при ненулевом определителе возможно найти обратную матрицу.

Это будет задача со звёздочкой.

$\begin{bmatrix} a & b \\ c & -d \end{bmatrix}\begin{bmatrix} d^* & b^* \\ c^* & -a^* \end{bmatrix} =\begin{bmatrix} ad^*+bc^* & ab^*-ba^* \\ cd^*-dc^* & cb^*+da^* \end{bmatrix}$

Если выписать требования явно, то получится следующее:

$a b^*-b a^*= c d^*-d c^*=0 \\a d^*+b c^*=d a^*+c b^* =1$

Две операции, перестановка множителей и модификация второго множителя, проводимые одновременно, должны компенсировать друг друга. Для двух пар множителей компенсировать полностью, а для других двух пар — в сумме. То есть, для них различия должны быть одинаковыми, с противоположным знаком.

$da^*+bc^*+\Delta=1$

$\begin{matrix} a&\leftrightarrow &b\\ +\Delta\downarrow\qquad&&\qquad\downarrow-\Delta\\ d&\leftrightarrow &c\\ \end{matrix}$

$ad^*-da^*=\Delta=cb^*-bc^*$

Оставшиеся две пары пар как будто даже и не связаны. Хорошо, что решение только одно, правда?

Полезно вспомнить, что изменение порядка в произведении обратных друг другу матриц не меняет результат. И что значения $qqpp$ и $ppqq$ разделяет четыре перестановки соседних множителей.

Основание

Дело в том, что — видите.

В нулевой степени любая величина станет единицей, а в единичной степени будет собой. Промежуточные степени возможны, но на комплексной плоскости они расположены на спирали, именно поэтому промежуточная степень $1/2$ может завернуть на значение $(-\sqrt{x})$ . Сколько витков проходит пока степень меняется на единицу — неизвестно. Для положительных чисел в основании есть особый вариант — ноль витков, но для отрицательных такого варианта нет — для определённости количество поворотов за один шаг нужно выбрать между положительными и отрицательными полуцелыми числами.

Для показательной функции $n^x$ производная будет той же самой функцией, умноженной на коэффициент. То есть, каким бы значением показательной функции не было, небольшое изменение аргумента приведёт к изменению, которое приблизительно равно произведению этого изменения, самой функции, и константы, которая зависит только от основания.

$(n^x)'_x=n^x \ln(n)$

Эта функция от основания — натуральный логарифм. Это обычный логарифм как функция определения показателя степени по выбору основания и результату, но основание у него — это некоторое число $e$ . Оно подобрано так, что если основание с ним совпадает, то константа как множитель становится не нужна, она становится единицей. При этом производная функции совпадает с самой функцией, в этом и есть особенность числа $e$ .

$(e^{x})'_x=e^{x}$

Если основание оставить, но в степени перед аргументом поставить постоянный коэффициент, то производная увеличится во столько же раз.

$(e^{kx})'_x=ke^{kx}$

Если коэффициент мнимая единица, то изменение функции становится вращением на комплексной плоскости и через изменение аргумента равное длине единичной окружности функция повторяет своё значение.

$e^{\frac{\pi}{2}i}=i$

Всё это приводит к одному выводу: результат вычисления логарифма определён по мнимой составляющей с точностью до оборота. То есть, логарифм как вычисление принципиально не может сообщить о номере витка, только о сдвиге в его рамках.

$e^{a+bi+2\pi n i}=x\quad \Rightarrow \quad\ln(x)=a+bi+2\pi k i\qquad a,b\in\mathbb{R}\quad n,k \in \mathbb{N}$

Наглядно видно процесс потери и восстановления. Восстановления не всегда того что потеряно.

Особенности логарифма

То оно, например, видно сразу, чем отличается от чего.

Производная от степенной функции будет произведением показателя и переменной в степени на единицу меньшей. Если подсчитать первообразную обратно, то получится, что нужно делить на величину $n+1$ . Если $n$ приближается к $(-1)$ , то первообразная приближается к натуральному логарифму.

$(x^n)'_x=nx^{n-1}\quad x^{n}=\left(\frac{x^{n+1}}{n+1}\right)'_x\quad \int\limits_1^y\frac{dx}{x^s}=\frac{y^{1-s}-1}{1-s} \quad \int\limits_1^y\frac{dx}{x}=\ln(y)$

В интеграле если верхний предел $y$ не положительное значение, то значение интеграла зависит от пути интегрирования. Оно зависит от пути и при положительном значении, но среди вариантов есть один особенный, самый простой. Ещё, путь должен быть расположен в одной комплексной плоскости — используя только одну выделенную мнимую координату, иначе появляется разница в том с какой стороны умножать на дифференциал, и одним вариантом, или их усреднением, не обойтись.

Производная логарифма игнорирует любой постоянный коэффициент у аргумента:

$(\ln(k \cdot x))'_x=\frac{1}{x}\qquad kx\ne 0$

При разборах показательной и степенной функций переменная была то в показателе, то в основании, но всё равно натуральный логарифм проявился. Можно попробовать разобраться почему. Заменим $1-s$ на $s$ :

$\int\limits_1^e \frac{x^{s}}{x\,\,}{dx}=\frac{e^{s}-1}{s} \qquad e^s=1+s\int\limits_1^e \frac{x^{s}}{x\,\,}\,{dx}$

После замены переменных:

$\int\limits_0^1 {y^{sx}}\,{dx}=\frac{y^{s}-1}{s\ln(y)} \qquad e^s=1+s\int\limits_0^1 e^{sx}\,{dx}\cdot \ln(e)$

Можно $e$ и $s$ поменять местами, только натуральный логарифм не исчезнет.

$s^e=1+e\int\limits_0^1 s^{ex}\,{dx}\cdot \ln(s)$

Здесь $e$ может быть любым, можно приравнять $s$ , или единице:

$s^s=1+s\int\limits_0^1 s^{sx}\,{dx}\cdot \ln(s) \qquad s=1+\ln(s)\int\limits_0^1 s^{x}\,{dx}$

Отсюда можно вывести ещё одно выражение для логарифма:

$\frac{s-1}{\ln(s)}=\int\limits_0^1 s^{x}\,{dx} \qquad \ln(s)=\frac{s-1}{\int\limits_0^1 s^{x}\,{dx}} \qquad \ln(s) =\frac{s^k}{\int\limits_{\pm\infty}^{k} s^{x}\,{dx}}$

Интересная неопределённость нижнего предела, знак зависит от самого $s$ .

Циклическая неопределённость мнимой части логарифма остаётся, так как интеграл перед тем как из начальной точки дойти до конечной может покружить любое количество раз в любую сторону вокруг ноля, особенно если $s$ отрицательное. Конечно, всё в рамках одной комплексной плоскости. Для удобства можно условиться — расставить для какого аргумента какой вариант логарифма будет считаться основным.

${a^b} = 1+\int\limits_{0}^{b}\int\limits_1^a \frac{a^y}{x}\,dx\,{dy}$

Такая формула для степени получается при совмещении двух формул для логарифма.

Две параметризации

[Что одно — что другое, разница не имеет принципиального значения] — это можете вырезать полностью.

Рассмотрим различие порядков операции на примере произведения кватернионов. Вот как выглядит произведение двух кватернионов в таком базисе, в котором у обоих нет третьей составляющей векторной части:

${(r+xi+yj)\times (r^*+x^*i+y^*j)= \\\qquad= (rr^*-xx^*-yy^*)+ \\\qquad +\,(rx^*+r^*x)\,i+ \\\qquad +\,(ry^*+r^*y)\,j+ \\\qquad +\,(xy^*-x^*y)\,k}$

У результата появляется третья составляющая, а её знак зависит от порядка произведения.

Произведению можно добавить такой параметр, который будет характеризовать порядок: при параметре 1 порядок совпадает с исходным, при параметре (-1) порядок обратный, при нулевом параметре различие уменьшается до нуля. Это можно сделать через коэффициент у перпендикулярной к общей плоскости обоих векторов составляющей.

В таком параметре есть два направления, плюс и минус. Всего два? По теореме Эскобара стоит добавить ещё направлений. Новое направление это будет средним между известными двумя: направлением первого вектора и направлением обращённого по знаку второго вектора. Тогда векторную часть результата произведения можно будет перенаправить двойным параметром по любому направлению на плоскости, на выбор. Обращение одного из векторов перед расчётом дополнительного направления здесь понадобилось для того чтобы при обмене векторов менялся и знак результата.

Параметр можно дополнить и третьим базисным направлением, рассчитанным просто как среднее между направлениями исходных векторов — оно будет перпендикулярно первым двум базисным направлениям. Но плавный обмен направлений исходных векторов не поменяет знак такого среднего направления. Поэтому результат определён только с точностью до знака, у одной составляющей выделенного базиса знак будет неопределён. Такие неопределённые значения — это уже не кватернионы, даже парой кватернионов они будут только до следующего произведения с такой же математической структурой с другим направлением неопределённости.

Различие порядка операции возведения в степень похоже на различие порядка при умножении кватернионов. «Гипотезой Эскобара» — я называю предположение о том, что возведение в степень можно параметризовать, примерно так же как выше умножение кватернионов.

У возведения в степень при одинаковом основании и показателе $x^x$ должна существовать обратная операция, подобно корню — обратной к операции умножения величины на саму себя. $x=\pm\sqrt{x\times x}$ . Эту функцию можно обозначить напрямую, $x=Q_n(x^\wedge x)$ , а можно выразить через функцию Ламберта.

$y=\ln(x)\qquad x=e^y\qquad {W}(xe^x)=x \\s=x^x=e^\wedge{(\ln(x)\cdot x)}=e^\wedge{(ye^y)} \qquad\ln(x^x)=ye^y \\{W_n}(\ln(x^x))={W_n}(ye^y)=y=\ln(x)$

Получается

${x=e^{{W_n}(\ln(s))}}$

Так что, если взять экспоненту $e^x$ , умножить на аргумент, $xe^x$ , обратить функцию, обменяв значение и аргумент, $W_n(x)$ , затем произвести у графика логарифмическую замену обеих координат $e^{W_n(\ln x)}$ , то останется одно обращение функции, чтобы получить $x^x$ .

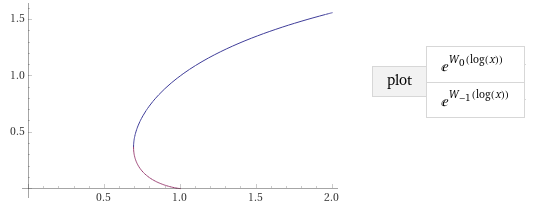
Интересно, как работают такие фокусы при использовании комплексных значений?

Если эту морковку развернуть, то ботва совпадёт с предыдущим графиком.

Если основание и показатель различаются, то зная их соотношение всё равно можно восстановить значения по результату, практически тем же самым способом.

$s=(ax)^{x}\qquad x=e^{W_n(\ln(s)\cdot a)}/a\qquad a\in(0;1]$

Чтобы представлять как устроено возведение в степень можно попробовать вращать значение $x$ в комплексной плоскости. Если начать с единицы, то $x^x$ будет единицей, затем изменение аргумента опишут следующее изменение результата:

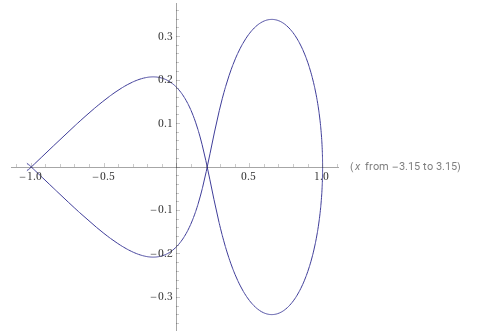
Видно, что в точке $x=i$ значение выражения $x^x=i^i=e^{\frac{\pi}{2}i\cdot i}$ становится действительным, $e^{-\pi/2}=0,2078\ldots$

В точке (-1) сам аргумент $x$ заворачивает на новый круг, как при движении по часовой, так и против часовой. Но у $x^x$ при движении по