GFDM и тензоры. Продолжение
Сначала я хотел не углубляться в тензоры и описать их мимоходом, касаясь только используемого мной функционала. Однако я изменил свое мнение и решил рассказать больше. Добро пожаловать в многомерный мир.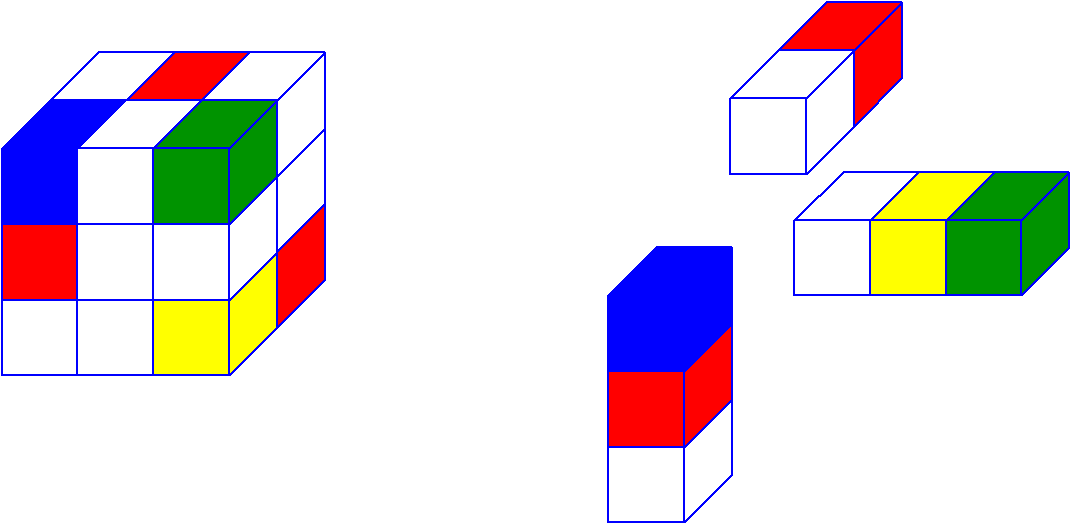
CP — CANDECOMP/PARAFAC
CANDECOMP — Canonical decomposition
PARAFAC — parallel Factors
PARATCUK2 — PARAFAC/Tucker2
ALS — Alternating least squares
ПМНК — перемежающийся метод наименьших квадратов
SVD — Singular value decomposition
СЛАУ — Система линейных алгебраических уравнений
GFDM — generalized frequency division multiplexing
SECSI — SEmi-algebraic framework for approximat eCP decompositions via SImultaneous Matrix Diagonalizations
Используемые обозначения
Тензоры
Пожалуй наилучшим определением тензора будет цитата Tamara G. Kolda:
A tensor is a multidimensional array
Проще некуда. Идеи с тензорами возникли изначально в линейной алгебре. Поэтому лучший путь — описать все используя линейную алгебру. В линейной алгебре мы пользуемся скалярами, векторами, матрицами и можем совершать операции сложения, вычитания и умножения. Скаляр состоит из 1 элемента, вектор состоит из N элементов и матрица состоит из MN элементов. Тензоры включают в себя все что может линейная алгебра и даже немного больше. Приводя примеры из линейной алгебры: вектор — это тензор первого порядка, а матрица — это тензор второго порядка. Следовательно порядок тензора определяется количеством пространств в которых тензор имеет больше чем один элемент. Чем больше у Вас пространств, тем выше получается порядок тензора. Достаточно просто, верно?
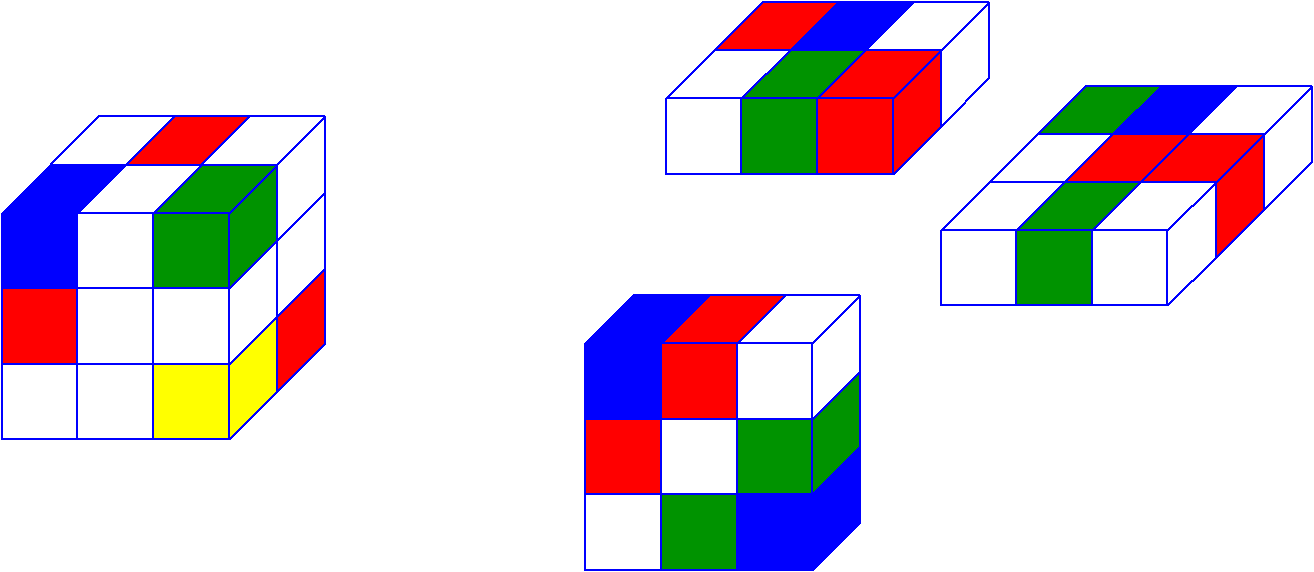
Давайте сразу приведем пример тензора третьего порядка. Знакомьтесь, с этим тензором Вы сегодня будете работать и на нем увидите немного тензорной магии. Я выписал его фронтальные срезы ниже.
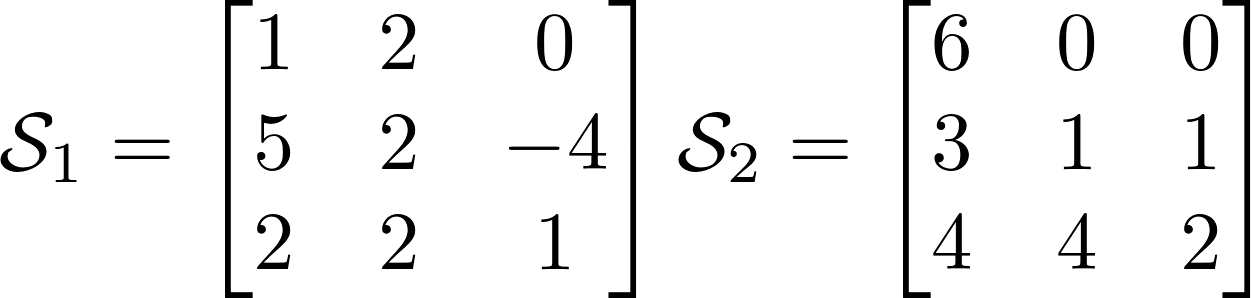
Линейная алгебра определяет нам произведение между двумя матрицами следующим образом:
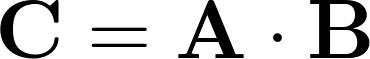
В этом произведении задано две размерности и операция между объектами с размерностью больше двух не определена. Тензорная алгебра дает инструменты как обойти это ограничение, используя особенности большего количества пространств в линейной алгебре. Для начала я введу три матричные операции, без которых в тензорной алгебре и шагу не ступишь:
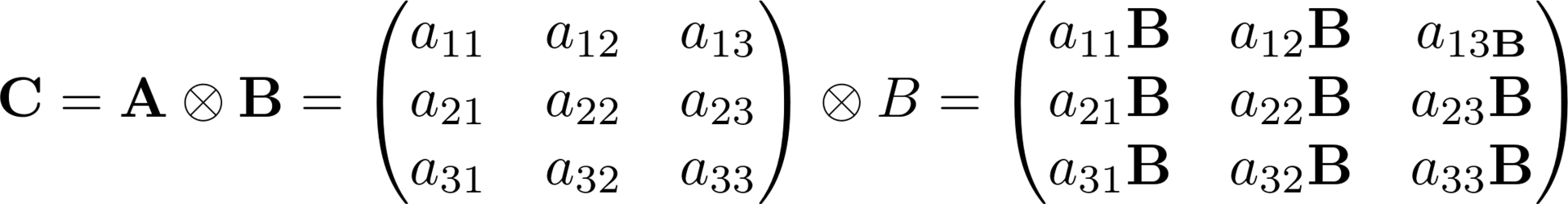
Эта операця используется для формирования упрощенной модели канала в МИМО.
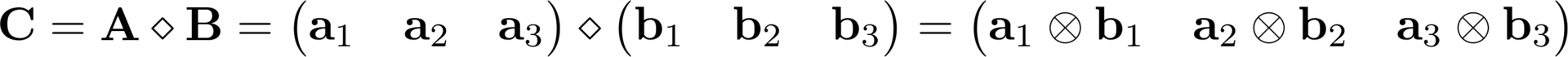
Эта операция чаще всего используется в тензорах третьего порядка, к примеру именно через нее я описал матрицу модуляции системы GFDM
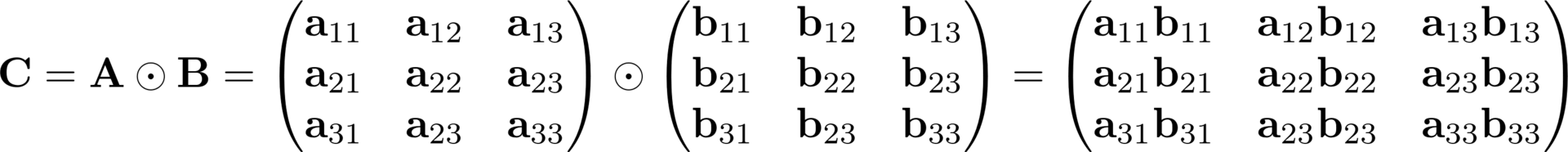
Основные операции в тензорной алгебре
Развертка
В тензорной алгебре одно из ключевых понятий — «unfolding» (Я буду называть его развертка для уменьшения англицизмов) или представление тензора через матрицу. Развертка это отображение тензора на одно из его пространств. Тензор при этой операции записывается как матрица, количество строк которой равно количеству элементов развертываемого пространства. Элементы в строке имеют тот же порядковый номер по заданному пространству.
Существует два вида записи элементов в строку: по нотации Латауэра и по нотации Матлаб. Чаще всего используется нотация Матлаб, поэтому я буду использовать ее. По нотации Матлаб, элементы идут по возрастанию в размерности, т.е. сперва идет элемент по первой размерности, затем по второй и так далее исключая развертываемую размерность.
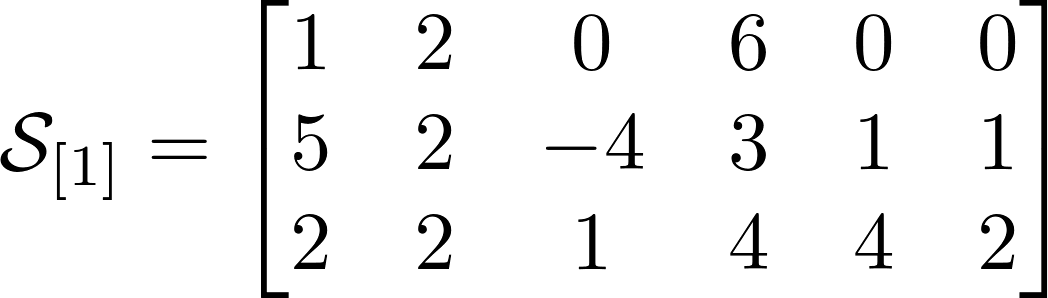
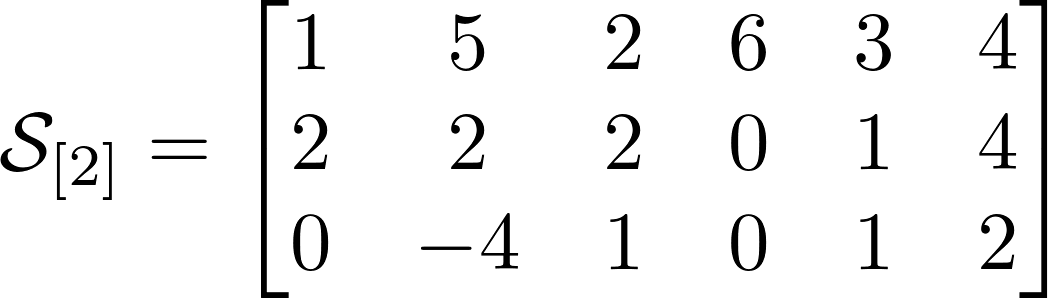
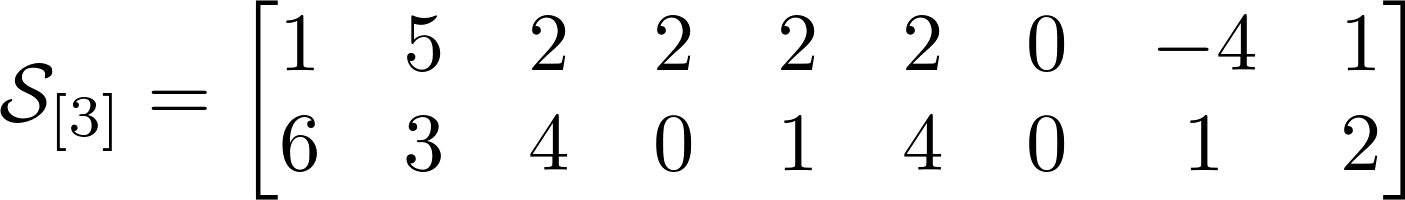
Количество возможных разверток равно порядку тензора или его размерности. У тензора из нашего примера есть 3 развертки. Выше представлены развертки для нашего тензора, и я надеюсь по ним Вам будет значительно проще понять, чем по объяснениям. Тензоры показались мне гораздо понятнее в интуитивном смысле, нежели чем по определениям.
Произведение по заданному пространству
Следующая операция которую я хочу описать, это произведение тензора с матрицей по заданному пространству. Записывается оно следующим образом и в сущности это произведение двух матриц, где правая матрица — это развертка тензора по умножаемому пространству, а слева матрица с которой собственно и умножают.
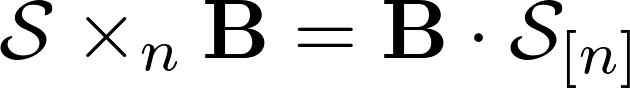
Важный момент, умножение записывается справа, а происходит слева от тензора. В результате получается матрица являющаяся разверткой нового тензора, который можно собрать обратно в привычный тензор. Важно отметить, что в результате этой операции размерность пространства с которым происходит умножение может измениться, остальные не могут. Пример ниже
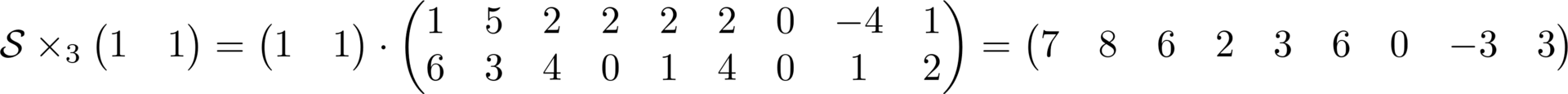
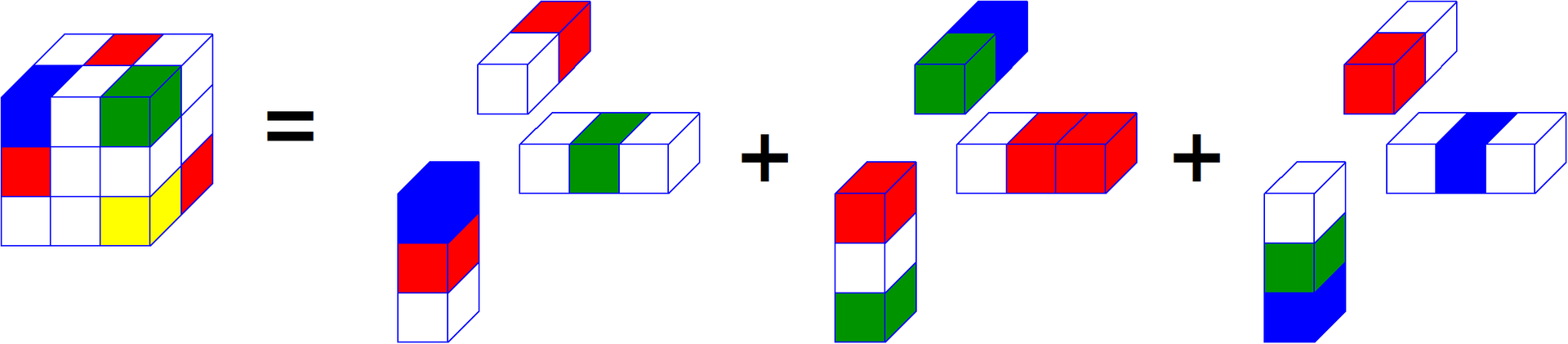
Тензор единичного ранга
Тензор единичного ранга — это такой тензор размерности N, который можно получить если умножить единицу на N векторов, по одному на каждое пространство. Как это выглядит визуально для тензора третьего порядка я показал ниже. Тензор единичного ранга является аналогом одной компоненты для SVD матрицы, где сложная матрица раскладывается на матрицы единичного ранга. Тензор единичного ранга может быть как комплексным так и вещественным, в зависимости от требований которые мы к нему предъявляем.
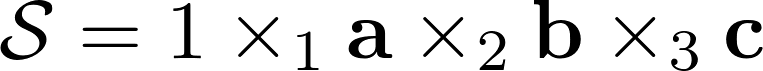

Разложение тензоров
Самое важное и интересное в тензорах это их разложения. Я надеюсь многие из Вас знают или слышали о разложении матрицы на сингулярные значения. При помощи него мы можем представить матрицу как сумму матриц единичного ранга, и оценить их вклад в общую матрицу. Чуть ниже представлен пример такого разложения.
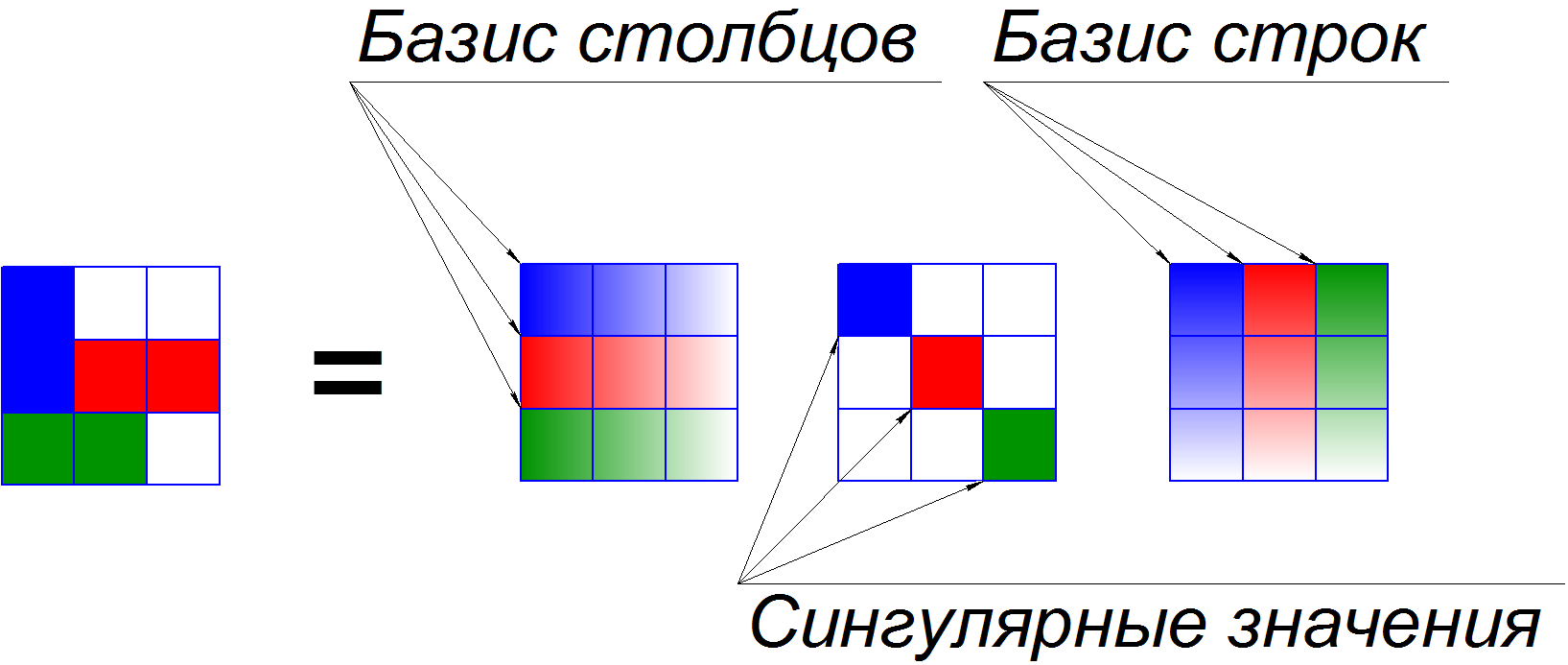
Очень похожий аналог есть в тензорной алгебре и называется он «CP», его называют еще «CANDECOMP» или «PARAFAC». «CP» раскладывает любой тензор на сумму тензоров единичного ранга. У этой формулировки есть две формы записи, простая из которых действительно записывает тензор как сумму множества тензоров единичного ранга, другая же записывает разложение через матрицы по каждому из пространств. Кроме разложения «CP» в тензорной алгебре существует большое количество его аналогов, в зависимости от нормирования компонент и прочих особенностей.
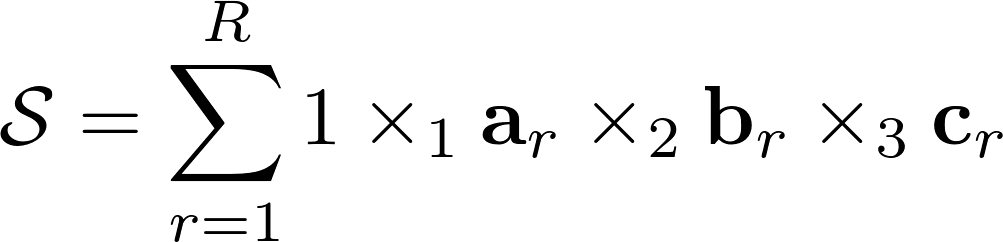
Посмотрите, если записать вектора каждого из пространств одно за другим, будет получено N матриц. Каждая из матриц представляет некий «базис» по своему пространству. Такая форма записи напоминает SVD матрицы. Из этих матриц можно получить обратно тензор, если взять единичный тензор и попеременно умножить его на все матрицы-базисы по пространствам.
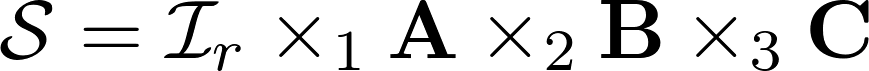
Из разложения тензора третьего порядка легко вывести выражение развертки, оно позволит отделить одну из матриц обычным матричным произведением. Посмотрите ниже, видите, матрица А записывается через произведение с другой матрицей, которая в свою очередь является продуктом произведения Хатри-Рао. Зная продукт произведения и исходную развертку, мы можем вычислить матрицу А используя линейную алгебру. Это значительно упрощает работу алгоритмов подсчета разложения для тензоров третьего порядка и дает удобные формулы для итераций.
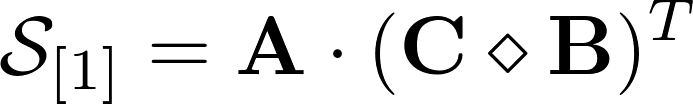
Зачем вообще нужна эта ерунда, мы же могли сделать SVD развертки? Конечно могли, но в общем случае разложение тензора позволяет гораздо проще описать данные, их становится проще сжать или найти закономерности. Особенно это важно для больших объемов данных, так как с увеличением размерностей ранг изменяется значительно слабее.
Проблемы разложения
У этого разложения при всей его прелести есть две проблемы. Первая: ранг этого разложения нужно узнать Вам самим. Зачастую это нетривиальная задача, особенно если данные имеют шум.
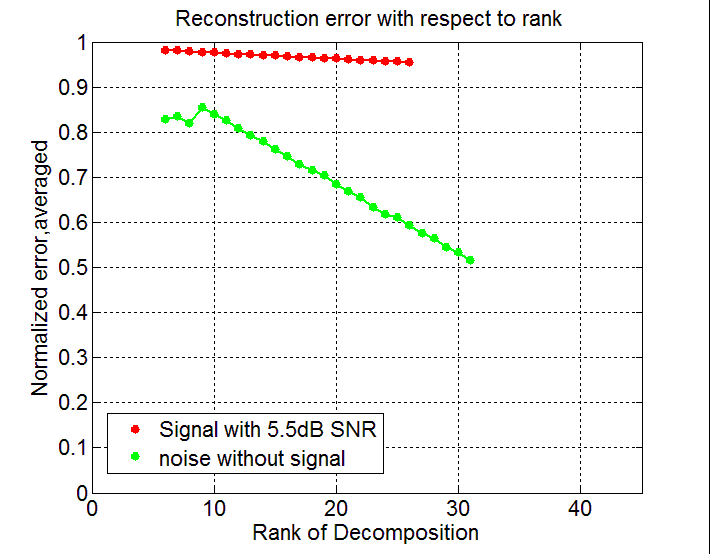
Алгоритм был по поиску GPS сигнала при вычислении корреляции полифазным преобразованием Фурье. При этом размерность выходных данных на корреляторе была равна четырем (время, частота, код, сдвиг полифазного преобразования).
Вторая проблема — вычисление самого разложения. Самый распространенный на данный момент алгоритм это ALS или ПМНК. Существует так же алгоритм с романтичным названием SECSI, но про него я возможно расскажу в будущем. ПМНК или перемежающийся метод наименьших квадратов прост до безобразия, алгоритм у него следующий:
- Задаем ранг разложения
- Генерируем случайные матрицы разложения пространств
- Фиксируем все матрицы кроме одной и вычисляем оставшуюся матрицу при помощи СЛАУ
- Повторяем по очереди предыдущий пункт для всех матриц, пока невязка не станет приемлемой
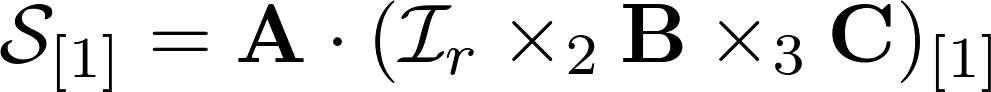
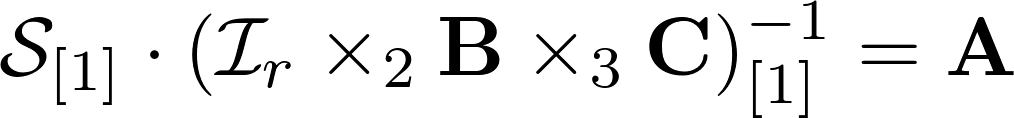
Недостатков у этого метода огромное множество, это и локальные минимумы, и вычислительная сложность, но он все равно остается одним из наиболее используемых алгоритмов в настоящее время.
Связь с GFDM
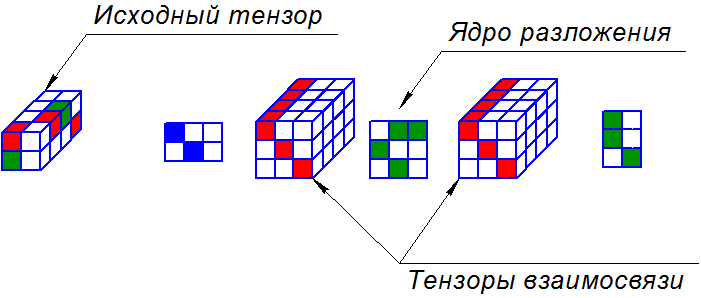
А теперь перейдем ближе к технологии GFDM. Существует другое разложение, которое называется PARATUCK2, и это аббревиатура от двух других аббревиатур «PARAFAC» и «TUCKER2». Да, аббревиатура состоящая из двух других аббревиатур, как же это замечательно.
Это разложение записывает тензор через три матрицы и два тензора. Матрица посередине называется ядром разложения, тензоры называются объединяющими. Крайние две матрицы не имеют особого названия. То как считать тензор из этого разложения это отдельная история.

Тензор из разложения считается послойно, в каждом слою выбирается только соответствующий слой тензоров взаимосвязи. В результате получаются 5 матриц, перемножив которые мы и получаем значения тензора. Эта операция повторяется по каждому из слоев, и результаты собираются один за другим. Количество строк первой матрицы равно количеству строк у тензора, аналогично со столбцами третьей матрицы и тензора, а так же с глубиной тензоров взаимосвязи. Мне было это очень сложно понять в первый момент. И что самое интересное, эта модель действительно может Вам помочь при анализе данных.
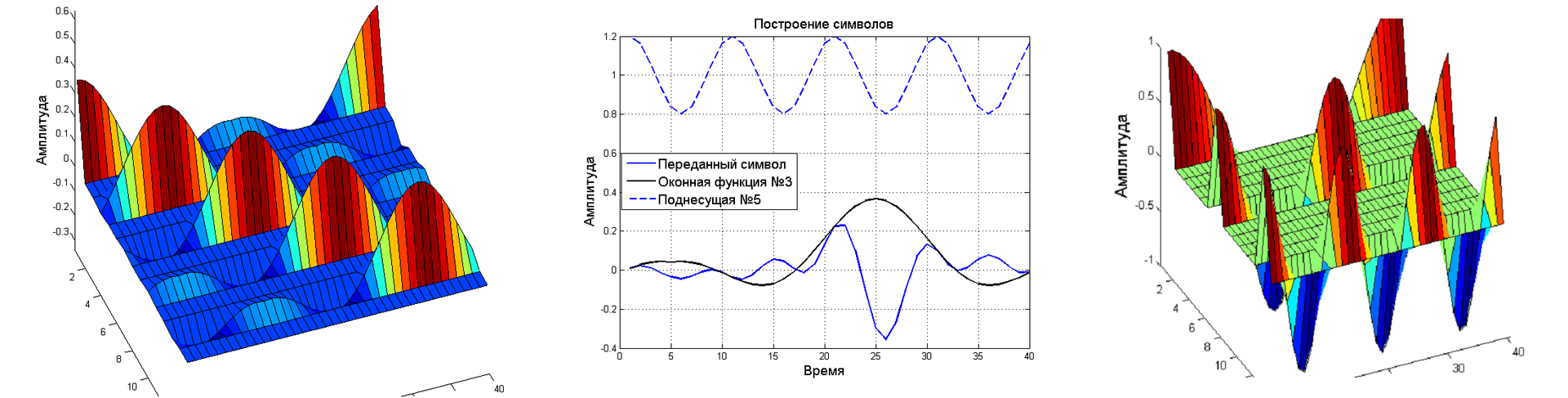
Так зачем нам нужно это разложение? Оно достаточно сложное и состоит из пяти элементов, как оно вообще может помочь с GFDM? Давайте сначала вспомним и закрепим немного о GFDM. Ниже представлен метод формирования символов, который отправляет передатчик. Блок данных можно сформировать как матрицу, где строки это поднесущие, а столбцы это временные позиции в блоке. Общий блок данных получается суммированием всех элементов, иначе говоря надо умножить поэлементно вектор поднесущей с вектором оконной функции и все это на символ который мы передаем. Таким образом каждый символ находится на пересечении двух векторов с которыми и перемножается. Операция достаточно простая, однако ее сложно описать через произведение матрицы модуляции на вектор символов. Форма записи же через матрицу модуляции является основным кирпичиком для построения приемников.
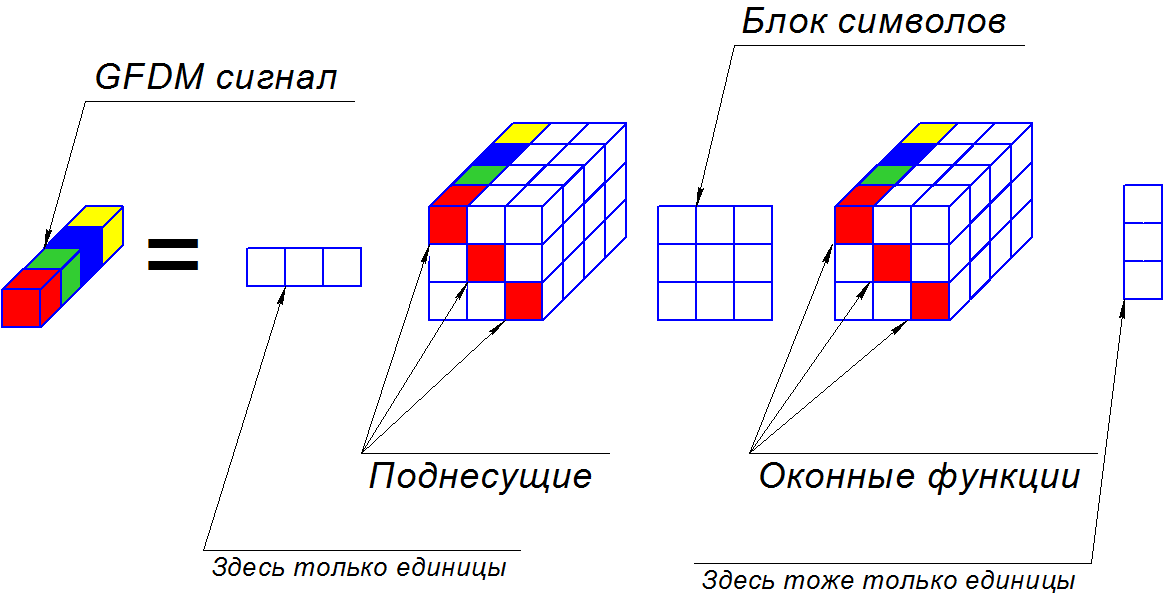
Если присмотреться повнимательнее, PARATUCK2 действительно может описать GFDM. Для этого необходимо взять в качестве крайних матриц единичные вектор строку и вектор столбец, а в тензоры взаимосвязи по главном диагоналям добавить оконные функции и поднесущие. Если в матрице-ядре окажутся символы, результат будет вектором в третьем измерении и соответствовать переданным данным.
Изначально я дополнительно предполагал описать частотозависимый канал канал через значения в векторе рядом с тензором поднесущих. Это было ошибочное предположение
Лихо завернуто, неправда ли? Когда я писал диплом, было сложно понять, как это можно упростить и привести к приемлемому виду, но это возможно! Через это разложение можно упростить выражение модуляционной матрицы в произведение двух матриц. Однако я думаю рассказать в следующий раз, вместе с теорией Zero-forcing, Matched filter и Minimal mean squared error приемников.
T.G. Kolda and B.W. Bader, \Tensor decompositions and applications,» SIAM Review,
vol. 51, no. 3, pp. 455{500, 2009.
R. Bro, N. Sidiropoulos, and G. Giannakis, \Parafac: Tutorial and applications,»
Chemometrics Group, Food Technology, Royal Veterinary Agricultural University, 1997.
L. de Lathauwer, B. de Moor, and J. Vanderwalle, \A multilinear singular value decom-
position,» SIAM J. MATRIX ANAL. APPL. Vol. 21, No. 4, pp. 1253 1278, 2000.
K.B. Petersen and M.S. Pedersen, The Matrix Cookbook. Petersen & Pedersen, 2012.
S. LIU and G. TRENKLER, \Hadamard, khatri-rao, kronecker and other matrix
products,» INTERNATIONAL JOURNAL OF INFORMATION AND SYSTEMS SCI-
ENCES, 2006.
A.L. F. de Almeida, G. Favier, and L.R. Ximenes, \Space-time-frequency (stf) mimo
communication systems with blind receiver based on a generalized paratuck2 model,»
IEEE Transaction in signal processing, vol. 61, no. 8,, APR, 2013.
Хорошей Вам недели.
