Геометрия данных 5. Преобразование базиса27.10.2017 13:18

Под преобразованием базиса системы координат понимается замена одного набора базовых вершин (реперов) на другой. По сравнению с обычной системой координат на векторах изменение системы координат на точечном базисе имеет особенности, связанные с тем, что базисы могут принадлежать разным пространствам.

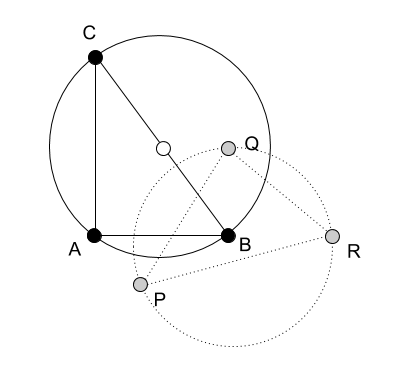
В предыдущей части было рассмотрено определение базиса низкой размерности в пространстве высокой размерности и показано, каким образом можно определять дистанции между вершинами, не принадлежащими пространству базиса. При замене базиса требование сохранения метрических свойств системы координат также является ключевым.

Основные матрицы

Под матрицами преобразования (матрицами перехода) обычно понимают такие матрицы, при умножении на которые координат точки (вершины) в старом базисе, получаются ее координаты в новом. На основании данных матриц преобразуются также метрические тензоры из одного базиса в другой.

Матрицы преобразования базисов содержат сравнительные характеристики двух базисов. Среди данных матриц выделятся инвариантные матрицы — их значения не зависят от выбора базиса. Например, матрица дистанций между вершинами является инвариантной.

Прямые матрицы перехода

Набор исходных базовых вершин обозначим как $a$ (старый базис), новый набор как $p$ (новый базис). Для преобразования координат должна быть задана матрица перехода — описание координат вершин нового базиса в старом. Такими координатами могут быть как ди-координаты вершин, так и би-координаты. Матрицу перехода в ди-координатах обозначим как $Di_{pa}$ . Строка матрицы — это координаты вершины нового базиса $p$ относительно старого $a$ , соответственно столбец — это ди-координаты вершины старого базиса относительно нового.

Матрица перехода должна быть квадратной, следовательно одних координат вершин недостаточно — их количество меньше, чем количество компонент координат (из-за наличия скалярной компоненты в координатах). Поэтому необходимо добавить в данную матрицу координаты ди-вектора [0; 1, 1, … 1]. После чего матрица перехода в ди-координатах становится похожей по форме на дистанционный метрический тензор (ДМТ) (только диагональ ненулевая). Назовем матрицу $Di_{pa}$ дистанционным тензором преобразования координат (ДТП). Ее структура:

$Di_{pa}=\begin{pmatrix} 0 & 1_a \\ 1_p & D2_{pa} \end{pmatrix} \quad(5.1.1)$

Дистанционный тензор преобразования является инвариантом — его значения не зависят от базиса. При обратном переходе (от $p$ к $a$ ) значения даной матрицы просто транспонируются (строки и столбцы меняются местами).

Поскольку ДТП — это ди-координаты, то умножая их на лапласовский метрический тензор (ЛМТ), можно получить би-координаты $Bi_{p}^{ a}$ . Структура би-координат матрицы перехода:

$Bi_{p}^{ a}=\begin{pmatrix} 1 & 0_a \\ m2_p & B_{p}^{ a} \end{pmatrix} \quad(5.1.2)$

Первая строка данной матрицы — это вектор $[1; 0, 0,...]$ , соответствующий скалярной компоненте.
В отличие от ДТП значения би-координат матрицы перехода зависят от того, для какого базиса они получены — для старого или нового. Выбор базиса определяет матрицу ЛМТ. Для определенности би-координаты перехода в базисе $a$ обозначим как $Bia_{p}^{ a}$ , а в базисе $p$ — $Bip_{p}^{\space a}$ . Тогда имеют место следующие тождества для исходного базиса:

$Bia_{p}^{ a}=Di_{pa} Lm^{aa}$ , $Di_{pa}=Bia_{p}^{ a} Dm_{aa} \quad(5.2.1)$

и для нового:

$Bip_{a}^{ p}=Di_{ap} Lm^{pp}$ , $Di_{ap}=Bip_{a}^{ p} Dm_{pp} \quad(5.2.2)$

Здесь $Lm^{aa}$ — лапласовский (ЛМТ), а $Dm_{aa}$ — дистанционный (ДМТ) метрические тензоры исходного базиса. Соответственно $Lm^{pp}$ и $Dm_{pp}$ — метрические тензоры нового базиса.

В задаче перехода от одного базиса к другому требуется определить метрические тензоры нового базиса, если заданы тензоры исходного и дистанционный тензор преобразования.

Обратные матрицы перехода

Матрицы перехода $Di_{pa}$ и $Bia_{p}^{a}$ обратимы при условии отличного от нуля детерминанта матрицы перехода:

$Det(Di_{pa})\ne 0$ или $Det(Bia_{p}^{ a})\ne 0$

Нулевой детерминант матрицы преобразования означает ортогональность базисов. В ортогональном базисе невозможно выразить метрику проекций (ниже поясним о чем речь). Будем считать базисы неортогональными. Тогда обратные матрицы перехода выражаются через прямые следующим образом:

$Li^{ap}=(Di_{pa})^{-1}=(Bia^{a}_{ p} Dm_{aa})^{-1}=Lm^{aa} Bia_{a}^{ p} \quad(5.3.1)$

$Bia_{a}^{ p}=(Bia^{a}_{ p})^{-1}=(Di_{pa} Lm^{aa})^{-1}=Dm_{aa} Li^{ap}\quad(5.3.2)$

Матрица $Bia_{a}^{ p}$ — представляет собой би-координаты вершин старого базиса $a$ относительно вершин нового $p$ . То есть обращение би-координат дает взаимные би-координаты.

Матрица $Li^{ap}$ — это лапласовский тензор преобразования базиса (ЛТП). Согласно определению — является инвариантом, то есть не зависит от базисов. Ее структура аналогична структуре лапласовского метрического тензора (ЛМТ):

$Li^{ap}=\begin{pmatrix} D(a,p) & sa^{p} \\ sp^{a} & L^{ap} \end{pmatrix} \quad(5.4)$

Здесь главный минор $L^{ap}$ — это симметричный лапласиан. В окаймлении барицентрические координаты обратных проекций центров сфер двух базисов (симплексов). Центр сферы старого базиса выражен в барицентрических координатах нового — $sa^{p}$ , а центр нового в координатах старого — $sp^{a}$ .
Что понимается под «обратными проекциями» центров, будет пояснено далее.

В углу лапласовского тензора находится скаляр $D(a,p)$ . Его значение отражает скалярное произведение двух базисов — нового и старого. Чтобы раскрыть его смысл, рассмотрим две ситуации — 1) базисы принадлежат одному и тому же пространству и 2) базисы принадлежат разным пространствам.

Скалярное произведение базисов одного пространства — взаимная степень сфер

В общем пространстве скалярное произведение базисов выражается через квадраты радиуса описанных сфер ( $rs_a$ и $rs_p$ ) и дистанцию между центрами данных сфер ( $d_{ap}=|Oa, Op|$ ):

$D(a,p) = (rs_a + rs_p - d_{ap})/2 \quad(5.5)$

Данная формула подобна выражению для скалярного произведения векторов с общей вершиной (3.8). Поэтому можно считать соотношение (5.5) определением скалярного произведения гиперсфер или симплексов, принадлежащих одному пространству.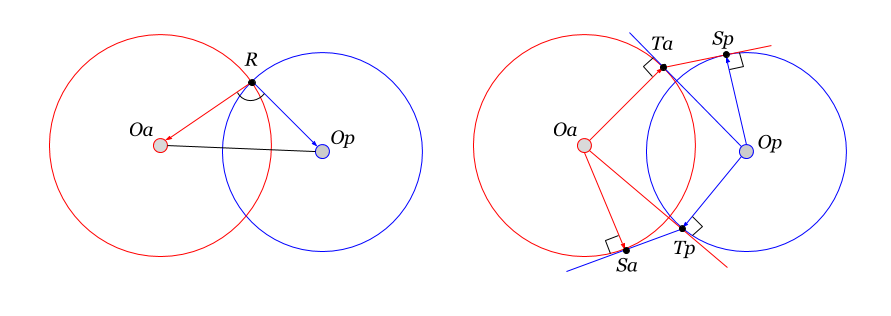

На рисунке показана геометрическая интерпретация скалярного произведения окружностей (2-мерных сфер). Слева — определение через скалярное произведение векторов $\vec{R \space Oa}$ и $\vec{R \space Op}$ . Если окружности пересекаются, то у них есть общая точка, из которой можно направить два вектора в сторону центров окружностей.

Скалярное произведение сфер можно определить через их взаимные степени (показано на рисунке справа). Геометрическое определение степени точки дано во 2-й части. Согласно (2.9) степень точки $m_p$ относительно сферы выражается через дистанцию от точки до сферы $r_p$ и радиус сферы $rs$ :

$m_p = r_p - rs \quad(2.9)$

Можно обобщить данное определение, если вместо точки использовать другую окружность (в общем случае сферу). Тогда взаимной степенью двух сфер $a$ и $p$ является следующая скалярная величина $M(a,p)$ :

$M(a,p) = d_{ap} - rs_a - rs_p \quad(5.6)$

На правом рисунке показано построение точек, принадлежащих сферам, значение дистанции между которыми равно взаимной степени сфер:

$M(a,p) = |Ta, Sp| = |Tp, Sa|$

По своим свойствам взаимная степень сфер обобщает свойства степени точки, то есть определяет взаимное расположение сфер. Если сферы находятся вне друг друга, то их взаимная степень положительна, если пересекаются — отрицательна.

Под пересечением здесь понимается ситуация, при которой точки касания $Ta$ (или $Tp$ ) находятся внутри сферы $p$ (или $a$ соответственно) (на рисунке взаимная степень сфер положительна). Возможно, что знак взаимной степени сфер связан с положением их центров относительно радикальной оси — если по разные стороны, то положительна, если по одну, то отрицательна (требует проверки).

Тогда скалярное произведение (5.5) — это взаимная полустепень сфер (и наоборот). Напомним (2.10), что под полустепенью понимается степень, деленная на (-2):

$D(a,p) = -M(a,p)/2 = M2(a,p) \quad(5.5')$

Если вершины сфер совпадают ( $d_{ap}=0$ ), то их полустепень (и скалярное произведение) будут равны среднему радиусу сфер:

$D(a,p, d_{ap}=0) = (rs_a + rs_p)/2 \quad(5.7)$

Если радиус одной из сфер нулевой, то формула (5.6) совпадает с определением степени точки (2.9). Таким образом можно определить полустепень точки как скалярное произведение точки и сферы (или соответствующего ей симплекса). Если радиус сферы равен нулю, то получаем скалярное произведение двух точек. Согласно (5.5) оно равно полудистанции между точками: $D(a,p) = d2_{ap}$ . К такому выводу мы уже приходили во 2-й части.

Скалярное произведение базисов разных пространств

Если базисы принадлежат разным пространствам, то геометрическая интерпретация их скалярного произведения (взаимной нормы базисов) $D(a,p)$ усложняется. Приведем вначале алгебраические тождества. Они аналогичны подобным для составляющих лапласовского тензора, приведенных в первой части.

Скалярное произведение базисов может выражено через отношение детерминантов дистанционной матрицы перехода и ее главного минора (см. 5.1.1):

$D(a,p) = det(Di_{pa})/det(D2_{pa}) \quad(5.8.1)$

Связь взаимной нормы базисов и барицентрических координат обратных проекций их центров сфер:

$D(a,p) 1_a = sa^{p} D2_{pa} \quad(5.8.3)$ — для вершин базиса $a$ .

$D(a,p) 1_p = D2_{pa} sp^{a} \quad(5.8.2)$ — для вершин базиса $p$ .

Разберемся, что такое обратная проекция точки. Допустим, что у нас есть точка $Tp$ , принадлежащая базису $p$ . Тогда ее обратной проекцией на базис $a$ будет такая точка $Tp^{(a)}$ , что перпендикуляр, опущенный из нее на базис $p$ , пересекается с ним в исходной точке $Tp$ .

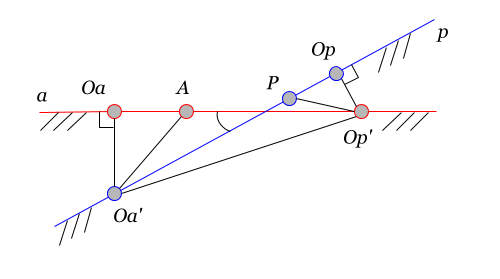
На рисунке обратной проекцией точки $Op$ на пространство $a$ является точка $Op'$ , а обратной проекцией точки $Oa$ на пространство $p$ — точка $Oa'$ . Точки $Oa$ и $Op$ — это центры сфер базисов $a$ и $p$ соответственно.

Понятие обратной проекции применимо также к радиусам сфер. Радиус при обратной проекции становится больше исходного (в отличие от прямой проекции). На рисунке дистанция $rs_a=|Oa,A|$ — это радиус сферы базиса $a$ . Его обратной проекцией на базис $p$ будет дистанция:
$rs^{(p)}_{a}=|Oa',A|=rs_a+|Oa,Oa'|$ .
Соответственно обратной проекцией радиуса базиса $p$ $rs_p=|Op,P|$ на базис $a$ будет дистанция
$rs^{(a)}_{p}=|Op',P|=rs_p+|Op,Op'|$ .
Обозначая дистанцию между обратными проекциями центров как $d'_{ap}=|Oa', Op'|$ , получаем следующее выражение для скалярного произведения базисов разных пространств:

$D(a,p) = (rs^{(p)}_{a} + rs^{(a)}_p - d'_{ap})/2 \quad(5.9)$

Видим, что по форме оно совпадает со взаимной нормой базисов одного пространства (5.5), но вместо дистанций используются их обратные проекции на взаимный базис. Если базисы принадлежат одному пространству, то угол между пространствами становится нулевым, и формула (5.9) переходит в (5.5).

Все приведенные формулы применимы также и к пространству графа. В графе нет описанных сфер (базиса), но есть связность. Тогда скалярное произведение базисов графа должно отражать их взаимную связность. Но вопрос интерпретации данного скаляра (взаимной нормы подграфов) требует исследований.

Расчет нового базиса

Здесь также рассмотрим две ситуации: 1) новый и старый базис принадлежат одному и тому же пространству и 2) принадлежат разным пространствам. Первый случай как правило относится к обычному геометрическому пространству (при смене базиса тут редко меняется его пространство), второй — к пространству графа.

Определить принадлежность точки (вершины) пространству базиса можно по норме точки в данном пространстве. Если равна нулю, то точка принадлежит данному пространству.

Единое пространство базисов

Для получения дистанционного метрического тензора (ДМТ) в новом базисе $Di_{pp}$ необходимо умножить ди-матрицу перехода $Di_{pa}$ на би-матрицу (перехода) $Bia^{a}_{p}$ . Полученная матрица будет совпадать с определением матрицы взаимных норм $N_{pp}$ (см. 4.4.2 в предыдущей части). Таким образом если пространства базисов совпадают, то матрица норм вершин нового базиса относительно старого — это и есть дистанционный метрический тензор нового базиса:

$Dm'_{pp}=N_{pp}=Di_{pa} Bia^{a}_{p}=Di_{pa} Lm^{aa} Di_{ap} \quad(5.10.1)$

Мы пометили данный ДМТ штрихом, чтобы помнить об условии общего пространства базисов. Лапласовский метрический тензор (ЛМТ) нового базиса можно получить обращением ДМТ:

$Lm'^{pp}=(Di_{pa} Bia^{a}_{p})^{-1}=Bia^{p}_{ a}Li^{ap} \quad(5.10.2)$

Координаты точки в новом базисе могут быть выражены через координаты в старом и матрицы перехода. Ди-координаты $di_{p}$ :

$di_{p} = Di_{pa} bi^a = Bia_{p}^{a} di_a \quad(5.11.1)$

Би-координаты точки в новом базисе $bi^p$ :

$bi^{p} = Bia^{p}_{a} bi^a = Li^{pa} di_a \quad(5.11.2)$

Все приведенные выражения аналогичны формулам изменения координат и в обычных (векторных) системах координат. В пределах общего пространства использование точечного базиса аналогично использованию векторного.

Пример преобразования базиса

На КДПВ показан основной базис $a$

из 3-х вершин (A, B, C) и новый базис $p$

, образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
\begin{array}{c | c c c c}
Dm_{aa} & * & A & B & C \\
\hline
* & 0 & 1 & 1 & 1 \\
A & 1 & 0 & -4.5 & -8 \\
B & 1 & -4.5 & 0 & -12.5 \\
C & 1 & -8 & -12.5 & 0 \\
\end{array}
Звездочкой обозначена скалярная компонента. Значение ЛМТ можно получить обращением ДМТ.

Дистанционную матрицу перехода считаем заданной. Ее вид в ди-координатах:
\begin{array}{c | c c c c}
Di_{pa} & * & A & B & C \\
\hline
* & 0 & 1 & 1 & 1 \\
P & 1 & -1.0 & -2.5 & -13.0 \\
Q & 1 & -6.5 & -2.0 & -6.5 \\
R & 1 & -12.5 & -2.0 & -20.5 \\
\end{array}

Значения би-координат матрицы перехода получаем по формуле (5.2.1):
\begin{array}{c | c c c c}
Bia_{p}^{a} & * & A & B & C \\
\hline
* & 1 & 0 & 0 & 0 \\
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \\
Q & 2.0 & -0.5 & 1.0 & 0.50 \\
R & -5.0 & -0.(6) & 1.(6) & 0.0 \\
\end{array}
Скалярной компонентой (значения первого столбца) би-координат являются полустепени точек. Сумма барицентрических компонент равна 1.

Лапласовский тензор преобразования (5.3.1):
\begin{array}{c | c c c c}
Li^{ap} & * & P & Q & R \\
\hline
* & 2.15 & 0.30 & 1.15 & -0.45 \\
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \\
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \\
C & -0.025 & -0.05 & 0.10 & -0.05 \\
\end{array}
Вектор $[0.30, 1.15, -0.45]$ — это барицентрические координаты центра сферы старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор $[0.058(3), 0.9(6), -0.025]$ — наоборот, барицентрические координаты центра описанной сферы симплекса PQR относительно вершин старого базиса.

Используя (5.10.1), получаем значение ДМТ в новом базисе:
\begin{array}{c | c c c c}
Dm'_{pp} & * & P & Q & R \\
\hline
* & 0 & 1 & 1 & 1 \\
P & 1 & 0 & -6.5 & -8.5 \\
Q & 1 & -6.5 & 0 & -4.0 \\
R & 1 & -8.5 & -4.0 & 0 \\
\end{array}

Базисы в разных пространствах

Если базисы находятся в разных пространствах, то формула (5.10.1) будет давать неверные значения полудистанций между вершинами нового базиса. В предыдущей части было показано, что в общем случае для нахождения правильных дистанций между вершинами необходимо к матрице норм прибавить фундаментальную матрицу $F_{pp}$ (4.5):

$D2_{pp} = N_{pp} + F_{pp} \quad(4.5, 5.12)$

Следовательно, при преобразовании базиса к базису из другого пространства необходимо наряду с матрицами перехода задать фундаментальную матрицу нового базиса (относительно исходного).

Если мы имеем дело с обычным геометрическим пространством, то для задания фундаментальной матрицы полезно вспомнить ее геометрический смысл (см. 4.6.1). Элемент фундаментальной матрицы — это скалярное произведение векторов, направленных к вершинам из их проекций на пространство базиса. В частном (но практически важном) случае общего надпространства элемент фундаментальной матрицы вычисляется как произведение расстояний от заданных точек до пространства базиса.

Скалярное произведение обратных проекций

В пространстве графа значения фундаментальной матрицы можно получить через матрицу смежности между старым и новым базисом $C^{pa}$ . Элементами данной матрицы является вес связей между вершинами двух базисов. Если матрица известна и обратима, то можно получить обратную матрицу смежности:

$H_{ap} = (C^{pa})^{-1} \quad(5.13.1)$

Полученная матрица (как и матрица смежности) является инвариантом — ее значения не зависят от выбора базиса. Значения элементов матрицы $H_{ap}$ отражают скалярное произведение обратных проекций между вершинами двух базисов. На рисунке представлена поясняющая схема.

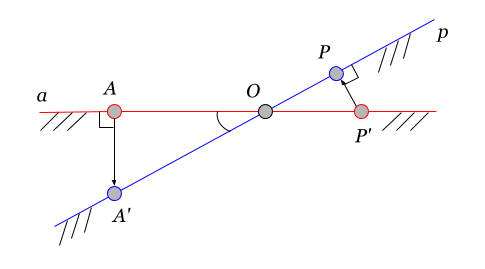
Здесь точка A принадлежит базису $a$ , а точка P — базису $p$ . Штрихами помечены обратные проекции точек на смежный базис. Тогда значение элемента матрицы — это скалярное произведение векторов $\vec{AA'}$ и $\vec{P'P}$ :

$H_{AP} = \vec{AA'} \cdot \vec{P'P} \quad(5.13.2)$

Можно выразить данное соотношение через расстояния от вершин до гиперплоскости пересечения пространств (на рисунке — точка O) и угол между пространствами $\alpha$ :

$H_{AP} = |OA| |OP| \sin(\alpha)^2/\cos(\alpha) \quad(5.13.2')$

Из формулы (5.13.2') видно, что если базисы ортогональны $cos(\alpha)=0$ , то элементы скалярного произведения обращаются в бесконечность.

Итоговые формулы преобразования базисов

Удобно привести размерность матрицы скалярных произведений проекций $H_{ap}$ к размерности остальных матриц перехода, окаймив ее нулями. Тогда фундаментальная матрица базиса $p$ определяется как

$F_{pp} = Bia_p^a H_{ap} \quad(5.14)$

Объединяя все вместе, получаем конечное выражение для дистанционного метрического тензора (ДМТ) нового базиса $p$ :

$Dm_{pp} = N_{pp} + F_{pp} = Bia_{p}^{a} W_{ap}=Di_{pa} Lm^{aa} Di_{ap} + Di_{pa} Lm^{aa} H_{ap} \quad(5.15.1)$

Симметричным образом выражается исходный базис при заданных матрицах преобразования:

$Dm_{aa} = N_{aa} + F_{aa} = W_{ap} Bip^{p}_{a}=Di_{ap} Lm^{pp} Di_{pa} + H_{ap} Lm^{pp} Di_{pa} \quad(5.15.2)$

Здесь $Bia^{a}_{ p}$ и $Bip^{p}_{a}$ — би-координаты матриц перехода (5.2.1) и (5.2.2). $W_{ap}$ — общая дистанционная матрица преобразования:

$W_{ap} = Di_{ap} + H_{ap} \quad(5.16)$

Данная матрица является инвариантом, состоит из двух частей — дистанционного тензора преобразования $Di_{ap}$ и добавки, связанной с некомпланарностью пространств базисов — матрицы скалярных произведений проекий $H_{ap}$ .

Лапласовский тензор базисов получается обращением ДМТ (5.15). Задача определения связи базисов решена.

Тяжелая формульная часть серии в целом завершена. Приведены основные понятия и тождества. Точечные базисы — это полезный и мощный инструмент для различных прикладных задач. В конце мы подведем итоги серии с выделением основных результатов.

В следующей (заключительной) статье немного расслабимся и пофилософствуем. Применим дистанционные координаты к разложению составных чисел на простые. При всей тривиальности примера в нем есть любопытный момент, связанный с понятием псевдоевклидовости пространства.