Геометрия данных 3. Скалярное произведение векторов
Любые системы координат — лишь подпорки для описания «положения вещей». Поэтому важно отличать понятия, связанные с системой координат и независимые от нее — инварианты. В данной статье рассмотрим один из таких инвариантов — скалярное произведение векторов. Одна из целей серии (начало здесь) — обновить сложившиеся стереотипы, поэтому постараемся выйти за рамки привычного геометрического смысла.

Схема установки для исследования методом сопротивления: A и B — питающие заземления; M и N — измерительные заземления; 1 — измерительный прибор (из книги «Электроразведка», Якубовский Ю. B., M., 1980).
На рисунке показана схема измерения скалярного произведения векторов и
на грунте.
Тензоры координат
Напомним, что пространства точек и пространство векторов — это два разных пространства. В точечном базисе это различие выражено в структуре координат — ди-координаты векторов имеют нулевую скалярную компоненту, а би-координаты векторов являются балансовыми (сумма их компонент равна нулю).
Если координаты точек пространства собрать в список (массив), то получим матрицу. Строки данной матрицы будут соответствовать точкам пространства, а столбцы — компонентам координат, то есть базовым точкам. Обозначим массив ди-координат точек как . Индекс
означает точку пространства, а индекс
— точку базиса. Метрический тензор определяется на вершинах базиса, поэтому при «жонглировании индексами» (переходе от ди-координат к би-координатам
и обратно) индекс точки положение не меняет:
и
Взаимные нормы точек пространства будут матрицей:
Как показано в предыдущей части (см. 2.17.2, 2.17.3), нормы точек связаны с дистанцией до пространства базиса, и по этой причине не являются инвариантами.
Нормы векторов
Вектор представляет собой разность координат двух точек, соответственно его тензор имеет два индекса точек и один индекс базиса:
Здесь определены массивы координат ди- и би-
координат векторов соответственно. Тензоры координат антисимметричны относительно перестановок индексов точек:
.
Дистанция между точками и
будет двумерной матрицей
норм векторов:
В (3.4) учтено, что правило свертки индексов применяется только к индексам разного уровня.
Дистанция между точками является инвариантом — не зависит от выбора базиса.
Скалярное произведение векторов
Под скалярным произведением понимается свертка координат векторов по индексу базиса. Результат свертки двух векторов — скаляр, не зависит от выбора системы координат (инвариант). Если и
— это два неких вектора, то их скалярное произведение в тензорной форме можно записать как:
Выражение аналогично скалярному произведению координат точек, но тут речь о перемножении векторов. Далее будем называть также результат скалярного произведения векторов взаимной нормой векторов, чтобы отличать понятие операции скалярного произведения (свертки любых координат) от результата ее применения к векторам.
Поскольку умножать можно любые векторы пространства, то в общем случае выражение для взаимной нормы векторов представляет собой тензор:
Индексы задают координаты одного вектора, а индексы
— другого.
Связанные пары — три вершины, теорема косинусов
Согласно определению вектор можно представить как сумму других векторов, начало и конец которых совпадают:
Если теперь раскрыть норму вектора , подставив (3.7) в (3.4), то получим выражение для взаимной нормы (скалярного произведения) векторов
и
:
Здесь — норма вектора
, совпадает с дистанцией между точками i и k.
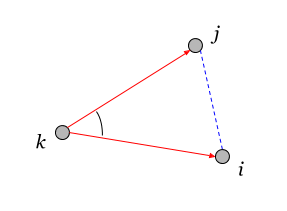
Формула (3.8) — это обычная теорема косинусов для треугольника. Здесь векторы, между которыми определена взаимная норма, имеют общую точку k, (смежные векторы).
Квадрат скалярного произведения на 3-х вершинах связан с площадью образуемого ими треугольника (формула Герона):
Независимые пары — четыре вершины
В общем случае взаимная норма может быть определена для векторов, не имеющих общих точек. Вывод формулы аналогичен (3.8), только вместо одной промежуточной точки используем две. Получаем:
Это общая формула скалярного произведения векторов (взаимных норм).
Геометрически значение взаимной нормы отражает произведение косинуса угла между векторами на их длину. Порядок индексов важен — задает направление векторов.
Выражения вида (3.10) (четыре слагаемых — два положительных, два отрицательных) встречаются в разных разделах математики. Его присутствие обычно означает, что скорее всего есть и пара векторов, скалярное произведение которых задает структуру данного выражения.
Симметрия тензора норм векторов
Перечислим свойства тензора взаимных норм .
1) Очевидно, что он антисимметричен относительно перестановки индексов или
:
2) Не зависит от перестановки векторов:
3) Существует только две независимых нормы на заданных 4-х точках ввиду тождества:
Знатоки математики должны увидеть в формуле (3.11.3) первое (алгебраическое) тождество Бьянки. Из чего можно сделать вывод, что структуры тензора кривизны (Римана) и тензора взаимных норм векторов — подобны.
4) Векторная норма на 4-х вершинах может быть выражена через разность норм на 3-х вершинах:
Это полезное тождество, которое нам еще понадобится.
Скалярное произведение векторов на графах
На графах скалярное произведение векторов — это сопоставление двух пар вершин. Допустим, задан граф с известной матрицей смежности, а, значит, и лапласианом . Тогда скалярным произведением между вектором разности узлов
с одной стороны и вектором на узлах
с другой является значение кофактора 2-го порядка, деленное на скалярный потенциал лапласиана (алгебраическое определение):
Напомним, что кофактором называется определитель минора квадратной матрицы (с учетом знака). Скалярный потенциал
— это кофактор 1-го порядка от лапласиана (см. (1.12) из первой статьи). То есть для получения значения взаимной номы векторов на графе необходимо из матрицы лапласиана удалить столбцы, соответствующие одному вектору (в формуле это i-й и j-й столбцы), и строки, соответствующие другому (k и l), после чего разделить определитель получившегося минора на скалярный потенциал
.
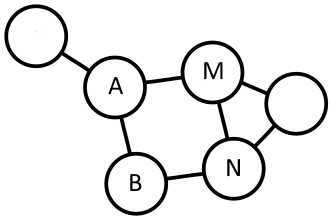
Если удаляемые столбцы и строки лапласиана — одни и те же, то получим значение эффективного сопротивления между узлами графа (резистивную дистанцию). Таким образом скалярное произведение векторов связано с понятием обобщенного сопротивления в электрической цепи.
Для измерения такого («кажущегося») сопротивления источник тока (напряжение) прикладывается к одним узлам (A и B), а разность потенциалов измеряется между другими (M и N). (Это основной метод измерений в электрометрии — см. КДПВ). Взаимная норма (скалярное произведение) векторов равна нулю, если внешняя разность потенциалов не приводит к разности потенциалов на измеряемом векторе.
В следующей статье разберем подробнее, почему отношение заданной и измеряемой разностей потенциалов узлов связано со скалярным произведением векторов.
Обращение минора лапласиана
Подматрицу значений взаимных норм можно получить обращением минора лапласиана. Обозначим лапласиан, из которого удалены a-я строка и b-й столбец как . Тогда имеет место тождество
Формула (3.12.2) — один из способов получить дистанционную матрицу по заданному лапласиану. Удаляем из лапласиана графа какой-либо из узлов (пусть будет a) и обращаем. Получаем матрицу взаимных норм векторов . Значение индекса a фиксировано — базовый узел. Матрица
представляет собой скалярные произведения векторов, начало которых находится в базовом узле a, а конец пробегает по точкам пространства.
Для восстановления дистанционной матрицы добавим к множеству узлов базовый (удаленный из лапласиана), то есть просто расширим матрицу
нулевой строкой и столбцом. Далее применяем к матрице преобразование дистанции:
.
В результате получим дистанционную матрицу .
Квадрат скалярного произведения, матрица Якоби
Если в графе изменить значение проводимости ребра (элемент лапласиана), то очевидно, что изменятся и все дистанции между вершинами (нормы векторов) . При увеличении проводимости дистанции должны сократиться (уменьшиться). Подарок богов в том, что можно оценить изменение дистанций не только качественно, но и количественно. Обозначим производную матрицы дистанций по лапласиану как
Тензор — это матрица Якоби, то есть выражение изменений значений дистанционной матрицы
при изменении значений лапласиана
. Оказывается, что данный тензор выражается через квадрат скалярного произведения векторов (квадрат норм):
Круто, что сущности не множатся. Вариация лапласиана связана с вариацией дистанционной матрицы через известное понятие скалярного произведения векторов. Этим подчеркивается роль данного тензора. Кроме того, тензор квадратов скалярного произведения можно обращать.
Тензор квадросвязности вершин
Выражение (3.13) можно представить в таком эквивалентном виде:
Данную формулу можно трактовать как отклик на воздействие
. Тензор
играет роль передаточной функции (реакции на воздействие).
Возможна и обратная ситуация, при которой воздействие и отклик меняются местами. Прямая и обратная передаточные функции связаны соотношением:
Снова удача — тензор можно выразить через лапласиан:
Если важен тензор взаимных норм, то и тензор должен быть не менее значим. Назовем его тензором квадросвязности и кратко рассмотрим его свойства.
Свойства квадросвязности вершин
Значения тензора определены через значения лапласиана для 4-х вершин. Будем считать данные вершины вершинами графа. Допустим, что все 4 вершины различны:
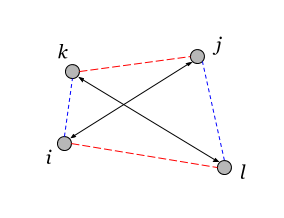
Здесь векторами обозначены пары вершин, между которыми считается квадросвязность. Пары имеют отличную от нуля квадросвязность только тогда, когда их вершины попарно связаны (необходимые связи показаны на рисунке одинаковым цветом). Если все связи в графе положительны, то квадросвязность между разными вершинами также всегда больше или равна нулю.
Если пары имеют общую вершину, то смысл квадросвязности меняется. Это связано с тем, что диагональные элементы лапласиана не равны нулю (как в дистанционной матрице), а отражают общую связность (проводимость) узла.
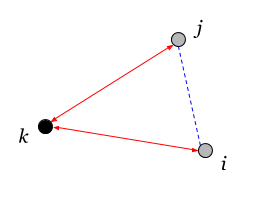
Пары вершин могут совпадать — диагональные элементы тензора квадросвязности.
Здесь характеризует связь двух узлов i и j. Считается как сумма произведения их суммарной проводимости (степени вершины)
и квадрата связи между узлами
.
Несмотря на то, что формально для тензора могут вычисляться элементы вида
(одна из пар вырождена), данные (вырожденные) элементы являются линейно-зависимыми от остальных. Могут быть вычислены через сумму тензора по одному из индексов пары:
___
На этом пока все. Мы определили инвариант скалярного произведения векторов на 4-х вершинах, показали его основные свойства. В следующей статье рассмотрим пространство графа, определим на нем точечный базис и разберемся с его возможностями.
