Генетическое программирование («Yet Another Велосипед» Edition)

Давайте на время отвлечемся от очередного «языка-убийцы C++», ошеломляющих синтетических тестов производительности какой-нибудь NoSQL-ой СУБД, хайпа вокруг нового JS-фреймворка, и окунемся в мир «программирования ради программирования».
Предисловие
Март начинался для меня с чтения статей про то, что Хабр уже не торт. Судя по отклику, тема была вскрыта наболевшая. С другой стороны, мне удалось кое-что для себя вынести из этого: «вы и есть Сопротивление», если вы это читаете — вы и есть Хабр. И сделать его интереснее (или хотя бы разнообразнее, отойти от наметившейся тенденции на агрегацию рекламных постов, околоализарщины и корпоративных блогов) можно только силами рядовых пользователей. У меня как раз имелся на тот момент небольшой проект, хоть и требующий серьезной доработки, о котором мне захотелось рассказать. И я решил — за месяц (наивный! ) напишу статью. Как мы видим, сейчас уже середина конец апреля начало мая май в самом разгаре, винить в этом можно как мою лень, так и нерегулярность свободного времени. Но всё же, статья увидела свет! Что интересно, пока я трудился над статьей, уже успели выйти две похожие: Что такое грамматическая эволюция + легкая реализация, Символьная регрессия и еще один подход. Не будь я таким слоупоком, можно было вписаться и объявить месяц генетических алгоритмов :)
Да, я осознаю в полной мере, что на дворе 2016 год, а я пишу такой длиннопост. Ещё и рисунки выполнены в стиле «курица лапой» пером на планшете, с шрифтами Comics Sans для гиков xkcd.
Введение
Некоторое время назад на ГТ появилась интересная статья, с, что характерно, ещё более интересными комментариями (а какие там были словесные баталии об естественном отборе!). Возникла мысль, что если применить принципы естественного отбора в программировании (если быть точнее, то в метапрограммировании)? Как вы можете догадаться, эта мысль в итоге и привела меня к переоткрытию давно существовашей концепции генетических алгоритмов. Бегло изучив матчасть, я с энтузиазмом ринулся экспериментировать.
Но давайте обо всём по порядку.
Ликбез
Практически все принципы, лежащие в основе генетических алгоритмов, почерпнуты из природного естественного отбора — популяции через смену поколений адаптируются к условиям окружающей среды, наиболее приспособленные из них становятся доминирующими.
Как с помощью генетических алгоритмов решать задачи? Вы удивитесь, как всё просто работает в нулевом приближении:
Теперь WE NEED TO GO DEEPER. Первое приближение:
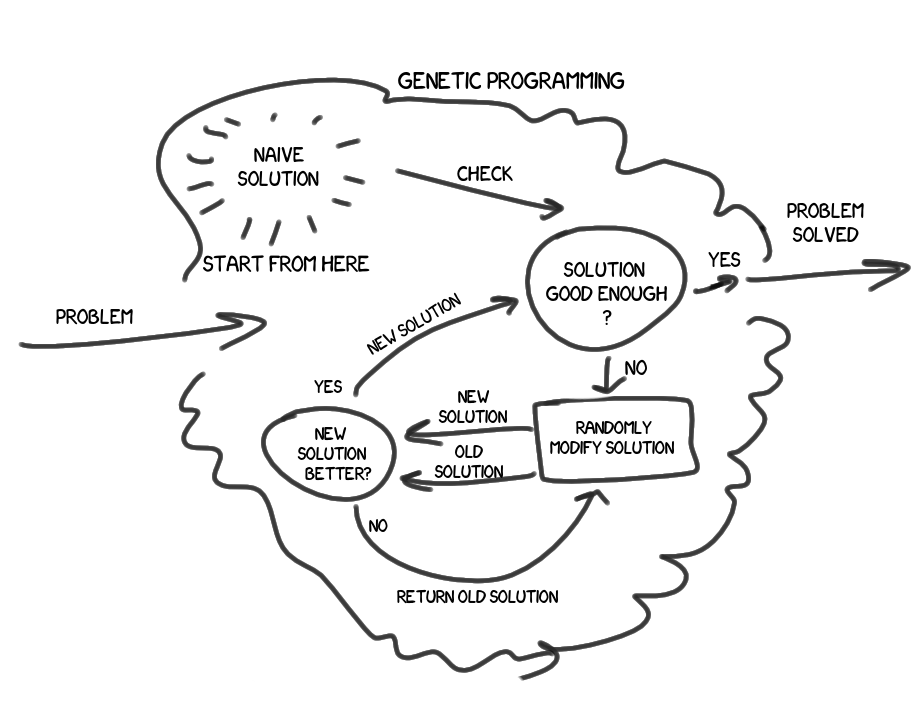
Значит, у нас есть задача\проблема, мы хотим найти её решение. У нас есть какое-нибудь базовое, плохенькое, наивное решение, результаты которого нас, скорей всего, не удовлетворяют. Мы возьмём алгоритм этого решения и немного изменим его. Натурально случайным образом, без аналитики, без вникания в суть проблемы. Новое решение стало выдавать результат хоть на капельку лучше? Если нет — отбрасываем, повторяем заново. Если да — ура! Удовлетворяет ли результат нового решения нас полностью? Если да — мы молодцы, решили задачу с заданной точностью. Если нет — берем полученное решение, и проводим над ним те же операции.
Вот такое краткое и бесхитростное описание идеи в первом приближении. Впрочем, думаю, пытливые умы оно не удовлетворит.
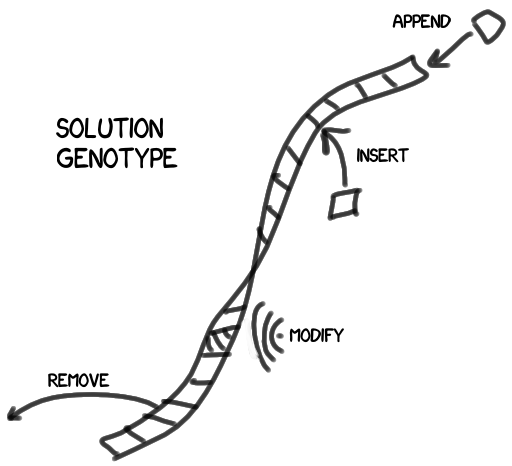
Для начала, как мы модифицируем решения?
Наше решение состоит из набора дискретных блоков — характеристик, или, если позволите, генов. Меняя набор, мы меняем решение, улучшая, или ухудшая получаемый результат. Я изобразил генотип как цепочку генов, но на практике это будет древовидная структура (не исключающая, впрочем, и возможности содержать цепочку в одном из своих узлов).
Теперь давайте рассмотрим основной цикл подробнее:
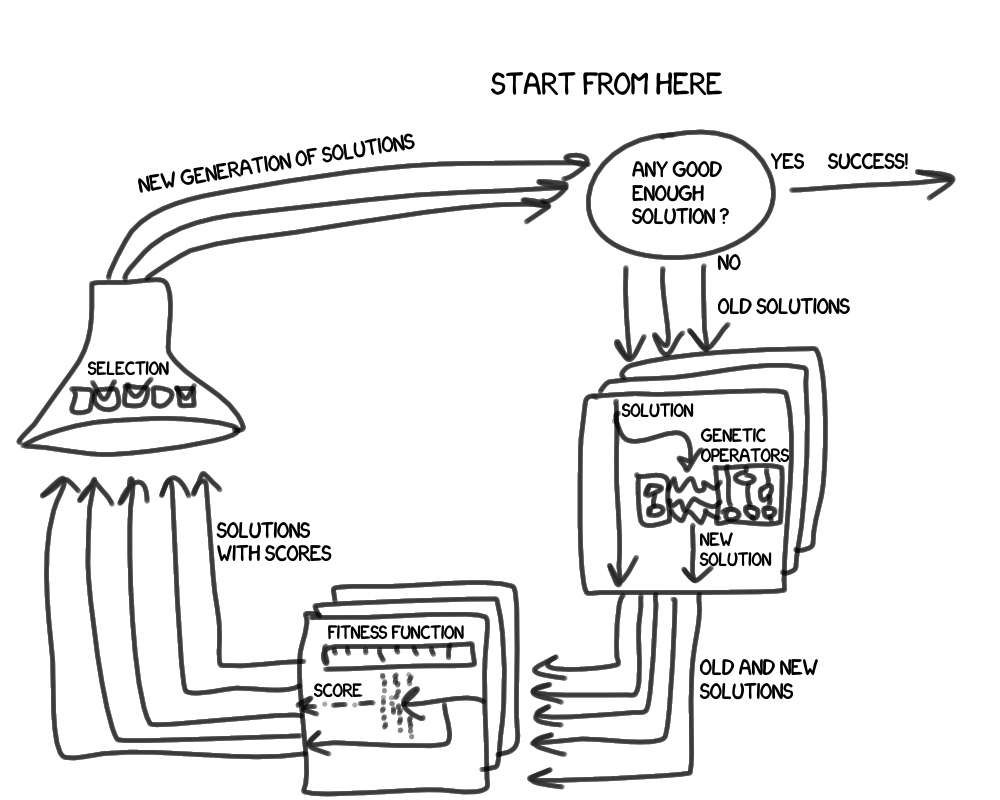
Что стало различимо во втором приближении? Во-первых, мы оперируем не одним, а группой решений, которую назовем поколение. Во-вторых, появились новые сущности:
- Генетические операции (да-да, извечная путаница с переводом, английское »operator» суть наше »операция») нужны чтобы получить новое решение на базе предыдущих. Обычно это скрещивание (случайное совмещение двух различающихся решений) и мутация (случайное изменение одного решения).
- Функция приспособленности (мне больше понравилось фитнесс-функция) нужна для оценки степени нашей удовлетворенности результатом решения.
Кому на ум пришло TDD?
В самом деле, когда если мы научимся легко писать тесты которые отвечают не только на вопрос, завалил ли наш код тест или нет, но и дают измеримую оценку, насколько он близко он подошел к успеху, мы станем на шаг ближе к самопишущимся программам. Не удивлюсь, если такие попытки уже были.
- Селекция описывает принципы отбора решений в следующее поколение.
Недостатки
Как бы многообещающе всё ни звучало, у обсуждаемого подхода к решению задач полно фатальных фундаментальных недостатков. Практикуясь, я споткнулся, наверное, обо все известные подводные камни. Самый главный, на мой взгляд, из них: плохая масштабируемость. Скорость роста затрат на вычисления в среднем превышает скорость роста входных данных (как в наивных алгоритмах сортировки). Об остальных недостатках я расскажу попутно далее.
Практика
Выбор языка
Был выбран Ruby. Этот язык относительно недавно заполнил в моих делах нишу, каковую традиционно занимал Питон, и он настолько меня очаровал, что я непременно решил познакомиться с ним поближе и заиметь побольше опыта. А тут такая возможность! Люблю убивать N (где N > 1) зайцев за раз. Не исключаю, что мой код может местами вызывать улыбки, если не фейспалмы у олдовых рубистов (нет, извините, но именно рУбистов, остальные варианты — троллинг).
Генотип
Первой мыслью было то, что раз в языке есть eval, то генотип решения может без каких-либо ухищрений строиться из произвольных символов (выступающих в роли генов), и на выходе мы будем иметь скрипт, интерпретируемый самим Ruby. Второй мыслью было то, что на эволюцию решений с такими высокими степенями свободы может уйти реально много лет. Так что я даже не шевельнул пальцем в этом направлении, и думаю, не прогадал. Можно попробовать данный подход лет этак через 30, если сохранится закон Мура.
Эволюция в итоге была заключена в достаточно жесткие рамки. Генами решения являются высокоорганизованные токены с возможностью вложенности (построения древовидной структуры).
В первом эксперименте, где мы будем говорить о решениях как математических выражениях, токены это константы, переменные, и бинарные операции (не знаю, насколько легитимен термин, в контексте проекта «бинарная операция» значит действие над на двумя операндами, например сложение).
Кстати, я решил частично оставить совместимость с eval, поэтому если запросить строковое представление токена (через стандартный to_s), то можно получить вполне удобоваримую строку для интерпретации. Например:
f = Formula::AdditionOperator.new(Formula::Variable.new(:x), Formula::IntConstant.new(5))
f.to_s # "(x+5)"
Да и нагляднее так.
Генетические операции
В качестве основного и единственного способа изменения генотипа решений я выбрал мутацию. Главным образом потому, что она проще формализуется. Не исключаю, что размножение скрещиванием могло бы быть эффективнее (а если судить на примере живой природы, то, похоже, так и есть), однако в её формализации кроется много подводных камней, и, скорей всего, накладываются определенные ограничения на саму структуру генотипа. В общем, я пошёл простым путем.
В разделах статьи, посвященных описанию конечных экспериментов, подробно расписаны правила мутации решений. Но есть и общие особенности, о которых хочется рассказать:
- Иногда (на самом деле часто) бывает, что лишь за один шаг мутации невозможно добиться улучшения результатов, хотя мутация идет, в целом, в верном направлении. Поэтому в фазе применения генетических операций решениям позволено мутировать неограниченное количество раз за ход. Вероятность выглядит так:
— 50% — одна мутация
— 25% — две мутации
— 12.5% — три мутации
— и т.д. - Бывает, за несколько шагов мутант может стать идентичным родителю, или разные родители получают одинаковых мутантов; такие случаи пресекаются. Более того, я вообще решил поддерживать строгую уникальность решений в рамках одного поколения.
- Иногда мутации порождают совершенно неработоспособные решения. С этим бороться аналитически крайне сложно, обычно, проблема вскрывается только в момент их оценки фитнесс-функцией. Я позволяю таким решениям быть. Всё равно бОльшая часть со временем исчезнет в результате селекций.
Фитнесс-функция
С её реализацией никаких проблем нет, но есть один нюанс: сложность фитнесс-функции растет практически наравне с ростом сложности решаемой задачи. Чтобы она была способна выполнять свою работу в разумные сроки, я постарался реализовать её настолько просто, насколько возможно.
Напомню, что генерируемые решения возвращают определенный результат на основе определенного набора входных данных. Так вот, подразумевается, что мы знаем, какой идеальный (эталонный) результат нужно получить на определенный набор входных данных. Результаты являются исчислимыми, а значит, мы способны выдать количественную оценку качества определенного решения, проведя сравнение возвращенного результата с эталонным.
Помимо этого, каждое решение обладает косвенными характеристиками, из которых я выделил, по моему мнению, основную — ресурсоемкость. В некоторых задачах ресурсоемкость решения бывает зависима от набора входных данных, а в других — нет.
Итого, фитнесс-функция:
- вычисляет насколько результаты решения отличаются от эталонных
- определяет, насколько ресурсоемко решение
В ранних прототипах я пробовал замерять затраченное на прохождение испытаний процессорное время, но даже при длительных (десятки миллисекунд) прогонах наблюдался разброс в ±10% времени на одно и то же решение, вносимый операционной системой, с периодическими выбросами +в 100–200%.
Так что в первом эксперименте ресурсоемкость вычисляется суммарной сложностью генотипа, а во втором подсчётом реально выполненных инструкций кода
Селекция
Каждое поколение содержит не более чем N решений. После применения генетических операторов, у нас максимум 2N решений, притом в следующее поколение пройдет, опять же, не больше N из них.
По какому принципу формируется следующее поколение решений? Мы на этапе, когда каждое из решений уже получило оценку фитнесс-функции. Оценки, разумеется, можно сравнивать друг с другом. Таким образом, мы можем отсортировать текущее поколение решений. Дальше видится логичным просто взять X лучших решений, и сформировать из них следующее поколение. Однако, я решил не останавливаться на этом, и включать в новое поколение также Y случайных решений из оставшихся.
Например, если X = Y, то чтобы решению пройти в следующее поколение, ему нужно оказаться среди 25% лучших, либо выкинуть 3 на трёхгранном кубике (если бы такой существовал). Достаточно гуманные условия, не так ли?
Так вот, включение случайно выживших в следующее поколение нужно для сохранения видового многообразия. Дело в том что подолгу держащиеся среди лучших похожие друг на друга решения выдавливают остальные, и чем дальше, тем быстрее процесс, а ведь зачастую бывает что доминирующая ветвь оказывается тупиковой.
Параметры X и Y, разумеется, являются настраиваемыми. Я прогонял тесты, как со случайными выжившими, так и без них, и доказал справедливость их добавления в алгоритм: в отдельных случаях (при поиске решений повышенной сложности), удавалось достичь более хороших результатов с их использованием (притом суммарная затрачиваемая на поиск решений мощность оставалась постоянной, например, X1 = 250, Y1 = 750 против X2 = 1000, Y2=0).
Условия победы
Тут кроется загвоздка: как понять, что пора заканчивать? Допустим, решение удовлетворяет нас по точности результатов, но как быть с трудоемкостью? Вдруг алгоритм сейчас поработает и выдаст решение по раскраске графов за O (n)? Утрирую конечно, но критерий остановки работы необходимо формализовать. В моей реализации выполнение алгоритма заканчивается, когда Top 1 решение не меняется определённое количество поколений (сокращенно R — rounds). Отсутствие ротации значит, что, во-первых, не нашлось альтернативного решения, которое бы смогло превзойти лучшее текущее решение; во-вторых, лучшее текущее решение не смогло породить улучшенную мутацию себя в течение заданного времени. Количество поколений, через которое наступает победа лучшего решения, обычно большое число — чтобы действительно убедиться в том, что эволюция не способна продвинуться дальше, требуется смена нескольких сотен (число варьируется в зависимости от сложности самой задачи) поколений.
К сожалению, несмотря на многочисленные предосторожности, случаи когда эволюция заходит в тупик всё же бывают. Это известная проблема генетических алгоритмов, когда основная популяция решений сосредотачивается на локальном оптимуме, игнорируя, в итоге, искомый глобальный оптимум. На это можно ответить игрой с параметрами: уменьшением квоты для победителей, увеличением квоты для случайных, и увеличением времени доминирования для победы, параллелизацией независимых друг от друга поколений. Но всё это требует мощностей\времени.
Конкретная реализация
Как принято, всё выложено на гитхабе (правда, пока без доков).
Теперь о том, что мы увидим в конкретно моей велосипеде реализации:
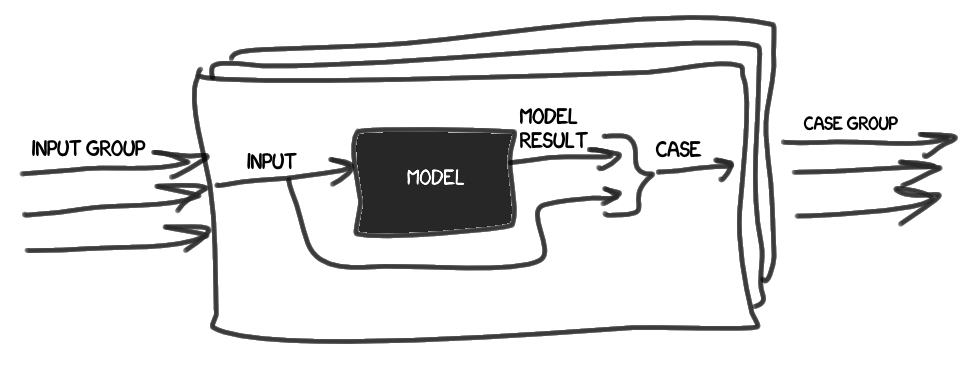
- Вводится понятие эталона (Model). Относимся к нему, как к чёрному ящику, с помощью которого, на основе набора входных данных (Input), можно получить эталонный результат(Model Result).
- Дело (Case) попросту содержит набор входных данных и эталонный результат.
-
Собираем набор дел (Case group) на основании совокупности входных данных (Input group).
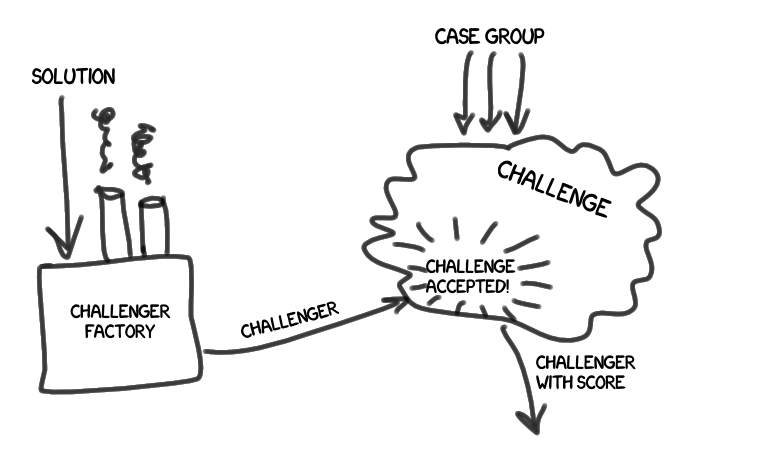
- Вызов (или испытание) (Challenge) это комплекс действий по прохождению сформированного ранее набора дел. На плечах испытания также работа по оценке результатов прохождения, и сравнению оценок.
-
У нас появляется претендент (Challenger), имеющий определенное решение (Solution). Претендент произносит сакраментальное »вызов принят! », и узнает свою степень пригодности (Score).
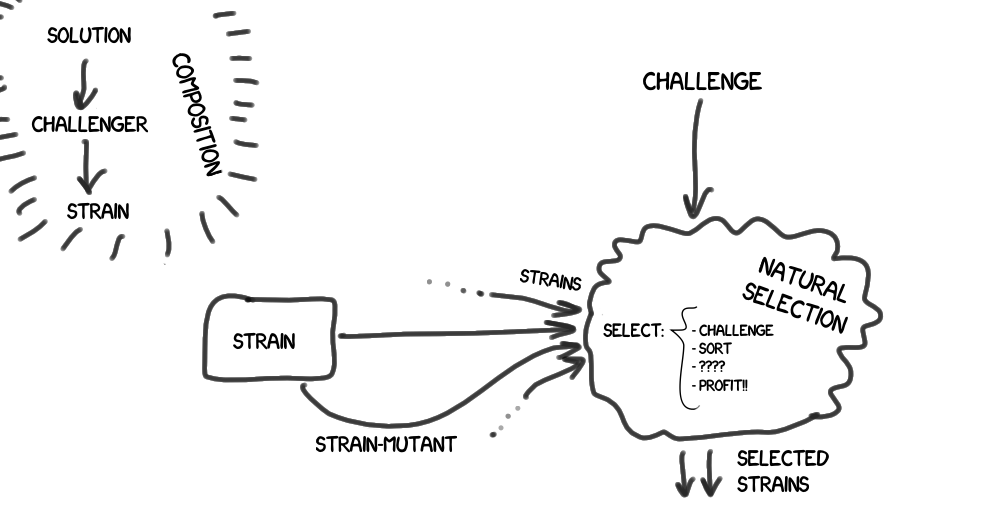
- В итоге у нас выстраивается цепочка композиции — решение(Solution — предоставляет решение определенного вида задач) → претендент(Challenger — проходит испытания) → штамм(Strain — участвуют в естественном отборе и эволюции(см.ниже))
-
Имеется естественный отбор (Natural Selection), который включает в себя испытание, и фильтрует поступающую к нему группу штаммов по заданным правилам.
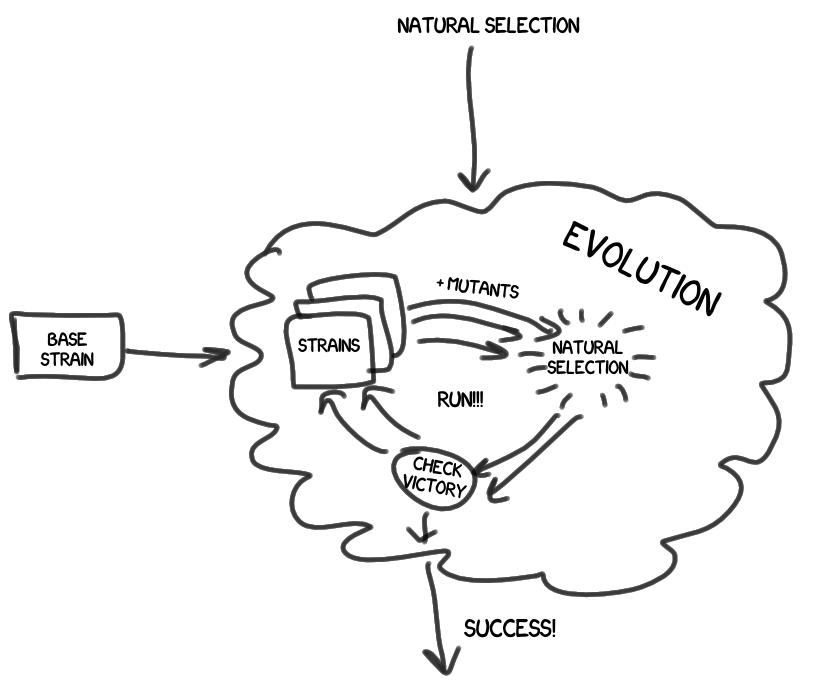
- На верхнем уровне располагается эволюция (Evolution), которая, включая в себя естественный отбор, управляет всем жизненными циклом штаммов.
- Результатом работы эволюции является штамм-победитель, которого мы чествуем как героя, а затем внимательно изучаем его, в том числе и его родословную. И делаем выводы.
Такова в общих чертах моя реализация генетического алгоритма. За счёт абстрактных классов (в Ruby, ага >_<), удалось написать в целом независимый от конкретной области задач код.
В последующих экспериментах дописывались нужные Input, Model, Solution, Score (что, конечно, немало).
Эксперимент Первый: Формулы
Вообще, вернее было назвать Эксперимент Первый: Арифметические выражения, но когда я выбирал имя для базового класса выражений, то, недолго думая, остановился на Formula, и дальше в статье я буду называть арифметические выражения формулами. В эксперименте мы вводим формулы-эталоны (та самая Model), содержащие одну или несколько переменных величин. Например:
x2 — 8*x + 2.5
У нас есть набор значений переменных (Input Group, ага), например:
- x = 0;
- x = 1;
- x = 2;
- …
- x = 255;
Решения (Solutions), которые мы будем сравнивать с эталонами, представляют из себя такие же формулы, но создаваемые случайно — последовательно мутирующие из базовой формулы (обычно это просто x). Оценкой (Score) качества решения является среднее отклонение результата от результата эталона, плюс ресурсоемкость решения (суммарный вес операций и аргументов формулы).
Мутация формул
Как было упомянуто ранее, токенами формул являются константы, переменные, и бинарные операции.
Как происходит мутация формул? Она затрагивает один из токенов, содержащихся в формуле, и может пойти тремя путями:
- grow — рост, усложнение
- shrink — уменьшение, упрощение
- shift — видоизменение с условным сохранением сложности
Вот таблица происходящего с разными типами формул при разных видах мутации:
| Формула → Мутация ↓ | Константа | Переменная | Бинарная операция |
|---|---|---|---|
| grow | становится переменной, или включается в новую случайную бинарную операцию (со случайным вторым операндом) | в новую случайную бинарную операцию (со случайным вторым операндом) | включается в новую случайную бинарную операцию (со случайным вторым операндом) |
| shrink | невозможно уменьшить, так что применяем к ней операцию shift | становится константой | вместо операции остается лишь один из операндов |
| shift | изменяет свое значение на случайную величину, может поменять тип (Float<->Int) | становится другой случайной переменной (если это допустимо в данном контексте) | либо операнды меняются местами, либо меняется вид операции, либо происходит попытка сокращения операции |
Примечание 1 Сокращение формул это попытка заранее произвести операции над константами, где это возможно. Например из »(3+2)» получить »5», а из »8/(x/2)» получить »(16/x)». Задача неожиданно оказалась настолько нетривиальна, что вынудила меня писать прототип решения с исчерпывающим юнит-тестом, и то, я не добился настоящего рекурсивного решения, достающего константы для сокращения с любой глубины. Разбираться в этом было увлекательно, но в какой-то момент мне пришлось остановить себя и ограничиться достигнутым решением, так как я слишком отклонился от основных задач. В большинстве ситуаций, сокращение и так полноценно работает.
Примечание 2 У мутации бинарных операций есть особенность, в силу того, что операции имеют вложенные в себя другие формулы-операнды. Мутировать и операцию, и операнды — слишком большое изменение для одного шага. Так что случайным образом определяется, какое событие произойдёт: с вероятностью 20% мутирует сама бинарная операция, с вероятностью 40% мутирует первый операнд, и с оставшейся 40% вероятностью, мутирует второй операнд. Не могу сказать, что соотношение 20–40–40 идеально, возможно следовало бы ввести корреляцию вероятности мутации операции в зависимости от их весов (фактически, глубины вложенности), но пока что работает так.
Результаты
Теперь ради чего, собственно, всё затевалось:
Первый эталон — простой полином:
x2 — 8*x + 2.5
X принимает значения от 0 до 255, с шагом 1
R = 64, X = 128, Y = 128
Прогоны выполняются по три раза, здесь отражен лучший результат из трёх. (Обычно все три раза выдают идентичные результаты, но изредка бывает, что мутации заходят в тупик и не могут достичь даже заданной точности)
Результаты поразили меня в самое сердце:) За 230 (включая те R раз, когда Top 1 не менялся) поколений было выведено такое решение:
(-13.500+((x-4)2))
Как вы помните, между один поколением допускается и более одной мутации.
x
(x-0)
((x-0)-0.050)
(0.050-(x-0))
(0.050-(x-1))
(x-1)
(x-1.000)
((x-1.000)--0.010)
((x-1.000)-0)
((x-1.000)-(1*0.005))
((x-1.000)/(1*0.005))
((x-1.020)/(1*0.005))
((x-1.020)/(0.005*1))
((x**1.020)/(0.005*1))
((x**1)/(0.005*1))
((x**1)/(0.005*(0.005+1)))
((x**1)/(0.005*(0.005+1.000)))
(x**2)
((x--0.079)**2)
((x-0)**2.000)
(((x-0)**2.000)/1)
(((x-0)**2)/1)
((((x-0)**2)-0)/1)
(((x-0)**2)-0)
(((x-0)**2)-0.000)
(((x-(0--1))**2)-0.000)
(((x-(0--2))**2)-0.000)
(((x-(0--2))**2)+0.000)
(((x-((0--2)--1))**2)+0.000)
(((x-((0--2)--1))**2)+-0.015)
(((x-((0--2)--1))**2)+0)
((-0.057+0)+((x-((0--2)--1))**2.000))
((-0.057+0)+((x-3)**2.000))
(((-0.057+0)**-1)+((x-3)**2.000))
(((-0.057+0)**-1)+((x-4)**2.000))
(((-0.057+0)**-1.000)+((x-4)**2.000))
(((-0.057+0.000)**-1.000)+((x-4)**2.000))
(((x-4)**2.000)+((-0.057+0.000)**-1.000))
(((x-4)**2)+((-0.057+0.000)**-1.000))
(((x-4)**2)+((-0.057+0.000)**-0.919))
((((x-4)**2)+((-0.057+0.000)**-0.919))+-0.048)
((((-0.057+0.000)**-0.919)+((x-4)**2))+-0.048)
((((-0.057+0.000)**-0.919)+((x-4)**2))+-0.037)
(((-0.057**-0.919)+((x-4)**2))+-0.037)
(-0.037+((-0.057**-0.919)+((x-4)**2)))
(-13.524+((x-4)**2))
(-13.500+((x-4)**2))
То есть после того как результаты вычислений окончательно стали совпадать с эталонными, он погнался за ресурсоемкостью, и провел преобразования, и в итоге формула на основе естественного отбора выигрывает по компактности!
Любопытно то, что такой результат я получил, фактически, по ошибке. При первых прогонах был запрещены виды мутации, при которых добавлялась бы еще одна переменная x. Как ни странно, так сработало даже лучше, чем при полноценной мутации. Вот результаты, когда баг был пофиксен:
- R = 250, X = 250, Y = 750, Точность = 0.001, (вес результата 49)
(2.500+((x-8)*x))
- R = 250, X = 1000, Y = 0, Точность = 0.001, (вес результата 60)
(((x-1)*(-7+x))-4.500)
В данном случае, вариант с квотой для случайных один раз споткнулся, но всё же смог выдать более оптимальный результат, чем второй вариант, который каждый из прогонов проходил ровно и однообразно. Здесь для каждого приближения результата к оптимуму хватает, в основном, одного шага мутации. В следующем случае всё окажется не так просто!
Второй эталон — натуральный логарифм:
ln (1 + x)
x принимает значения от 0 до 25.5, с шагом 0.1
Наши решения лишены возможности использовать логарифмы напрямую, но данный эталон раскладывается в ряд Тейлора:
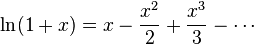
Вот и посмотрим, сможет ли решение воспроизвести такой ряд с заданной точностью.
Поначалу, пробовал прогоны с точностью до 0.001, но после нескольких суток упорной работы алгоритма решения достигли точности только около 0.0016, а размер выражений стремился к тысяче символов, и я решил снизить планку точности до 0.01. Результаты таковы:
- R = 250, X = 250, Y = 750, Точность = 0.01, (вес результата 149)
((((-1.776-x)/19.717)+(((x*x)-0.318)**0.238))-(0.066/(x+0.136)))
- R = 250, X = 1000, Y = 0, Точность = 0.01, (вес результата 174)
(((-0.025*x)+(((x*x)**0.106)**2))/(1+(0.849/((x*x)+1))))
Как видите, в случае включения случайных выживших для данного эталона найдено менее ресурсоемкое решение, с сохранением заданной точности. Не то, чтобы это сильно походило на ряд Тейлора, но оно считает верно :)
Третий эталон — синус, задаваемый в радианах:
sin (x)
x принимает значения от 0 до 6.28, с шагом 0.02
Опять же, эталон раскладывается в ряд Тейлора:
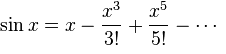
В данном случае, учитывая что при любом x результат принимает значение от -1 до 1, точность определения в 0.01 была более серьёзным испытанием, но алгоритм справился.
- R = 250, X = 250, Y = 750, Точность = 0.01, (вес результата 233)
((((-0.092**x)/2.395)+(((-1.179**((((x-1)*0.070)±0.016)*4.149))-(0.253**x))+0.184))**(0.944-(x/-87)))
- R = 250, X = 1000, Y = 0, Точность = 0.01, (вес результата 564)
(((x+x)*((x*-0.082)**(x+x)))+(((x+x)**(0.073**x))*((((1-(-0.133*x))*(-1-x))*((x/-1)*(-0.090**(x--0.184))))+(((((-1.120+(x*((x+1)*-0.016)))**(-0.046/((0.045+x)**-1.928)))+(-0.164-(0.172**x)))*1.357)**0.881))))
Опять же, ввиду повышенной сложности эталона, лучшего результата добилась версия алгоритма с пулом случайным решений.
Четвертый эталон — выражение с четырьмя (совпадение? не думаю) переменными:
2*v + 3*x — 4*y + 5*z — 6
Каждая из переменных принимает значения от 0 до 3 c шагом 1, всего 256 комбинаций.
- R = 250, X = 250, Y = 750, Точность = 0.01, (вес результата 254)
((y*0.155)+(-2.166+(((((z*4)-(((y-(x+(y/-0.931)))*2)±0.105))+((v+(v-2))±0.947))+x)+(z±1))))
- R = 250, X = 1000, Y = 0, Точность = 0.01, (вес результата 237)
((-3+(v+z))+(((v+((x-y)+((((z+z)-(((0.028-z)-x)+(y+y)))-y)+z)))+x)±2.963))
Вопреки моим ожиданиям, трудоемкость по сравнению с первым эталоном подскочила очень серьезно. Вроде бы эталон не сложный, можно спокойно шаг за шагом наращивать решение, приближая результат к нужному. Однако точность в 0.001 была так и не осилена! Тут я и начал подозревать, что проблемы с масштабированием задач у нашего подхода серьезные.
Итоги
В целом, я остался скорее не доволен полученными результатами, особенно, по эталонам 2 и 3. Понадобились тысячи поколений, чтобы вывести в итоге громоздкие формулы. Я вижу три варианта, почему это случается:
- Несовершенный механизм сокращения — например, не хватает более дальновидного раскрытия скобок\выноса за скобки. Из-за этого формулы не привести в удобный вид.
- Слишком спонтанная мутация, причем, чем больше формула, тем меньше вероятность правильного дальнейшего развития. Я подумывал о создании «исчерпывающего» (exhaustive) механизма мутации, когда формируется группа условно всех возможных мутантов на базе оригинала, и над ней производится пред-селекция. Дойдут ли руки проверить догадку, улучшит ли это алгоритм, пока неизвестно.
- Принципиальная непрактичность такого метода для нахождения решений сложных задач. Быть может, данный подход не так уж далеко ушел от попыток написать «Войну и мир» силами армии обезьян с пишущими машинками. Быть может, сложность, необходимость аналитического подхода, это природное и неотъемлемое свойство таких задач.
Курьёз
Вспомнил, как лет десять назад интересовался сжатием данных, пробовал силы в написании своего решения. Сокрушался, что никак не удается сжимать рандомные паттерны, пока меня не просветили :) Может, и здесь так?
Дальнейшие эксперименты
Здесь должен был идти рассказ про более амбициозный эксперимент, целью которого является автоматическая генерация алгоритма сортировки массива.
Был создан минимально допустимый набор выражений, состоящий из примитивов и управляющих структур (следований, циклов, ветвлений) позволяющий реализовать наивные сортировки (как минимум, «пузырьковую» и «выбором»), а также простейшая виртуальная машина, предназначенная исключительно для сортировки массивов.
Но рассказа здесь нет — эксперимент еще не проведен. Реализация мутирования еще далека от завершения. Плюс, итоги первого эксперимента заставили меня сильно усомниться в шансах на успех с сортировками: если в первом случае хоть как-то присутствует возможность линейного наращивания решения с планомерными приближением к эталонному результату, то в случае с сортировками, алгоритмы с единственным неверным шагом коверкают результат до неузнаваемости.
Как в таких условиях адекватно оценить, насколько хорошо претендент прошел испытание? У меня нет ответа. Как выбрать из двух претендентов, если они одинаково не отсортировали массив, но за разное количество выполненных команд? Выбрав простой, мы можем скатиться к доминированию претендентов типа
nil
Выбор более сложного контринтуитивен — зачем эволюции намеренное усложнение при одинаковой эффективности? Так что с селекцией тоже проблемы.
Возможно, к тому моменту, как будет дописана основная часть кода, я поменяю цели на более простые — например, на алгоритм нахождения индекса максимального элемента массива. Надеюсь, так у генетического алгоритма будет хоть какое-то ощутимое преимущество перед брутфорсным построением решения с перебором всех доступных комбинаций.
Если будет о каком успехе докладывать, будет и вторая часть статьи.
Закончим на этой задумчиво неопределенной ноте. Большое спасибо за уделенное время!
