Генераторы дискретно распределенных случайных величин
Данная статья является продолжением поста Генераторы непрерывно распределенных случайных величин. В этой главе учитывается, что все теоремы из предыдущей статьи уже доказаны и генераторы, указанные в ней, уже написаны. Как и ранее, у нас имеется некий базовый генератор натуральных чисел от 0 до RAND_MAX:
unsigned long long BasicRandGenerator() {
unsigned long long randomVariable;
// some magic here
...
return randomVariable;
}
С дискретными величинами все интуитивно понятнее. Функция распределения дискретной случайной величины:
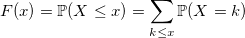
Несмотря на простоту распределений дискретных случайных величин, генерировать их подчас сложнее, нежели чем непрерывные. Начнем, как и в прошлый раз, с тривиального примера.
Распределение Бернулли
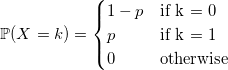
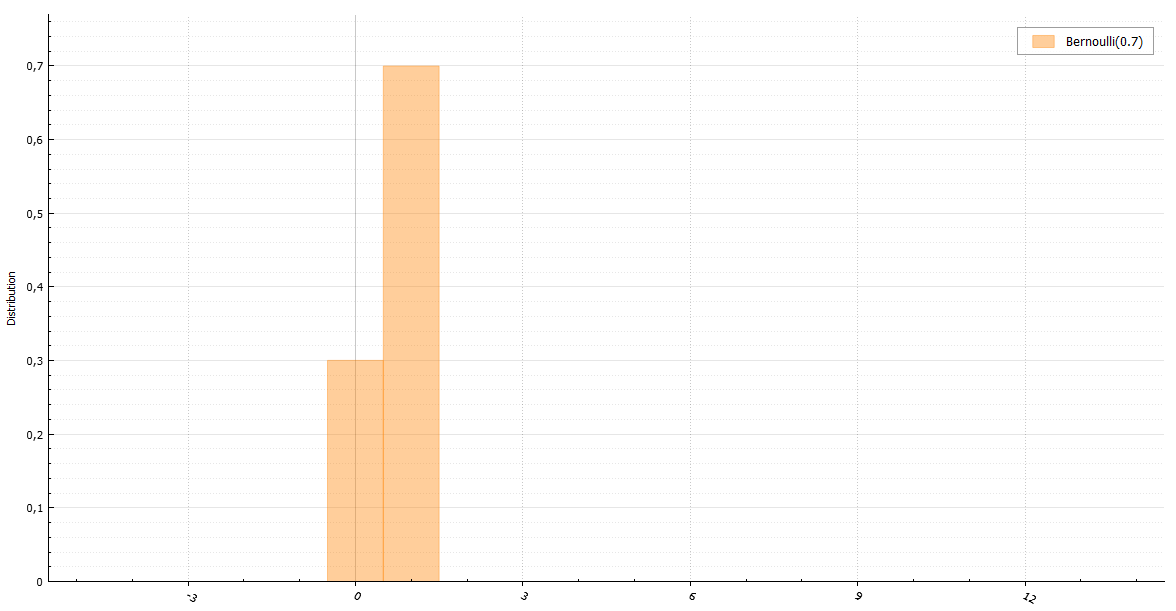
Пожалуй, самый быстрый из очевидных способов сгенерировать случайную величину с распределением Бернулли — это сделать подобным образом (все генераторы возвращают double лишь для единства интерфейса):
void setup(double p) {
unsigned long long boundary = (1 - p) * RAND_MAX; // we storage this value for large sampling
}
double Bernoulli(double) {
return BasicRandGenerator() > boundary;
}
Иногда можно сделать быстрее. «Иногда» означает «в случае, при котором параметр p является степенью ½». Дело в том, что если целое число, возвращаемое функцией BasicRandGenerator () является равномерно распределенной случайной величиной, то равномерно распределен и каждый его бит. А это значит, что в двоичном представлении число состоит из битов, распределенных по Бернулли. Так как в данных статьях функция базового генератора возвращает unsigned long long, то мы имеем 64 бита. Вот какой трюк можно провернуть для p = ½:
double Bernoulli(double) {
static const char maxDecimals = 64;
static char decimals = 1;
static unsigned long long X = 0;
if (decimals == 1)
{
/// refresh
decimals = maxDecimals;
X = BasicRandGenerator();
}
else
{
--decimals;
X >>= 1;
}
return X & 1;
}
Если же время работы функции BasicRandGenerator () недостаточно мало, а криптоустойчивостью и размером периода генератора можно пренебречь, то для таких случаев существует алгоритм, использующий лишь одну равномерно распределенную случайную величину для любого размера выборки из распределения Бернулли:
void setup(double p) {
q = 1.0 - p;
U = Uniform(0, 1);
}
double Bernoulli(double p) {
if (U > q)
{
U -= q;
U /= p;
return 1.0;
}
U /= q;
return 0.0;
}
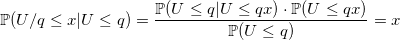
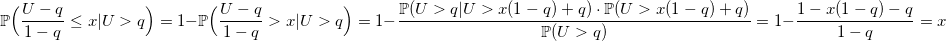
Равномерное распределение
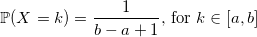
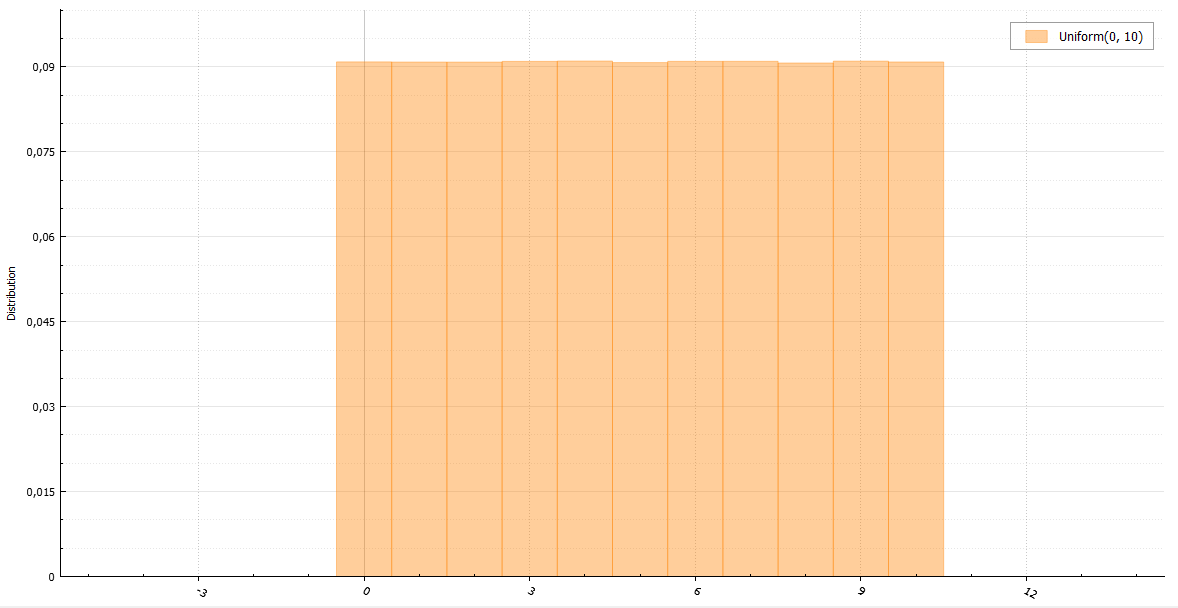
Уверен, что любой из вас вспомнит, что его первый генератор случайного целого числа от a до b выглядел похожим на это:
double UniformDiscrete(int a, int b) {
return a + rand() % (b - a + 1);
}
Что ж, и это вполне правильное решение. С единственным и не всегда верным предположением — у вас хороший базовый генератор. Если же он дефективный как старый С-шный rand (), то вы будете получать четное число за нечетным каждый раз. Если вы не доверяете своему генератору, то лучше пишите так:
double UniformDiscrete(int a, int b) {
return a + round(BasicRandGenerator() * (b - a) / RAND_MAX);
}
Еще следует заметить, что распределение не будет совсем равномерным, если RAND_MAX не делится длину интервала b — a + 1 нацело. Однако, разница будет не столь значима, если эта длина достаточно мала.
Геометрическое распределение


Случайная величина с геометрическим распределением с параметром p — это случайная величина с экспоненциальным распределением с параметром -ln (1 — p), округленная вниз до ближайшего целого.
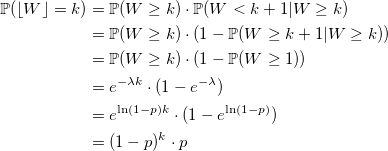
void setupRate(double p) {
rate = -ln(1 - p);
}
double Geometric(double) {
return floor(Exponential(rate));
}
Можно ли сделать быстрее? Иногда. Посмотрим на функцию распределения:
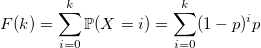
и воспользуемся обыкновенным методом инверсии: генерируем стандартную равномерно распределенную случайную величину U и возвращаем минимальное значение k, для которого эта сумма больше U:
double GeometricExponential(double p) {
int k = 0;
double sum = p, prod = p, q = 1 - p;
double U = Uniform(0, 1);
while (U < sum) {
prod *= q;
sum += prod;
++k;
}
return k;
}
Такой последовательный поиск довольно эффективен, учитывая, что значения случайной величины с геометрическим распределением сконцентрированы возле нуля. Алгоритм, однако, быстро теряет свою скорость при слишком маленьких значениях p, и в таком случае лучше все же воспользоваться экспоненциальным генератором.
Есть секрет. Значения p, (1-p) * p, (1-p)^2 * p, … можно посчитать заранее и запомнить. Вопрос в том, где остановиться. И тут на сцену выходит свойство геометрического распределения, которое оно унаследовало от экспоненциального — отсутствие памяти:
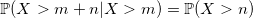
Благодаря такому свойству, можно запомнить лишь несколько первых значений (1-p)^i * p и затем воспользоваться рекурсией:
// works nice for p > 0.2 and tableSize = 16
void setupTable(double p) {
table[0] = p;
double prod = p, q = 1 - p;
for (int i = 1; i < tableSize; ++i)
{
prod *= q;
table[i] = table[i - 1] + prod;
}
}
double GeometricTable(double p) {
double U = Uniform(0, 1);
/// handle tail by recursion
if (U > table[tableSize - 1])
return tableSize + GeometricTable(p);
/// handle the main body
int x = 0;
while (U > table[x])
++x;
return x;
}
Биномиальное распределение

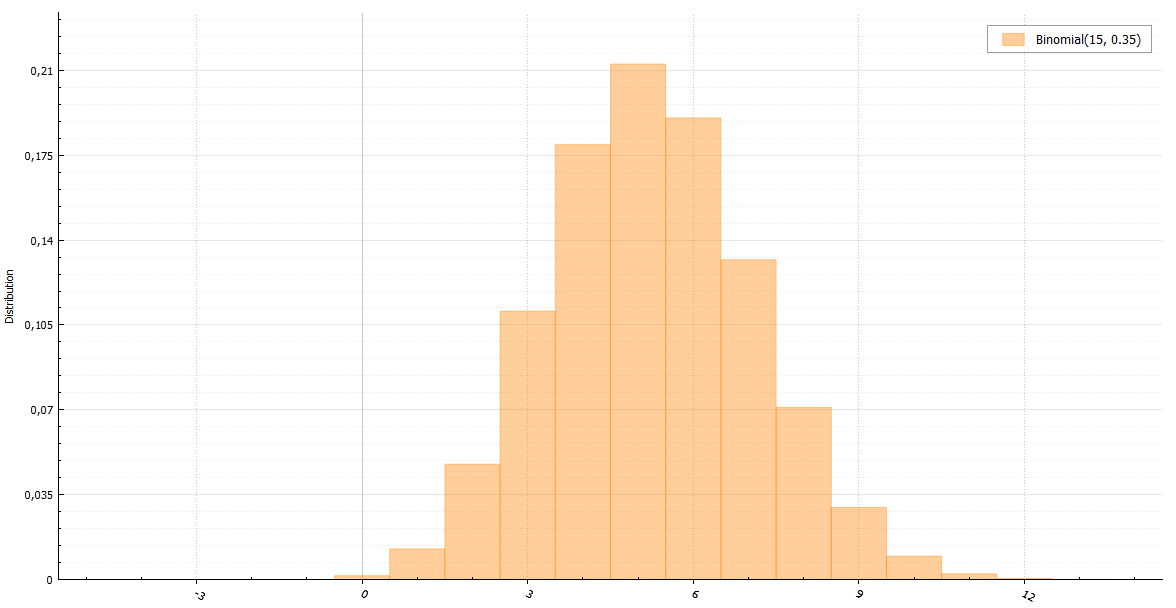
По определению случайная величина с биномиальным распределением — это сумма n случайных величин с распределением Бернулли:
double BinomialBernoulli(double p, int n) {
double sum = 0;
for (int i = 0; i != n; ++i)
sum += Bernoulli(p);
return sum;
}
Однако, есть линейная зависимость от n, которую нужно обойти. Можно воспользоваться теоремой: если Y_1, Y_2, … — случайные величины с геометрическим распределением с параметром p и X — наименьшее целое, такое что:
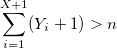
то X имеет биномиальное распределение.

q.e.d.
Время работы следующего кода растет только с увеличением величины n * p.
double BinomialGeometric(double p, int n) {
double X = -1, sum = 0;
do {
sum += Geometric(p) + 1.0;
++X;
} while (sum <= n);
return X;
}
И все же, временная сложность растет.
У биномиального распределения есть одна особенность. При росте n оно стремится к нормальному распределению или же, если p ~ 1/n, то к распределению Пуассона. Имея генераторы для этих распределений, можно ими заменить генератор для биномиального в подобных случаях. Но что, если этого недостаточно? В книге Luc Devroye «Non-Uniform Random Variate Generation» есть пример алгоритма, работающего одинаково быстро для любых больших значений n * p. Идея алгоритма состоит в выборке с отклонением, используя нормальное и экспоненциальное распределения. К сожалению, рассказ о работе этого алгоритма будет слишком большим для данной статьи, но в указанной книге он исчерпывающе описан.
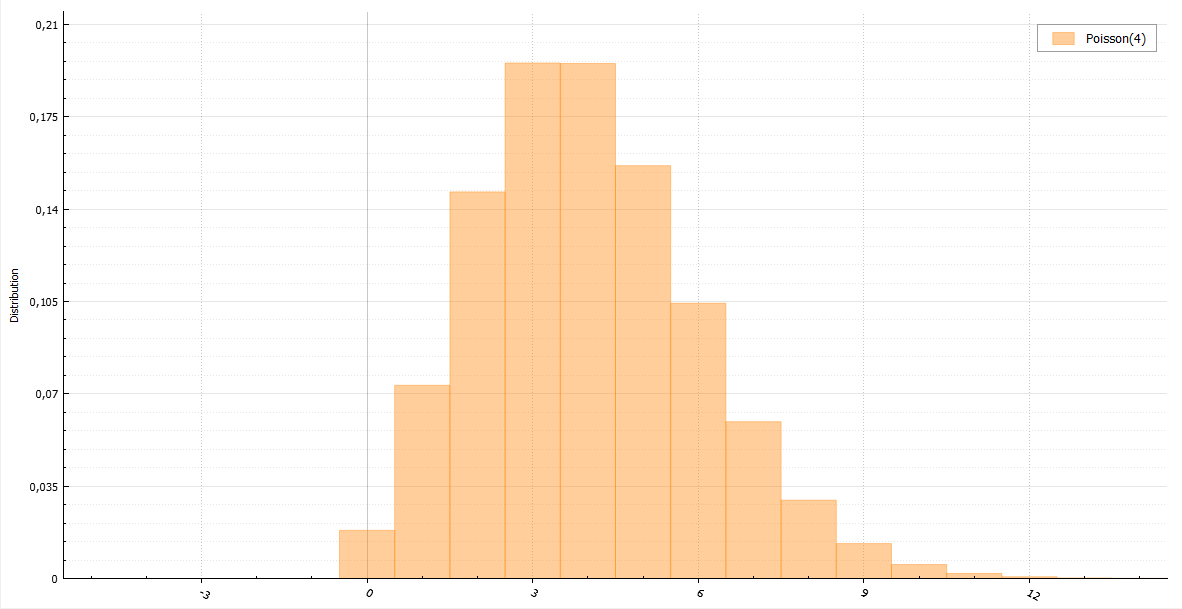
Распределение Пуассона
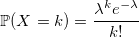
Если W_i — случайная величина со стандартным экспоненциальным распределением с плотностью lambda, то:
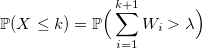
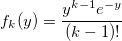
тогда
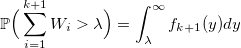
и вероятность получить k:
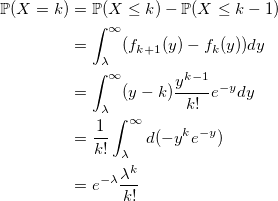
совпадает с распределением Пуассона. q.e.d.
Используя это свойство, можно написать генератор через сумму экспоненциально распределенных величин с плотностью rate:
double PoissonExponential(double rate) {
int k = -1;
double s = 0;
do {
s += Exponential(1);
++k;
} while (s < rate);
return k;
}
На этом же свойстве основан популярный алгоритм Кнута. Вместо суммы экспоненциальных величин, каждую из которых можно получить методом инверсии через -ln (U), используется произведение равномерных случайных величин:

и тогда:

Запомнив заранее значение exp (-rate), последовательно перемножаем U_i, пока произведение его не превысит.
void setup(double rate)
expRateInv = exp(-rate);
}
double PoissonKnuth(double) {
double k = 0, prod = Uniform(0, 1);
while (prod > expRateInv) {
prod *= Uniform(0, 1);
++k;
}
return k;
}
Можно же использовать генерацию только лишь одной случайной величины и метод инверсии:

Поиск k, удовлетворяющего такому условию лучше начинать с наиболее вероятного значения, то есть с floor (rate). Сравниваем U с вероятностью, что X
void setup(double rate)
floorLambda = floor(rate);
FFloorLambda = F(floorLamda); // P(X < floorLambda)
PFloorLambda = P(floorLambda); // P(X = floorLambda)
}
double PoissonInversion(double) {
double U = Uniform(0,1);
int k = floorLambda;
double s = FFloorLambda, p = PFloorLambda;
if (s < U) {
do {
++k;
p *= lambda / k;
s += p;
} while (s < U);
}
else {
s -= p;
while (s > U) {
p /= lambda / k;
--k;
s -= p;
}
}
return k;
}
Проблема всех трех генераторов в одном — их сложность растет вместе с параметром плотности. Но есть спасение — при больших значениях плотности распределение Пуассона стремится к нормальному распределению. Можно также использовать непростой алгоритм из вышеуказанной книги «Non-Uniform Random Variate Generation», ну, или же, попросту аппроксимировать, пренебрегая точностью во имя скорости (смотря какая стоит задача).
Отрицательное биномиальное распределение
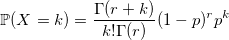
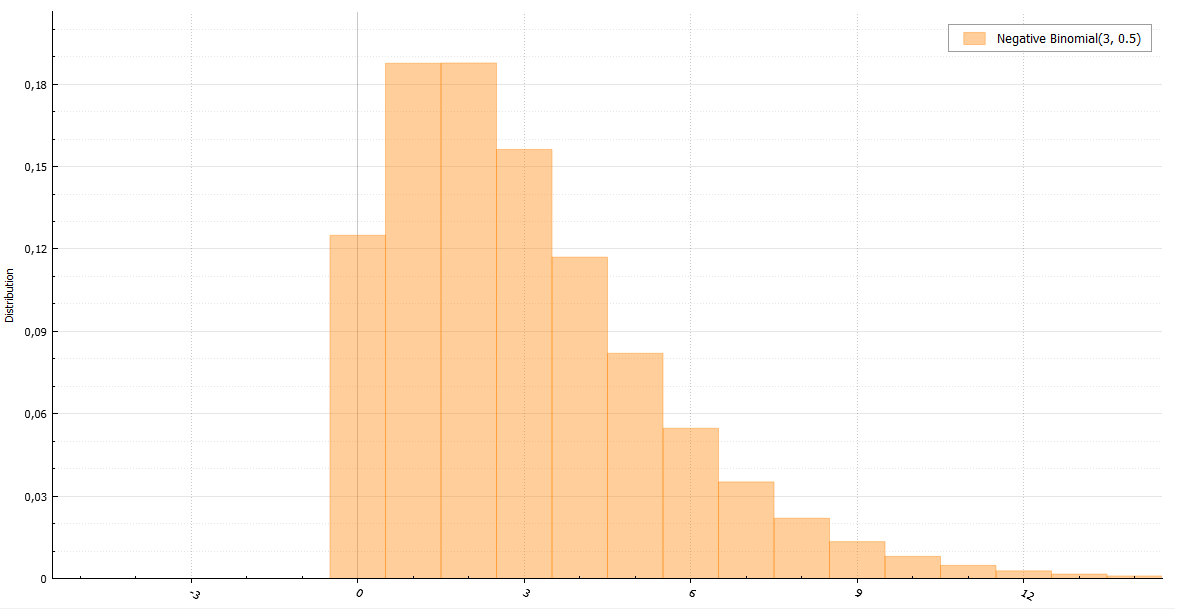
Отрицательное биномиальное распределение еще именуется распределением Паскаля (если r целое) и распределением Поля (если r может быть вещественным). Используя характеристическую функцию, легко доказать, что распределение Паскаля — это сумма r геометрически распределенных величин с параметром 1 — p:
double Pascal(double p, int r) {
double x = 0;
for (int i = 0; i != r; ++i)
x += Geometric(1 - p);
return x;
}
Проблема такого алгоритма налицо — линейная зависимость от r. Нам нужно что-то такое, что будет работать одинаково хорошо при любом параметре. И в этом нам поможет отличное свойство. Если случайная величина X имеет распределение Пуассона:

где плотность случайна и имеет гамма-распределение:
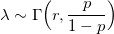
то X имеет отрицательное биномиальное распределение. Поэтому, оно иногда называется гамма-распределением Пуассона.
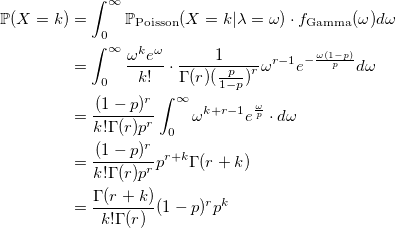
Теперь, мы можем быстро написать генератор случайной величины с распределением Паскаля для больших значений параметра r.
double Pascal(double p, int r) {
return Poisson(Gamma(r, p / (1 - p)));
}
Гипергеометрическое распределение
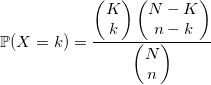
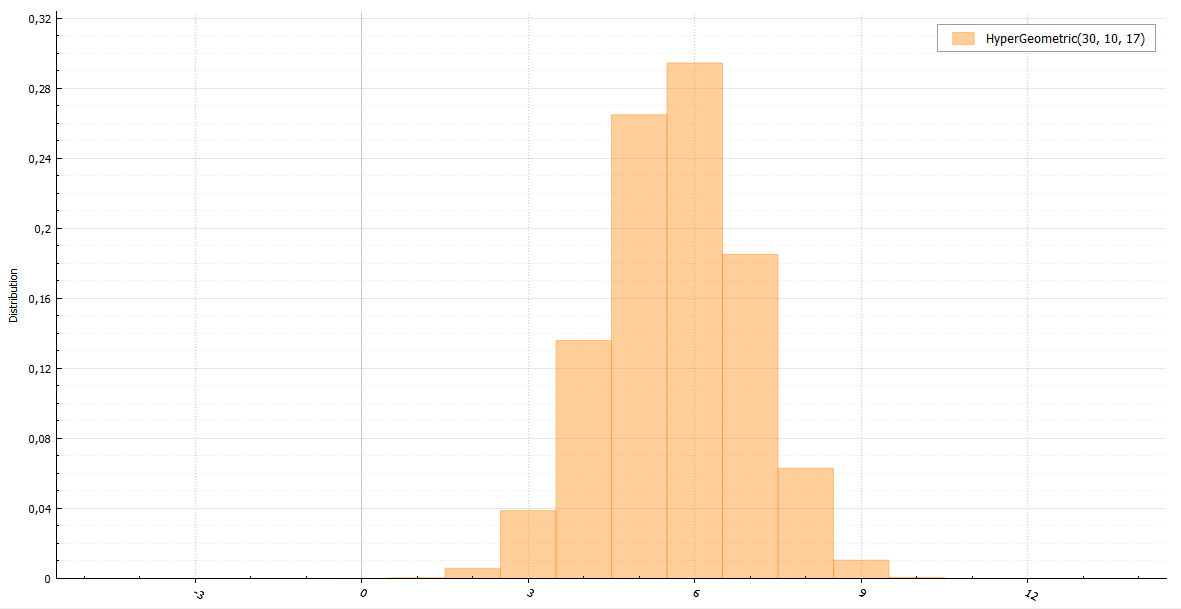
Представьте, что в урне находится N шаров и K из них белые. Вы вытаскиваете n шаров. Количество белых среди них будет иметь гипергеометрическое распределение. В общем случае лучше брать алгоритм, использующий это определение:
double HyperGeometric(int N, int n, int K) {
int sum = 0;
double realK = static_cast(K);
double p = realK / N;
for (int i = 1; i <= n; ++i)
{
if (Bernoulli(p) && ++sum == K)
return sum;
p = (realK - sum) / (N - i);
}
return sum;
}
Или же можно воспользоваться выборкой с отклонением через биномиальное распределение с параметрами:
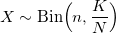
и константой М:
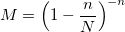
Алгоритм с биномиальным распределением хорошо работает в экстремальных случаях при больших n и еще больших N (таких, что n
Логарифмическое распределение

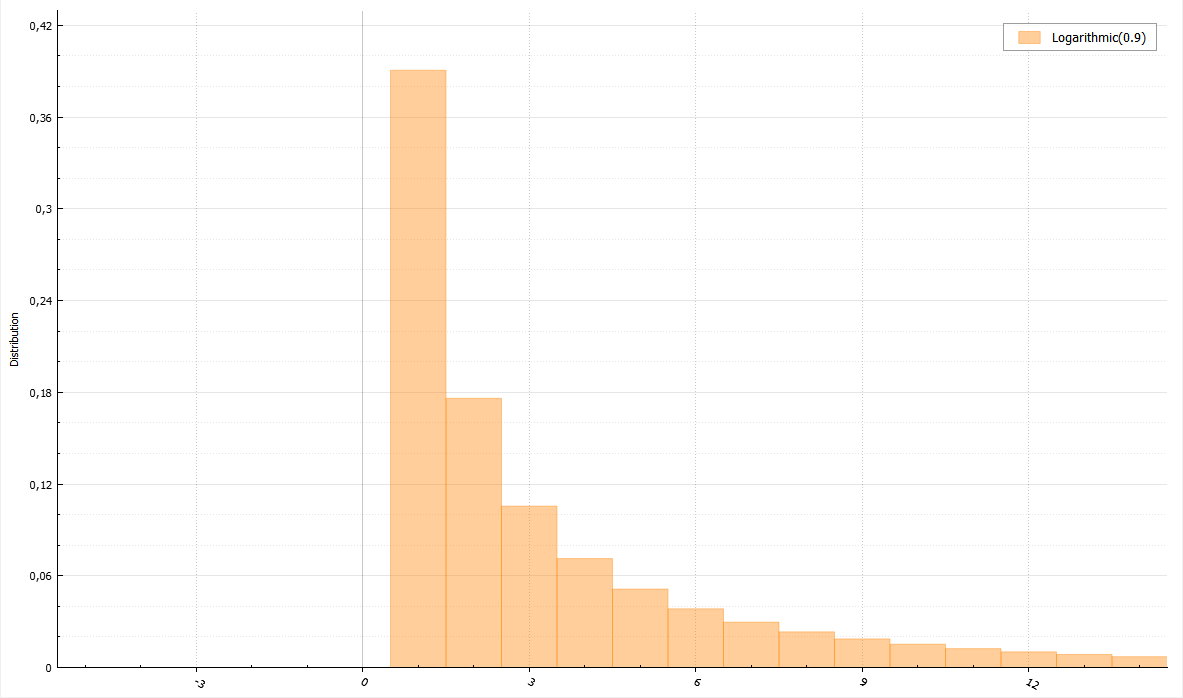
Для данного распределения существует полезная теорема. Если U и V — равномерно распределенные случайные величины от 0 до 1, то величина
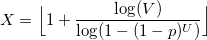
будет иметь логарифмическое распределение.
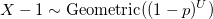
Докажем, что X имеет логарифмическое распределение:
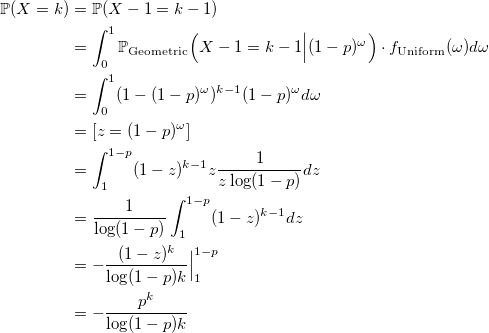
q.e.d.
Для ускорения алгоритма можно воспользоваться двумя уловками. Первая: если V > p, то X = 1, т.к. p >= 1-(1-p)^U. Вторая: пускай q = 1-(1-p)^U, тогда если V > q, то X = 1, если V > q^2, то X = 2 и т.д. Таким образом, можно возвращать наиболее вероятные значения 1 и 2 без частых подсчетов логарифмов.
void setup(double p) {
logQInv = 1.0 / log(1.0 - p);
}
double Logarithmic(double p) {
double V = Uniform(0, 1);
if (V >= p)
return 1.0;
double U = Uniform(0, 1);
double y = 1.0 - exp(U / logQInv);
if (V > y)
return 1.0;
if (V <= y * y)
return floor(1.0 + log(V) / log(y));
return 2.0;
}
Зета распределение
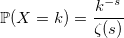
В знаменателе — зета-функция Римана:
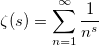
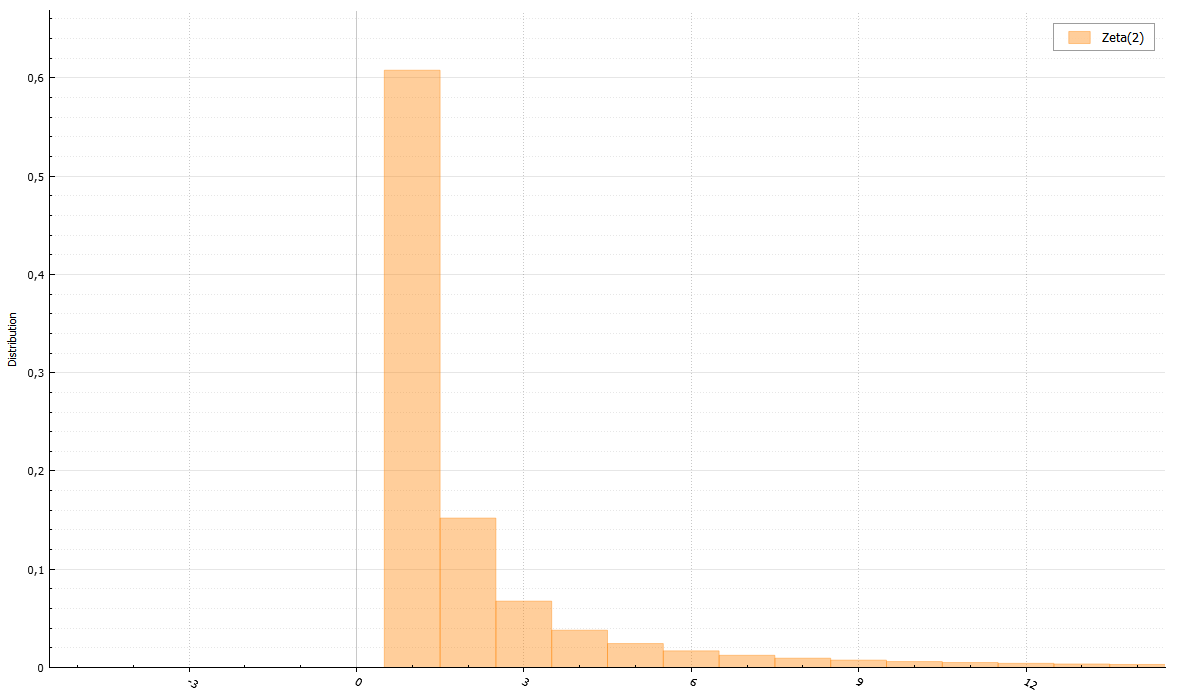
Для зета распределения существует алгоритм, позволяющий не вычислять римановскую зета-функцию. Нужно лишь уметь генерировать распределение Парето. Доказательство могу приложить по просьбе читателей.
void setup(double s) {
double sm1 = s - 1.0;
b = 1 - pow(2.0, -sm1);
}
double Zeta(double) {
/// rejection sampling from rounded down Pareto distribution
int iter = 0;
do {
double X = floor(Pareto(sm1, 1.0));
double T = pow(1.0 + 1.0 / X, sm1);
double V = Uniform(0, 1);
if (V * X * (T - 1) <= T * b)
return X;
} while (++iter < 1e9);
return NAN; /// doesn't work
}
Напоследок маленькие алгоритмы для прочих сложных распределений:
double Skellam(double m1, double m2) {
return Poisson(m1) - Poisson(m2);
}
double Planck(double a, double b) {
double G = Gamma(a + 1, 1);
double Z = Zeta(a + 1)
return G / (b * Z);
}
double Yule(double ro) {
double prob = 1.0 / Pareto(ro, 1.0);
return Geometric(prob) + 1;
}
