Гедоммист и ближайшие соседи23.11.2016 22:34

dfad2b4dbb794a73a70f5e2d3c336fcb.png

Гедоммист (в Древнем Риме) — человек, получающий кайф от программирования.

Увлечению программированием сопутствуют опасности — антисанитария, забытые дети, служебные выговоры, сбежавшее молоко или летящий в висок женский сапог.

Помню об этом, одолевая манящие сложностью алгоритмы.

И хочу рассказать об одной бесполезной задаче, которую я решал неделю в полном экстазе. Задача родилась благодаря 3aicheg, чей комментарий дал мне идею для игры под iOS (вижу Ваши глаза, Шо опять?). Смысл в том, чтобы сделать match game на нерегулярной сетке с гравитацией.

Кстати, если вы думаете, что рассказывая здесь о своем бесплатном приложении, можно получить мировую славу и купить яхту, то вот таблица

Рейтинг статьи Просмотров статьи Просмотров видео Загрузок
+30 20 000 5 000 18
-2 2 500 2 000 14

И потому я восхищаюсь бескорыстными авторами Хабра (особенно теми, кто владеет русским слогом). Теперь к делу! А дело такое…

Постановка задачи
Задача основна на множестве точек, случайным образом наброшенных в заданный прямоугольник. Для каждой точки находятся ближайшие соседи (строится диаграмма Вороного), точки раскрашиваются в случайные цвета радуги. Затем начинается игра — по нажатию удаляются цветные цепочки и под действием силы тяжести в образованные пустоты проваливаются/затекают оставшиеся ячейки. Конфигурация сетки при этом уже не меняется.

Задачка 1 — расстановка начальных данных


Итак, рассмотрим прямоугольник (экран нашего телефона), вершины прямоугольника перенумерованы 0, 1, 2, 3. Внутри этого прямоугольника будут твориться всякие безобразия.
330255021fdd435ba5150710c30954ba.png

Рис. 1 Прямоугольник с вершинами 0, 1, 2, 3

Бросим в данный прямоугольник случайно N точек, пронумеруем их от 4 до 4+N. Почему от 4? Потому что все места (0–3) уже заняты бегемотиками.

2c57bb094573411ba595ce64b213a089.png

Рис. 2 Набор случайных точек

Случайный разброс порой опасен — некоторые точки могут упасть слишком близко друг от друга, так что игрок не сможет различать их на экране и нажать на приглянувшуюся ему точку. Зная физический размер отпечатка указательного пальца игрока, я добавляю условие, что расстояние между точками должно быть не менее 26 пикселов. Каким образом удовлетворить этому условию? Два способа 1) Двигать точки в направлении разреженного пространства и 2) бросать новую точку, пока не выполнится условие radiusMin>26. Второй способ легче, но опасней — возможно зацикливание при слишком больших значениях N. Но у меня с N все в порядке, запас свободной площади пятикратный и потому двигаемся дальше, а именно находим ближайших соседей для всех наших точек. Идем по порядку, то есть сначала ищем соседей для точки с номером, как вы понимаете, 4.

Для этого упорядочим по часовой стрелке все радиус-векторы от нашей точки до всех остальных.

942ab49db5a84277b194c3822cc1c404.png

Рис. 3 Упорядочим радиус-векторы [9–7–5–10–11–8–6]

На языке Swift это выглядит так: 

                let x0 = pts[4].x
                let y0 = pts[4].y
                var vtx = [Point]()
                for i in 5.. $1.angle })

Теперь в нашем массиве vtx хранятся вершины [9–7–5–10–11–8–6], пройдемся по ним и построим многоугольник, окружающий искомую точку с номером 4. Итак, изначально, нашу точку окружает прямоугольник с вершинами [0–1–2–3], как на рис. 1.

Берем первую вершину из упорядоченного списка — это точка с номером 9. Строим перпендикуляр к отрезку [4–9], делящий его пополам.

68fdeed9c3914f03816b0158a960de20.png

Рис. 4 Прямая, равноудаленая от точек 4 и 9

Получившаяся прямая либо пересекает многоугольник [0–1–2–3], либо нет. Глядя на рисунок 4 легко обнаружить, что пересекает. Уравнение пересечения отрезка и прямой я решил не приводить. Таким образом вместо [0–1–2–3] получился многоугольник [0–1–9–3], который мы видим на рисунке 5.

8d8eb7fb18324d8f9d645d6aed01cf0f.png

Рис. 5 Многоугольник [0–1–9–3]

Переходим к следующей точке из списка [9–7–5–10–11–8–6]. Это точка номер 7. Делаем все то же самое — строим перпендикуляр, равноудаленный от точек 4 и 7 и проверяем, пересекает он наш многоугольник [0–1–9–3].

71d10f7d4ff045c492bdd472a77f1d2e.png

Рис. 6 Многоугольник [0–1–9–3] не пересекается прямой [4–7]

Не пересекает, делать ничего не надо, следовательно переходим к следующей паре точек с номерами 4 и 5.

3077a5052e25424e8c3d1f0dd78557f5.png1256d8e117b643c2abe92096dbcf5608.png
Рис. 7 Многоугольник [0–1–9–5–3]

И так далее. Метод Форчуна (так любимый на Хабре, уже 3 статьи про него листал) для ускорения нахождения соседей применять здесь не стоит, поскольку нет у нас 100 000 точек в задаче. И 1000 точек нет. А сколько? 50–70 точек — это число обусловлено физическим размером экрана телефона. Вот финальная картина для многоугольника вокруг первой вершины с номером 4

d08b93792d124aea88df1c66e1fae467.pngd507faa13ead44d7bba7206f399a0d44.png
Рис. 8 Многоугольник [0–6–9–10–8–3]

Для рисования многоугольников я использую родной UIKit с заливкой текстурой (оттуда же и рисование линий). Пример кода внутри func draw (_ rect: CGRect): 

    let colors:[UIColor] = [UIColor.black,
       UIColor(patternImage: UIImage(named: "b_19.png")!),
       UIColor(patternImage: UIImage(named: "b_20.png")!),
       UIColor(patternImage: UIImage(named: "b_21.png")!),
       UIColor(patternImage: UIImage(named: "b_22.png")!),
       UIColor(patternImage: UIImage(named: "b_23.png")!),
    ]
 
    func renderSimple(_ t:Convex)
    {
        let path = UIBezierPath()
        let strokeColor = UIColor.black
        strokeColor.setStroke()
        path.lineWidth = 1.0
        let clr = t.color
        var i = 0
        for p in t.vtx {
            if i == 0 {
                i = 1
                path.move(to: p)
            } else {
                path.addLine(to: p)
            }
        }
        if clr>0 {
            let fillColor = colors[clr]
            fillColor.setFill()
            path.fill()
        }
        path.stroke()
    }

Ух. Устал сочинять. Разомнем пальчики сыграем пару уровней в получившейся игре Zabivaka
fdf6f76c9ad24a288a88d69db1f42c3d.png

Идем дальше. Получилась такая случайная, но симпатичная картина.

2b967ffdee6b46db899634643dcd9aef.pnga38b082f17db4d9ab35654a106622f7c.png

a6f43f88ea3443f3bc365be6c64d9e81.pnga6f43f88ea3443f3bc365be6c64d9e81.png
Рис. 9 Уровень Канзас — так и хочется нажать и очистить синюю цепочку

Если у вас возникло такое желание (нажать и очистить синюю цепочку) — значит, игра не самая плохая. Как видно, нужно было придумать закон по перетеканию цветных ячеек в освобождающиеся пустые клетки. Почему они должны перетекать или сдвигаться? Потому что в игре включено поле силы тяжести. После численных экспериментов я набрел на закон Трампа-Галилея — частица перемещается в пустую соседнюю, если центр тяжести последней находится ниже центра тяжести исходной частицы. Желе вверх не течет. И второе условие — низшая точка общей границы двух частиц должна быть ниже центра тяжести исходной частицы — это значит, что желе не течет через высокий край стакана. В игровом процессе данный закон был мной незамедлительно опробован и одобрен.

Единственное, что понадобилось запрограммировать для данного закона — это алгоритм вычисления центра тяжести произвольного многоугольника. Вначале я думал, что это просто — как в треугольнике — найти среднее арифметическое координат вершин! Лошара, скажете Вы и будете правы. Разбил многоугольник на треугольники, просуммировал центры тяжести треугольников пропорционально их размерам (площадям). Все стало красиво. Если будут от вас отзывы об игре — пишите, я сейчас живу одиноко — буду рад любому комментарию.

Меню


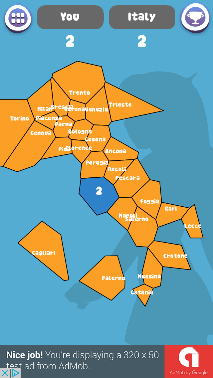
В любой игре необходима цель — обычно ты должен пройти все уровни. Уровни изображают по всякому — например, это города на карте, которые ты должен покорить. Я решил, что триангуляция — отличный способ рисовать реальные карты (схематично, анимашно) не прикладывая никаких усилий. И действительно, я загрузил список городов мира с гео-координатами и построил на этих данных сетку по описанному выше алгоритму. И вот что получилось.

ce217d818b6842daa6822f1e2f841402.pngdcc08cc0b3ec498d97d73cc5f2337937.png

1183156d338744168ec30303d8c92444.png396cc656092944ff9021a6e1a3db63b4.png
Рис. 10 Карты узнаваемых стран

Список гео-координат для, например, Италии выглядит так: 

      City(name:"Rome",x:41.9000,y:12.4833,s:4),
        City(name:"Ancona",x:43.6333,y:13.5000,s:4),
        City(name:"Ascoli",x:42.8500,y:13.5667,s:4),
        City(name:"Bari",x:41.1333,y:16.8500,s:4),
        City(name:"Bologna",x:44.4833,y:11.3333,s:4),
        City(name:"Brescia",x:45.5500,y:10.2500,s:4),
        City(name:"Catania",x:37.5000,y:15.1000,s:4),
        City(name:"Cesena",x:44.1433,y:12.2497,s:4),
        City(name:"Cagliari",x:39.2167,y:9.1167,s:4),
        City(name:"Florence",x:43.7667,y:11.2500,s:4),

По-моему, отличный способ построения игровых карт. Разумеется, надо добавить паразитные точки, эмулирующие море или соседние страны. Я добавлял по 16 точек на каждую карту, некоторые паразитные точки приходилось редактировать ручками.

Для устрашения игрока я ввел правило — не более 15 кликов на партию. Было сложно тестировать игру в подобных условиях, я малодушно увеличил это число до 16. Кроме того, обнаружил ошибку на последнем ходе, но исправлять её не стал — эта ошибка помогает преодолеть казалось бы невозможные расклады. И придает настроения игре. Для великолепного мастерского прохождения уровня добавил бонусов — анимация грудастой девушки и пиратскую музыку. Короче, я лично доволен. Ну и вам, надеюсь, нескучно было почитать в эту ненастную пору историю про игрушку на Swifte.

Увидимся, братья…

Комментарии (1)

  • 23 ноября 2016 в 19:50

    +1

    ↑

    ↓

    Забыл ссылку — приложение бесплатное.
    Забивака

© Habrahabr.ru