Frogger HD и численное моделирование волн в пруду
После прочтения статьи про CGA от SLY_G я необычайно возбудился. Вспомнил юность, IBM PC/XT и игру frogger jr, в которой лягушка должна была пересечь дорогу, избежав колес бешено мчавшихся байков. Затем по бревнам допрыгать до тихой заводи. И так до смерти, которых выдавали 4 штуки. Фраю выдали 666, но я не Макс.Поплакав о безвозвратно потерянных годах, я решил потерять еще пару дней и сделал ремейк игры под iPad.
Движение воды в речке решил смоделировать по-правильному, через разностную схему.О численном алгоритме моделирования озерных волн и о том, что получилось, читайте дальше.Да! забыл сказать.Тем, кто может продолжить последовательность
T T F S E…
читать будет не особенно интересно.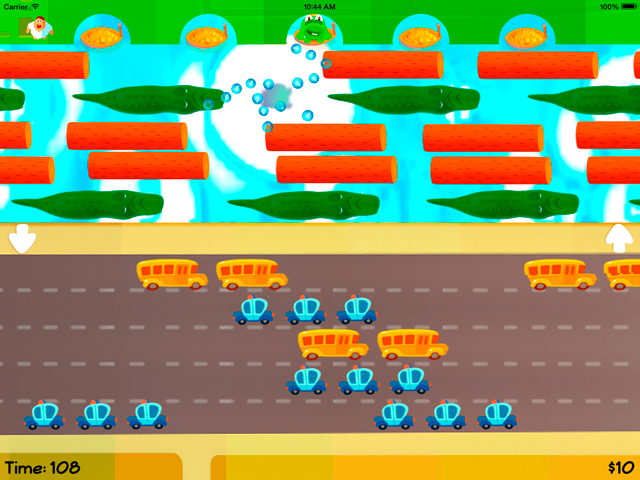
Итак, вода. Численно решить уравнения Навье-Стокса на телефона еще рано. Поэтому я взял модель, любезно увиденную в статье уважаемого господина blind_designer. В работе слепого Пью описан одномерный алгоритм. Я его расширил до двухмерного.
Модель поверхности воды.Представим прямоугольную сетку размером M*N. Сетка лежит на земле, из каждого узла торчит по пружине начальной длиной Lx0[i, j]. Упругость пружины определяется её коэффициентом kx[i, j].Набросим легкое покрывало на пружинки — это покрывало и будет моделировать зеркало водоема.
Под действием внешних сил (камень упал), длины пружинок Lx[i, j] могут измениться. Как мы помним из жизни, волны от брошенного камня рано или поздно успокаиваются.
Поэтому, заведем еще один массив вязкости пружины mx[i, j]. Если вязкость пружины положить равной 0, то волны никогда не остановятся и будут бесконечно долго отражаться от берегов.
Численное уравнение для пружинок совсем простое (закон Гука с диссипацией)
for (int i=0; i Если оставить решение в таком виде, то каждая пружинка будет раскачиваться сама по себе, не зависимо от соседних пружинок. В жизни не так, между соседями есть связь. Эту связь опишем через уравнение диффузии или (для дизайнеров) через фильтр шириной 9 пружинок. Фильтр размазывает скорость каждой пружины по 4 соседям в каждую сторону света, что и создает эффект волны. Следите за циклом
float spread = 0.025;
// do some passes where springs pull on their neighbours
for (int iki = 0; iki < 4; iki++) { // 4 соседа в каждую сторону должны почувствовать градиент
// размазываем по оси х
for (int j = 0; j < ny; j++) {
for (int k = 1; k < nx-1; k++) {
int i = k + j*nx;
lp[i] = spread * (Lx[i] - Lx[i-1]);
Wx[i - 1] += lp[i];
rp[i] = spread * (Lx[i] - Lx[i + 1]);
Wx[i + 1] += rp[i];
}
}
for (int j = 0; j < ny; j++) {
for (int k = 1; k < nx-1; k++) {
int i = k + j*nx;
Lx[i - 1] += lp[i];
Lx[i + 1] += rp[i];
}
}
// размазываем по оси y
for (int j = 1; j < ny-1; j++) {
for (int k = 0; k < nx; k++) {
int i = k + j*nx;
lp[i] = spread * (Lx[i] - Lx[i-nx]);
Wx[i - nx] += lp[i];
rp[i] = spread * (Lx[i] - Lx[i + nx]);
Wx[i + nx] += rp[i];
}
}
for (int j = 1; j < ny-1; j++) {
for (int k = 0; k < nx; k++) {
int i = k + j*nx;
Lx[i - nx] += lp[i];
Lx[i + nx] += rp[i];
}
}
}
Массивы lp[] и rp[] — временные, алгоритм сами оптимизируете под свои способности.nx — число узлов вдоль оси x, ny — число узлов вдоль оси y. Все ясно? По-моему, вполне, идем дальше, к визуализации. Визуализация
Вы можете нарисовать трехмерную поверхность. А я давно ушел от реализма OpenGL и покажу волны на плоской картинке. Как бы вид с вертолета, зависшего над озером. Пикассо сделал бы так же. Берём текстуру, со сторонами пропорциональными нашей сетке.Неплохо, если она будет похожа по цветоощущениям на воду в бассейне. Пример текстуры. Пижженно у зептолабов. Текстуру превращаем в двумерный массив rawData пикселов, каждый пиксел — 4 байта или RGBA компонентами.
myUIImage = [UIImage imageNamed:@«ground_2»];
n = nx*ny;
CGImageRef image = [myUIImage CGImage];
NSUInteger width2 = CGImageGetWidth (image);
NSUInteger height2 = CGImageGetHeight (image);
CGColorSpaceRef colorSpace = CGColorSpaceCreateDeviceRGB ();
bytesPerPixel2 = 4;
bytesPerRow2 = bytesPerPixel2 * width2;
NSUInteger bitsPerComponent = 8;
rawData = malloc (height2 * width2×4);
CGContextRef context = CGBitmapContextCreate (rawData, width2, height2, bitsPerComponent, bytesPerRow2, colorSpace, kCGImageAlphaPremultipliedLast | kCGBitmapByteOrder32Big);
CGColorSpaceRelease (colorSpace);
CGContextDrawImage (context, CGRectMake (0, 0, width2, height2), image);
CGContextRelease (context);
У нас все готово для моделирования.Есть начальная картинка — rawData[i, j].Есть текущая высота поверхности воды в каждой точке — Lx[i, j].Есть вертикальная скорость поверхности воды в каждой точке — Wx[i, j]. Остается нарисовать возмущенную скоростями текстуру. Формировать новую картинку будем в массив pixel[].
-(void) renderWater
{
size_t width = nx*2;
size_t height = ny*2;
size_t bytesPerRow = 4*width;
memset (pixel, 0, bytesPerRow*height);
float zz = -1.9;
for (int j=0; j
В каждой точке вычисляется смещение от начальной картинки и интерполируется на текущую. Интерполяция нужна для того, чтобы программа работала и на iPhone 4S. Для этого я в два раза уменьшил размер текстуры по каждому направлению и в 4 раза повысил скорость алгоритма. На шестом айфоне этого делать не надо, он справляется с сеткой 160 на 284. Плюс, в зависимости от скорости воды в данной точке я меняю прозрачность текстуры от 0 до 255. Все. Этот цикл неплохо работает даже на старом iPhone 4S с частотой 20 кадров в секунду. Заключение
Вождение вилами по воде
[embedded content]
Результат моделирования также можно увидеть в двух приложениях под iPad и еще в двух под iPhone. Всех хороших выходных и светлая память нашим предкам.
Приложение Haken.
Приложение Frogger.
