FreeCAD — новый метод рисования02.09.2018 01:03

Disclamer: Я никогда в своей жизни не работал с CAD/CAM приложениями раньше, и, вдруг, пришлось. Принципы работы FreeCAD меня так восхитили, что это требует срочного поста на Хабр, чтобы рассказать другим.

Написанное в этом посте, вероятнее всего, будет тривиальным и скучным для большинства активных пользователей CAD, и этот пост нацелен в первую очередь на не-пользователей CAD с целью рассказать им про чудный новый мир компьютерной графики.

У меня возникла простая задача — сделать 3D модель своей квартиры. Не просто «стенки в размер», а все балки, выступы и загибы. Я попробовал одну, вторую, третью программу… Я отчаялся (началось с SweetHome3D, а закончилось blender и inkscape). Они все были чертовски неудобными. Среди программ, которые я попробовал, был и FreeCAD, который я пропустил по причине «нифига не делать» и «не работает толком». После того, как я отчаялся, я ещё раз пошёл по второму кругу. На этот раз, чуть больше читая документацию… И FreeCAD не только «взлетел», но и ещё и открыл для меня восхитительный новый мир точного векторного рисования, основывающегося на Constrains.

Для начала я расскажу про ту боль, от которой я страдал в разных редакторах.

Начнём с SweetHome3D. Условно-понятный интерфейс, позволяющий описать комнату как «пол» (где задаётся форма и выступы), вокруг которой делается «стена». SweetHome3D дал мне две проблемы: пиксельхантинг (размер меняется либо микроскопическими сдвигами мыши, либо в диалоге, но не существует метода «прижать» стенку к полу с точностью — только пиксельхантинг. Вторая проблема — модель SweetHome3D не подразумевает существование балок, арок и других элементов стены, не идущих сверху до низу. Дополнительно, SH3D не умеет наклонных стен и полов (я бы хотел, чтобы такой проблемы у меня не было, но перед тем, как эту проблему устранять IRL, её надо задокументировать). Т.е. SH3D покрывает 90% того, что мне было нужно, доставляя невероятную боль с 5%, и делая невозможным оставшиеся 5%.

Blender теоретически позволяет сделать всё, но только теоретически. На практике либо моих навыков не хватало, либо сам процесс очень медлительный, но нарисовав три с половиной угла, я сдался. Слишком медленно и слишком много возни с освещением и другими неважными вещами. Плюс (насколько я знаю), Blender вряд ли сможет показать нормальные 2D проекции с размерами.

Inkscape был хорош кроме одной проблемы — в многосекционной линии (F2) невозможно задать размеры каждой секции. Можно было бы — я бы всё в Inkscape так и рисовал.

… Но мой пост не про абсолютное превосходство FreeCAD над Blender (я в обоих их новичок и толком сравнить не могу), а про новый стиль рисования. Сначала про проблемы старого стиля (то есть «обычного» векторного рисунка).

Перед тем, как перейти к картинкам и объяснению идеи Constrains, я хочу сфокусироваться на нескольких проблемах, которые извечно преследуют векторные рисунки:

Почти объединённые кривые. Если две кривые почти соприкасаются, то можно подумать, что они соприкасаются. В какой-то момент (при печати, либо при дальнейших манипуляциях), картинка развалится.
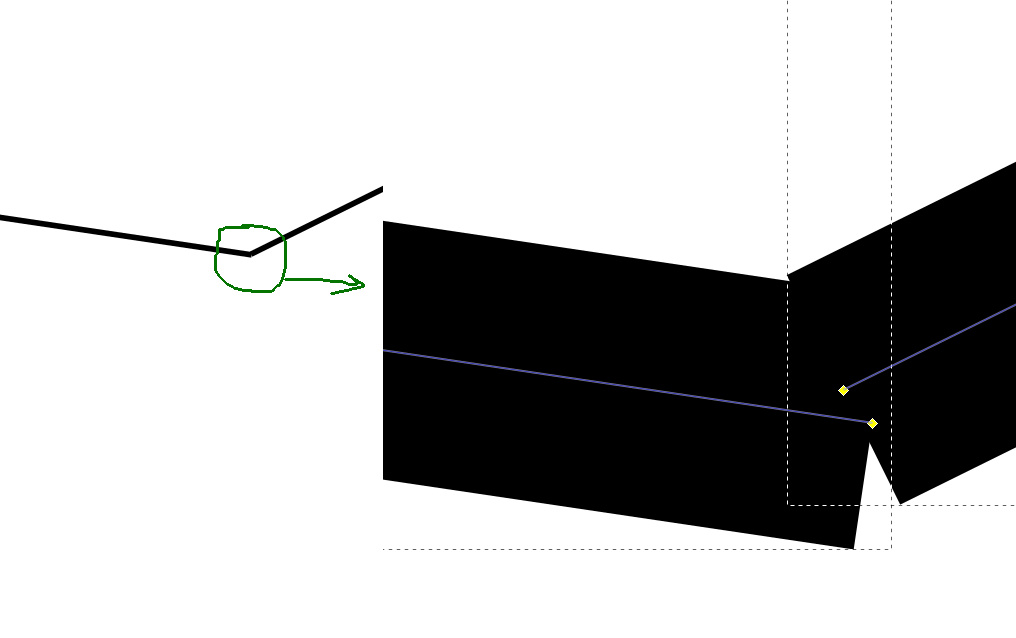
Почти параллельные/перпендикулярные линии. Они параллельны, но не до конца.

обратите внимание на outline, он показывает, что описывающий прямоугольник для двух линий больше самой линии, т.е. линия под острым углом.

производная от предыдущего — линии, стыкующиеся под углом в 0.001°.
неточности в размерах и толщине линий. Линия имеет свою толщину, и при редактировании (поворотах, ресайзах и т.д.) толщина начинает плыть. Более того, в большинстве векторных реакторов трудно нарисовать квадрат с площадью 100 и линией толщиной 0.5 (потому что линия на 50% заходит на площадь фигуры, и мы имеем не 10×10 внутри, а 9.75×9.75).
Сохранение align’а и симметрии является задачей, требующей постоянного внимания.

В редакторах встроено множество инструментов для борьбы с подобными неприятностями, но у этих инструментов есть одно затруднение — их надо осмысленно применять там, где возникла проблема. А за возникновением проблем надо следить самому.

Это было долгое вступление. Теперь я рассказываю про constrains, или, по-русски, удерживающие связи (перевод термина из статьи про степени свободы в механике.

Давайте попробуем нарисовать квадрат со стороной 10, опираясь на его фундаментальные свойства.

У квадрата 4 прямые стороны.

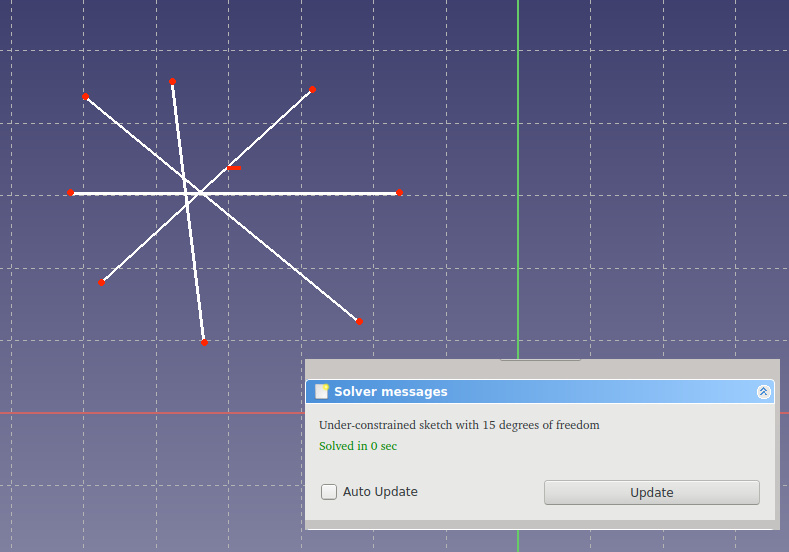
Почти получилось. Солвер подсказывает, что нам надо задать 15 дополнительных удерживающих связей, чтобы наша фигура была однозначной (у неё было 0 степеней свободы).

Противоположные стороны квадрата параллельны *

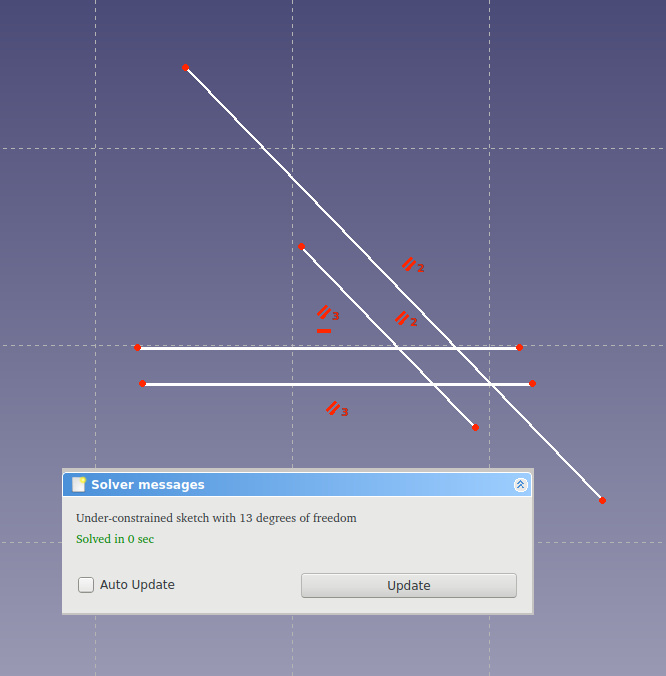
Солвер говорит, уже лучше. Стало не хватать 13. Обратите внимание на красные пометки — это указание на constrains. В самом начале у нас случайно получилось два ограничения — две горизонтальные линии.

Стало лучше, хотя на квадрат это всё ещё похоже мало. Что же не так? Ах, да, квадрат — это полигон, а у полигона стороны сходятся в углах в точку. Добавим эти ограничения.

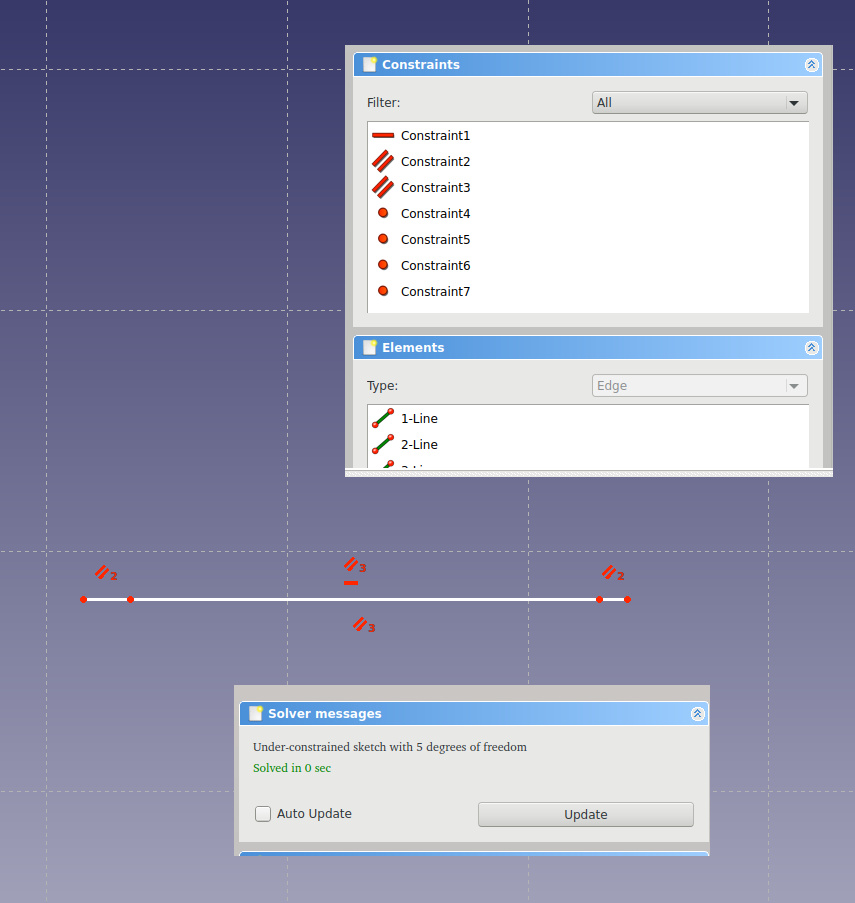
Получилось немного неожиданно, хотя solver всё более довольный. Указанная фигура — обычный такой четырёхугольник, в котором стороны попарно параллельны. Немного за пределами школьного курса, но вполне понятно.

Добавим объёма… плоскости к этой фигуре. Соседние грани — перпендикулярны.

Уже похоже на правду (хотя это я чуть-чуть подтянул вверх рисунок, потому что стороны нулевого размера вполне устраивают solver как перпендикулярные к прямой, на которой лежат (в виде точки)). solver ругается на избыток ограничений. Согласимся с ним и удалим одну перпендикулярность (у нас требование попарной параллельности, перпендикулярность для одной пары автоматически вытекает из перпендикулярности первой пары). После того, как мы удалили лишнее, solver жалуется на 4 свободы.

Запретим ещё что-нибудь, так как свободы слишком много.

Например, скажем, что все стороны должны быть одинакового размера. Достаточно сделать это для двух любых смежных сторон, и из этого вытекает, что все стороны равны (школьная геометрия!).

После этого у нас получается три свободы. Ещё три свободы? Но квадрат же… Да, это квадрат, но мы не знаем его размера (0 — тоже размер, между прочим), и положения в пространстве.

Зададим его — укажем, что один из углов квадрата лежит на точке »0, 0», плюс зададим для одной из сторон размер в 10 мм.

Всё, квадрат полностью готов, у него нет свобод, а значит, нет и скрытых ошибок.

Этот пример был немного гротескным, но, как я надеюсь, выразительным. Особенно меня впечатлило, что solver не только проверяет на отсутствие неоднозначностей, но ещё и предупреждает, если фигура содержит больше ограничений, чем надо.

Для меня такой метод описания рисунка является совершенно новым и неожиданным. В каком-то смысле он напоминает то, что делают типизированные языки программирования с машинным кодом — добавляют в него ограничений, позволяющих в математически-точной форме задать ограничения на возможные операции с данными. В тот момент, когда ограничений достаточно много, мы получаем однозначное решение, которое точно есть и точно однозначное. И точно правильное, если входные данные были правильными. И никаких «случайно задел мышкой» или «рука дрогнула».