Формализм Лагранжа в задачах с сухим трением
Данная статья являет собой логическое продолжение темы, начатой в предыдущей публикации. Как и было обещано в комментариях, рассмотрим применимость метода избыточных координат к динамическому анализу механических систем движущихся под действием сил сухого кулоновского трения. В качестве иллюстративного примера решим следующую задачу
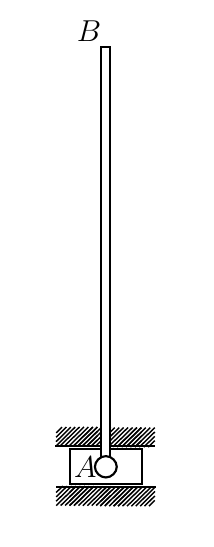
Тонкий однородный стержень массы m = 2 кг, длины AB = 2l = 1 м в точке A шарнирно прикреплен к невесомому ползуну, перемещающемуся в горизонтальных шероховатых направляющих. В начальный момент времени стержень расположен вертикально, затем его отклоняют от вертикали на ничтожно малый угол и отпускают без начальной скорости. Необходимо составить уравнения движения данной механической системы и найти закон её движения. Коэффициент трения между ползуном и направляющими равен f = 0,1.
Прежде чем приступить к решению задачи предлагаемым автором методом, рассмотрим немножко элементарной теории, касающейся сухого трения.
Нет более страшного наказания для механика, чем сила трения. Появляясь в задаче, эта сила сразу делает её существенно нелинейной, ибо ведет себя достаточно интересным образом.
Рассмотрим довольно простой пример. Пусть на шероховатой поверхности покоится горизонтальный брусок.
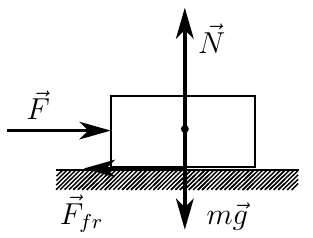
Пусть в начале к нему не прилагают никаких сил (кроме силы тяжести и нормальной реакции). В этом случае и сила трения между бруском и плоскостью будет равна нулю.
Теперь приложим к бруску небольшую горизонтальную силу. Брусок не сдвинется с места, так как в ответ на наше воздействие со стороны поверхности на него станет действовать сила трения, которая будет удовлетворять условию
Будем постепенно увеличивать силу и, согласно (1) расти будет и сила трения, которая в этом случае называется силой трения покоя. Так будет продолжаться до тех пор, пока сила трения покоя не достигнет величины
называемой предельной величиной силы трения покоя. Здесь f — коэффициент сухого трения между бруском и плоскостью; N — нормальная реакция со стороны плоскости. После этого сила трения расти перестанет, а при дальнейшем увеличении горизонтальной силы начнется скольжение бруска. Сила трения перейдет в силу трения скольжения, равную
где — скорость бруска.
Пример весьма тривиальный, однако он раскрывает суть поведения силы сухого трения. Таким образом, получаем следующий алгоритм расчета силы трения:
Если точка, где приложена сила трения неподвижна:
Расчитываем силу трения покоя и нормальную реакцию
Проверяем условиепри нарушении которого принимаем силу трения равной предельной силе трения покоя
Если точка приложения силы трения движется: Вычисляем нормальную реакцию
Вычисляем силу трения скольжения, согласно выражению (2)
Теперь решим нашу задачу. Рассматриваемая нами система имеет две степени свободы, однако из-за необходимости определения нормальной реакции расширяем число степеней свободы до трех и получаем следующую расчетную схему
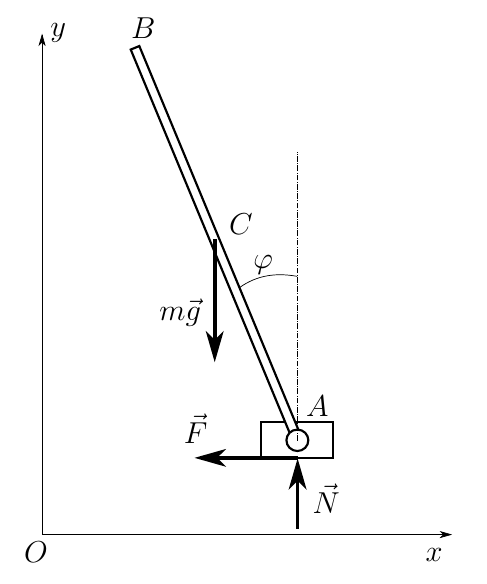
Здесь в качестве обобщенных координат берем вектор
где x, y — координаты точки A; — угол наклона стержня к вертикали. Вооружаемся Maple’ом
# Чистим память restart; # Подключаем линейную алгебру with (LinearAlgebra): # Подключаем лагранжеву механику read `/home/maisvendoo/work/maplelibs/mechanics/lagrange.m`: Определяемся с кинематикой системы
# Обобщенные координаты системы q:= [x (t), y (t), phi (t)]: # Координаты точки A xA:= q[1]: yA:= q[2]: # Координаты центра масс стержня xC:= q[1] — L*sin (q[3]): yC:= q[2] + L*cos (q[3]): # Радиус-векторы точек A и C rA:= Vector ([xA, yA]): rC:= Vector ([xC, yC]): # Вычисляем скорость ценра масс стержня VectorCalculus[BasisFormat](false): vC:= VectorCalculus[diff](rC, t): Вычисляем её кинетическую энергию
# Момент инерции стержня относительно центра масс
J:= m*(2*L)^2/12:
# Кинетическая энергия системы
T:= simplify (J*diff (q[3], t)^2/2 + m*DotProduct (vC, vC, conjugate=false)/2);
Maple выдает такой результат
Довольно громоздко, но «ковырять» нам не руками на листочке, поэтому двигаемся дальше. Задаем векторы и точки приложения сил
# Векторы сил, приоложенных к системе Mg:= Vector ([0, -m*g]): # Сила тяжести F_A:= Vector ([-F, 0]): # Сила трения N_A:= Vector ([0, N]): # Нормальная реакция # Формируем массив сил Fk:= [Mg, F_A, N_A]: # Формируем массив точек приложения сил rk:= [rC, rA, rA]: Получаем уравнения движения системы в форме Лагранжа 2 рода
# Составляем уравнения Лагранжа 2 рода
EQs:= LagrangeEQs (T, q, rk, Fk):
Получаем трёх «крокодилов»
Эти уравнения пришлось вбить в статью руками, ибо «копипаста» LaTeX-вывода Maple приводит к неприглядному виду результата. Но даже так видно — уравнения сложны и с учетом того что F — это сила трения, аналитически не интегрируемы.
Теперь введем уравнения связей. Во-первых, ползун движется по горизонтальным направляющим, поэтому
Кроме того, в том случае когда ползун неподвижен, а сила трения покоя не превысила предельного значения, включается ещё одна связь
где — некоторая горизонтальная координата ползуна. Теперь преобразуем систему (4) — (6) с учетом уравнений (7) и (8) и найдем силу трения покоя и нормальную реакцию
# Уравнения связей link_eq1:= q[1] = A: # Ползун неподвижен, если сила трения — сила трения покоя link_eq2:= q[2] = 0: # Ползун движется вдоль оси X Link_EQs:= {link_eq1, link_eq2}:
# Трансформируем систему для поиска силы трения покоя и нормальной реакции Reduced_EQs:= ReduceSystem (EQs, Link_EQs, q): solv_reduced:= SolveAccelsReacts (Reduced_EQs, [q[3]], [F, N]): # Выделяем силы из решения for i from 1 to numelems (solv_reduced) do if has (solv_reduced[i], F) then F1:= rhs (solv_reduced[i]); end if; if has (solv_reduced[i], N) then N1:= rhs (solv_reduced[i]); end if; end do: Тут приведу результат непосредственно выданный Maple
Если посмотреть на полученные выражения, то они вполне соответствуют логике процесса. Теперь получим выражение для расчета нормальной реакции в случае, когда ползун скользит по направляющим, учитывая, что в этом случае сила трения будет определятся выражением
(минус уже имеется в уравнениях движения)
# Трансформируем систему для поиска нормальной реакции при скольжении ползуна Slade_EQs:= ReduceSystem (EQs, {link_eq2}, q): # Силу трения принимаем равной силе трения скольжения for i from 1 to numelems (Slade_EQs) do Slade_EQs[i] := subs (F = f*N*signum (diff (q[1], t)), Slade_EQs[i]); end do: solv_slade:= SolveAccelsReacts (Slade_EQs, [q[1], q[3]], [N]): # Выделяем нормальную реакцию из решения for i from 1 to numelems (solv_reduced) do if has (solv_slade[i], N) then N2:= rhs (solv_slade[i]); end if; end do: М-да, «крокодилище» вышел ещё тот, особенно с учетом что Maple таки довольно избыточно генерирует LaTeX-код
Все необходимые нам выражения получены, теперь можно переходить к моделированию. В отличие от задачи с маятником, о которой я уже писал, тут мы честно трансформируем наши уравнения Maple-средствами для вида пригодного к численному решению. Прежде всего решим уравнения (4) — (6) относительно обобщенных ускорений
# Разрешаем основную систему уравнений относительно обобщенных ускорений Main_EQs:= SolveAccelsReacts (EQs, q, []):
# Число обобщенных координат s:= numelems (q): Результат уже не буду приводить — он тоже довольно громоздкий. Перейдем к фазовым координатам # Воводим фазовые координаты # Y[1] → x (t) # Y[2] → y (t) # Y[3] → phi (t) # Y[4] → vx (t) — горизонтальная проекция скорости ползуна # Y[5] → vy (t) — вертикальная проекция скорости ползуна # Y[6] → omega (t) — угловая скорость стержня
# Переходим к фазовым координатам в выражениях для реакций и трения покоя for i from 1 to s do N2:= subs (diff (q[i], t) = y[i+s], N2); N2:= subs (q[i] = y[i], N2); N1:= subs (diff (q[i], t) = y[i+s], N1); N1:= subs (q[i] = y[i], N1); F1:= subs (diff (q[i], t) = y[i+s], F1); F1:= subs (q[i] = y[i], F1); end do: # Переходим к фазовым координатам в уравнения движения for i from 1 to s do for j from 1 to s do eq:= Main_EQs[j]; if has (eq, diff (diff (q[i], t), t)) then accel[i] := rhs (eq); end if; end do; for j from 1 to s do accel[i] := subs (diff (q[j], t) = y[j+s], accel[i]); accel[i] := subs (q[j] = y[j], accel[i]); end do: end do: Формируем функции вычисления необходимых нам сил
# Вычисление нормальной реакции при покоящемся ползуне GetN1:= proc (mass, length, grav_accel, fric_coeff, Y) local react:= subs (m = mass, L = length, g = grav_accel, f = fric_coeff, N1); local i; for i from 1 to numelems (Y) do react:= subs (y[i] = Y[i], react); end do: return evalf (react); end proc: # Вычисление нормальной реакции при скользящем ползуне GetN2:= proc (mass, length, grav_accel, fric_coeff, Y) local react:= subs (m = mass, L = length, g = grav_accel, f = fric_coeff, N2); local i; for i from 1 to numelems (Y) do react:= subs (y[i] = Y[i], react); end do: return evalf (react); end proc: # Вычисление силы трения покоя GetF1:= proc (mass, length, grav_accel, fric_coeff, Y) local react:= subs (m = mass, L = length, g = grav_accel, f = fric_coeff, F1); local i; for i from 1 to numelems (Y) do react:= subs (y[i] = Y[i], react); end do: return evalf (react); end proc: Приведенный код хоть и объемный, но довольно прост — выполняется подстановка численных параметров в соответствующие выражения и их вычисление. Такую же функцию формируем и для вычисления обобщенных ускорений # Вычисление вектора обобщенных ускорений GetAccel:= proc (mass, length, grav_accel, fric_force, normal_react, Y) local acc; local i, j; for i from 1 to numelems (Y)/2 do acc[i] := subs (m = mass, L = length, g = grav_accel, F = fric_force, N = normal_react, accel[i]); end do: for i from 1 to numelems (Y)/2 do for j from 1 to numelems (Y) do acc[i] := evalf (subs (y[j] = Y[j], acc[i])); end do: end do: return [seq (acc[i], i=1…numelems (Y)/2)]; end proc: Задаем параметры, данные нам в условии задачи
# Задаем параметры системы m1:= 2.0; L1:= 0.5; f1:= 0.1; g1:= 9.81; Время задать основную логику модели, которая определяет расчет силы трения. При этом задаемся погрешностью скорости ползуна, при которой будем считать её равной нулю.
# Вычисление силы трения и нормальной реакции GetFricNormal:= proc (mass, length, grav_accel, fric_coeff, Y) local F1, N1; # Сила трения и нормальная реакция local eps_v:= 1e-6; # Точность нуля скорости ползуна # Если ползун неподвижен if abs (Y[4]) < eps_v then # Вычисляем силу трения покоя и нормальную реакцию F1 := GetF1(mass, length, grav_accel, fric_coeff, Y); N1 := GetN1(mass, length, grav_accel, fric_coeff, Y); # Если трение покоя превышает максимально возможное значение, # то сила трения равна силе трения скольжения if abs(F1) > fric_coeff*abs (N1) then F1:= fric_coeff*abs (N1)*signum (F1); end if; else # Если ползун уже движется, считаем нормальную реакцию и трение скольжения N1:= GetN2(mass, length, grav_accel, fric_coeff, Y); F1:= fric_coeff*abs (N1)*signum (Y[4]); end if; return [F1, N1]; end proc: Определяем callback для решателя
# Вычисление правой части ОДУ в форме Коши для численного решателя (собственно математическая модель) EQs_func:= proc (N, t, Y, dYdt) local F1, N1; # Сила трения и нормальная реакция local acc; # Обобщенные ускорения local ret; # Вычисляем силу трения и нормальную реакцию ret:= GetFricNormal (m1, L1, g1, f1, Y); F1:= ret[1]; N1:= ret[2]; # Вычисляем производные фазовых координат acc:= GetAccel (m1, L1, g1, F1, N1, Y); dYdt[1] := Y[4]; dYdt[2] := Y[5]; dYdt[3] := Y[6]; dYdt[4] := acc[1]; dYdt[5] := acc[2]; dYdt[6] := acc[3]; end proc: Формируем для решателя список фазовых координат и начальные условия (угол отклонения стержня от вертикали делаем малым) и выполняем численное интегрирование (на самом деле последний вызов dsolve () лишь обозначает наши намерения по численному решению — оно будет поизведено при вычислении конкретных значений фазовых координат). # Список фазовых координат vars:= [X (t), Y (t), Phi (t), Vx (t), Vy (t), Omega (t)]; # Начальные условия initc:= Array ([0.0, 0.0, 1e-4, 0.0, 0.0, 0.0]); # Интгрируем уравнения dsolv:= dsolve (numeric, number = 6, procedure = EQs_func, start = 0, initial = initc, procvars = vars, output=listprocedure); Выполняем некоторые подготовительные операции # Выделяем нужную нам часть решения x:= eval (X (t), dsolv); y:= eval (Y (t), dsolv); phi:= eval (Phi (t), dsolv); vx:= eval (Vx (t), dsolv); vy:= eval (Vy (t), dsolv); omega:= eval (Omega (t), dsolv); Далее просчитаем движение системы в течение некоторого интервала времени и сформируем массивы данных для вывода на графики # Рассчитываем движение системы на интересующем нас интервале времени t0:= 0.0: t1:= 10.0: num_plots:= 1000: dt:= (t1 — t0)/num_plots: t:= t0: i:= 1: while t <= t1 do Time[i] := t; Y := [x(t), y(t), phi(t), vx(t), vy(t), omega(t)]; x1[i] := Y[1]; phi1[i] := Y[3]; fric[i] := GetFricNormal(m1, L1, g1, f1, Y)[1]; norm_react[i] := GetFricNormal(m1, L1, g1, f1, Y)[2]; lim_fric[i] := f1*abs(norm_react[i])*fric[i]/abs(fric[i]); t := t + dt; i := i + 1; end do: Ну вот, у нас практически всё готово # Формируем графики G_x := [ [Time[k],x1[k]] $k=1..num_plots]: G_phi := [ [Time[k],phi1[k]] $k=1..num_plots]: G_fric := [ [Time[k],fric[k]] $k=1..num_plots]: G_norm_react := [ [Time[k],norm_react[k]] $k=1..num_plots]: G_lim_fric := [ [Time[k],lim_fric[k]] $k=1..num_plots]:
# Выводим их на экран gr_opts:= captionfont=['ROMAN', 16], axesfont=['ROMAN','ROMAN', 12], titlefont=['ROMAN', 14], gridlines=true: plot (G_x, gr_opts, view=[t0…t1, -1…1.0]); plot (G_phi, gr_opts, view=[t0…t1, 0.0…7.0]); plot ({G_fric, G_lim_fric}, gr_opts, view=[t0…t1, -20…20]); plot (G_norm_react, gr_opts, view=[t0…t1, 0.0…200.0]); Получаем графики. Красоты ради, графики были конвертированы из Maple в *.eps и немножко обработаны в inkscape.
Перемещение ползуна Угол отклонения стержня от вертикали
Угол отклонения стержня от вертикали Сила трения
Сила трения Здесь синей линией показано предельное значение трения покоя, а красной — фактическое значение силы трения.
Здесь синей линией показано предельное значение трения покоя, а красной — фактическое значение силы трения.
Нормальная реакция со стороны направляющих
Видно, что ползун покоится в течение чуть более двух секунд, а затем, после преодоления трения покоя приходит в движение, которое постепенно затухает и полностью прекращается через 6,5 секунд после начала движения. После этого сила трения никогда не превышает предельного для покоя значения, ползун остается на месте, а стержень совершает гармонические колебания около устойчивого положения равновесия.
Рассмотрено применение метода избыточных координат и уравнений Лагранжа 2 рода к анализу движения систем с сухим трением. Видно, что при внешней громоздкости получаемых результатов, процес синтеза уравнений движения может быть автоматизирован средствами символьной математики, а это существенно для современных технических задач.
Благодарю за внимание к моему труду.
