Фильтр Калмана: разбор навигационной системы БПЛА + исходный код
В статье я бы хотел объяснить принципиальную разницу между Фильтром Калмана (ФК) и классическими фильтрами, кратко рассмотреть преимущество выбранного ФК поделиться опытом использования данного ФК во встраиваемой системе квадрокоптера для навигации на основе инерциального и ГНСС датчиков и поделится исходным кодом с демкой для самостоятельного изучения.
Всем привет! Меня зовут Илья, я работаю программистом-инженером в компании «SID Logic», мы занимаемся разработкой электроники и сопутствующего ПО для различных применений, мои области интересов касаются систем навигации (оптические, инерциальные, ГНСС, UWB, GSM/LTE), систем управления (ПИД, MRAC, MPC) преимущественно для задач робототехники, беспилотников. Одну из важных тем в навигации занимает тема Фильтра Калмана.
На Хабре Фильтру Калману (ФК) посвящено уже много статей, но я пока не встречал объяснения (возможно плохо смотрел?:))принципиальной преимущества его использования перед например альфа-бета, различными комбинациями фильтров низкой частоты (ФНЧ), фильтров высокой частоты (ФВЧ), интеграторами, дифференциаторами и т.д… Однако даже если вы знали, то о чем я буду дальше говорить, возможно вам будет полезен код, которым я пользуюсь уже несколько лет, на основе которого было проверено множество гипотез, подтверждено их применение.
Теоретическому объяснению основ посвящено уже много статей, поэтому не будем касаться этой темы, а попробуем разобраться в сути алгоритма с инженерной, прикладной точки зрения.
Для начала нужно рассмотреть такую формулировку задачи. Абстрактной задачи.
Представьте у вас есть большой пульт с вращающимися крутилками, а на выходе некоторая температура, у вас есть таблица по каждой крутилке, как каждая крутилка влияет на температуру. Но нет обратной формулы — какие положения у крутилок должны быть, чтобы установить необходимую температуру. И вам говорят, что нужно выставить определенную температуру, после чего вы начинаете подкручивать крутилки, одну вторую, третью, туда-сюда, пока наконец не установите нужную температуру.
Или другой пример, более реальной задачи — у вас есть 2 фотографии, сделанные под разным углом (части панорамы), вы открываете фотошоп и пытаетесь сместить второе фото так, чтобы с виду обе фотографии не имели разрыва между собой, иначе говоря пытаетесь сшить панораму.
 Сшивка панорамы
Сшивка панорамыВ обоих примерах вы можете регулировать переменные (крутилки и смещения фото) и смотреть как они влияют на результат, и вы можете оценить, как далеко вы от цели или близко (близка ли установленная температура к желаемой, сильно ли видно границу стыка двух фотографий). То есть у вас есть функция прямой зависимости (температура = f (крутилки) и визуальная сходимость стыка = f (смещение 2 фото)), но нет обратной зависимости.
Такого рода задачи возникают повсеместно в инженерной практике в любых областях — поиск оптимальной конструкции моста, поиск коэффициентов искажения линзы камеры для нивелирования данных искажений, оптимальное управление химическим процессом, картографирование, обучение нейросетей и т.д.
В общем случае поиск оптимальных (по какому- то критерию в математическом смысле) параметров математической модели это огромная отдельная область, где могут использоваться самые разные реализации в зависимости от кол-ва оптимизируемых параметров (веса нейросети, коэффициенты линзы камеры), требований к вычислительной сложности (микроконтроллеры, GPU кластеры), самой физической природы функции оптимизации (кол-во локальных минимум, их разброс в случае поиска минимума функции, ограничения и род величин).
Итак, Фильтр Калмана является частным упрощенным случаем большого семейства алгоритмов поиска оптимальных параметров и состояния системы на основе математической модели.
ФК помогает решать задачи:
преимущественно рассматриваемые в эволюции во времени;
с относительно малым количеством оптимизируемых параметров (относительно весов нейросетей например) до ~100;
имеющие глобальный минимум, то есть одно решение (с множеством локальных минимумов лучше справляется частичный фильтр Particle Filter например);
непрерывная природа величин параметров (не дискретная);
оптимизируемые параметры не должны иметь ограничений (например, масса не может быть отрицательной и для использования в ФК, должна быть специальная математическая модель).
Итак, основная мысль данной статьи, на которой я хотел бы акцентировать внимание:
Суть данного алгоритма — это поиск оптимальных значений (с точки зрения наименьших квадратов) состояния и параметров системы, которые бы удовлетворяли реальным измеренным данным и эволюции системы во времени. Связь состояния и параметров от модели измеряемых данных может быть нелинейной. При этом описать явно в аналитическом виде зависимость искомого состояния или параметра от измеряемой датчиком величины не всегда возможно.
Или проще говоря, ФК подбирает такие параметры, чтобы на выходе получить тоже самое, что показывают датчики, при этом не противореча предыдущим состояниям.
Будем работать с более применительным к реальности видом ФК — то есть нелинейным, так как большинство систем имеют нелинейные взаимосвязи.
Как и многие оптимизационные алгоритмы, нелинейные ФК должны понимать в какую сторону им нужно менять параметры, чтобы максимально приблизиться к минимуму функции (минимальное расхождение между предыдущим состоянием системы и минимальное расхождение между тем, что мы ожидаем увидеть от моделируемого датчика (модель датчика) и самими данными от реального датчика). Для этого им нужен виртуальный градиент (направление, двигаясь против которого можно достичь минимума функции). Поиск этого градиента зависит от вида линеаризации.
Все нелинейные виды ФК так или иначе используют линеаризацию. Распространены 2 вида линеаризации ФК:
Рассчитанные человеком матрицы Якоби записанные в аналитическом виде (Extented Kalman Filter EKF). Другими словами — это линеаризация по касательной.
Линеаризация методом пробных точек (Sigma Point Kalman Filter, Unscented Kalman Filter UKF). Другими словами — это линеаризация по секущей.
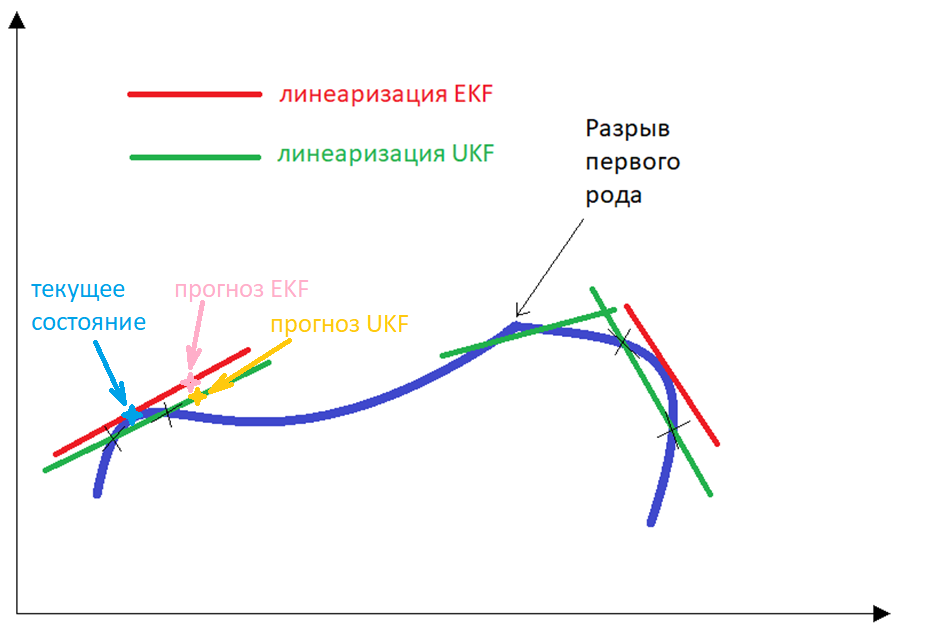 EKF и UKF линеаризации
EKF и UKF линеаризацииВ инженерном контексте для нас можно выделить следующие особенности:
В первом случае из преимуществ — быстрая скорость работы. Из недостатков — ручная запись в аналитическом виде матрицы Якоби, меньшая стабильность и точность на сильных нелинейных взаимосвязях, функции эволюции и модели датчика должны быть дифференцируемы.
Во втором случае из преимуществ — лучшая стабильность и точность на сильных нелинейных взаимосвязях, отсутствие необходимости записи матриц Якоби, нужна лишь запись в прямом виде эволюции и модели датчика.
Согласно целям статьи, понизить порог вхождения в тему, дать универсальный алгоритм для быстрого прототипирования и проверки гипотез в условиях слабой вычислительной базы и малого кол-ва памяти лучшим выбором будет являться второй вид ФК — UKF.
Помимо UKF, существуют следующие вариации сигма-точечного фильтра Калмана: CDKF (central difference Kalman filter — фильтр Калмана центральной разности), SRUKF (square-root unscented Kalman filter — ансцентный фильтр Калмана квадратного корня), SRCDKF (square-root central difference Kalman filter — фильтр Калмана квадратного корня центральной разности) и их итеративные модификации IUKF, ICDKF, ISRUKF, ISRCDKF, которые рассматриваются в работах [1, 2].
В инженерном контексте задачи оптимальным выбором я считаю т.н. Square Root Central Difference Kalman Filter (SRCDKF). Выбор сигма точек осуществляется согласно центральной разности (в отрицательное направление от линеаризуемой точки и в положительное направление) пропорционально матрице квадратного корня ковариации. При этом не используется разложение Холецкого для матрицы ковариации, которое может быть не стабильным в условиях с присутствием одновременно малых и больших значений в матрице.
Я решил не загромождать статью лишними формулами, кому будет интересно может почитать литературу в списке.
Это универсальное ядро SRCDKF, которое можно использовать в разных приложениях, реализуя разные математические модели.
Исходный код ядра можно скачать:
Ядро SRCDKF
С Теорией пока всё. Теперь практика.
Пример, иллюстрирующий суть ФК
Начнем сразу с реальной инженерной задачи, без примеров на одномерных случаях, так как в них не проявится вся мощь таких алгоритмов. Параллельно разберем исходный код.
Допустим, есть квадрокоптер, который может лететь в любую сторону, любой стороной борта, то есть у него нет переда или зада. На квадрокоптере установлен акселерометр и датчик угловой скорости (IMU), датчик глобальной навигационной системы (GNSS), в нашем примере нету магнитометра и барометра, хотя это не принципиально.
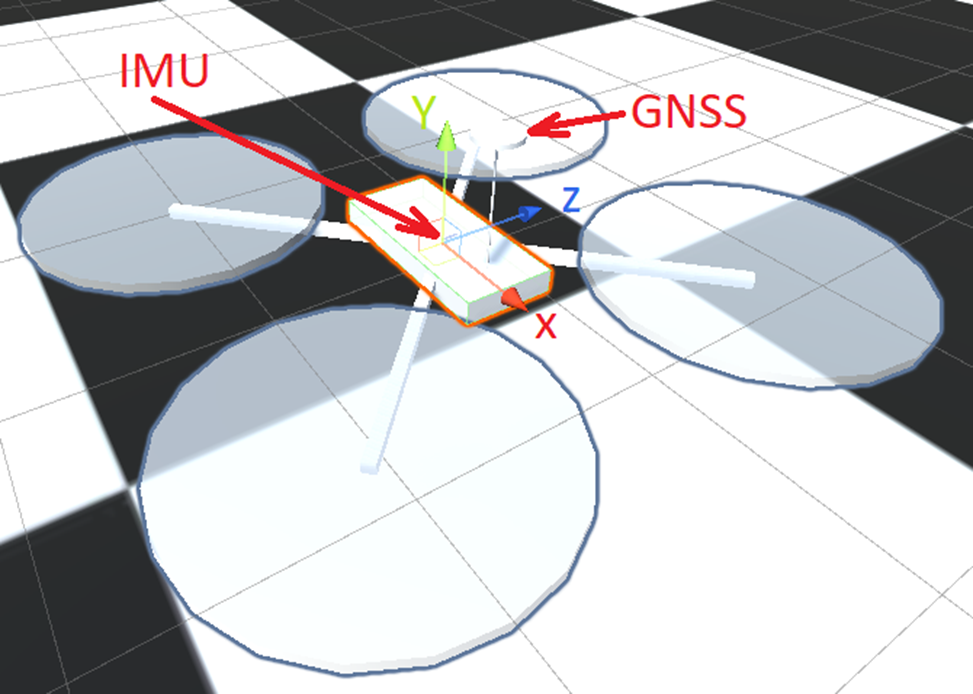
Нам для управления квадрокоптером нужно знать положение и ориентацию в пространстве в каждый момент времени.
Раз уж я сказал, что задача из реального мира, а реальный мир трехмерный, то мы будем рассматривать математическую модель описания вращения и положения в трехмерном пространстве. Для описания вращения в трехмерном пространстве воспользуемся кватернионом, можно сказать стандартом для таких случаев. А для описания положения — обычным 3-х мерным вектором.
Кто работал с дешевыми MEMS IMU знает о необходимости калибровки для нивелирования масштабных искажений, межосевых взаимосвязей, а также смещений (biases).
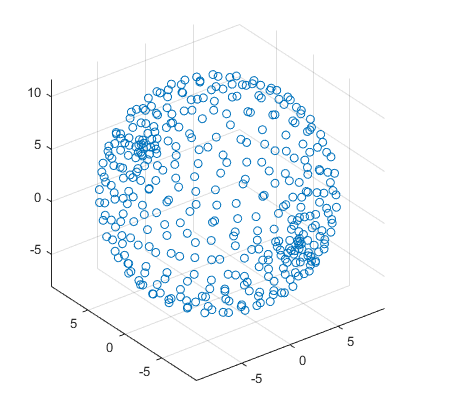 Так выглядят данные с акселерометра, при вращении по всем осям. Центр эллипсоида смещен на некоторый вектор (bias). Сам эллипсоид масштабно искажен.
Так выглядят данные с акселерометра, при вращении по всем осям. Центр эллипсоида смещен на некоторый вектор (bias). Сам эллипсоид масштабно искажен.Упрощенная, но достаточная для нашей точности математическая модель (без масштабных и межосевых коэффициентов) акселерометра и ДУСа одинаковая и имеет вид:
Где — 3-х мерный вектор данных непосредственно с сенсора (ускорения и угловой скорости соответственно),
— истинный 3-х мерный вектор данных,
— 3-х мерный вектор смещения (bias).
Модель IMU у нас есть.
Далее начинается творчество от которого зависит насколько точно, стабильно будет работать алгоритм. Нужно придумать математическую модель эволюции системы, то есть как она будет меняться со временем, какие данные от сенсоров будут являться моделируемыми, какие данные будут априорными, в какой системе координат будет выражаться вектор состояния (глобальной, привязанной к географическим осям север-восток или локальной, в системе координат квадрокоптера), какая модель датчика GNSS. На эту тему написано множество статей и реализовано множество математических моделей. Однако, чтобы не загромождать статью и не усложнять пример, я предлагаю воспользоваться не слишком сложной и в то же время рабочей математической моделью.
Для более-менее достаточной для нашей точности математической модели нужно 3 параметра для описания смещения (bias) акселерометра (в СК IMU), 3 параметра для описания смещения (bias) датчика угловой скорости (в СК IMU), 3 параметра описания положения (3-х мерный вектор в глобальной СК), 4 параметра для описания кватерниона ориентации (кватернион, выражающий вектор из СК коптера в глобальную СК), дополнительно включим 3-х мерный вектор скорости (в глобальной СК). Итого 16 параметров. Это называется вектор состояния системы, так как он описывает полное состояние (в контексте нашей задачи) нашего квадрокоптера в конкретный момент времени, то есть какое он имеет положение, ориентацию, скорость и т.д.
Эволюция системы описывается тем, как будет меняться вектор состояния во времени, то есть зависимость нынешнего момента времени от прошлого, еще этот этап называется прогнозом. — текущий момент времени,
— прошлый момент времени.
Здесь просто интегрируется по времени положение по скорости — шаг дискретизации.
— временный вектор ускорений, состоящий из
— вектора непосредственно из акселерометра
— смещение акселерометра в прошлый прогноз,
— операция вращения вектора кватернионом, в данном случае выражает локальный вектора ускорения в глобальную СК.
— кватернион в прошлый прогноз.
— вектор стандартных отклонений шумов прогноза для линейной скорости.
— вектор угловой скорости, состоящий из
— вектора данных непосредственно с ДУСа,
— рассчитанный на предыдущем шаге вектор смещения,
— вектор стандартных отклонений шумов прогноза для угловой скорости.
— символ, обозначающий перемножение кватернионов,
— это функция перевода 3-х мерного вектора вращения, находящегося в касательной плоскости относительно сферы кватерниона в пространство кватерниона, подробнее распишу попозже.
Смещения IMU не зависят от других переменных в векторе состояния, поэтому в нынешнем моменте времени они почти равны прошлым значениям. Почти, потому что все-таки они немного меняются со временем (температура может меняться), нужно чтобы ФК понимал, что это не константы и имел некоторую неопределенность в значении, для этого есть два параметра — которые являются векторами стандартных отклонений шумов прогноза для смещений IMU.
void TimeUpdate(float *in, float *noise, float *out, float *u, float dt, int n) {
float tmp[3], acc[3];
float rate[3];
float mat3x3[3 * 3];
float q[4];
int i;
float qRate[4], qRes[4];
// assume out == in
out = in;
for (i = 0; i < n; i++)
{
// create rot matrix from current quat
q[0] = in[UKF_STATE_Q1*n + i];
q[1] = in[UKF_STATE_Q2*n + i];
q[2] = in[UKF_STATE_Q3*n + i];
q[3] = in[UKF_STATE_Q4*n + i];
quatToMatrix(mat3x3, q, 1);
// pos
out[UKF_STATE_POSX*n + i] = in[UKF_STATE_POSX*n + i] + in[UKF_STATE_VELX*n + i] * dt;
out[UKF_STATE_POSY*n + i] = in[UKF_STATE_POSY*n + i] + in[UKF_STATE_VELY*n + i] * dt;
out[UKF_STATE_POSZ*n + i] = in[UKF_STATE_POSZ*n + i] + in[UKF_STATE_VELZ*n + i] * dt;
// acc
tmp[0] = u[0] + in[UKF_STATE_ACC_BIAS_X*n + i];
tmp[1] = u[1] + in[UKF_STATE_ACC_BIAS_Y*n + i];
tmp[2] = u[2] + in[UKF_STATE_ACC_BIAS_Z*n + i];
// rotate acc to world frame
rotateVecByMatrix(acc, tmp, mat3x3);
acc[1] -= GRAVITY;
out[UKF_STATE_VELX*n + i] = in[UKF_STATE_VELX*n + i] + acc[0] * dt + noise[UKF_V_NOISE_VEL_X*n + i];
out[UKF_STATE_VELY*n + i] = in[UKF_STATE_VELY*n + i] + acc[1] * dt + noise[UKF_V_NOISE_VEL_Y*n + i];
out[UKF_STATE_VELZ*n + i] = in[UKF_STATE_VELZ*n + i] + acc[2] * dt + noise[UKF_V_NOISE_VEL_Z*n + i];
// rate = rate + bias + noise
rate[0] = (u[3] + in[UKF_STATE_GYO_BIAS_X*n + i] + noise[UKF_V_NOISE_RATE_X*n + i]) * dt;
rate[1] = (u[4] + in[UKF_STATE_GYO_BIAS_Y*n + i] + noise[UKF_V_NOISE_RATE_Y*n + i]) * dt;
rate[2] = (u[5] + in[UKF_STATE_GYO_BIAS_Z*n + i] + noise[UKF_V_NOISE_RATE_Z*n + i]) * dt;
// rotate quat
exp_mapQuat(rate, qRate);
quatMultiply(qRes, q, qRate);
out[UKF_STATE_Q1*n + i] = qRes[0];
out[UKF_STATE_Q2*n + i] = qRes[1];
out[UKF_STATE_Q3*n + i] = qRes[2];
out[UKF_STATE_Q4*n + i] = qRes[3];
// acc bias
out[UKF_STATE_ACC_BIAS_X*n + i] = in[UKF_STATE_ACC_BIAS_X*n + i] + noise[UKF_V_NOISE_ACC_BIAS_X*n + i] * dt;
out[UKF_STATE_ACC_BIAS_Y*n + i] = in[UKF_STATE_ACC_BIAS_Y*n + i] + noise[UKF_V_NOISE_ACC_BIAS_Y*n + i] * dt;
out[UKF_STATE_ACC_BIAS_Z*n + i] = in[UKF_STATE_ACC_BIAS_Z*n + i] + noise[UKF_V_NOISE_ACC_BIAS_Z*n + i] * dt;
// gbias
out[UKF_STATE_GYO_BIAS_X*n + i] = in[UKF_STATE_GYO_BIAS_X*n + i] + noise[UKF_V_NOISE_GYO_BIAS_X*n + i] * dt;
out[UKF_STATE_GYO_BIAS_Y*n + i] = in[UKF_STATE_GYO_BIAS_Y*n + i] + noise[UKF_V_NOISE_GYO_BIAS_Y*n + i] * dt;
out[UKF_STATE_GYO_BIAS_Z*n + i] = in[UKF_STATE_GYO_BIAS_Z*n + i] + noise[UKF_V_NOISE_GYO_BIAS_Z*n + i] * dt;
}
}Пару слов о векторах стандартных отклонений шумов прогноза. Чем больше будут эти значения шумов, тем меньше доверие прогнозу, неопределенность соответствующей переменной вектора состояния будет расти с каждой итерацией прогноза и этап коррекции будет вносить существенную корректировку в них. То есть эта переменная будет подвержена большой волатильности. ФК будет пользоваться данной «крутилкой» больше, чем теми, у которых малое значение стандартного отклонения шума.
Также стоит отметить, что в отличие от других видов ФК модель шума (как процесса, так и датчика) может быть не аддитивной, и данный вид ФК сможет учесть и нелинейную природу шума. Это преимущество обеспечено способом линеаризации с помощью сигма-точек, которые пропускаются в том, числе и через модель шума.
По поводу . Кватернион — это гиперпараметризированная модель вращения, так как имеет 4 параметра в пространстве вращения с 3 степенями свободы. Так как полноценно описать вращение 3 параметрами не получается (Gimbal lock), приходится прибегать к таким математическим конструкциям, как кватернионы. Для перехода из 4-х мерного пространства в 3-х мерное пространство и обратно есть специальные операции
. Это можно представить как сферу (кватернион) и касательную плоскость (3-х мерный вектор вращения).
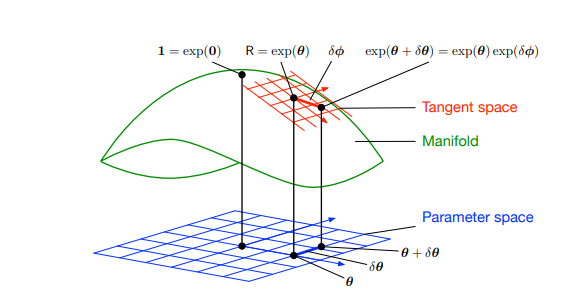
Отсюда же проистекает проблема, которую я описывал выше (ФК не умеет работать с параметрами, у которых есть ограничения), у кватерниона должна быть единичная длина. В таком случае можно пойти на небольшую хитрость и после каждой итерации прогноза нормализовывать кватернион. Для нашей мат модели такой способ сгодится, однако для более нелинейных систем, придется использовать специальную арифметику и операции с кватернионами внутри ФК. Подробнее про касательные пространства и фильтрацию с кватернионами в [3, 4].
В нашем случае есть только 2 датчика IMU и GNSS. IMU — используется непосредственно в модели прогноза как априорные значения и не моделируются.
GNSS моделируется так:
— кватернион из вектора состояния,
— вектор из IMU в GNSS в СК IMU,
— вектор позиции из вектора состояния,
— вектор стандартного отклонения шума GNSS.
Чем выше тем меньше доверие GNSS, данную величину можно варьировать в зависимости от качества данных с датчика.
void navUkfPosUpdate(float *u, float *x, float *noise, float *y) {
float vglov[3];
rotateVectorByQuat(vglov, &u[0], &x[UKF_STATE_Q1]);
y[0] = x[UKF_STATE_POSX] + vglov[0] + noise[0]; // return position
y[1] = x[UKF_STATE_POSY] + vglov[1] + noise[1];
y[2] = x[UKF_STATE_POSZ] + vglov[2] + noise[2];
}Вектора стандартных отклонений шумов прогноза и модели датчиков можно взять из даташитов, либо провести эксперимент с реальными датчиками, рассчитать самому. В нашем случае они уже рассчитаны, если захотите использовать другую мат. модель — будет от чего отталкиваться.
Кроме настоящих реальных датчиков, можно моделировать псевдодатчики. Например при старте, когда коптер еще не взлетел и мы точно уверены, что он не движется, можно использовать псевдоизмерения угловой и линейной скоростей, которые равны нулю. Тем самым сообщая ФК, что сейчас движения нет и эта информация в свою очередь поможет в уточнении вектора состояния.
Итак, для демонстрации данного ФК был написана демка на Unity.
Кратко расскажу подробности симулятора:
Сам ФК в Unity используется как динамическая библиотека, для WebGL — сырые исходники. Коптер не управляется по физическим законам, используются просто силы и моменты для имитации полета коптера в скрипте Control.cs. Для имитации IMU и GNSS созданы 2 скрипта IMUModel.cs и GNSSModel.cs. Обертка и взаимодействие с Unity ФК реализована в KalmanFilter.cs. Для графиков использовался открытый Asset.
Для физики используется внутренний движок PhysX. Для демонстрации 60 Гц — достаточно.
Вот видео демки и графики вектора состояния.
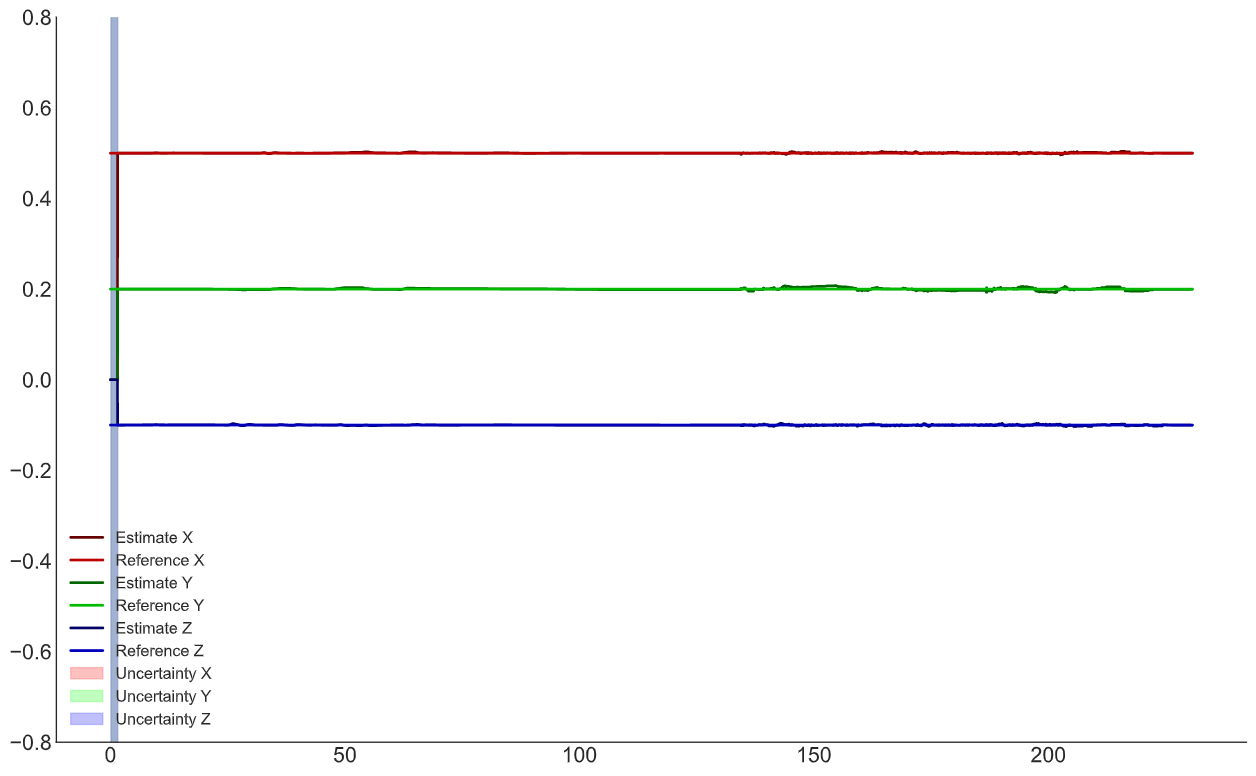 Вектор смещений ДУСа
Вектор смещений ДУСа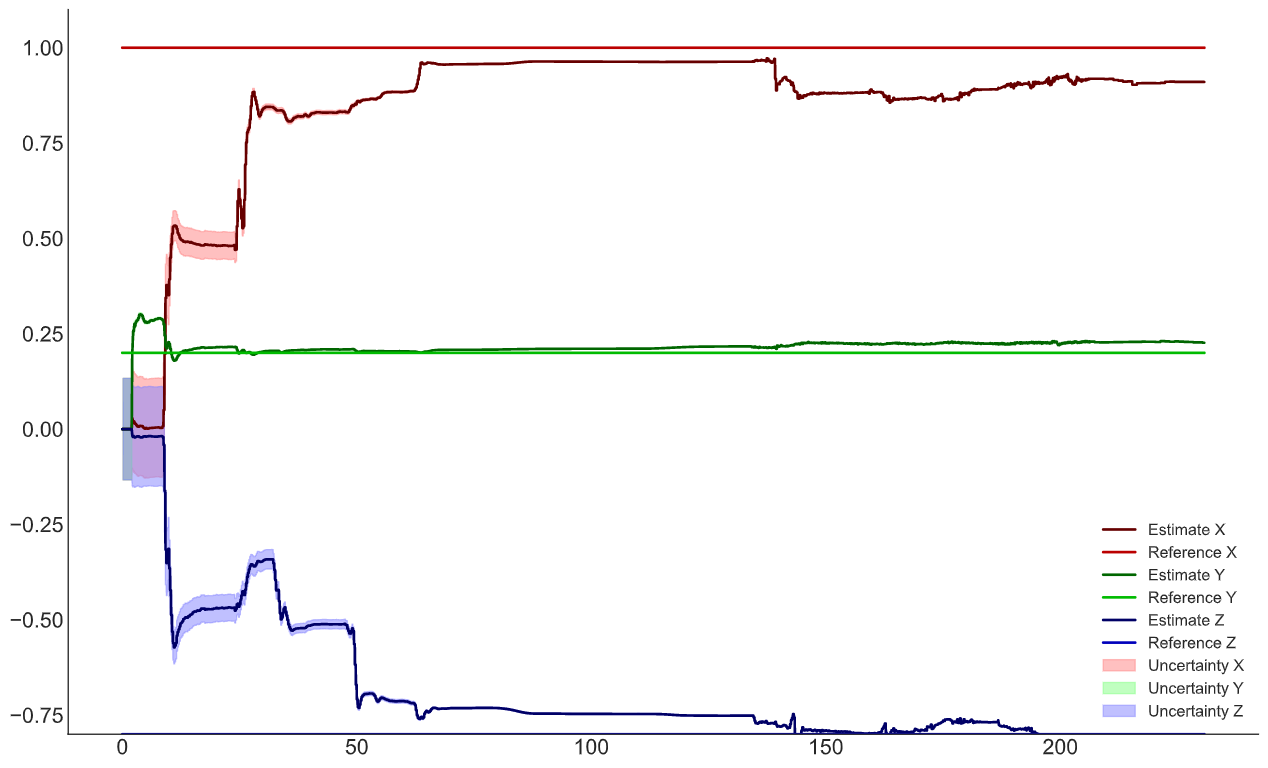 Вектор смещений акселерометра
Вектор смещений акселерометра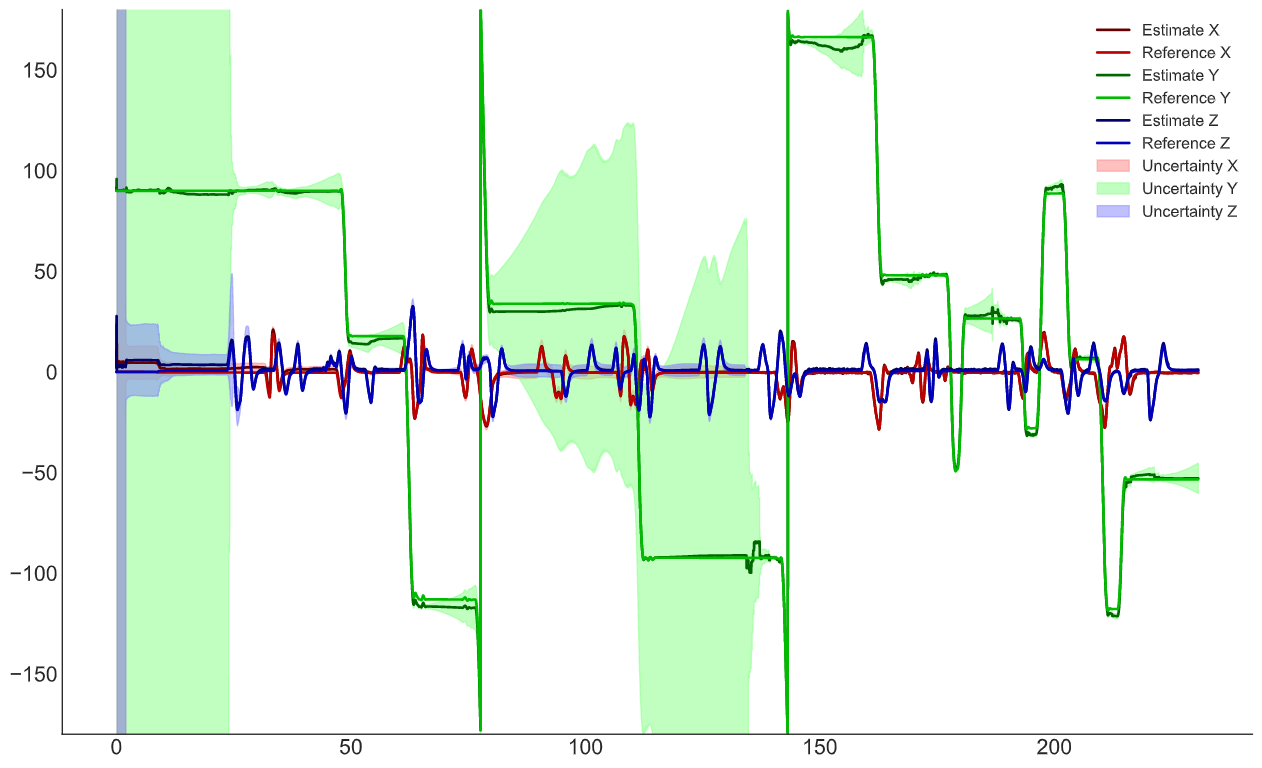 График углов Эйлера
График углов Эйлера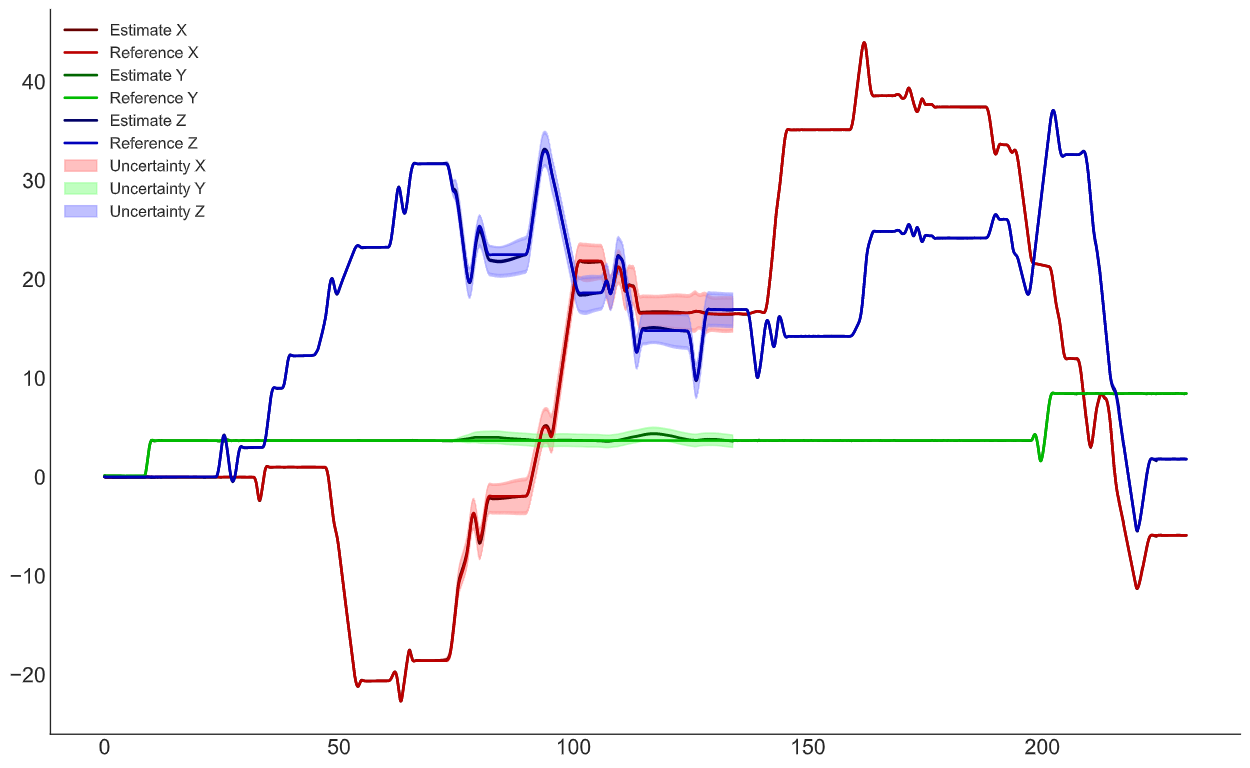 Вектор положения
Вектор положения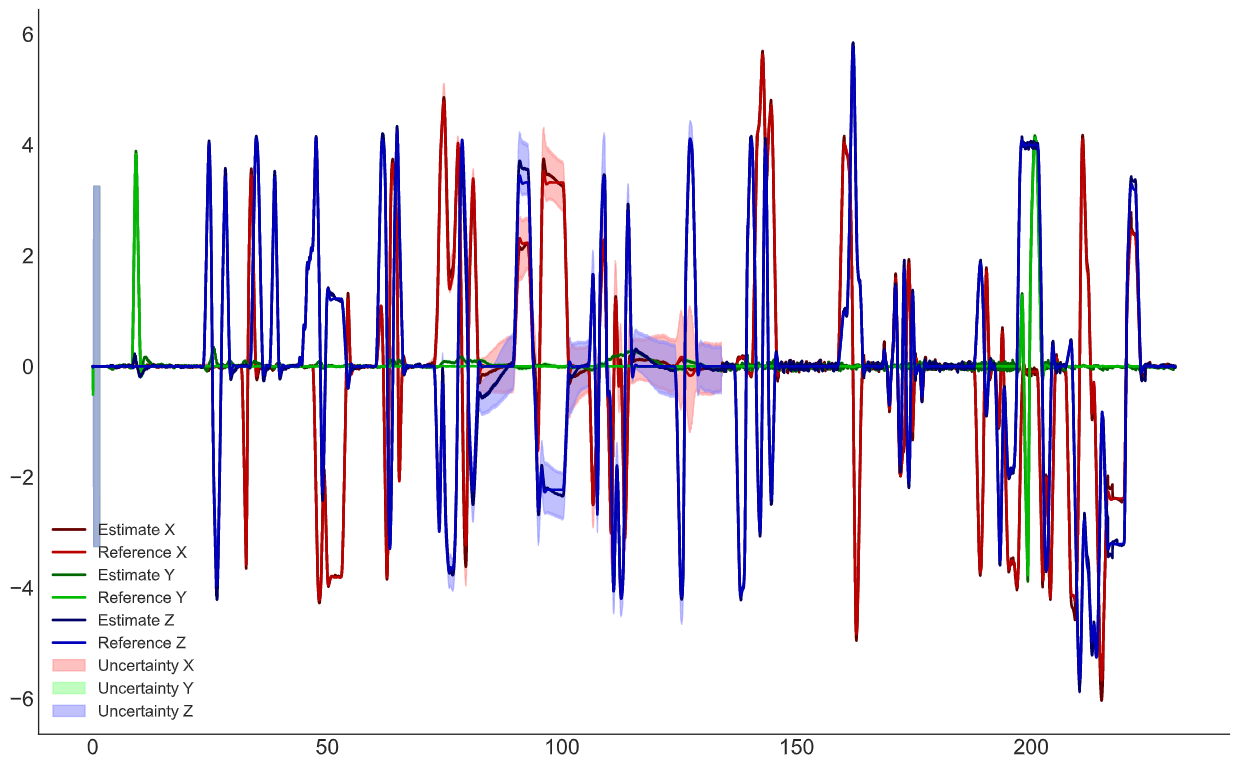 Вектор скоростей
Вектор скоростейПояснение по графикам: Estimate — это оценка ФК, Reference — это фактическая величина, Uncertainty — дисперсия из матрицы ковариации *100.
В центре графиком видно, что ошибка возросла, это произошло из-за уменьшения влияния GNSS данных (на видео видно, где я увеличил дисперсию GNSS corr).
Демку, что на видео можно скачать из репа:
Исходный код демки
А также можно поиграть интерактивно.
Можно заметить, что не использовался магнитометр для коррекции курса. Если применять обычный фильтр Magwick или Mahony тангаж и крен более менее наблюдаемы, когда нет линейных ускорений, то угол курса будет плыть и взять его неоткуда. А если постоянно присутствуют линейные, центростремительные ускорения, то все углы уплывут при коррекции акселерометром, это актуально для самолетов например.
В случае применения ФК и данной мат. модели, такого не будет, при наличии движения с помощью датчика GNSS будет происходить разделение сырого вектора ускорения из акселерометра на линейную часть и на вектор ускорения свободного падения, из-за чего углы тангажа и крена будут максимально точными, а угол курса не будет уплывать. К тому же мы получаем еще и более точный векторы положения и скорости. Данную особенность приметил, не только я:
В этом и заключается преимущество ФК — нахождении неявных полезных обратных зависимостей между вектором состояния и датчиками.
Вот график и видео иллюстрирующие коррекцию курсового угла, даже при начальном неправильном значении в 45 градусов.
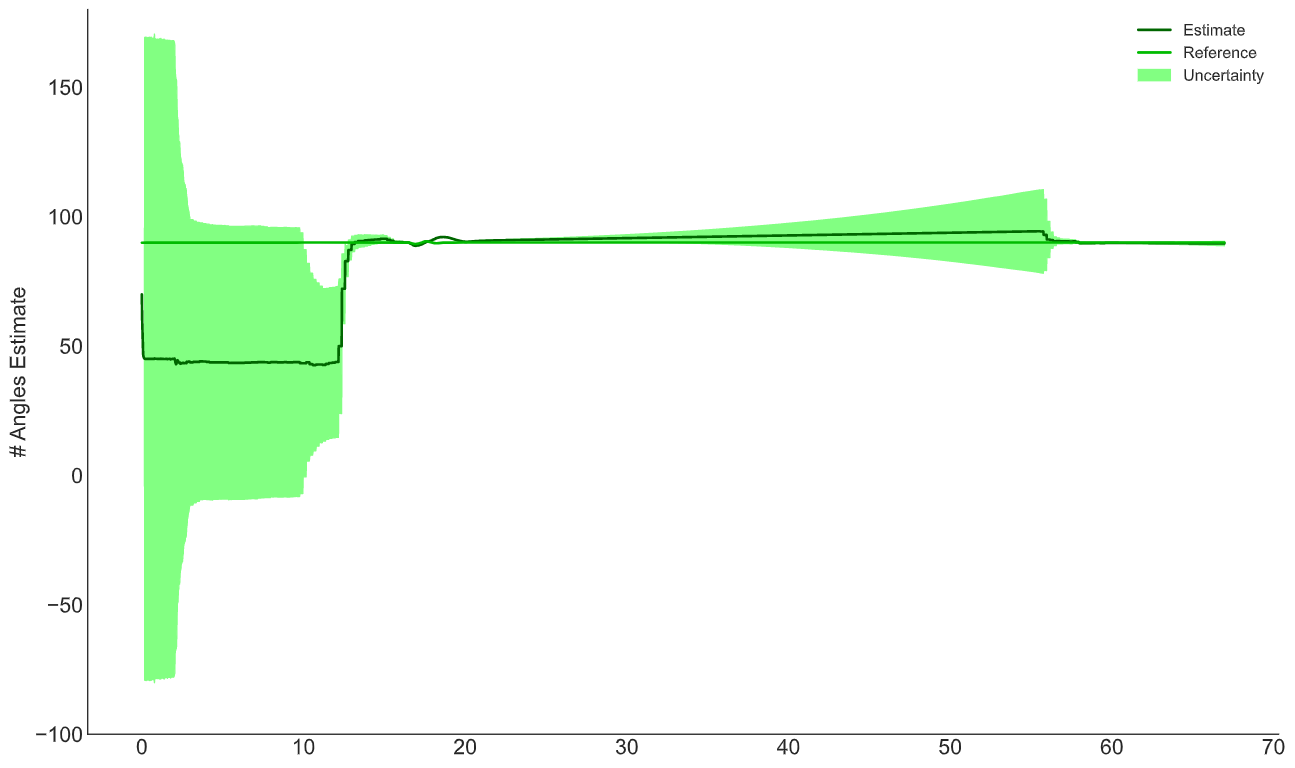 Угол курса с начальной ошибкой в 45 градусов
Угол курса с начальной ошибкой в 45 градусовВ интерактивной демке, много чего нет, с чем можно поиграть непосредственно в Unity Edior, а именно: различные значения bias IMU, их изменения во времени, различные величины стандартных отклонений шумов прогноза и датчика GNSS, задержки между датчиками, неверные начальные условия и т.д. Так что советую скачать исходник и непосредственно в Unity Editor поиграть с различными условиями.
Самое полезное, это то, что тот же самый C++ код, который работает в демке (kalman lib), можно целиком без переделок запустить на микроконтроллере, на реальном железе в реальных условиях.
Вот например коптер, который я собрал, который летает почти с таким же ФК:
Суть ФК можно расширить на оптимизацию не только текущего вектора состояния в конкретный момент времени, но и оптимизацию, например, целого набора состояний, включенных в разные моменты времени (Sliding-Window Optimization, bundle adjustment/graph optimization). Такой подход требует гораздо большей вычислительной мощности и реализуется другими методами, однако гораздо более точен и стабилен.
За рамками статьи остались такие темы, как:
моделирование других различных датчиков, например видеокамеры, лидаров, колесных одометров;
учет задержки в ФК между получением данных с различных датчиков;
применение параметров с ограничениями (вектора единичной длины, кватернионы) в ФК с высоко нелинейными моделями;
Регистрация некачественных данных с датчика на основе мат. модели;
Алгоритмы нелинейной оптимизации во временном окне (Sliding-Window Optimization)
Если вам будет интересно можно продолжить цикл статей по практическому применению ФК.
Список литературы:
Van Der Merwe, R. Sigma-point Kalman filters for probabilistic inference in dynamic state-space models
Chaabane, M. Nonlinear State and Parameter Estimation Using Iterated Sigma Point Kalman Filter: Comparative Studies
Christoph Hertzberga, Integrating Generic Sensor Fusion Algorithms with Sound State Representations through Encapsulation of Manifolds
Joan Sol`, Quaternion kinematics for the error-state Kalman filter
