Факторное моделирование с помощью нейронной сети12.10.2016 18:18

Введение. Классический факторный анализ [1] позволяет на базе выборки различных показателей сформировать факторные показатели с необходимой точностью описывающие исходный объект и уменьшающие размерность задачи путем перехода к ним. Факторные показатели являются линейной комбинацией исходных показателей. Тем самым факторные модели носят линейный характер.

Нейронная сеть позволяет аппроксимировать отображения между исходными и целевыми показателями. При этом аппроксимируемые отображения могут иметь нелинейный характер. Двухслойный персептрон позволяет аппроксимировать любую булеву функцию булевых переменных [2]. Двухуровневая нейронная сеть способна аппроксимировать в равномерной метрике с любой заданной погрешностью ε> 0 любую непрерывную функцию , а в среднеквадратической метрике — любую измеримую функцию, определенную на ограниченном множестве [3, 4, 5, 6].

Для восстановлений закономерностей между параметрами используется специальный алгоритм обучения нейронной сети: алгоритм обратного распространения ошибки [7]. Этот алгоритм с математической точки зрения представляет собой градиентный метод оптимизации.

Суть данного метода для построений факторных моделей заключается в том, что для выявления закономерностей между параметрами используется математическая модель нейронной сети с линейной передаточной функцией. Значения факторных переменных определяется равным значениям выходных сигналов нейронов скрытого слоя нейронной сети. Тем самым нейронная сеть осуществляет классический факторный анализ, т.е. строит линейные комбинации исходных параметров [8, 9, 10].

В данной работе предлагается усовершенствованный алгоритм обратного распространения ошибки посредством введения дополнительного слагаемого в функцию ошибки для построения интерпретируемой факторной структуры и решения задачи факторного вращения на базе нейронной сети.

Математическая модель нейрона.Состояние нейрона описывается набором переменных:

весами входных сигналов 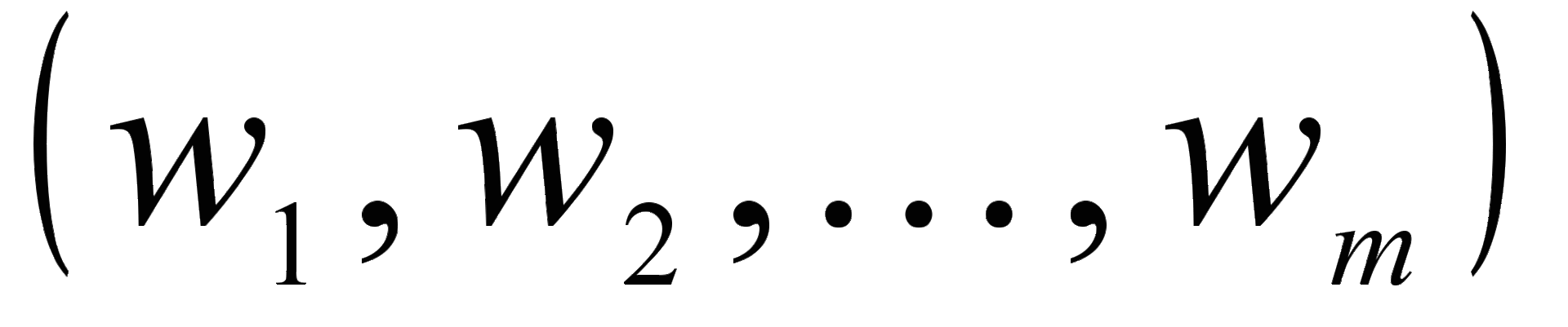, где m— количество входных сигналов ;

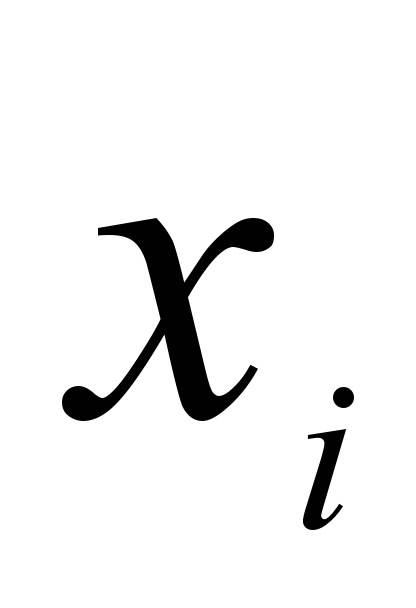свободным членом 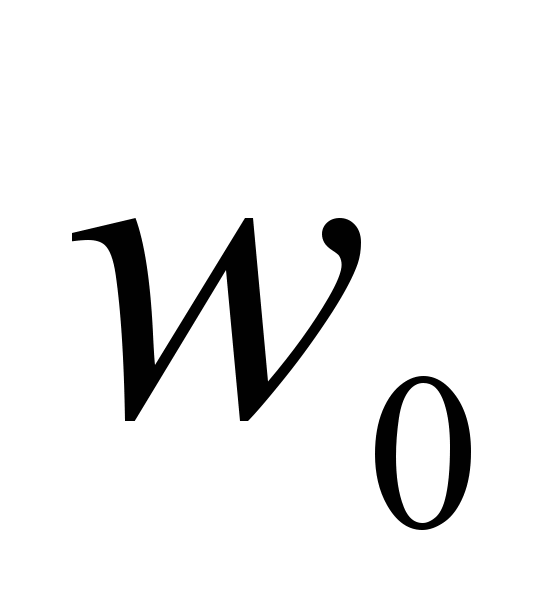в вычислении выходного сигнала. Сигнал на выходе нейрона вычисляется по формуле:

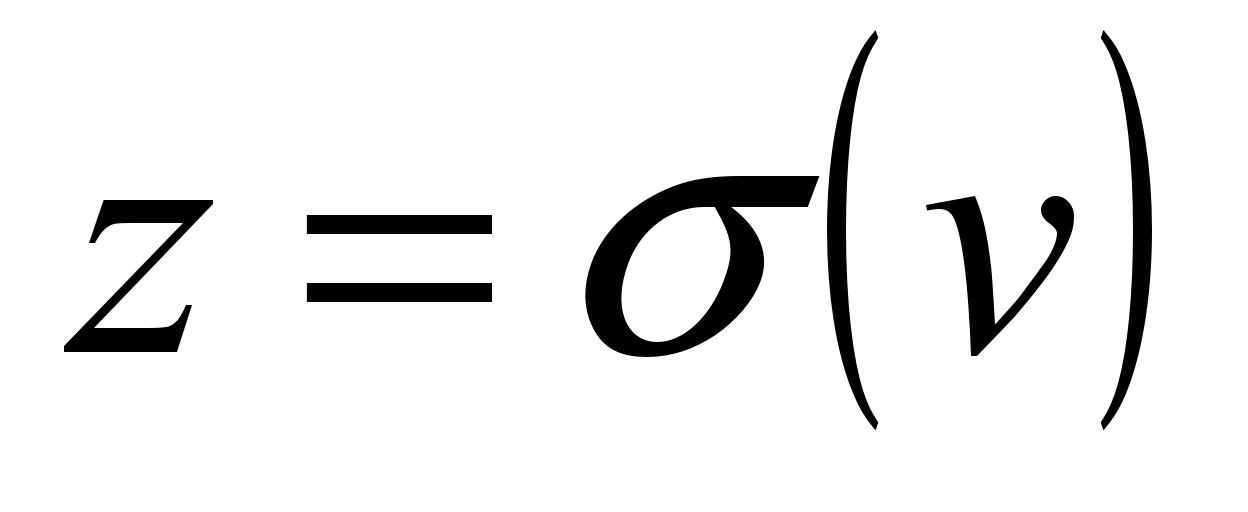, где 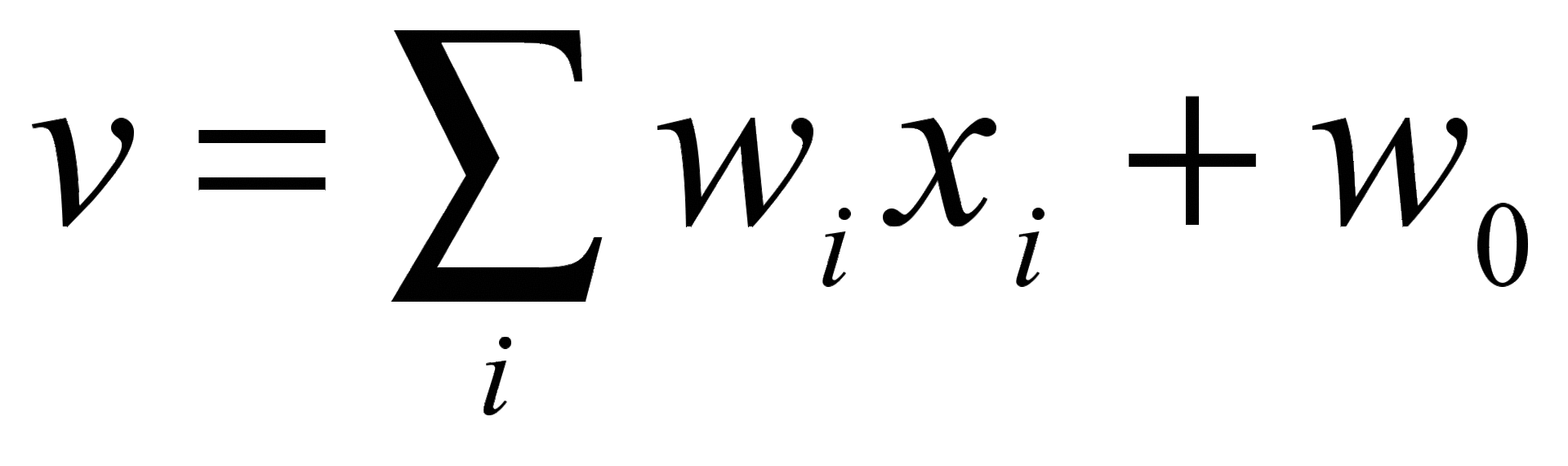— взвешенная сумма сигналов на входах нейрона,

σ — передаточная функция нейрона, например сигмоидальная функция .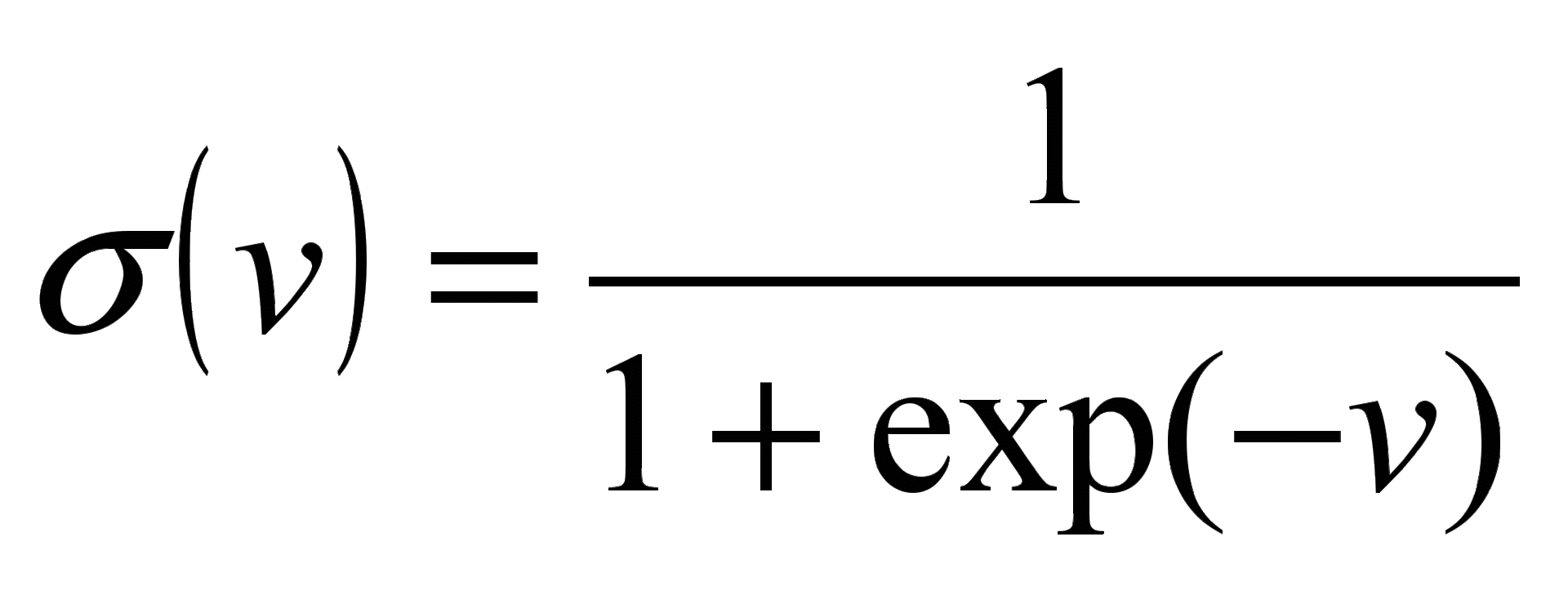

Нейронная сеть. Отдельные нейроны объединяются в слои. Выходные сигналы нейронов из одного слоя поступают на вход нейронам следующего слоя, модель так называемого многослойного персептрона (рис. 1). В программной реализации авторской нейронной сети вводится понятие нейронов потомков и нейронов предков. Все нейроны, имеющие входной сигнал от данного нейрона являются его потомками или пассивными нейронами или аксонами. Все нейроны образующие входные сигналы данного нейрона являются его предками или активными нейронами или дендритами.

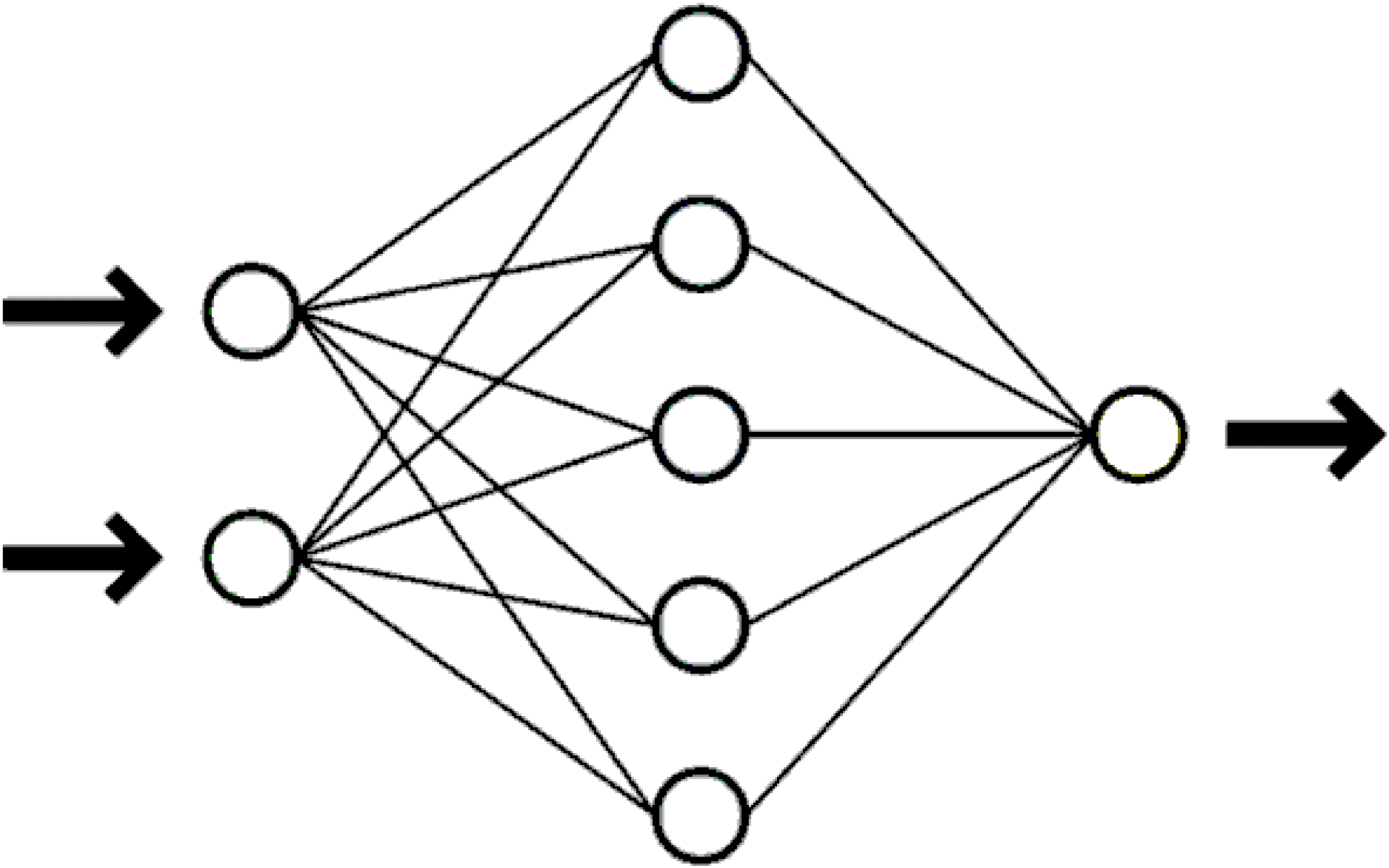
Рис. 1.Схема простой нейронной сети (входные нейроны, скрытые нейроны, выходной нейрон).

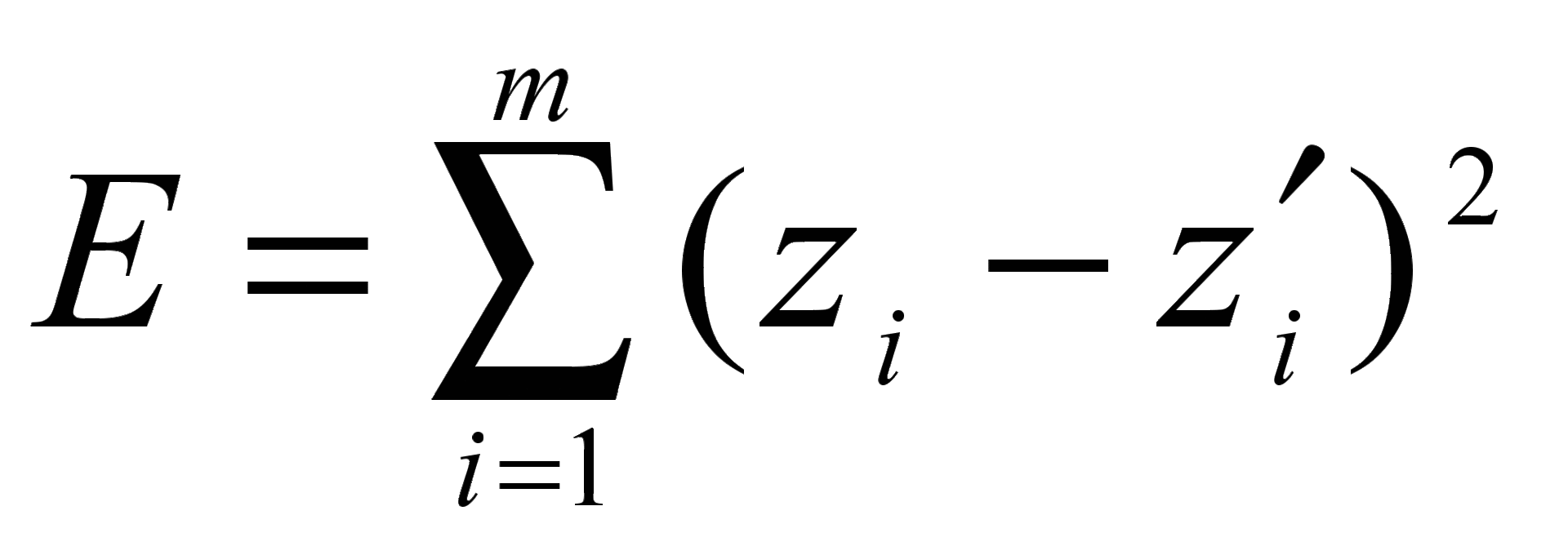
Алгоритм обратного распространения ошибки. Алгоритм обратного распространения ошибки для обучения нейронной сети соответствует минимизации функции ошибки E(wij). В качестве такой функции ошибки может быть использована сумма квадратов отклонений выходных сигналов сети от требуемых:

,

где − выходное значение i-го нейрона выходного слоя,

− требуемое значение i-го нейрона выходного слоя.

В данном алгоритме итерация обучения состоит из трех процедур:

1. Распространение сигнала и вычисление сигналов на выходе каждого нейрона.

   
   

2. Вычисление ошибки для каждого нейрона.

   
   

3. Изменение весов связей.

   
   

Путем многократного цикличного подставления наборов сигналов на входе и выходе и обратного распространения ошибки производится обучение нейронной сети. Для многослойного персептрона и определенного вида передаточной функции нейрона, при определенном виде функции ошибки доказана сходимость этого метода [11].

Вычисление ошибок. Если передаточная функция нейронов является сигмоидальной, то ошибки для нейронов различных слоев вычисляются по следующим формулам.

Вычисления ошибок для нейронов выходного слоя производится по формуле:

,

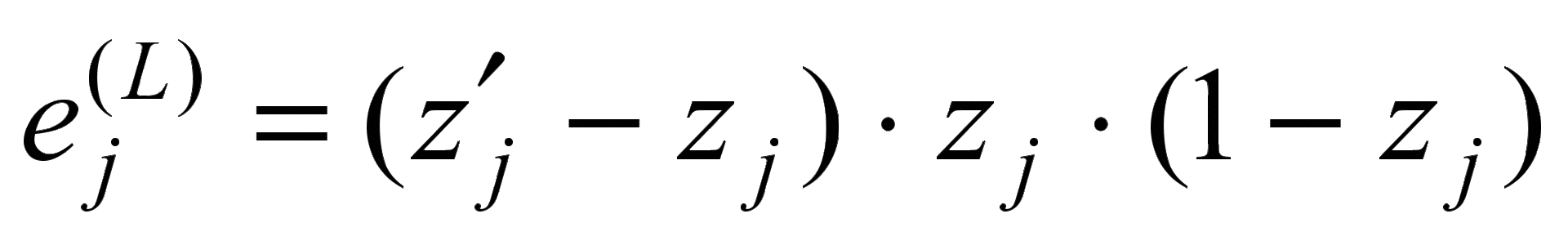где — желаемое значение на выходе j-го нейрона выходного слоя L,

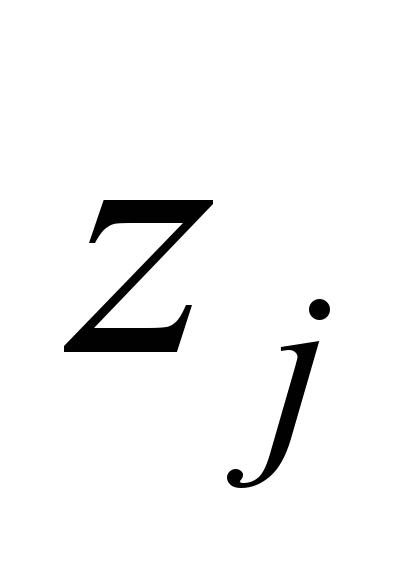— сигнал на выходе j-го нейрона выходного слоя L,

L— глубина нейронной сети,

Ошибки для нейронов остальных слоев рассчитываются по формуле:

,

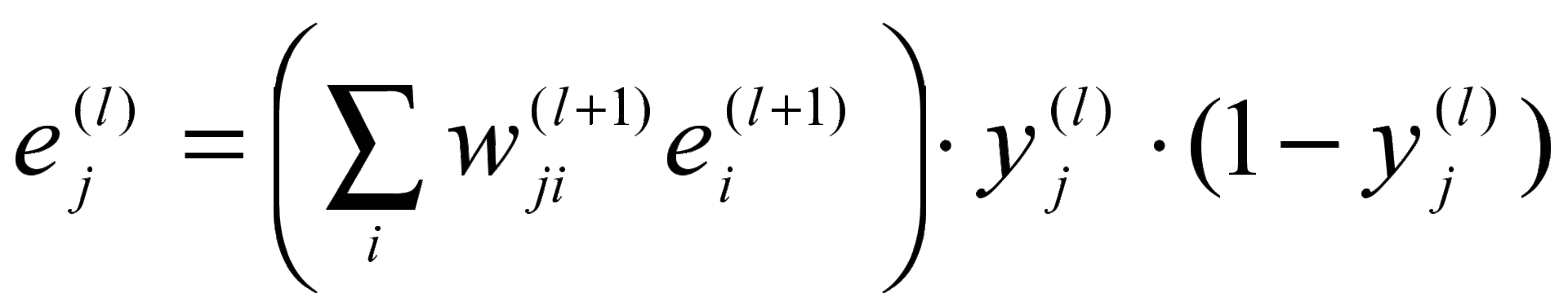где i— индексы нейронов-потомков данного нейрона,

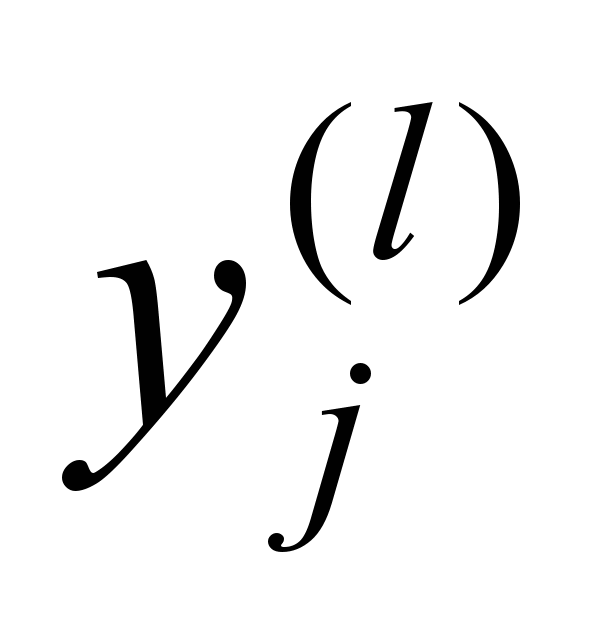— сигнал на выходе j-го нейрона слоя l,

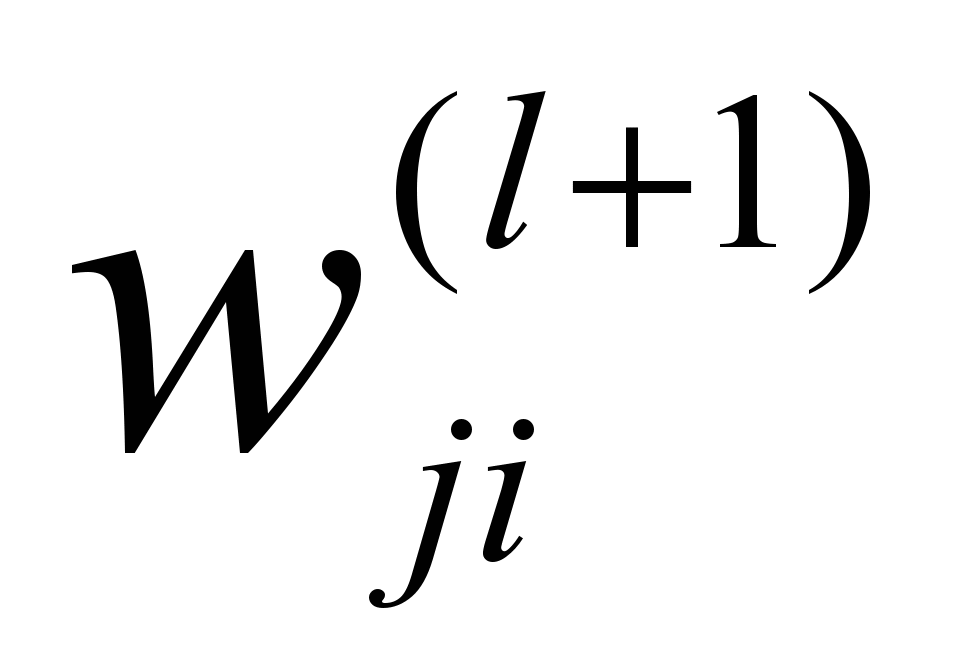— связь междуj-ым нейроном l-го слоя и i-ым нейроном (l+1)-го слоя.

Изменение пороговых уровней нейронов и весов связей. Для изменения весов связей используется следующая формула:

,

,

,

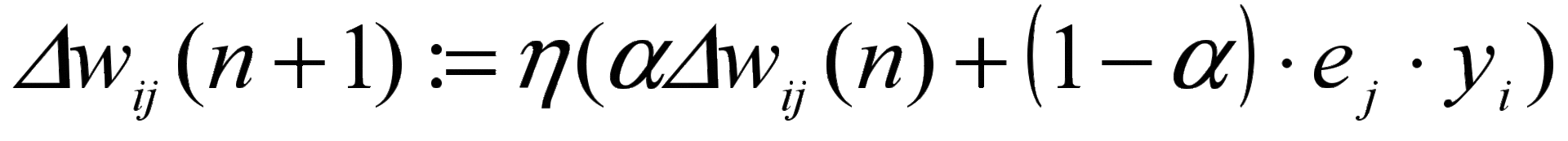
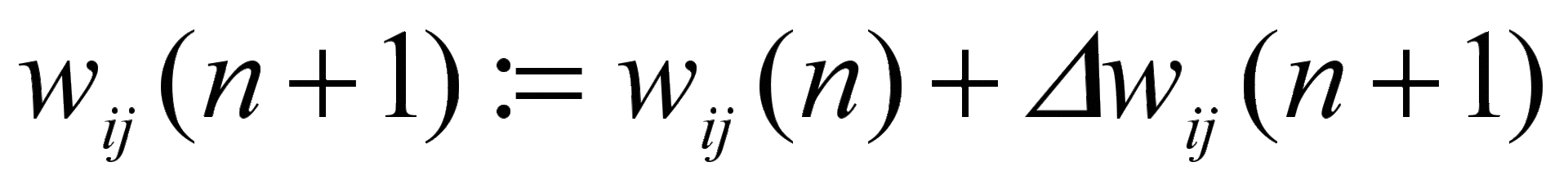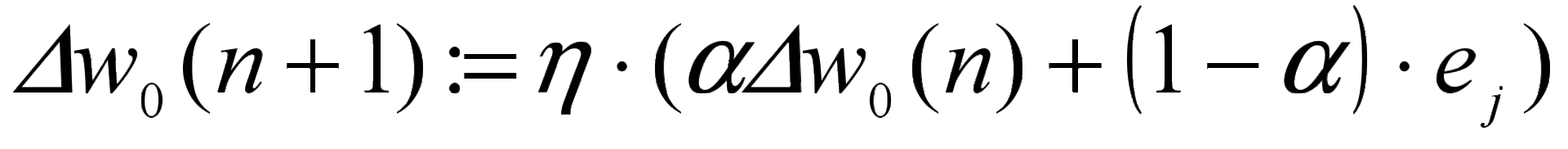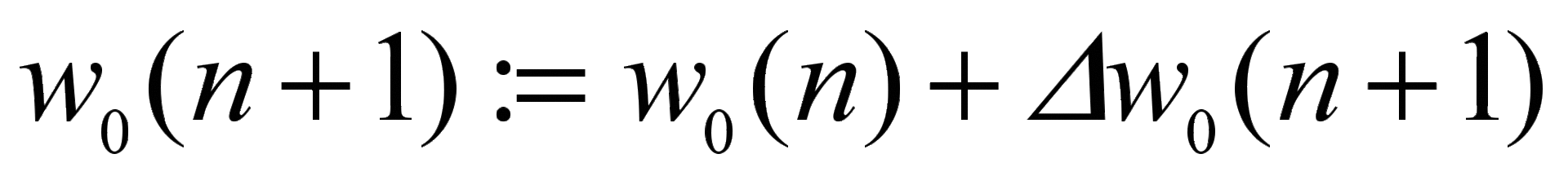где i— индекс активного нейрона (нейрона источника входных сигналов пассивных нейронов),

j— индекс пассивного нейрона,

n–номер итерации обучения,

α— коэффициент инерциальности для сглаживания резких скачков при перемещении по поверхности целевой функции,

0<η<1— множитель, задающий скорость «движения».

Метод построения факторной модели. Факторный анализ основывается на следующей линейной модели, связывающей исходные показателии факторы :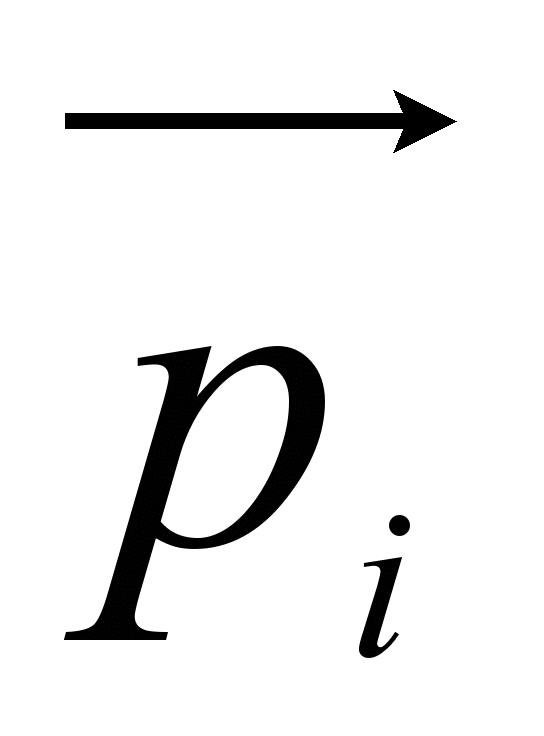

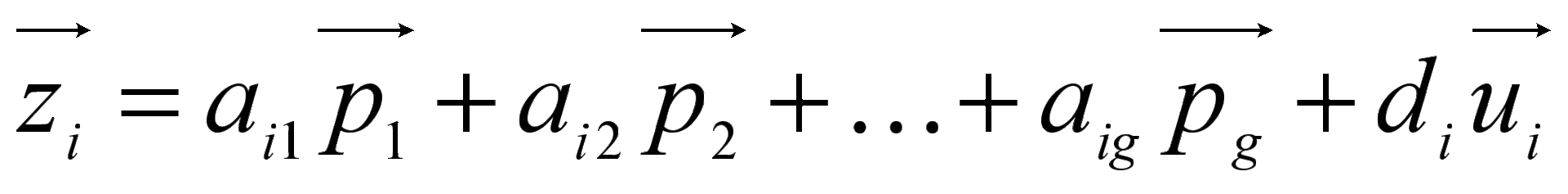
m— число переменных,

g— число факторов,

− исходные переменные,

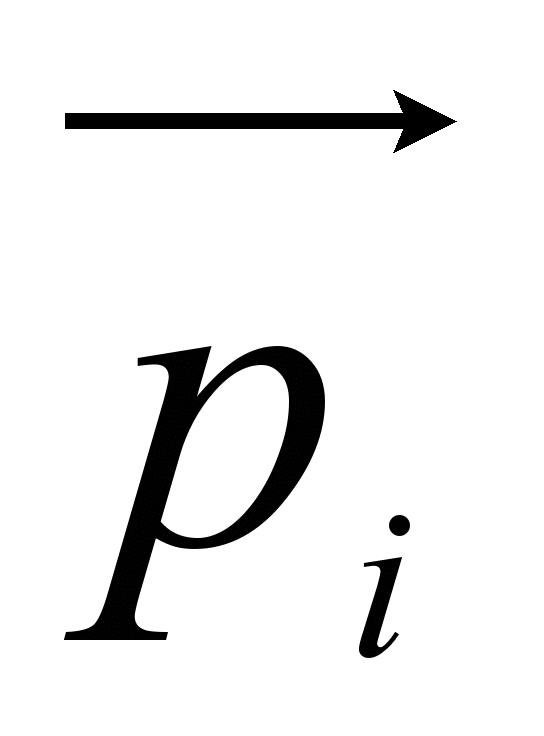− общие факторы,

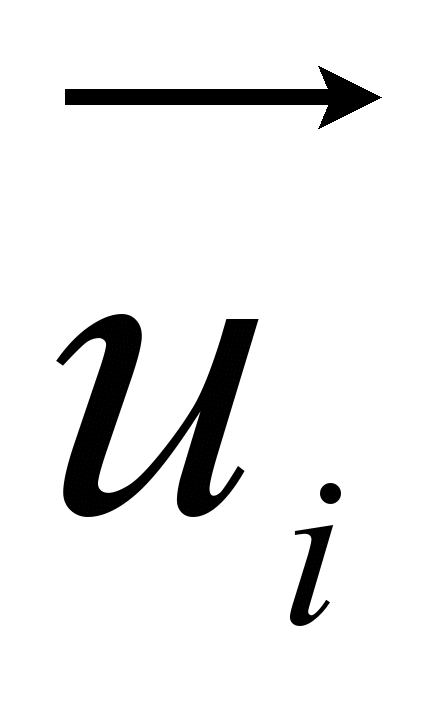− специфичные факторы.

В матричном виде линейная модель факторного анализа записывается в виде:

,

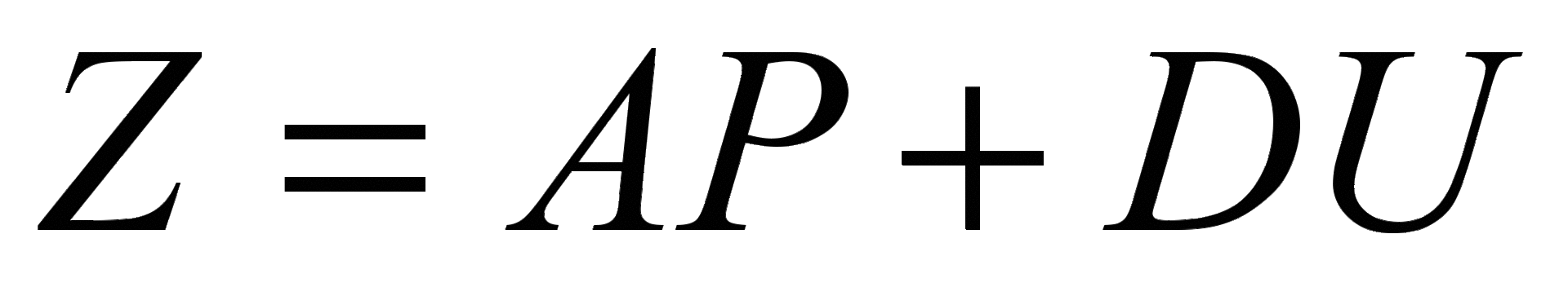где 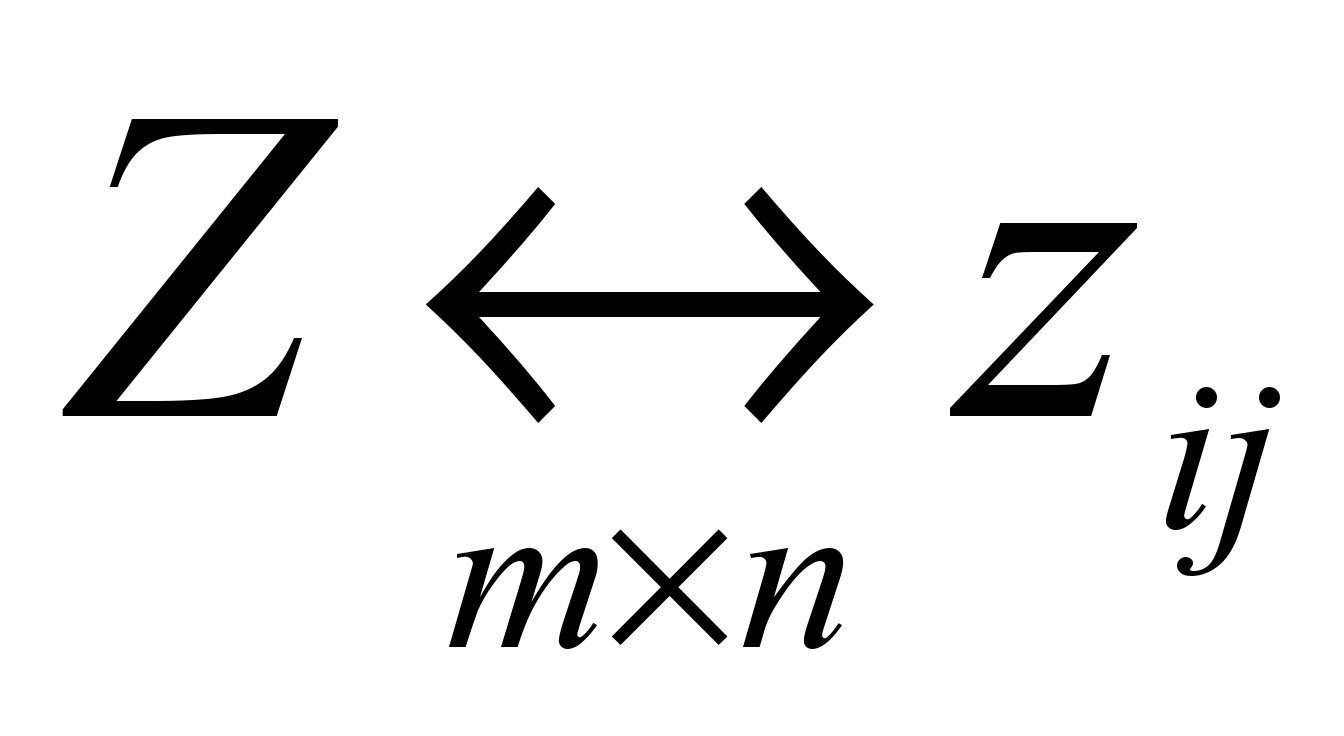− матрица размерности 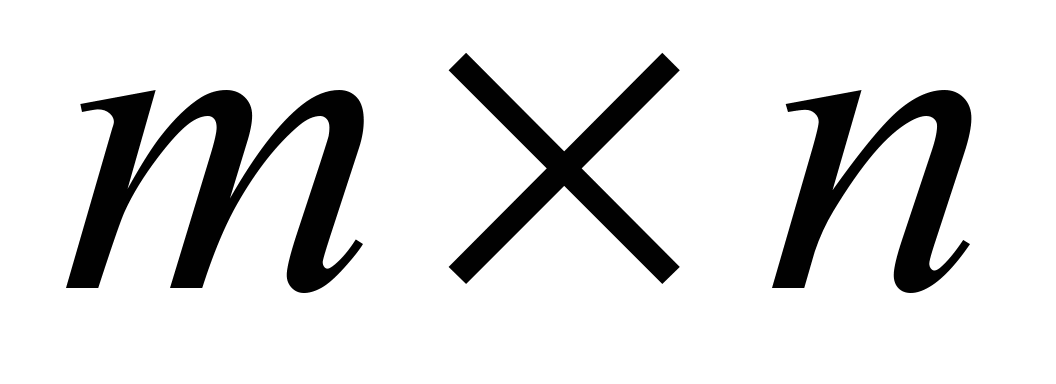значений mпараметров у nобъектов,

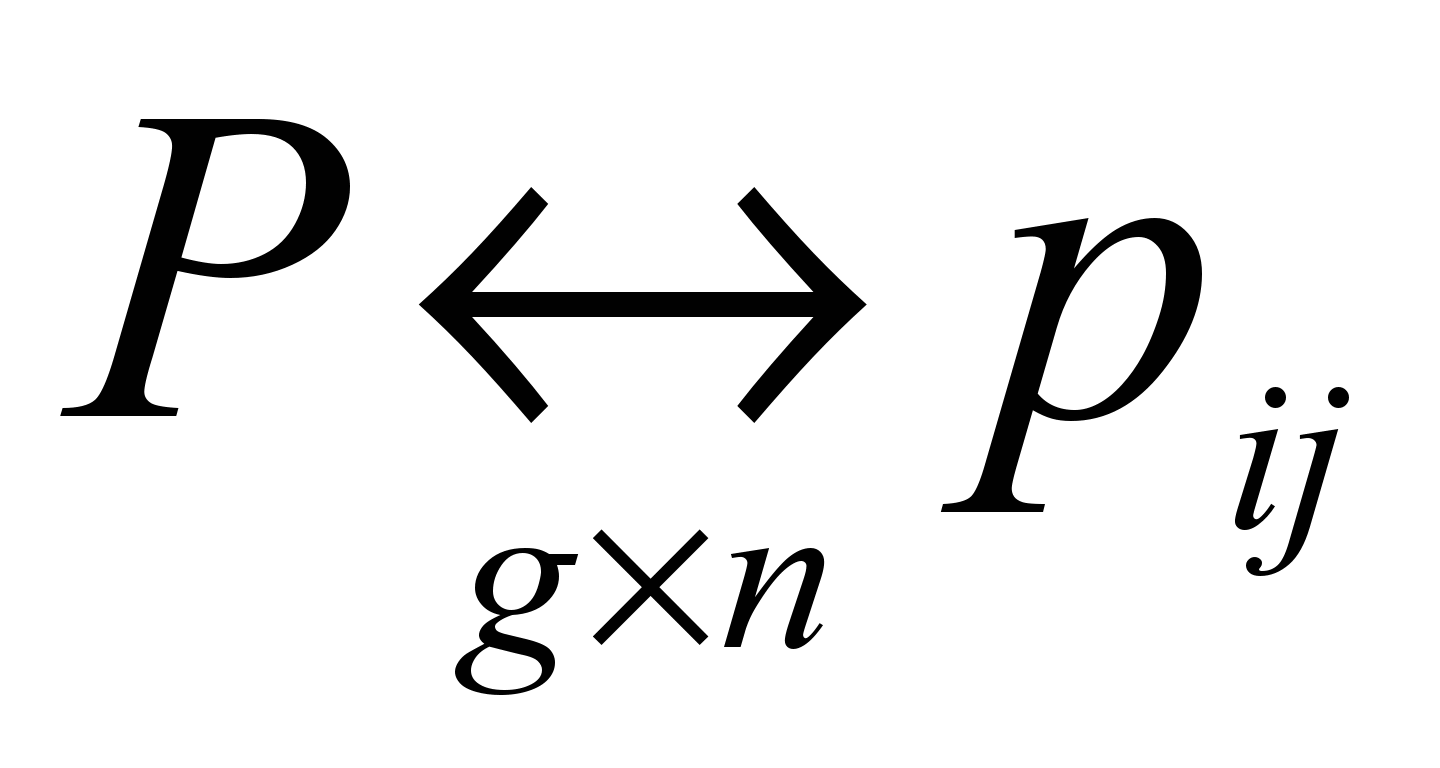− матрица размерности 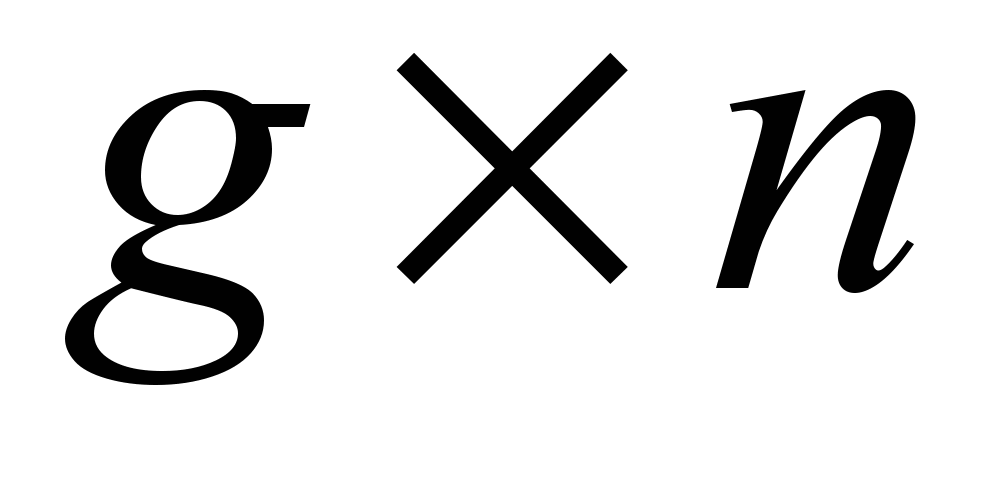значений g факторов у nобъектов,

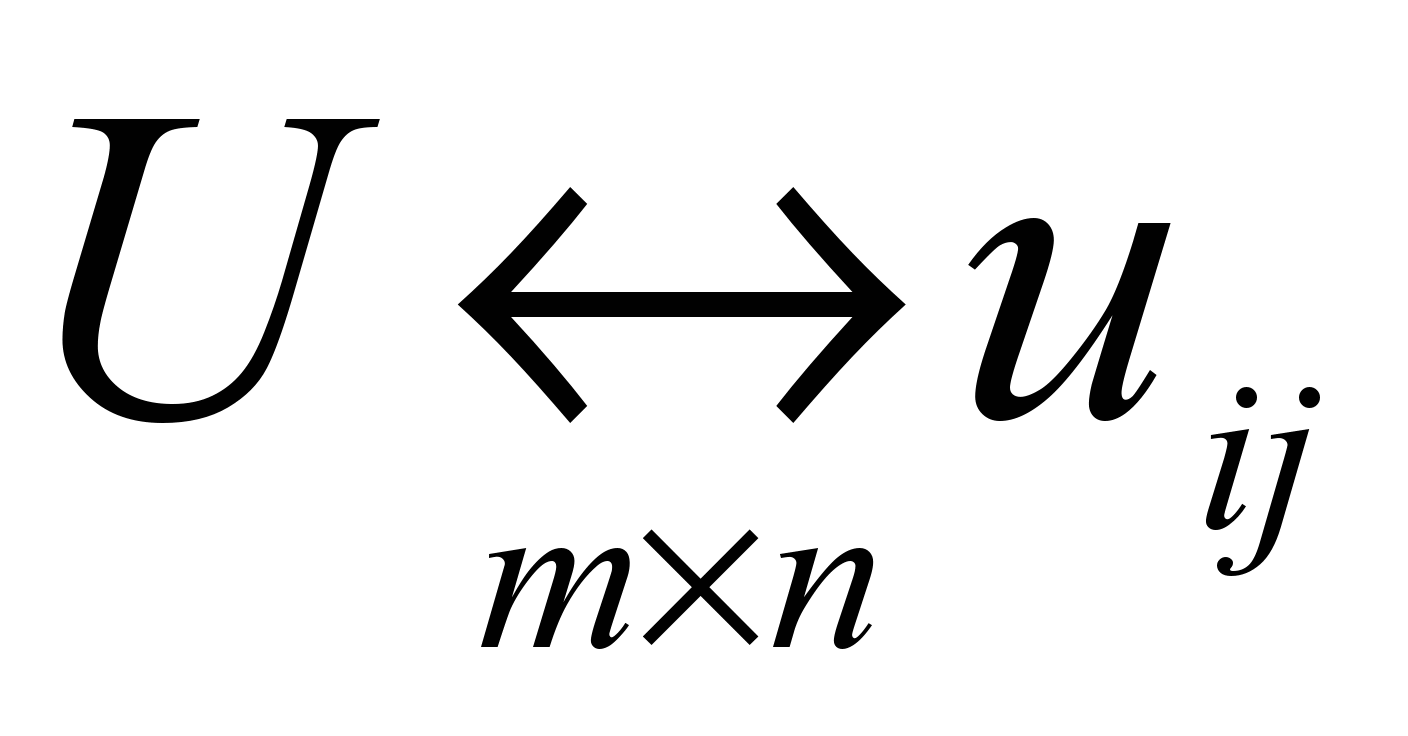− матрица размерности 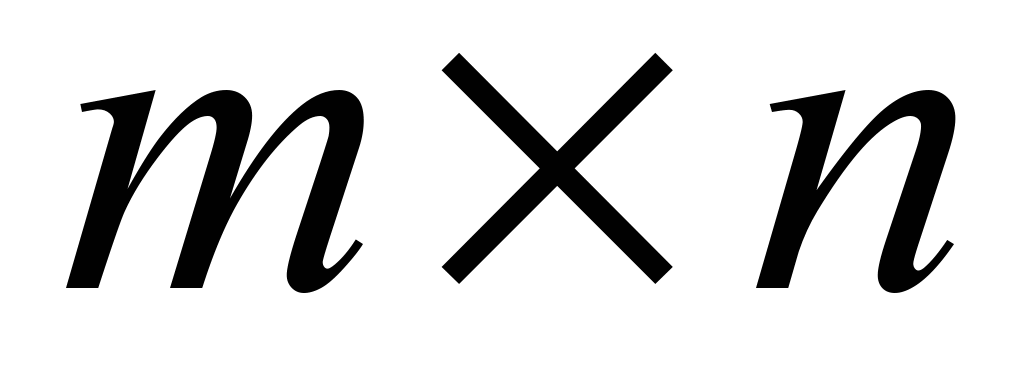значений mспецифичных факторов у nобъектов,

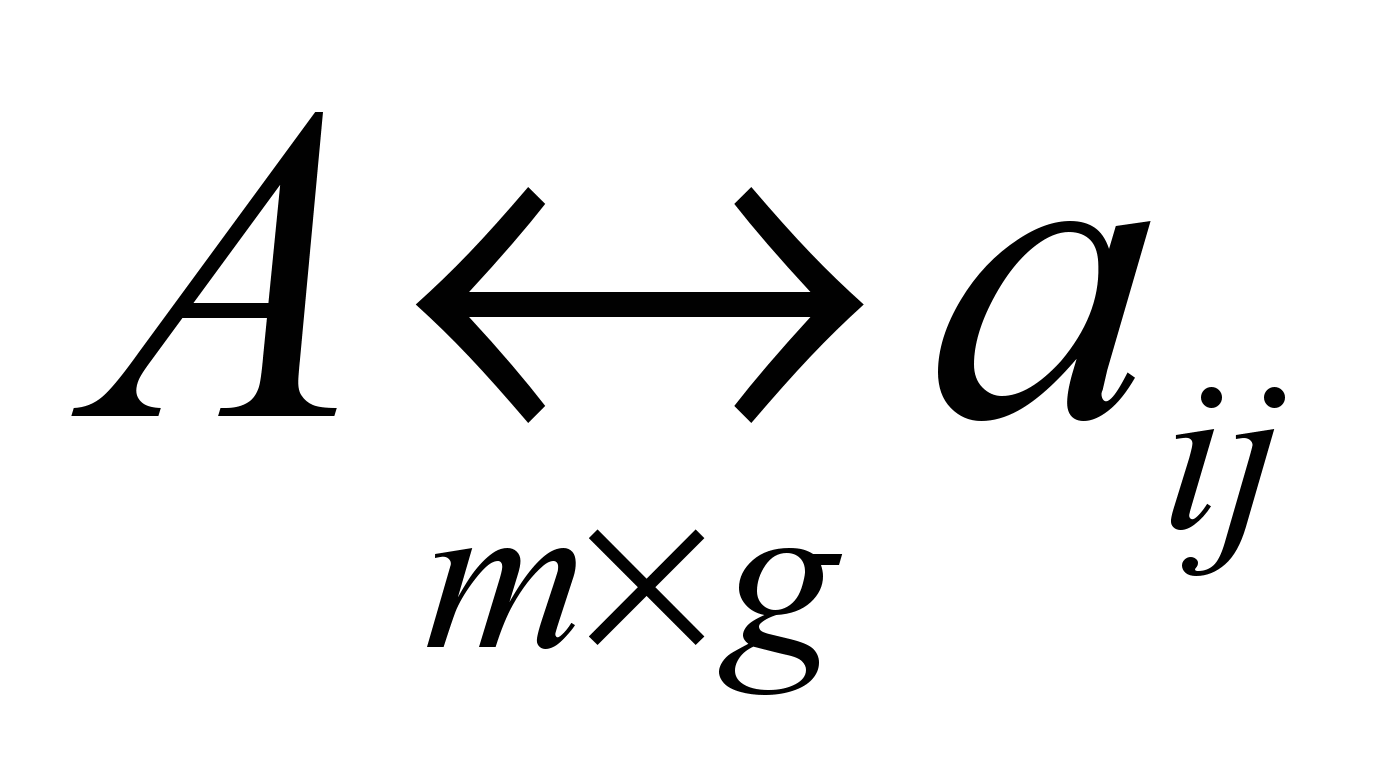− матрица факторного отображения размерности 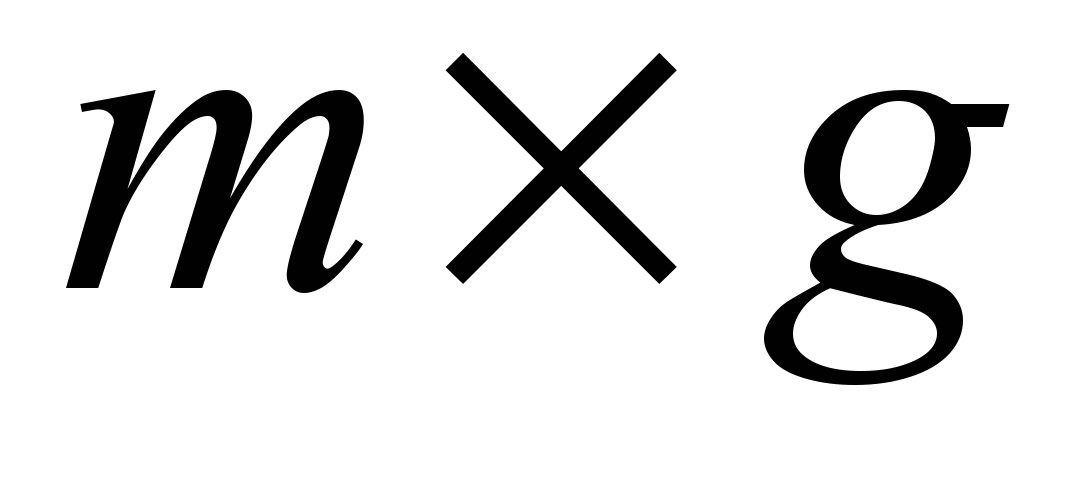весовых коэффициентов,

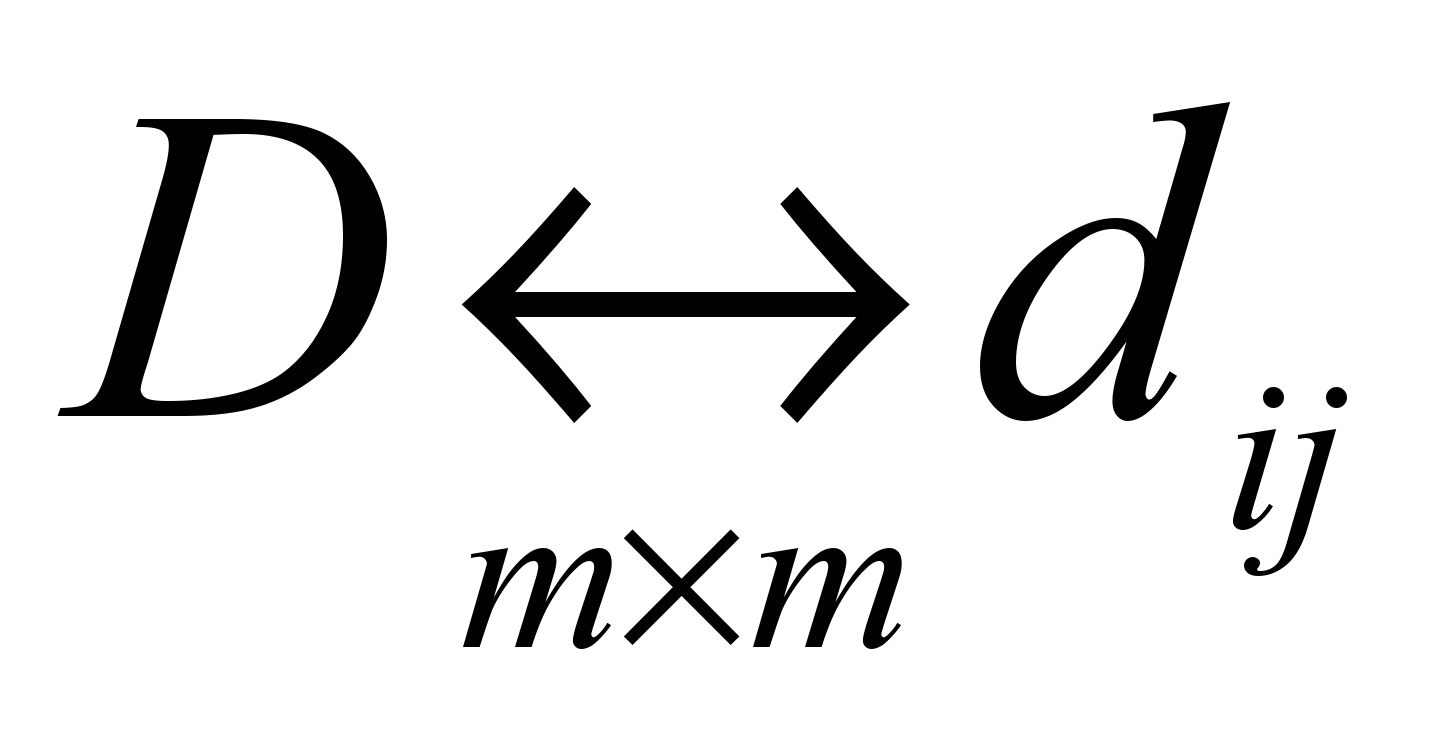− диагональная матрица размерностивесовых коэффициентов специфичных факторов.

В данном методе построения факторной модели латентные характеристики ставятся в соответствие нейронам скрытого слоя. При этом число нейронов скрытого слоя полагают меньшим числа нейронов входного слоя для осуществления факторного сжатия входной информации. Для оценки числа нейронов скрытого слоя можно применять правило Кайзера классического факторного анализа. Нейронам входного и выходного слоя ставится в соответствие исходные характеристики объектов исследования. Когда передаточная функция нейронов линейна такая конфигурация нейронной сети соответствует классическому факторному анализу (рис. 2).

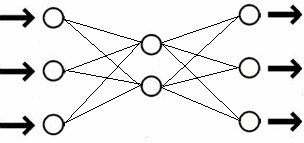
Рис. 2.Схема нейронной сети классического факторного анализа (число нейронов входного слоя равно числу нейронов выходного слоя, число нейронов скрытого слоя меньше числа нейронов входного слоя).

С помощью обучения нейронной сети вычисляются веса входных связей нейронов скрытого и выходного слоя, которые соответствуют элементам обратного и прямого факторного отображения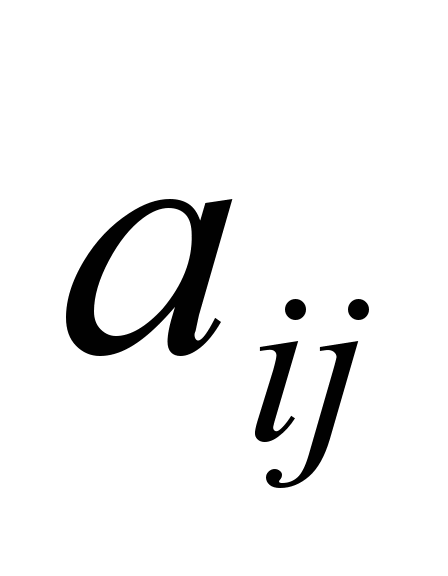. Веса нейронов ищутся в интервале [-1, 1]. Наполнение факторов исходными переменными определяется с помощью значений элементов факторного отображения и выбранного порогового уровня значимости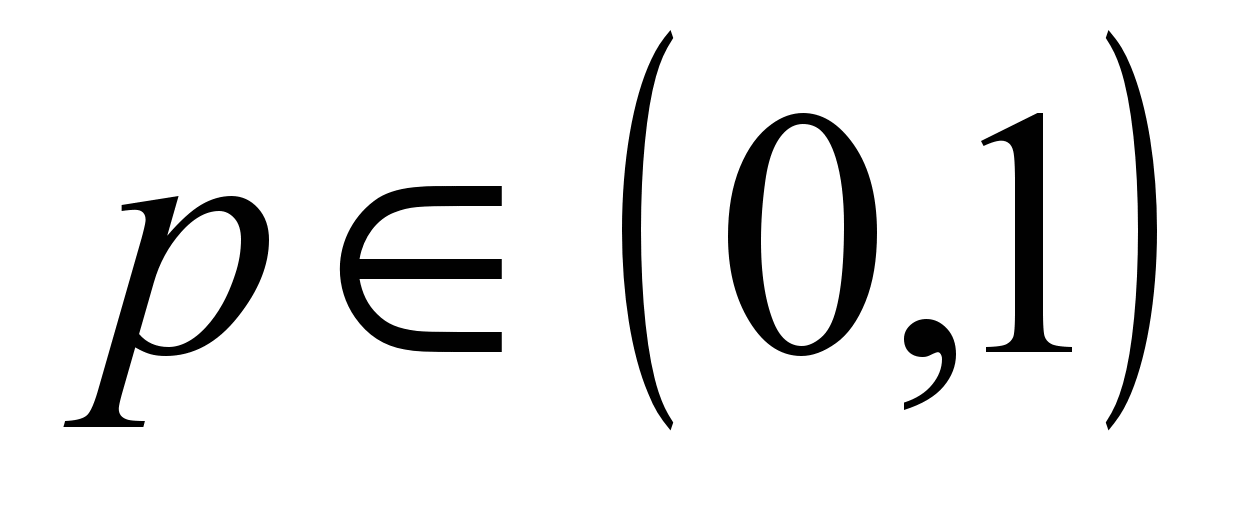. Переменная iвходит в фактор j, если .

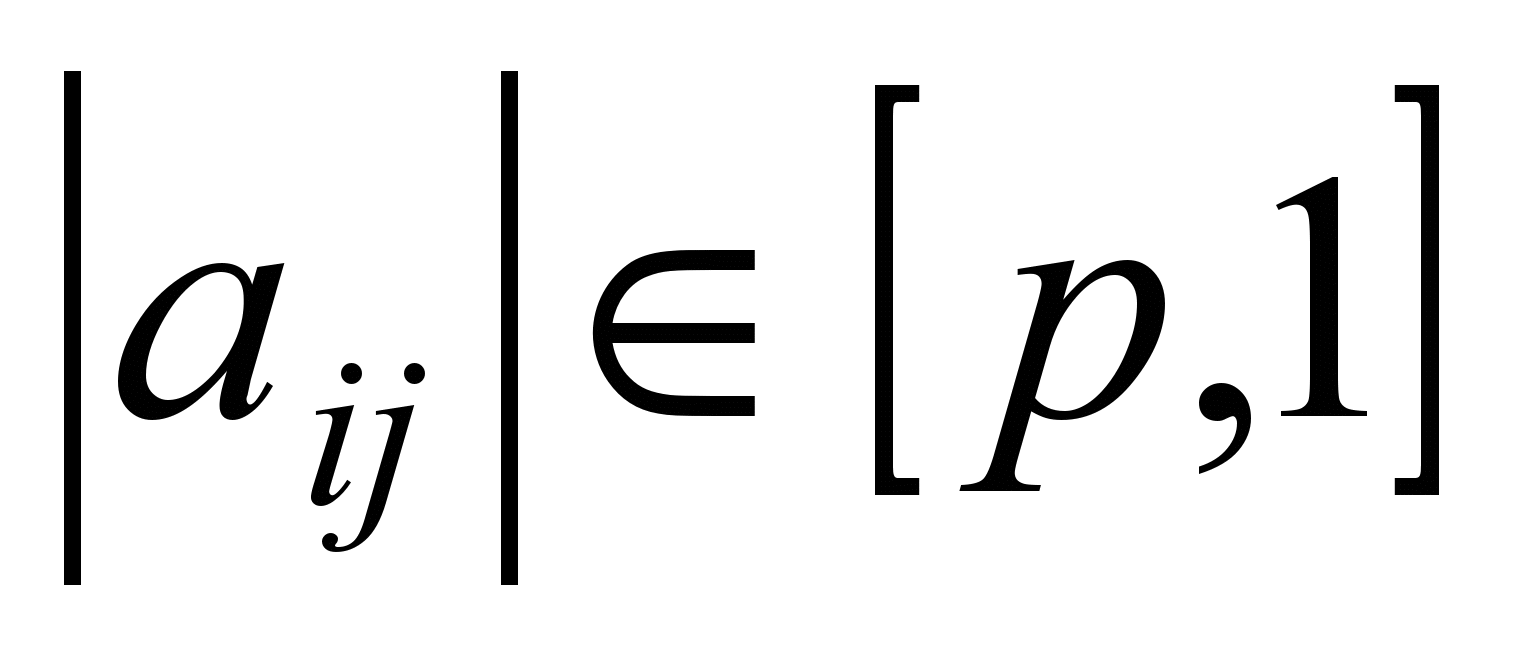Для раскрытия взаимосвязи факторной модели и нейронной сети, воспользуемся формулами получения выходного сигнала нейронов скрытого слоя.

Обозначим выходной сигнал j-го нейрона скрытого слоя 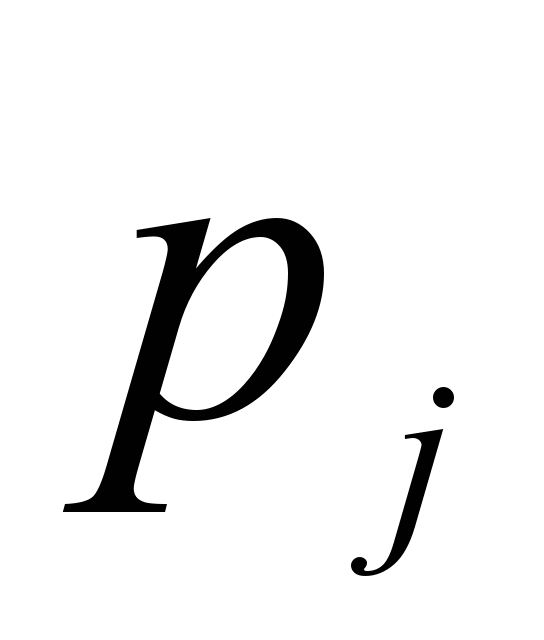. Выходной сигнал i-го нейрона входного слоя обозначим . В качестве передаточной функции будем использовать линейную функцию .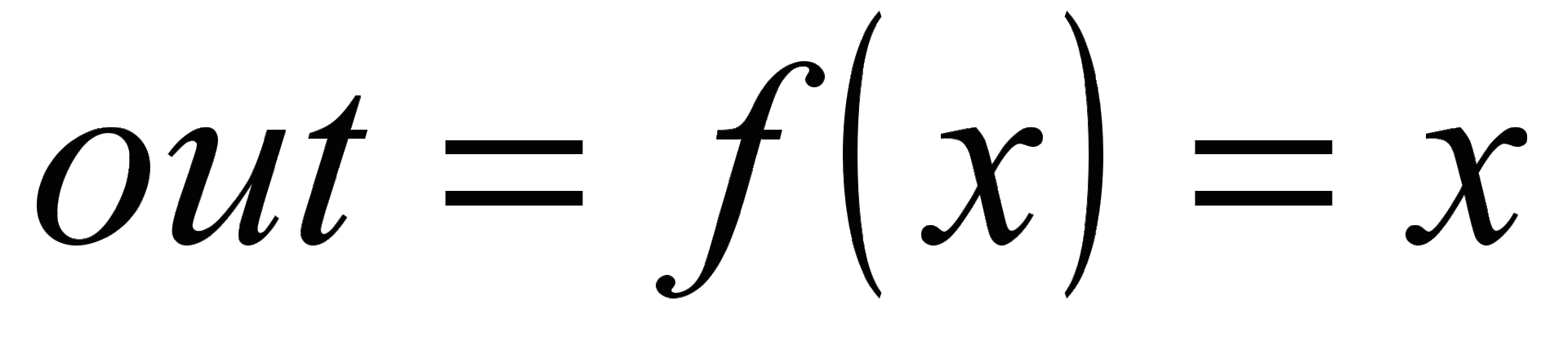

В результате

,

где m— число нейронов входного слоя;

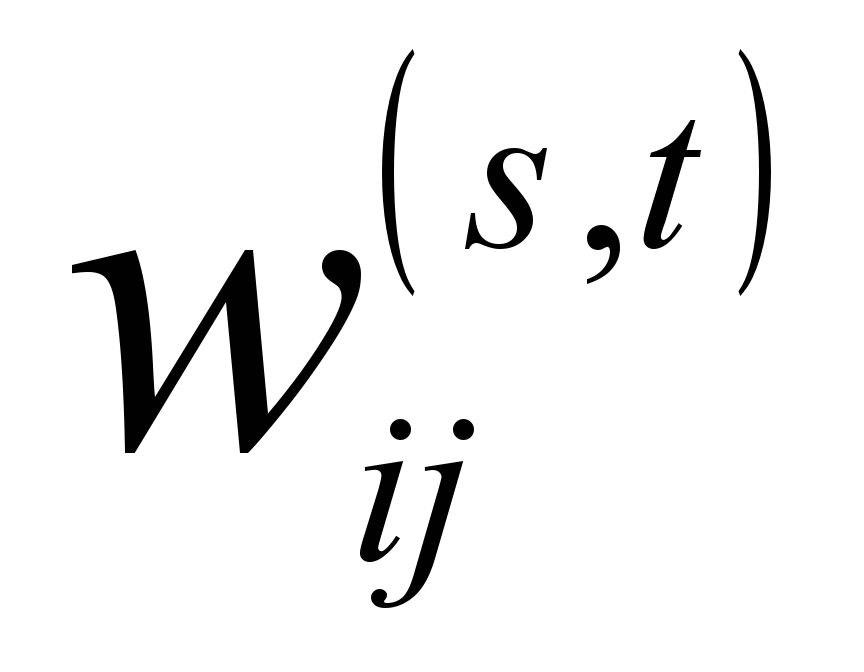− связь между i-ым нейроном s-го слоя и j-ым нейроном t-го слоя,

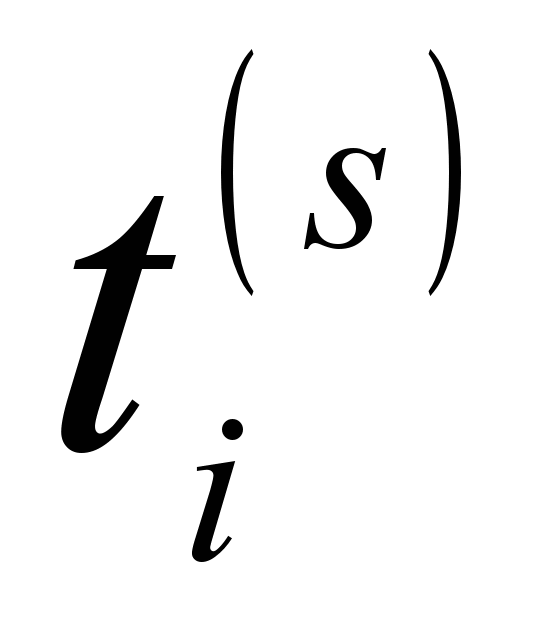− пороговый уровень i-го нейрона s-го слоя.

Аналогично для выходного слоя:

,

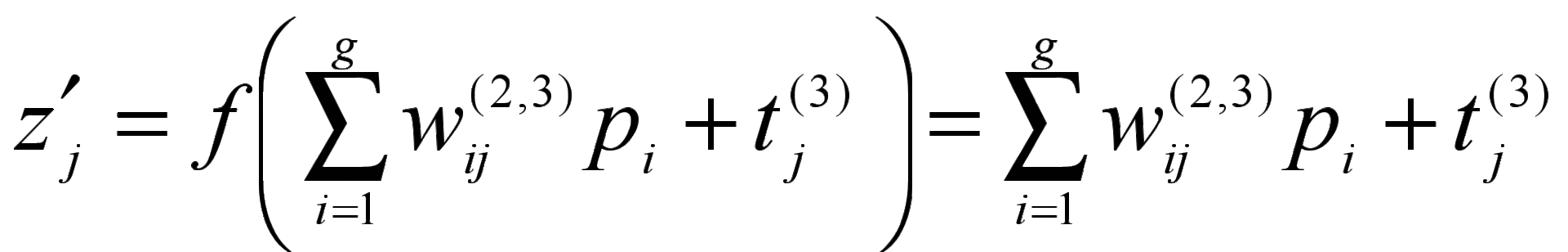где− выходное значение i-го нейрона выходного слоя,

g − число нейронов скрытого слоя.

Полученная линейная взаимосвязь переменных соответствует классической модели факторного анализа, в которой факторы являются линейными комбинациями исходных переменных. Задача поиска факторного отображения и значений факторов сводится к задаче поиска весов связей и пороговых уровней нейронной сети. Поскольку факторное отображение и значения факторов являются неизвестными, необходима сеть с промежуточным слоем. Сеть в целом осуществляет тождественное преобразование, т.е. выходной сигнал наi-ом нейроне входного слоя равен выходному сигналу i-го нейрона выходного слоя. Отдельные части сети (входная и выходная часть) соответствуют прямому и обратному факторному отображению.

Теорема.

Пусть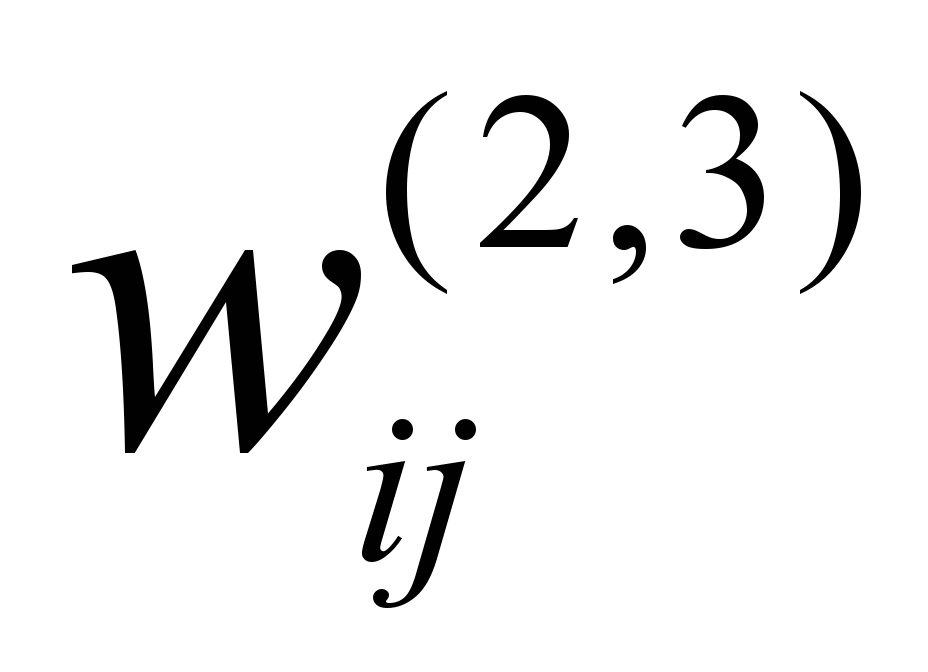и 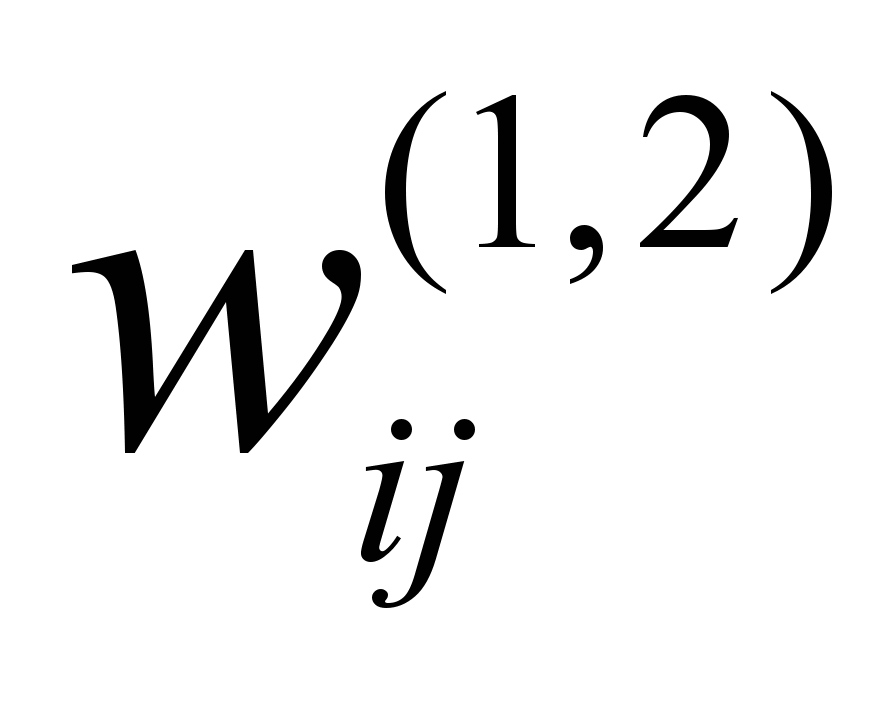− веса входных сигналов выходного и скрытого слоя нейронной сети с линейной передаточной функцией. Число нейронов на выходном слое равно числу нейронов входного слоя. Нейронная сеть состоит из входного, скрытого и выходного слоя и осуществляет тождественное преобразование для любого входного сигнала (вектор входных сигналов сети равен вектору выходных сигналов).

Тогда выполняется следующее равенство:

,

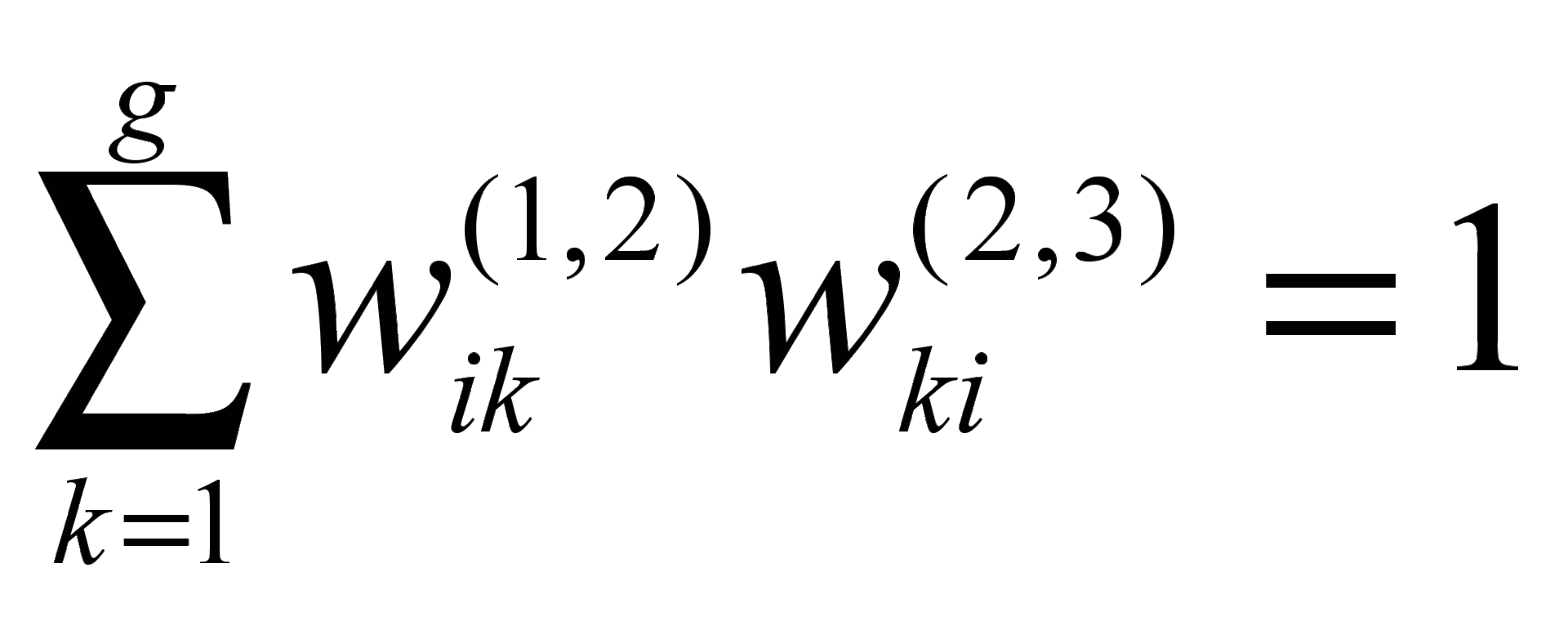где— связь междуi-ым нейрономs-го слоя иj-ым нейрономt-го слоя,

g − число нейронов скрытого слоя.

Доказательство:

Обозначим 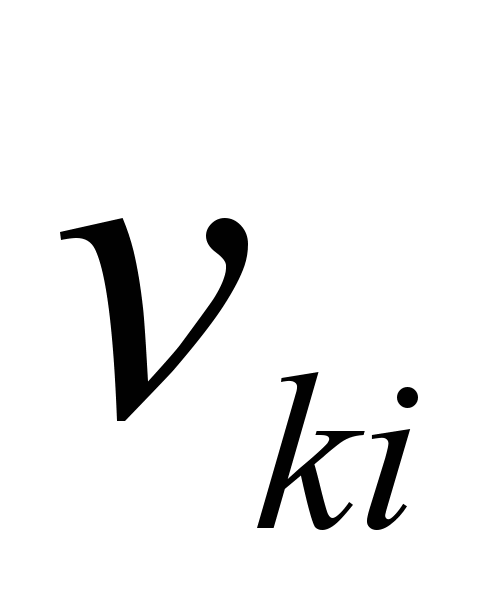— выходной сигнал i-го нейрона k-го слоя,

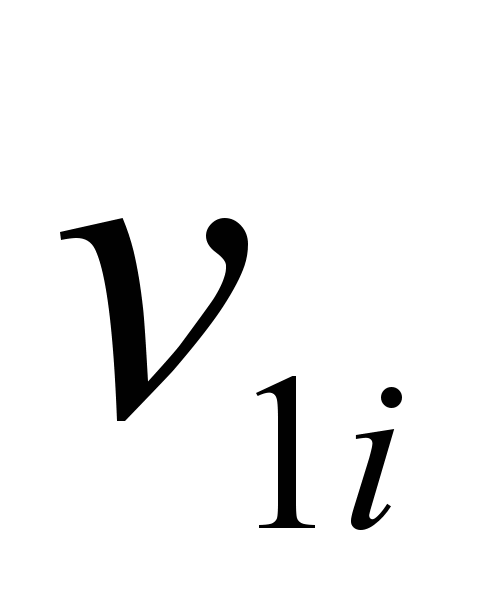— i-ый выходной сигнал нейронов первого слоя.

Для поиска весов нейронной сети необходимо выполнение условия:

, выходной сигнал на i-ом нейроне входного слоя равен выходному сигналу i-го нейрона выходного слоя. Из этого условия следует вспомогательное условие:

, изменение i-го входного сигнала сети равно изменениюi-го выходного сигнала. При этом справедливы следующие равенства:

,

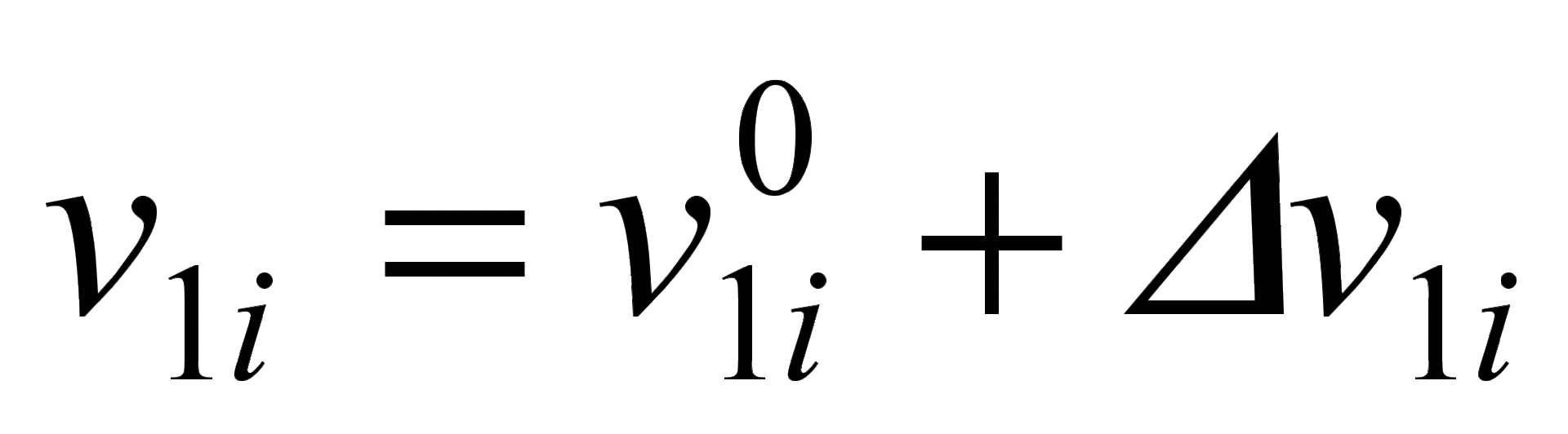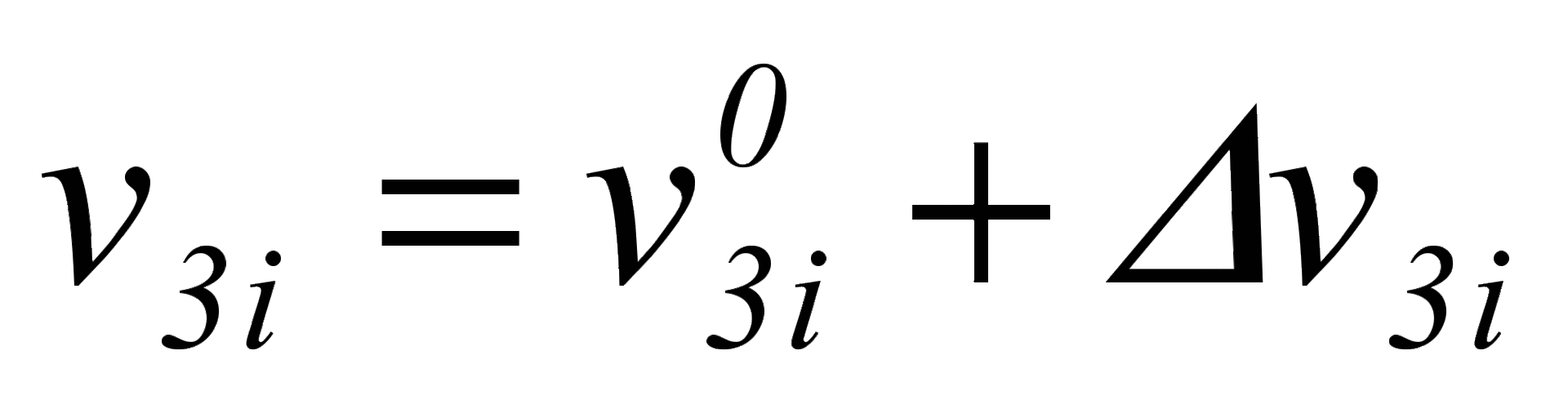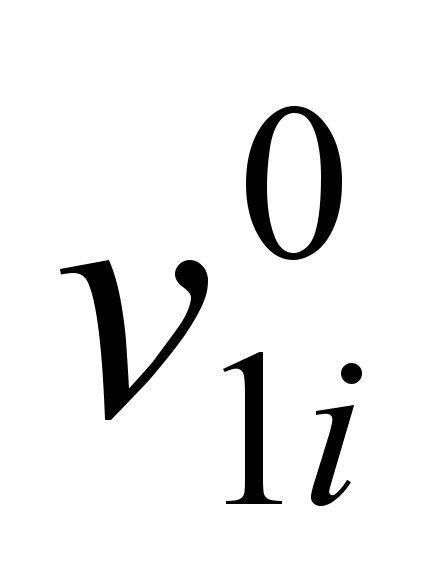, где и 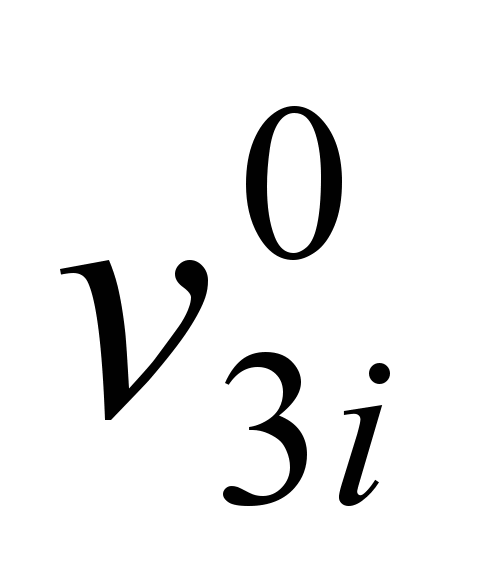— входной и выходной сигнал до изменения,

.

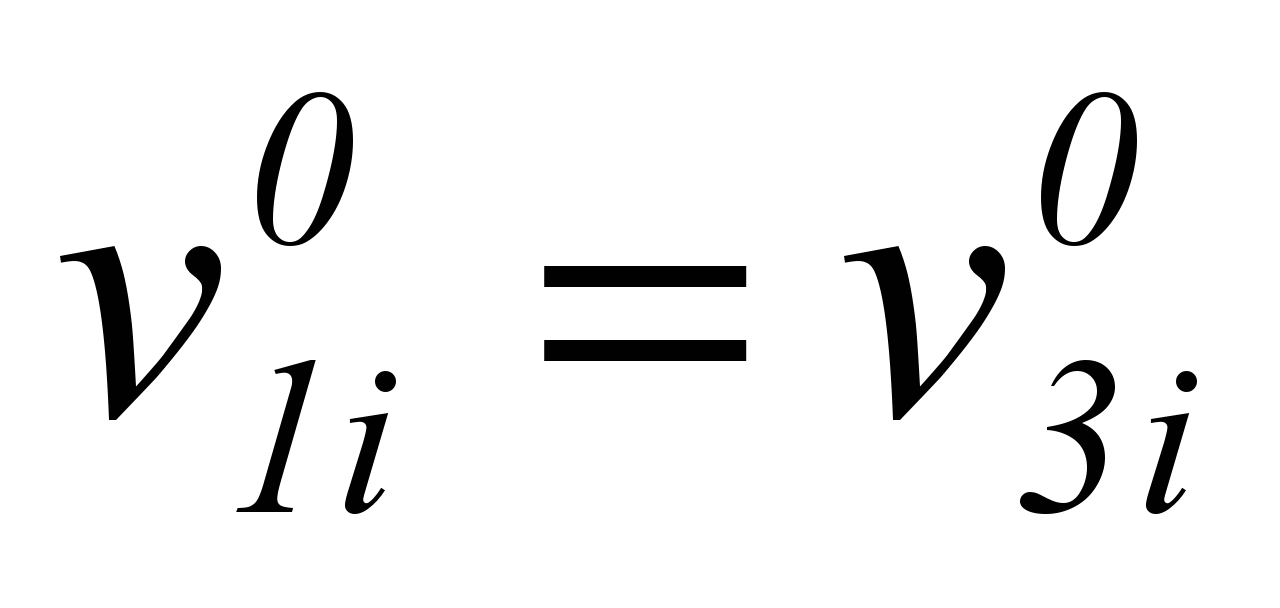Допустим, что производилось изменение только i-го входного сигнала.

Из этих условий следует:

;

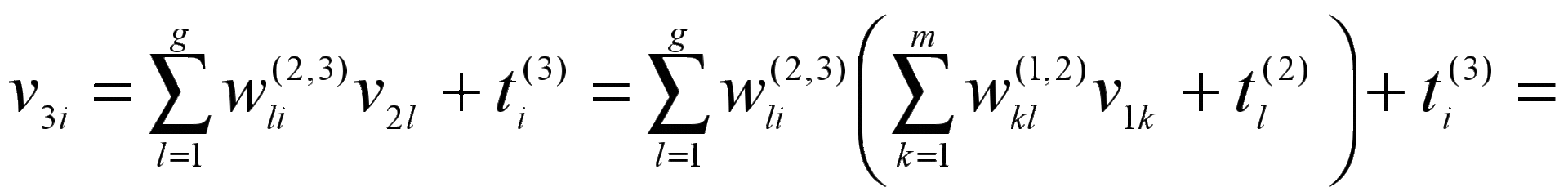
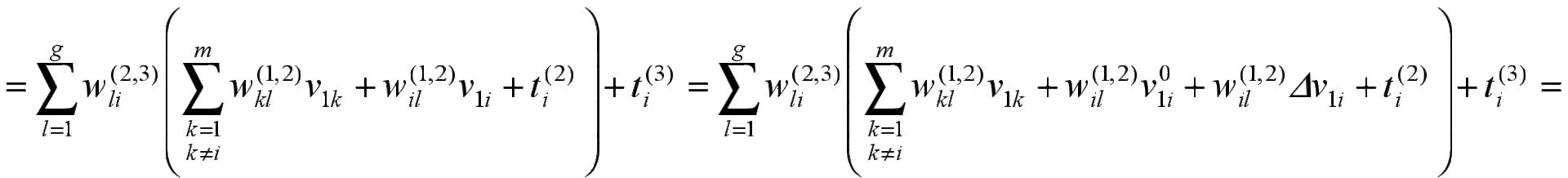
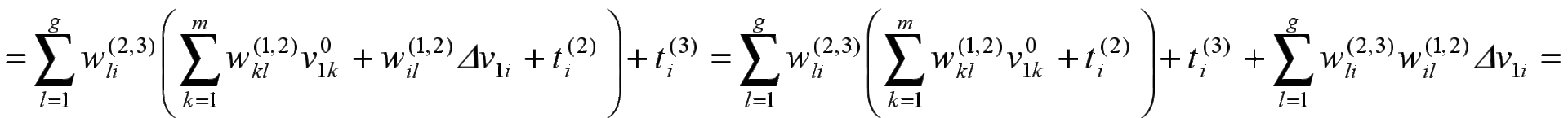
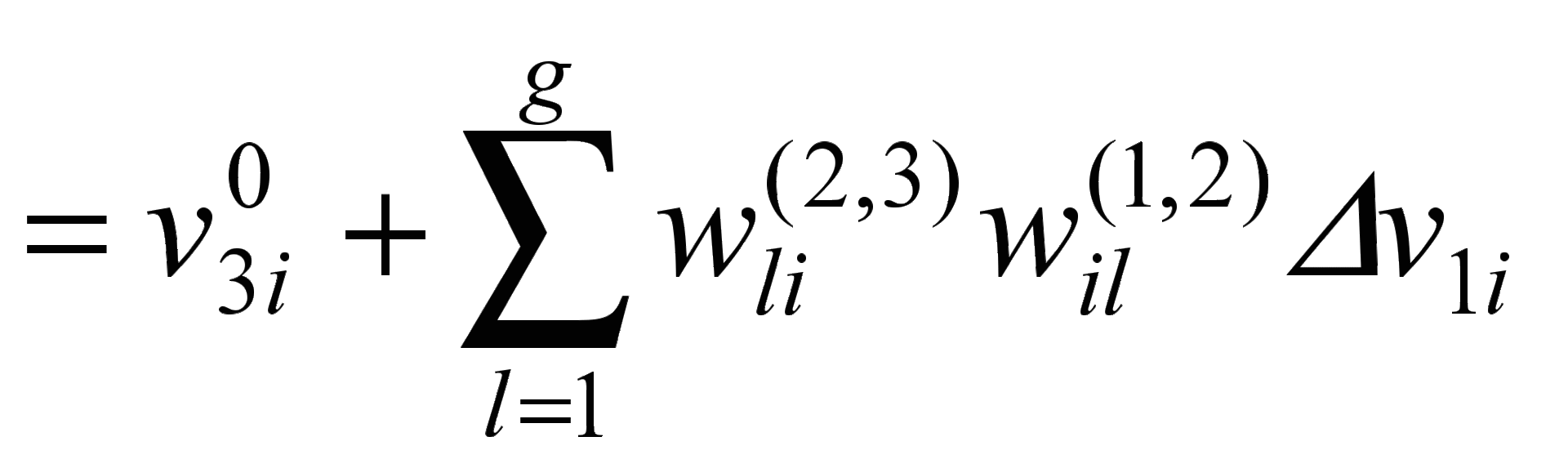
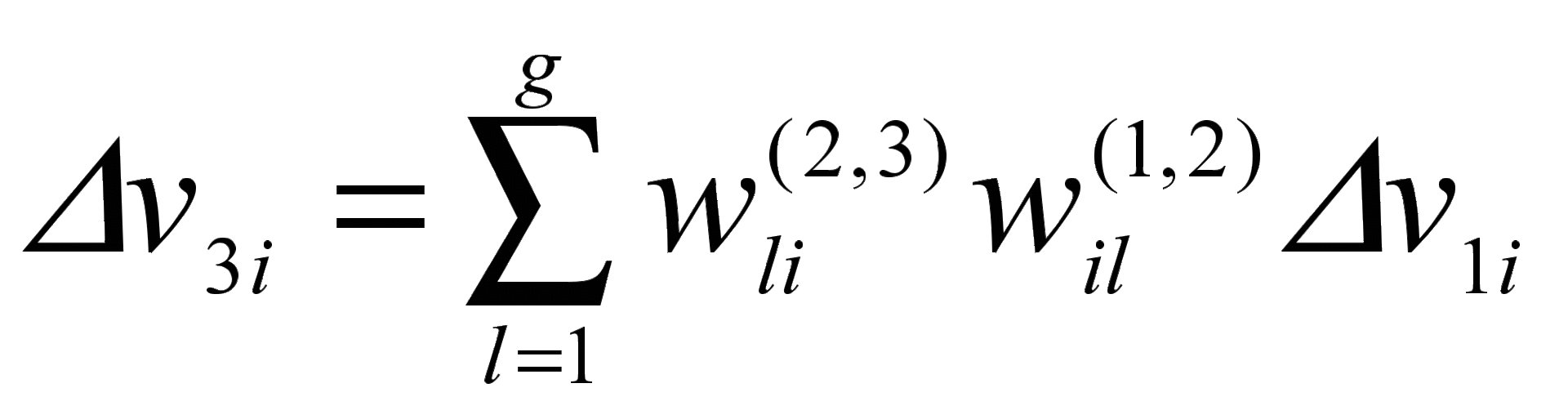Поскольку , то 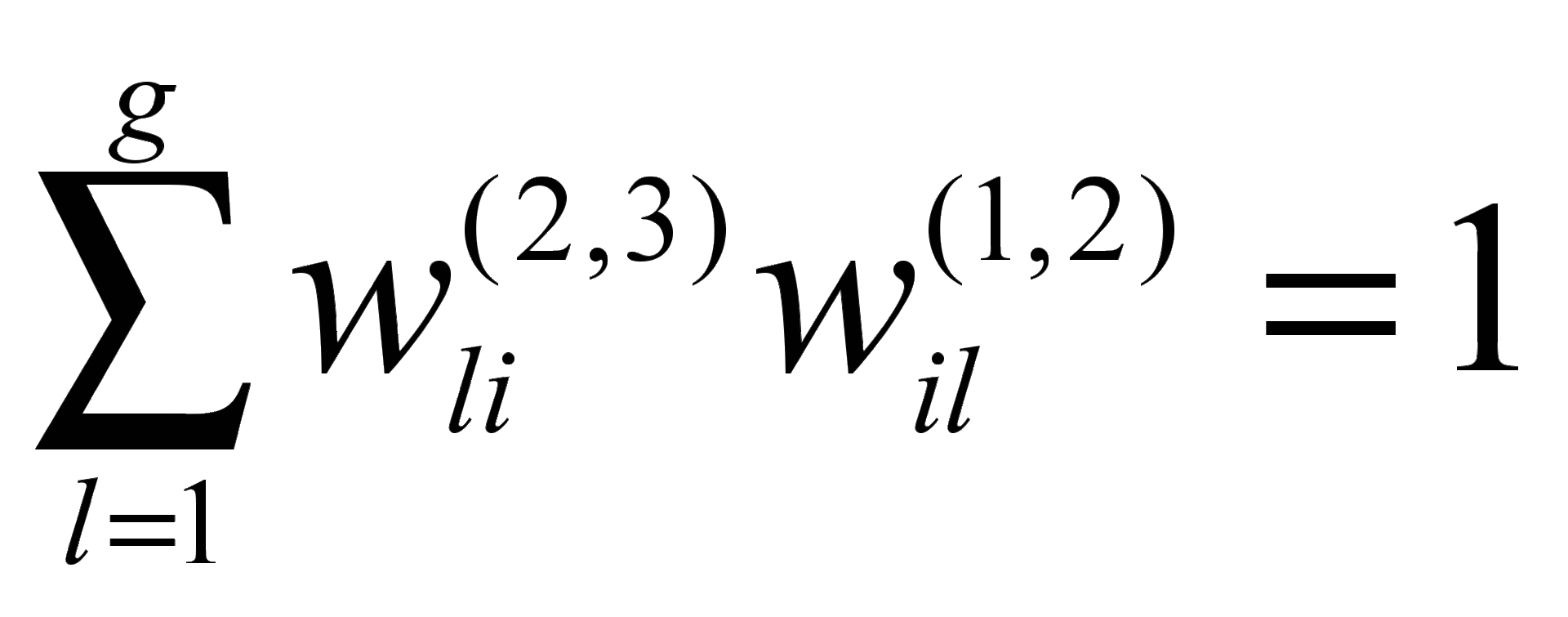должно выполняться для всех i, поскольку выбор i-го входного сигнала был произволен.

Теорема доказана ■.

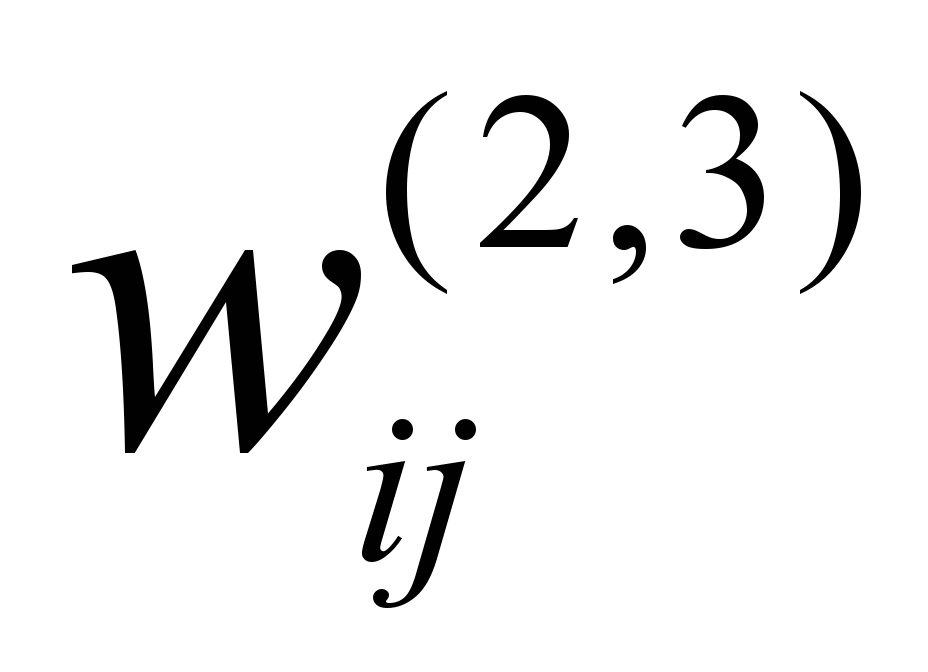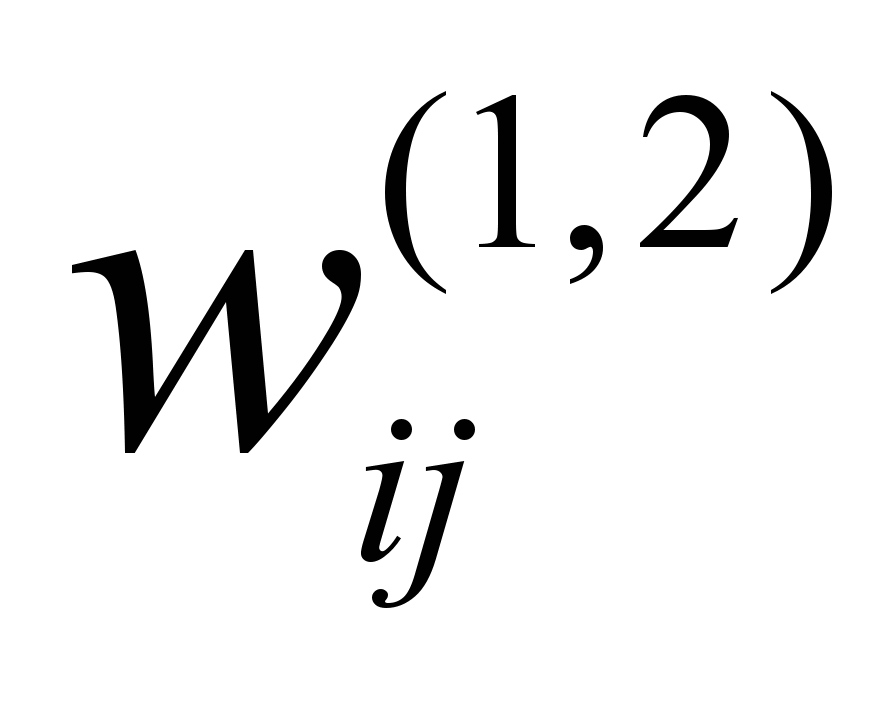Веса и входных сигналов выходного и скрытого слоя нейронной сети с линейной передаточной функцией соответствуют коэффициентам прямого и обратного факторного отображения. Чем точнее нейронная сеть с факторным сжатием информации осуществляет тождественное преобразование, тем точнее будет выполняться равенство теоремы, соответствующее тому, что композиция прямого и обратного факторного преобразования должно давать тождественное преобразование. Докажем соответствующую теорему.

Теорема.

Пусть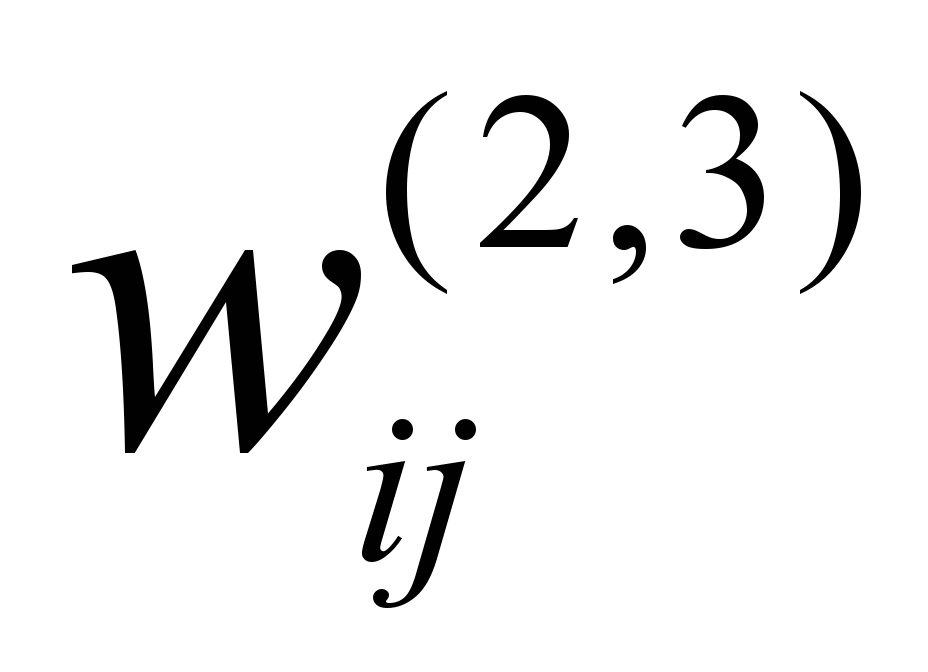и 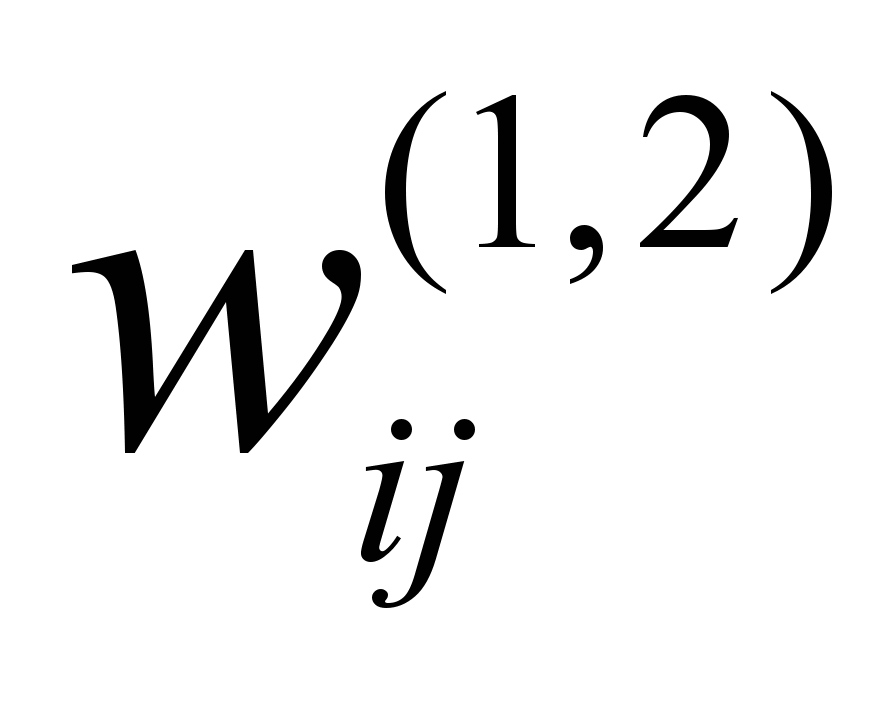− веса входных сигналов выходного и скрытого слоя нейронной сети с линейной передаточной функцией. Число нейронов на выходном слое равно числу нейронов входного слоя. Нейронная сеть состоит из входного, скрытого и выходного слоя.

— средняя невязка сигнала между входом и выходом сети, приходящаяся на один входной (выходной) нейрон,

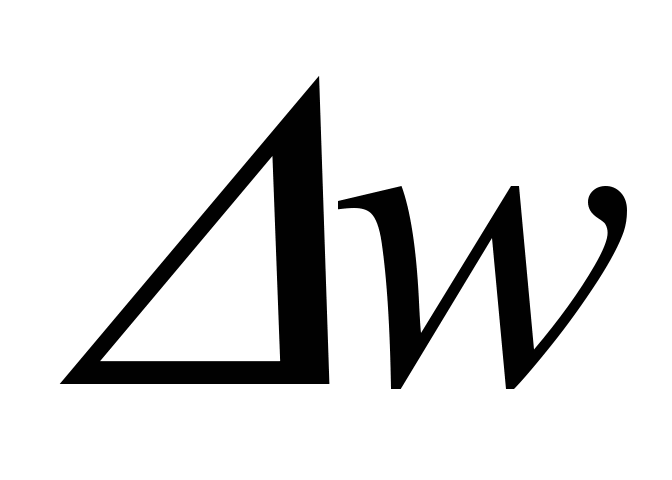–невязка равенства 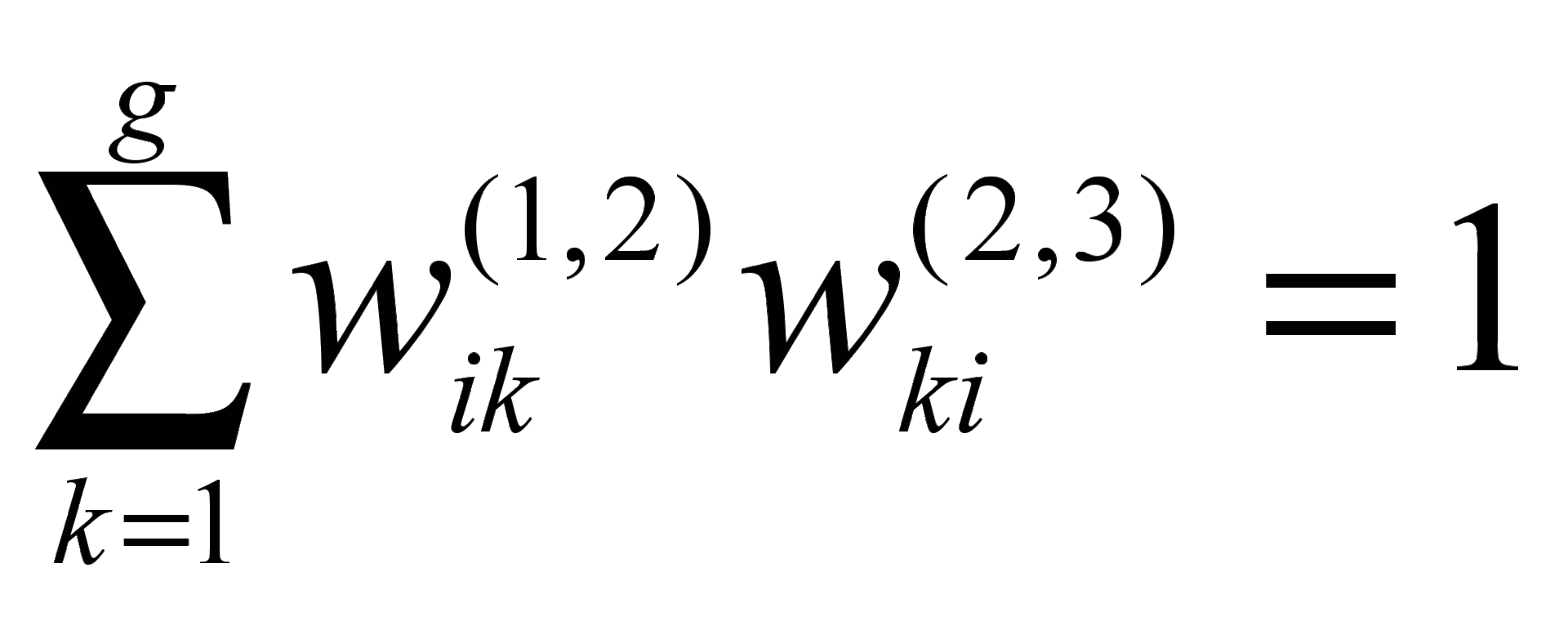, т.е.,

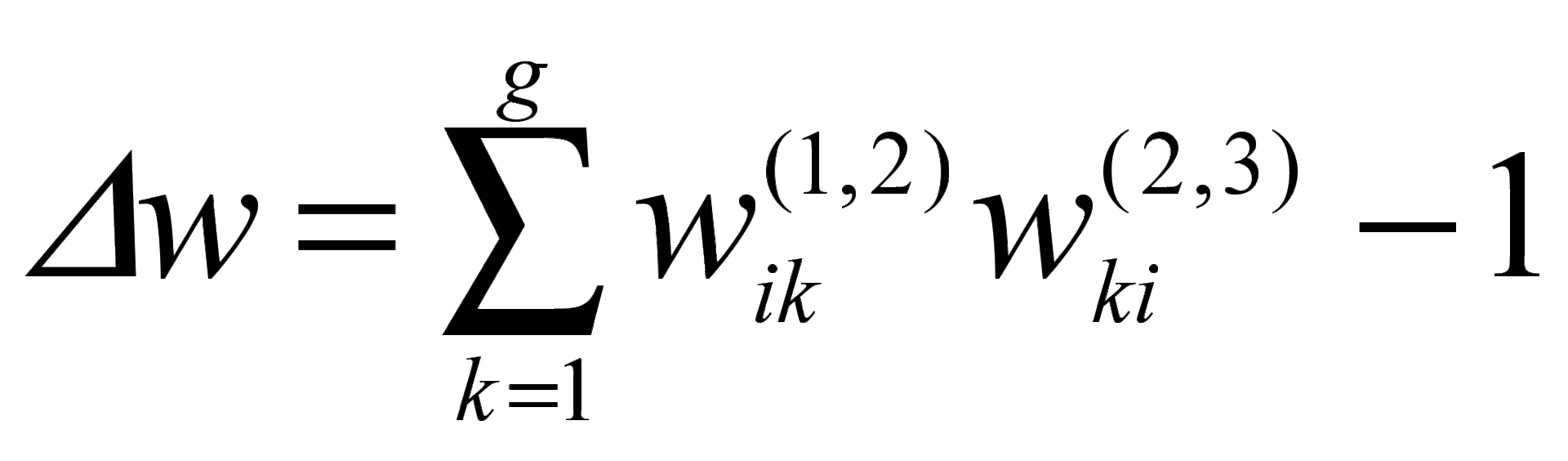где— связь междуi-ым нейрономs-го слоя иj-ым нейрономt-го слоя,

g − число нейронов скрытого слоя.

Тогда чем меньше , тем меньше.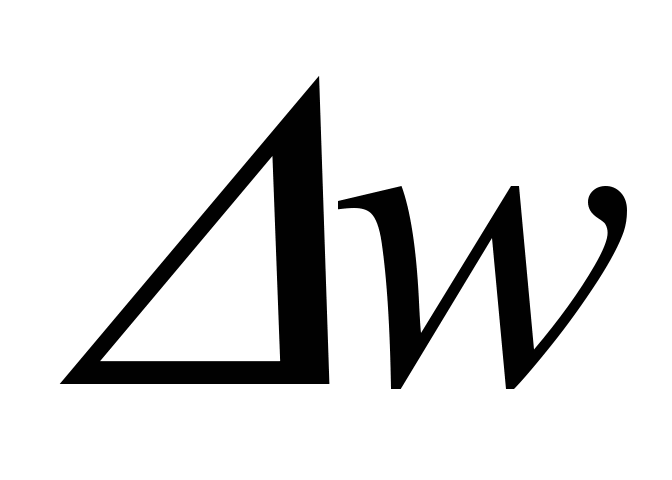

Доказательство:

В предыдущей теореме доказано следующее равенствозначения сигнала по одной переменной на выходе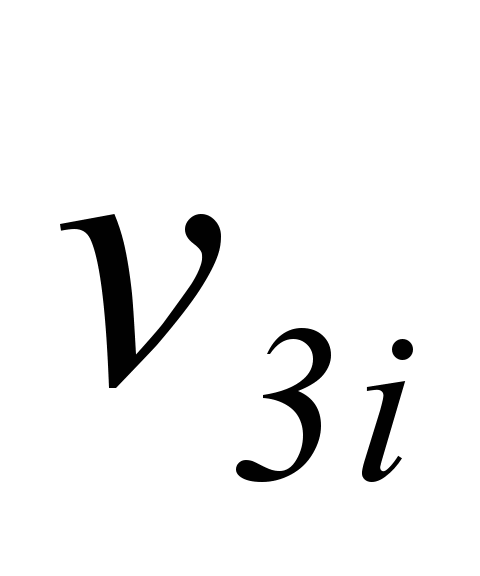от приращения сигнала по той же переменной на входе :

.

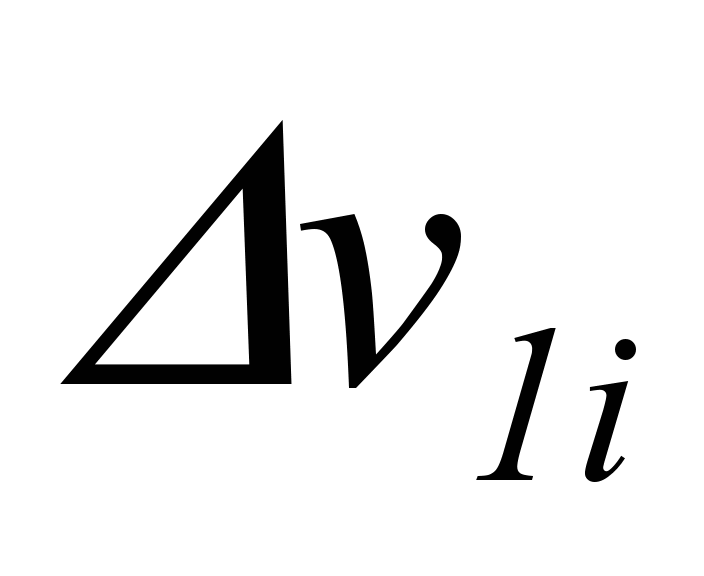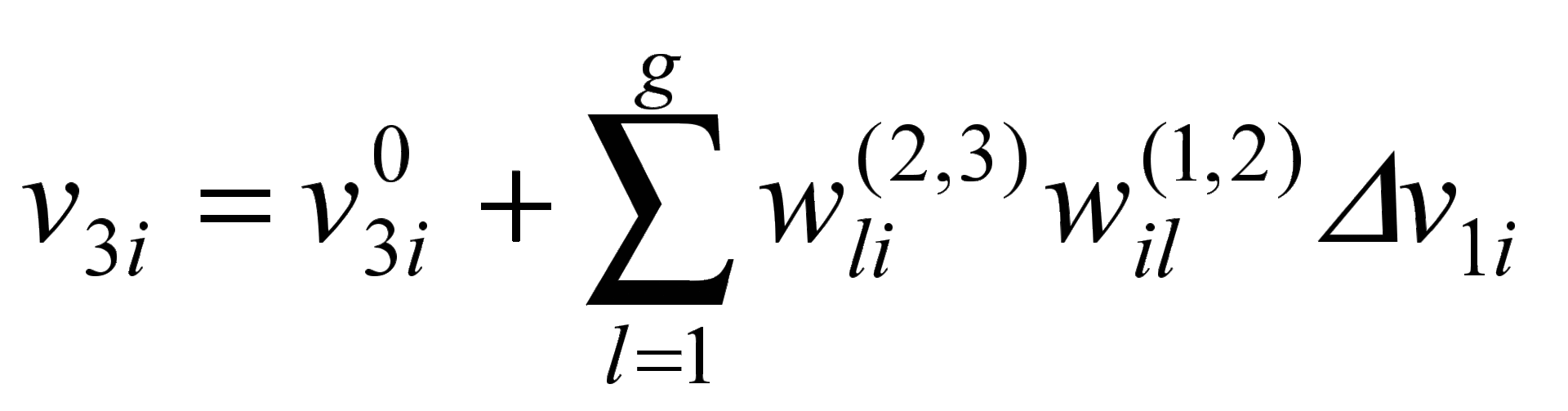Поскольку ,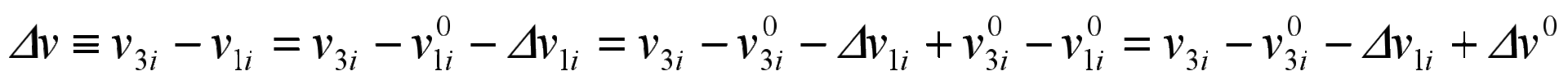

где 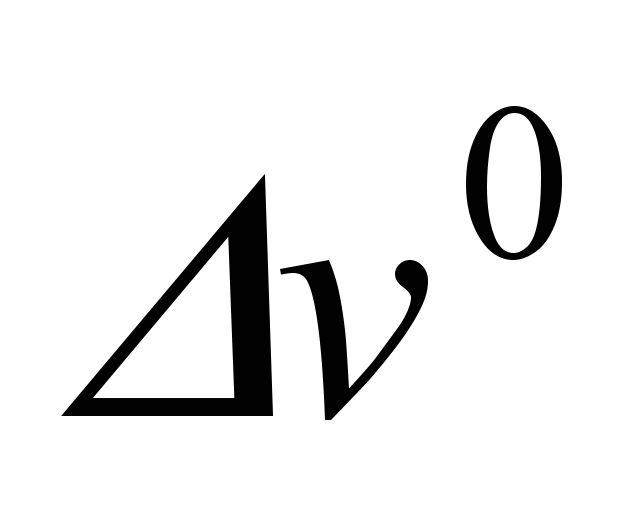— начальная невязка сигналов между входом и выходом сети до изменения i-го входного сигнала,

то 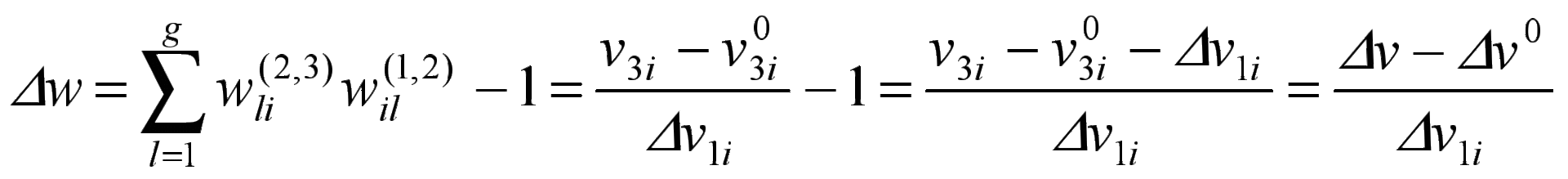. Это означает монотонную зависимость между 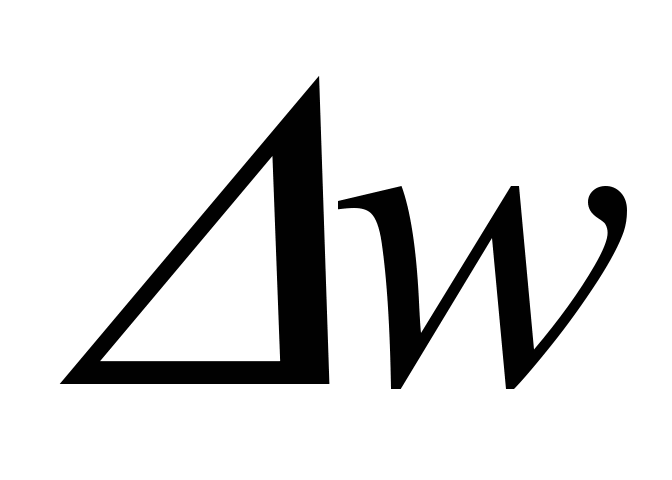и .

Теорема доказана ■.

Для построения нелинейных главных компонент в качестве передаточной функции может быть выбрана антисимметричная сигмоидальная функция:

.

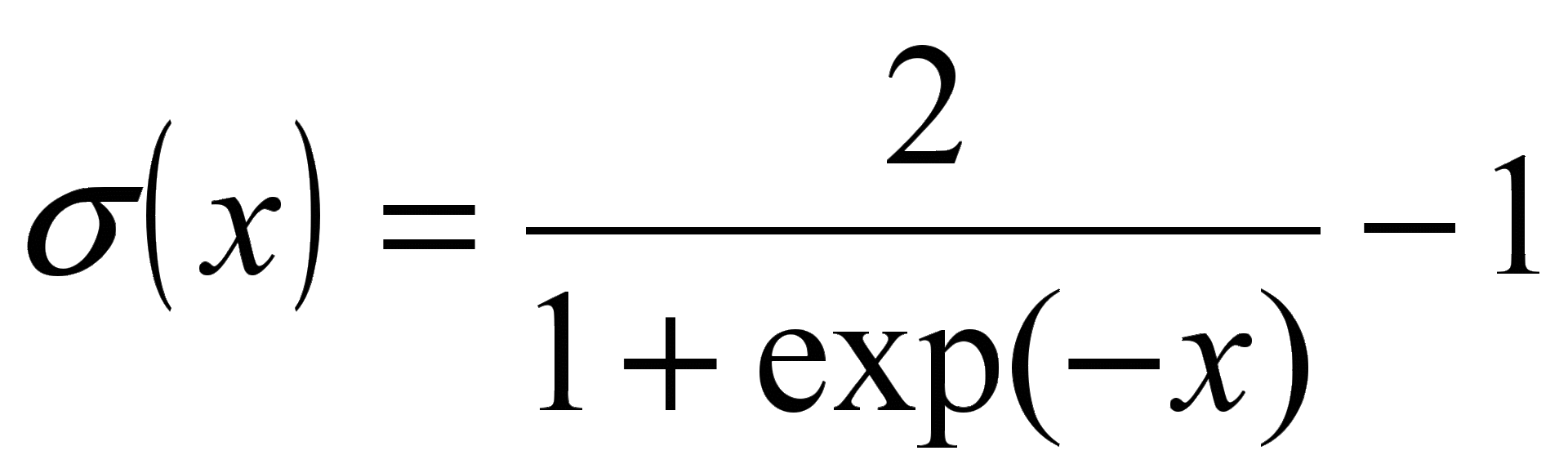В любом случае независимо от вида передаточной функции для получения интерпретируемого факторного отображения вводится дополнительное слагаемое в общую целевую функцию квадратов невязок, соответствующее критерию «варимакс» классического факторного анализа — это максимизация дисперсии нагрузок переменной, приходящихся на все факторы:

,

.

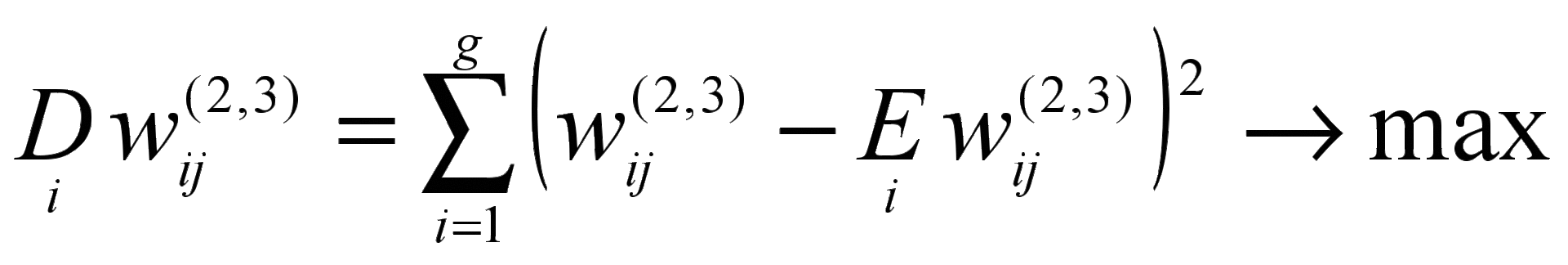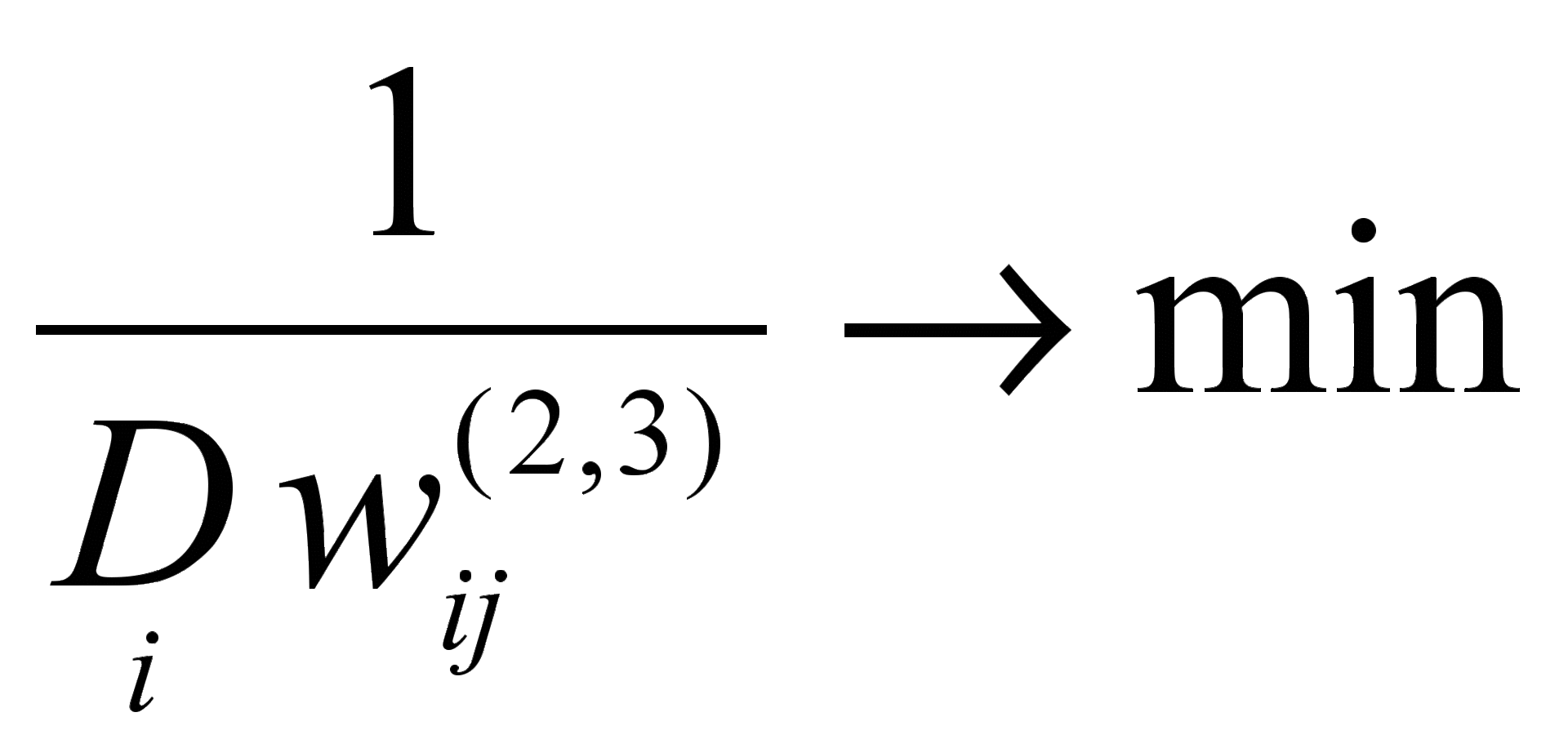Учет «варимакс» критерия приводит к появлению дополнительных слагаемых при изменении весов нейронной сети на выходном слое:

.

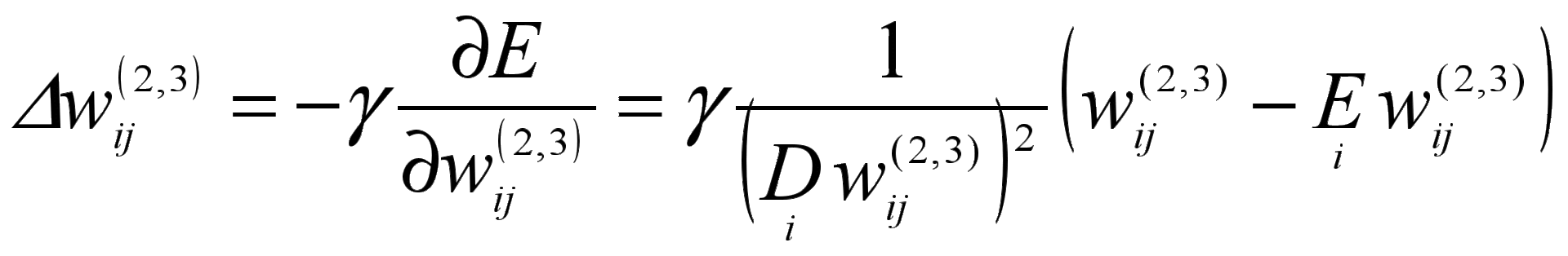Другим вариантом получения интерпретируемого факторного отображения может быть использование специального критерия интерпретируемости [12]. Данный критерий заключается в том, что только одна факторная нагрузка для фиксированной переменной, должна быть близкой к 1, тогда как остальные должны быть близкими к 0. Учет эмпирического критерия интерпретируемости, предлагается осуществить следующим образом: среди факторных нагрузок для фиксированной переменной выбирается максимальная по модулю. Все факторные нагрузки отличные от максимальной уменьшаются по модулю на γ, тогда как максимальная увеличивается на γ.

Аналогичный учет главных условий факторного анализа на сумму квадратов факторных нагрузок переменной, приходящихся на все факторы, 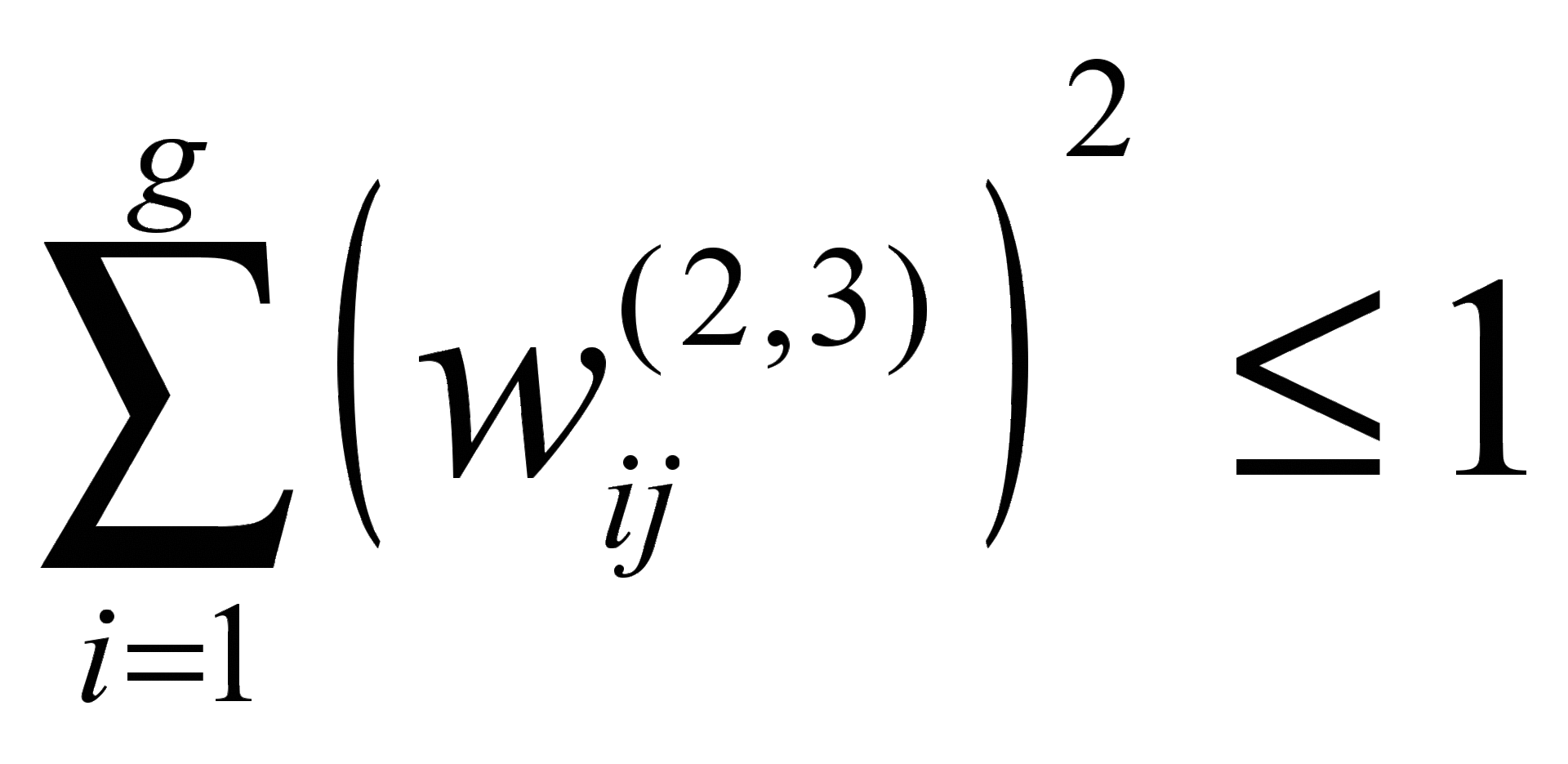и поиск факторных нагрузок в допустимом интервале 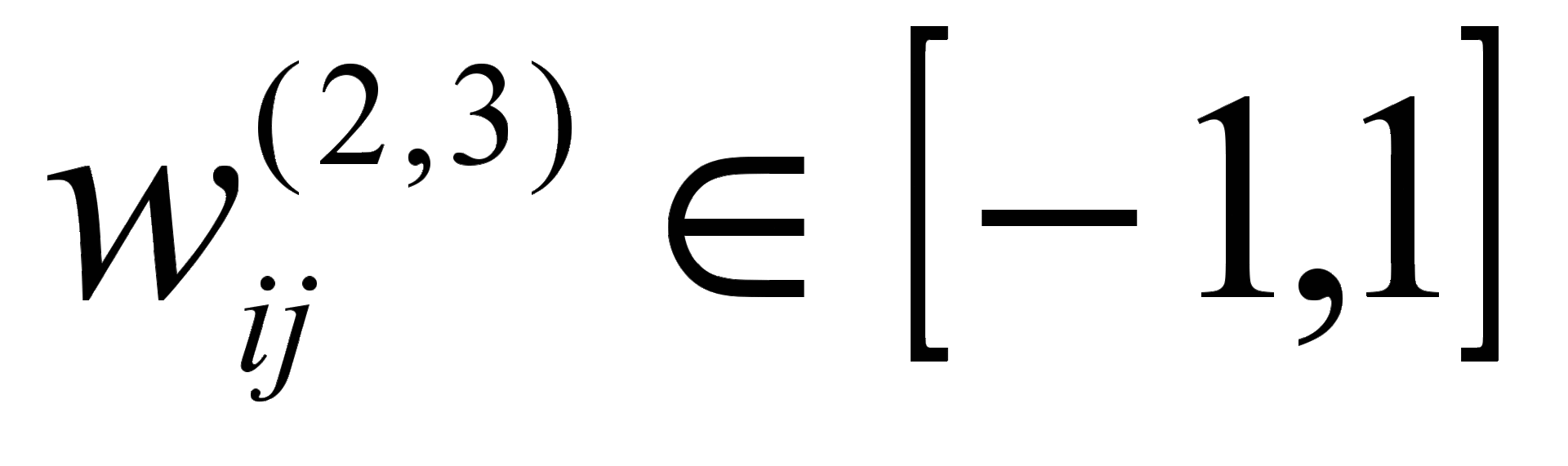приводит к поправкам на изменение весов нейронной сети для выходного слоя. В случае нарушения этих условий предлагается использовать штрафную функцию 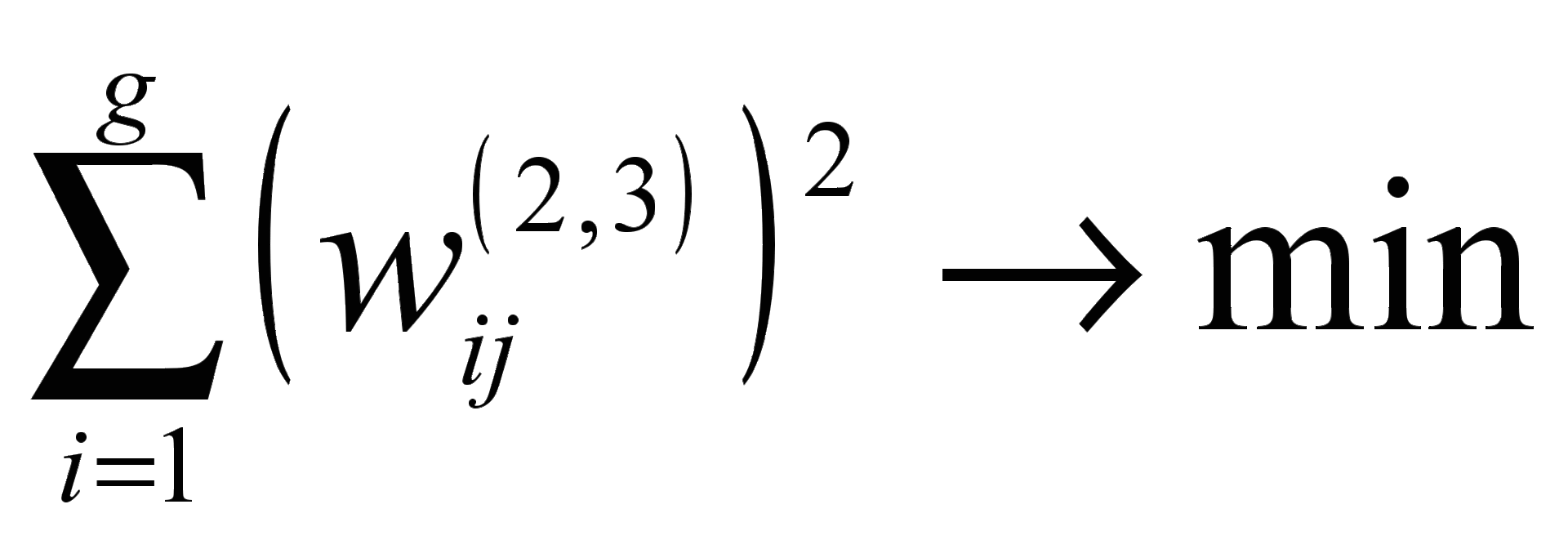, соответствующую минимизации весов нейронов. Тогда .

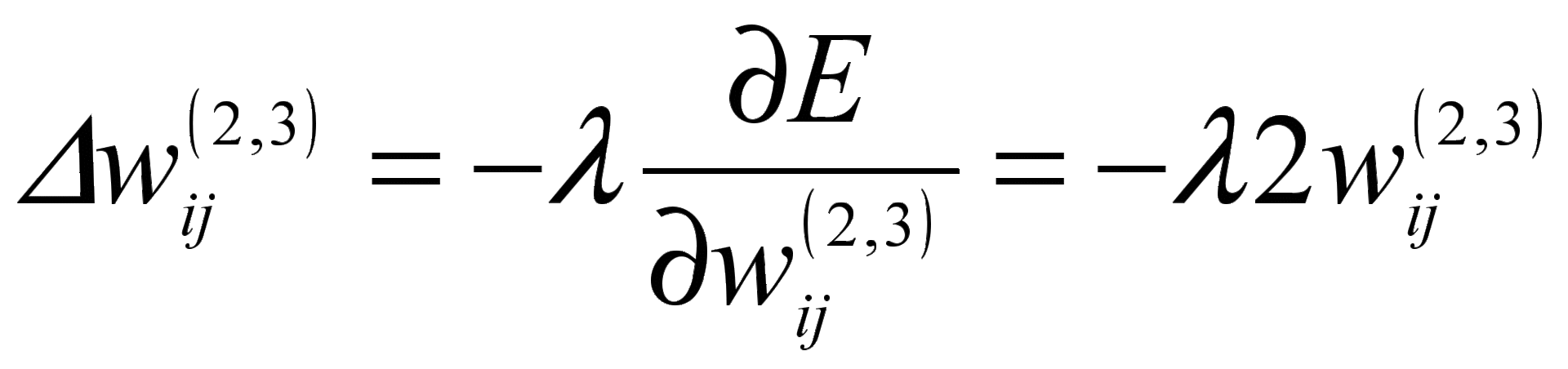Для стандартизации входных значений нейронной сети используется линейное преобразование:

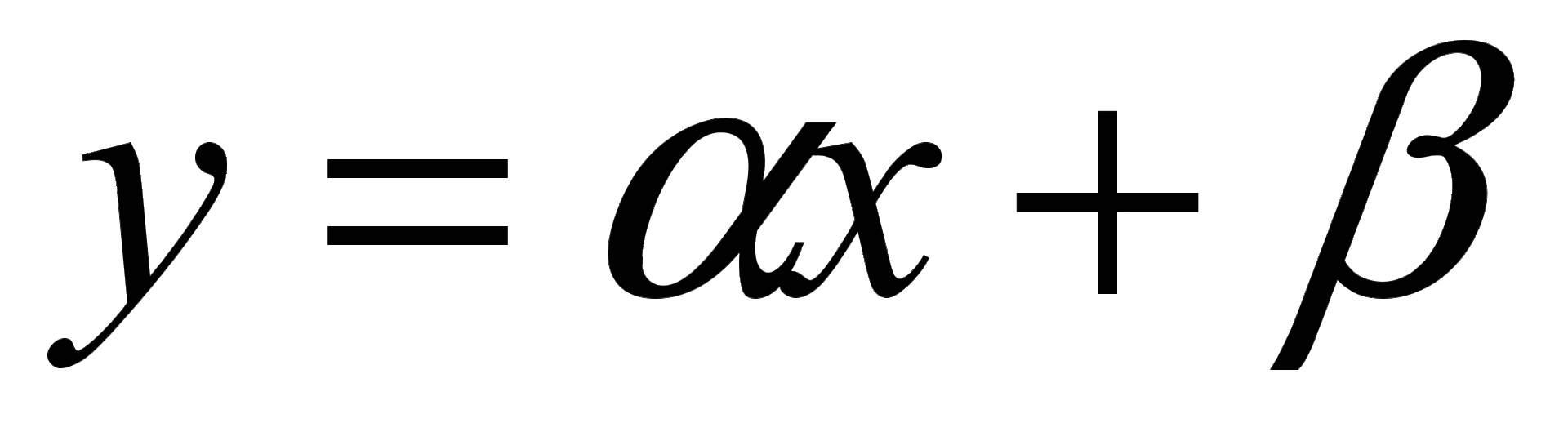, переводящее диапазон исходных величинxиз [min, max] в [s, t].

Тогда , .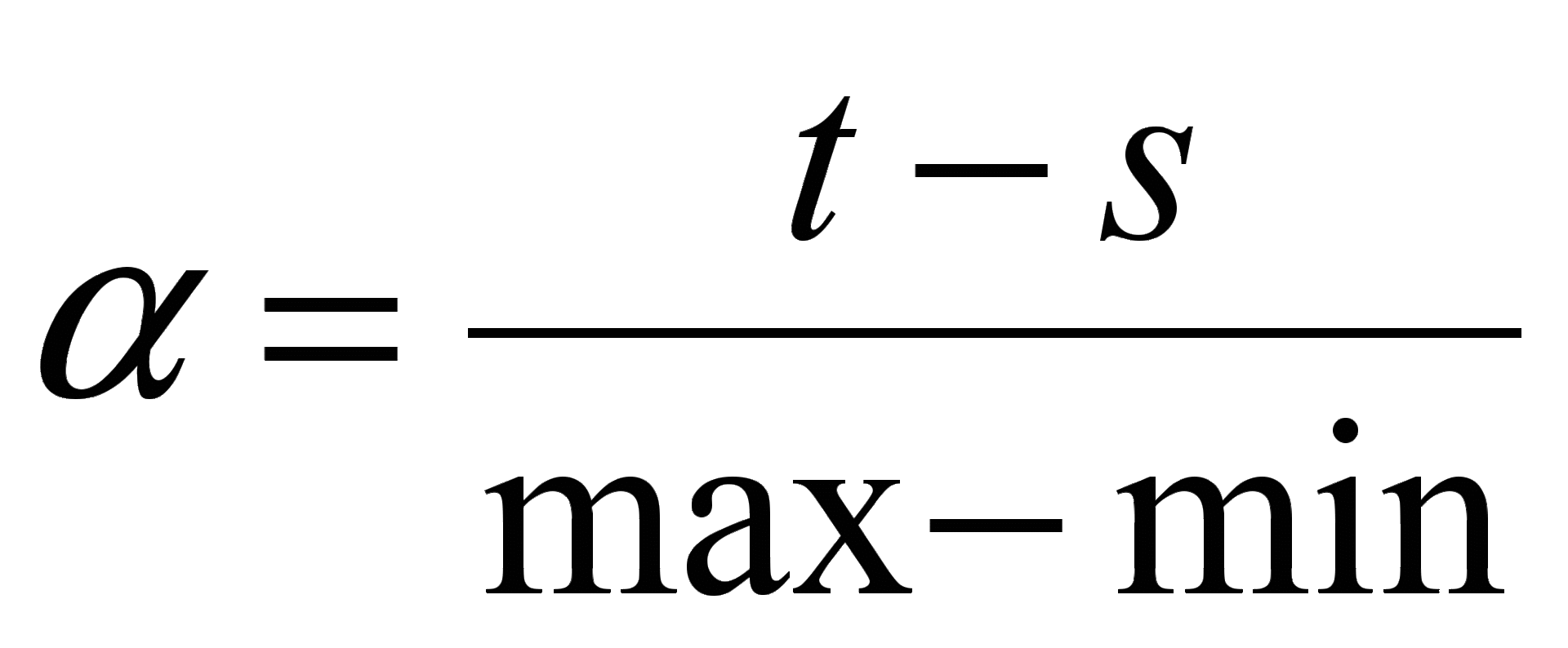

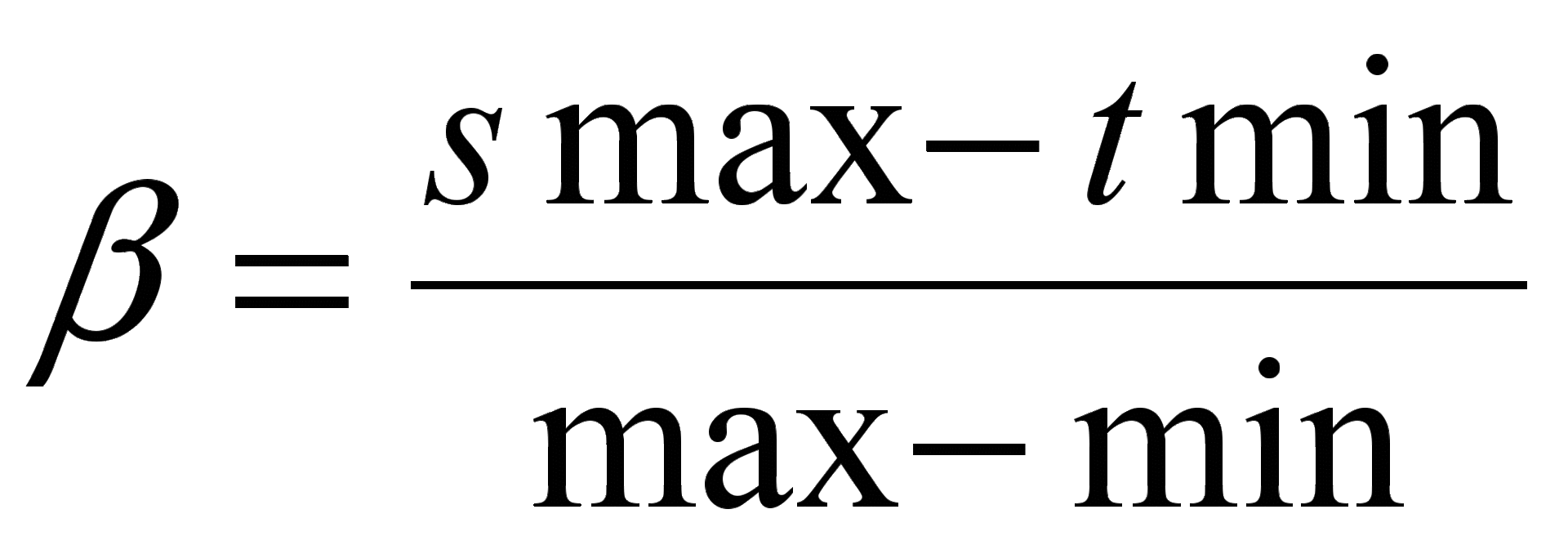Для обратного преобразования выходных значений нейронной сети из диапазона [s, t] в [min, max] используется преобразование .

В качестве интервала [s, t] для антисимметричной сигмоидальной функции 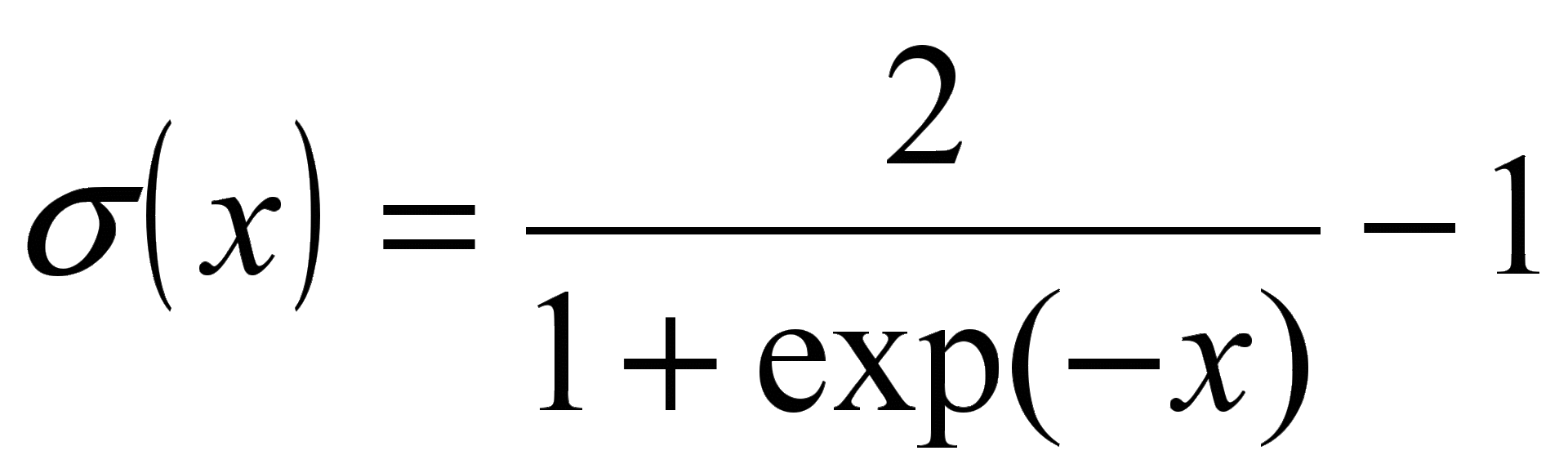может быть выбран интервал [-0.85, 0.85].

Тогда , .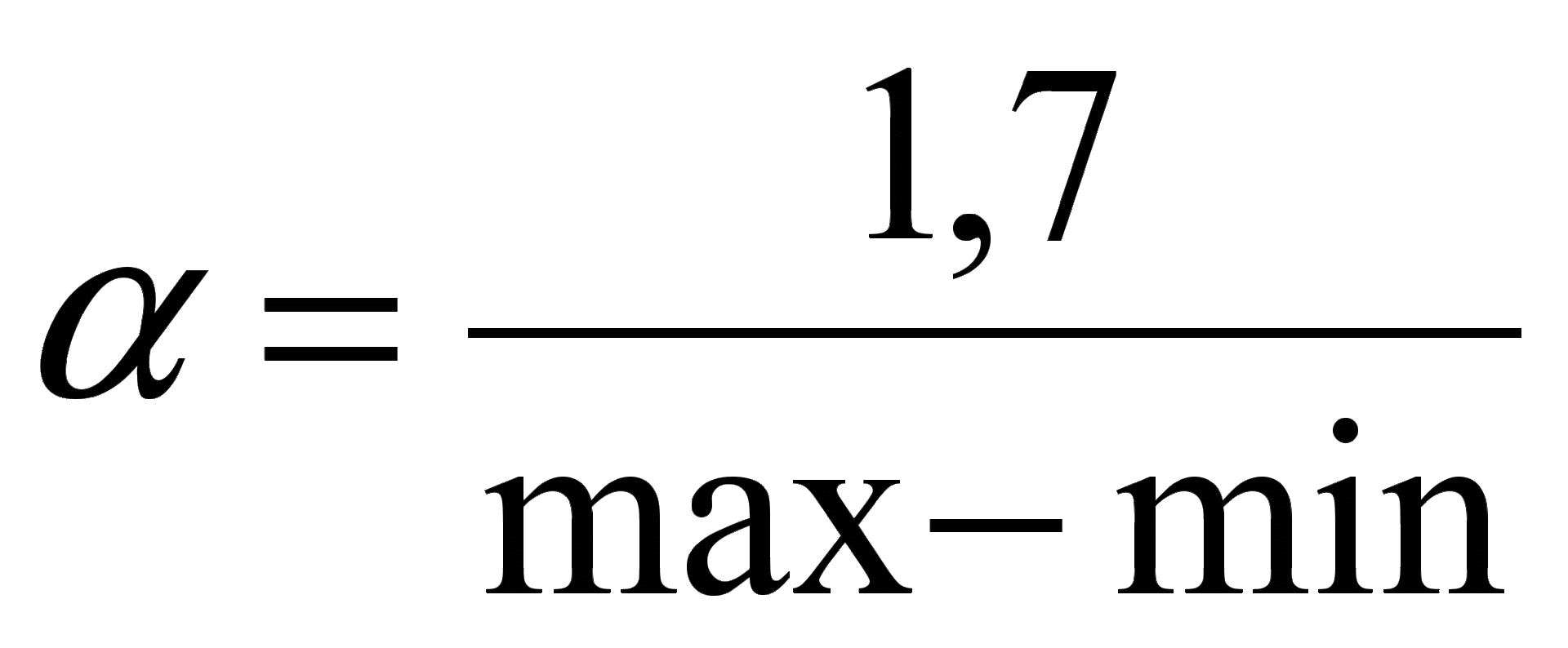

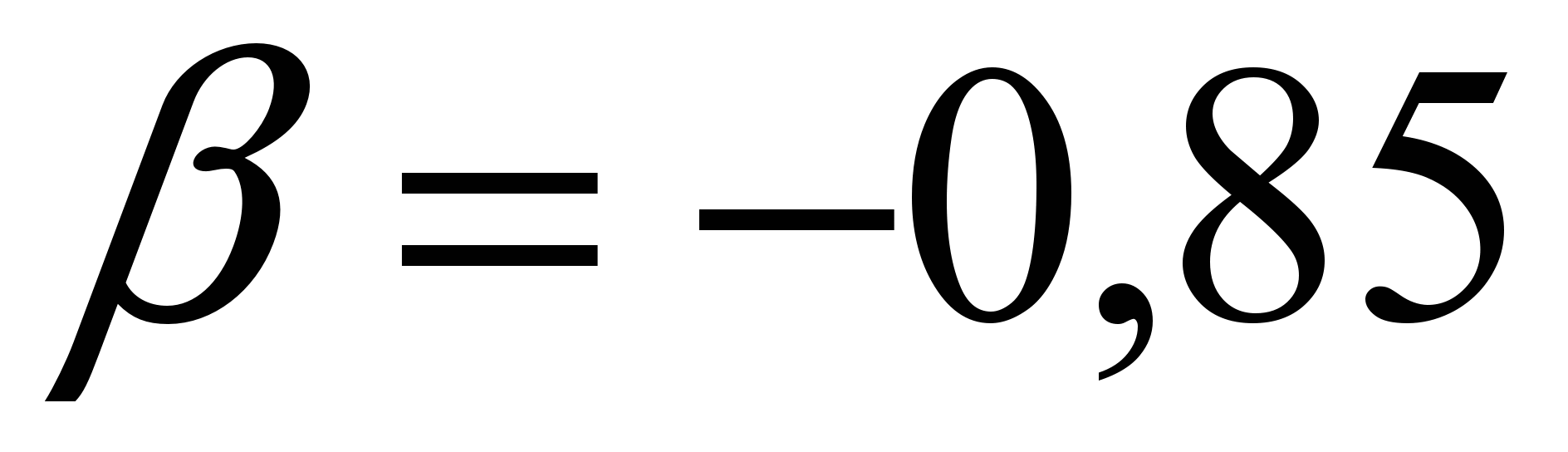Численный эксперимент. В качестве исходных параметров были взяты 15 биофизических показателей для 131 лица с артериальной гипертензией начальной стадии:

1. вес,

   
   

2. индекс массы тела (ИМТ),

   
   

3. частота дыхания (ЧД),

   
   

4. сегментоядерные нейтрофилы ©,

   
   

5. лимфоциты (Л),

   
   

6. конечно-систолический размер левого желудочка (КСР),

   
   

7. конечно-систолический объем левого желудочка (КСО),

   
   

8. конечно-диастолический размер левого желудочка (КДР),

   
   

9. конечно-диастолический объем левого желудочка (КДО),

   
   

10. ударный объем (УО),

    
    

11. минутный объем сердца (МОС),

    
    

12. общее периферическое сосудистое сопротивление (ОПСС),

    
    

13. индекс Хильдебрандта (ИХ),

    
    

14. фракция выброса левого желудочка (ФВ),

    
    

15. фракция укорочения левого желудочка (ФУ).

    
    

При обучении нейронной сети на данных артериальной гипертензии начальной стадии содержащих 131 паттерн и 15 переменных с антисимметричной сигмоидальной передаточной функцией и 5-ю нейронами на скрытом слое ошибка, приходящаяся на одну переменную, составляла не более 10% от диапазона значений переменной по выборке. График сходимости процесса обучения представлен на рисунке 3. Под итерацией обучения понимается одна эпоха обучения, когда сети подставляется весь набор паттернов обучения. Под суммарной ошибкой на обучающей выборке понимается сумма ошибок для всех паттернов обучающего множества на одной итерации обучения.

Для проверки эффективности обучения нейронной сети исходное множество входных-выходных значений было разделено на 2 независимых подмножества: обучающее и тестовое. Обучение проводилось на обучающем множестве, а верификация — на тестовом. Ошибка нейронной сети на тестовом множестве является показателем того, насколько точно обучилась нейронная сеть. Относительный объем тестового множества был оценен по формуле [7]:

,

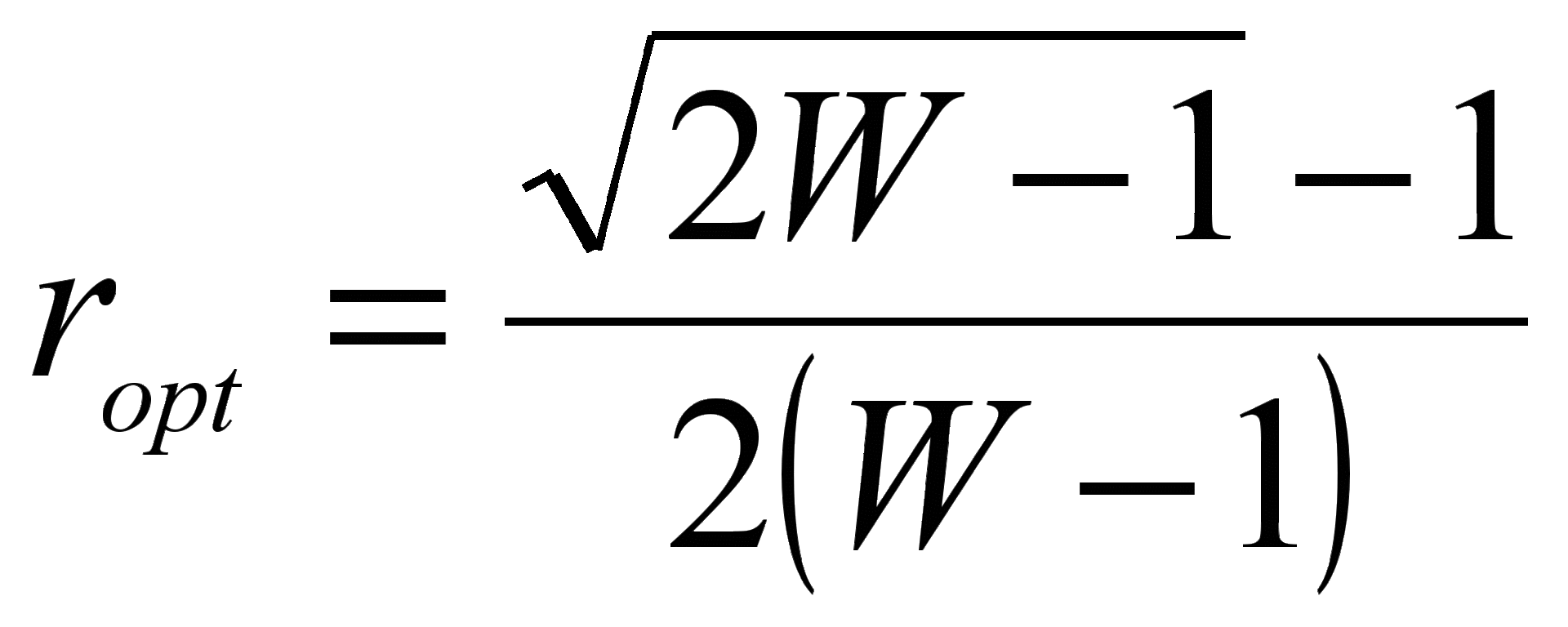где W− количество входных параметров.

При W= 15, 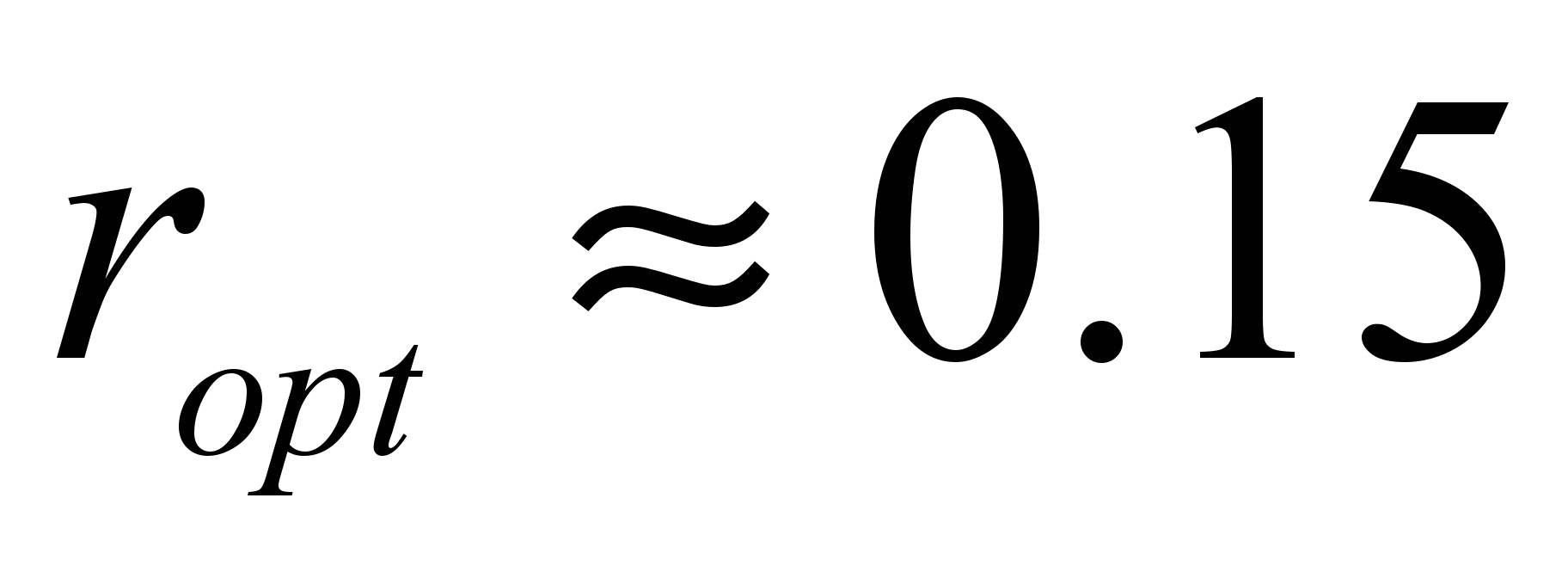. При 131 паттерне на тестовое множество приходится 20 паттернов.

График изменения суммарной ошибки для паттернов тестового множества при верификации на каждой эпохе процесса обучение представлен на рисунке 4. Под суммарной ошибкой на тестовом множестве понимается сумма ошибок для 20 паттернов тестового множества при процессе верификации на каждой эпохе обучения, т.е. когда для обучения был использован полный набор паттернов обучающего множества, но тестовое множество не участвовало в обучении. На каждой эпохе относительная ошибка для тестового множества больше относительной ошибки для обучающего множества. В пределе, когда ошибка для обучающего множества начинает сходится, возможен эффект переобучения, т.е. значение ошибки при верификации на тестовом множестве начинает не уменьшатся, а расти это связано с тем, что промежуточные точки между точками обучающего множества в многомерном пространстве плохо аппроксимируются восстанавливаемой зависимостью нейронной сети. Рисунок 4 и его график изменения ошибки на тестовом множестве показывает, что эффекта переобучения нет и объем обучающего множества достаточен для количества исходных показателей равным 15. На графики заметны лишь незначительные флуктуации ошибки при дальнейшем обучении на обучающем множестве в процессе сходимости ошибки для обучающего множества.

Из графика видно, что эффекта переобучения не наблюдается, дальнейшее обучение приводит лишь к небольшой флуктуации суммарной ошибки на тестовом множестве.

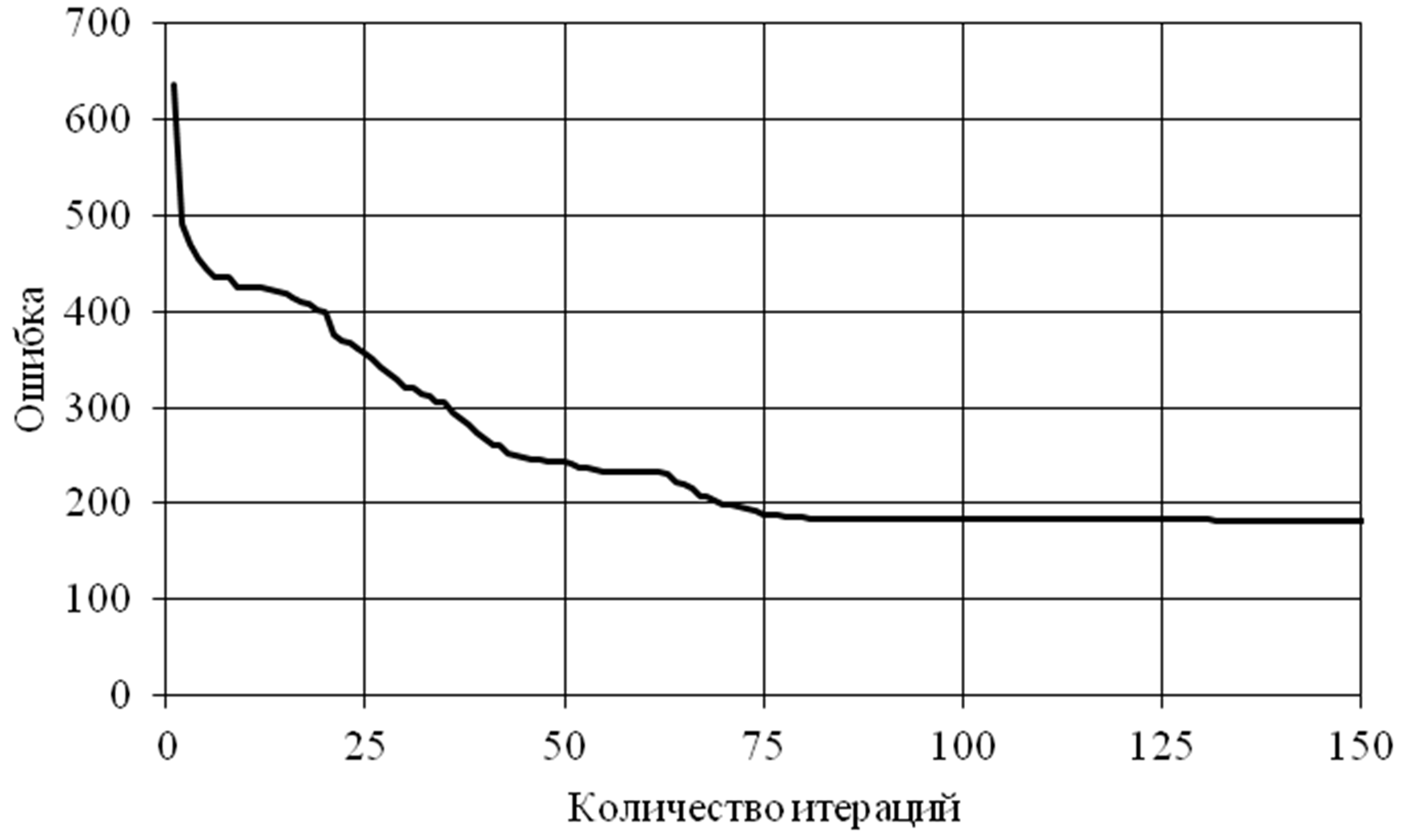
Рис. 3.График изменения суммарной ошибки на обучающей выборке (131 паттерн, 15 переменных).

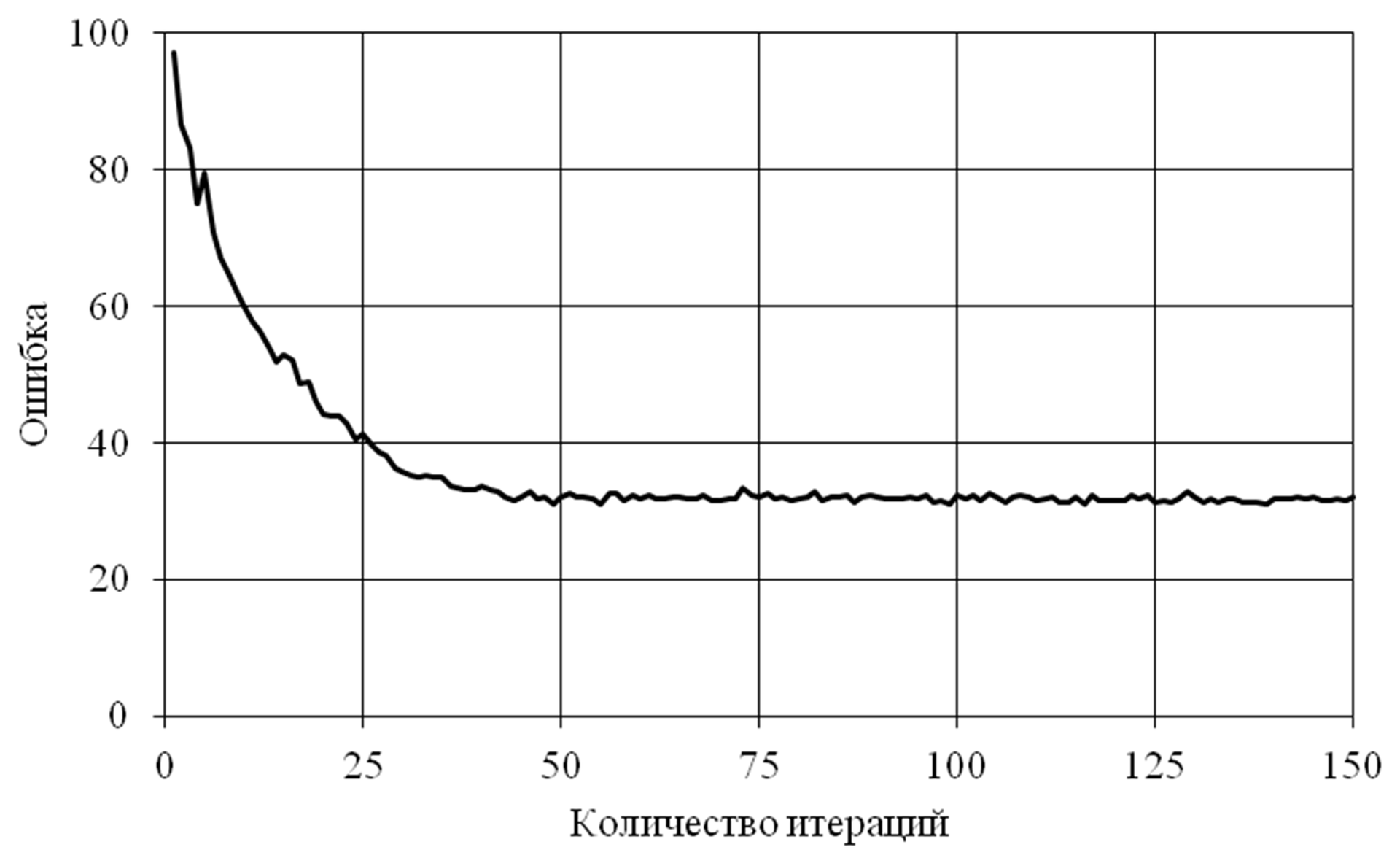
Рис. 4.График изменения суммарной ошибки на тестовом множестве (20 паттернов, 15 переменных).

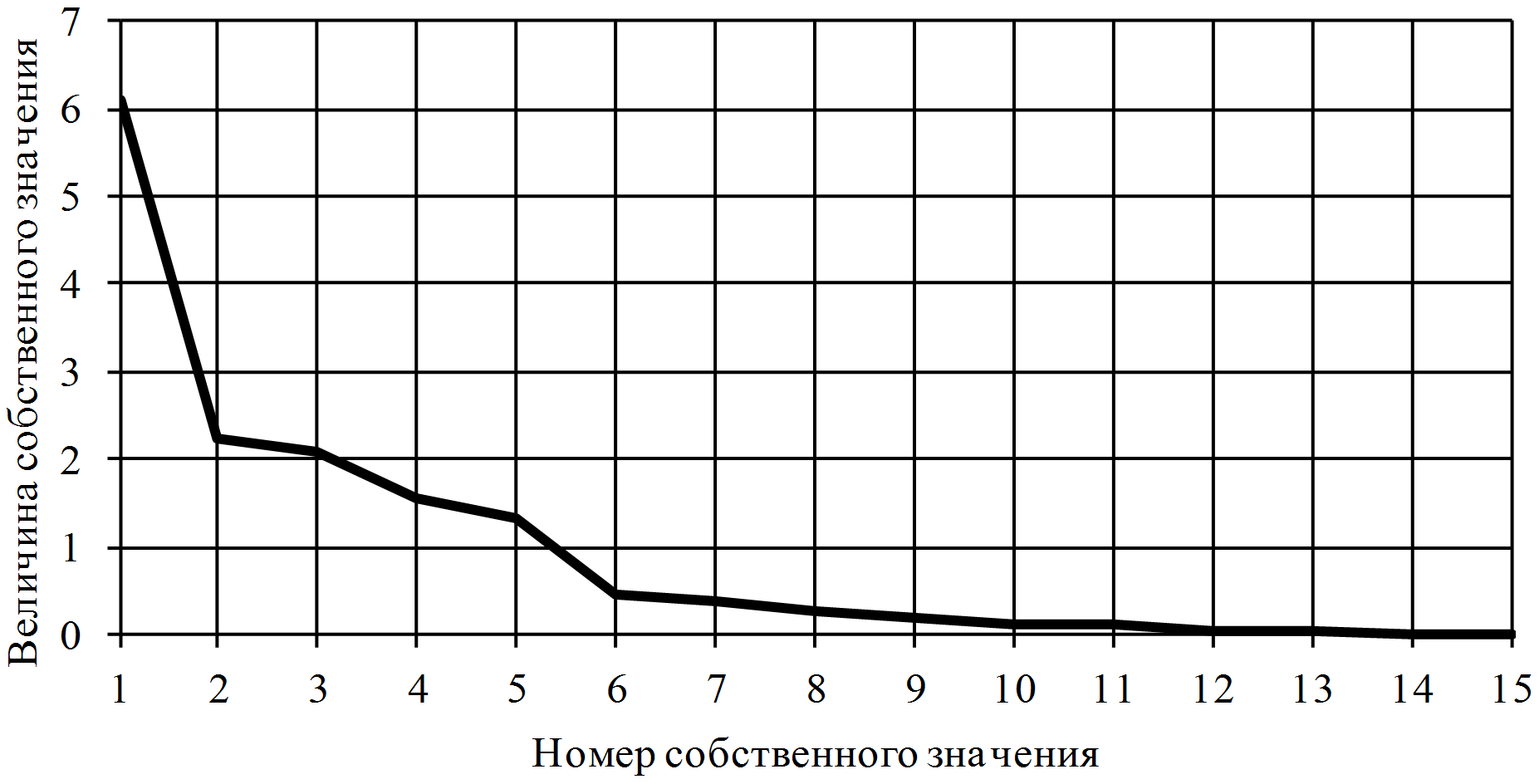
Рис. 5.Собственные значения исходных переменных.

Средние ошибки, приходящиеся на 15 переменных для одного паттерна на обучающем и тестовом множестве равны 1.28 и 1.54. При исходном диапазоне изменения параметров [-0.85, 0.85] ошибка, приходящаяся на одну переменную, для обучающего и тестового множества равны 5 и 6%. Например, для параметра »вес» наибольший вес был равен 116 кг, наименьший 45 кг, при диапазоне в 71 кг, ошибка в 6% соответствует 4.26 кг. Это свидетельствует о хорошей способности нейронной сети к обобщению. Поскольку ошибка в 6% для 15 входных параметров и 131 примера для обучения меньше теоретической оценки ошибки в 10%, когда требуется 15×10 примеров для обучения, то можно говорить о достаточности обучающего множества. Известно, что между действительно достаточным размером множества обучения и теоретическими оценками может существовать большой разрыв [7].

Число нейронов на скрытом слое выбиралось согласно правилу Кайзера факторного анализа, когда число факторов выбирается не больше чем количество собственных значений корреляционной матрицы переменных больших 1. График собственных значений исходных переменных приведен на рисунке 5. В ходе численного эксперимента с данными артериальной гипертензии было установлено, что хорошая обучаемость нейронной сети достигается при числе нейронов в скрытом слое не меньшем верхней границы числа собственных значений исходных переменных по правилу Кайзера. При меньшем числе нейронов в скрытом слое наблюдались значительные ошибки на обучающей выборке и наоборот, чем больше нейронов выбиралось на скрытом слое, тем меньше была ошибка на тестовом и обучающем множестве. Это связано с факторным сжатием и потерей информации на скрытом слое.

Факторное отображение, полученное с помощью нейронной сети, незначительно отличается от факторного отображения, получаемого методом главных компонент с последующим «варимакс» вращением и имеет тот же интерпретационный характер, все значимые факторные нагрузки двух матриц факторных отображений близки друг к другу. Соответствующие факторные структуры приведены в таблице 1, 2, 3.

С точки зрения совпадения факторных структур ошибка прогноза входного паттерна менее 10% оказалась не критичной и нейронная сеть является достаточно обученной для проведения факторного анализа. Данные факторные структуры подтверждаются предыдущими работами [11].

Таблица 1. Факторная структура «варимакс»

(метод главных компонент + «варимакс» вращение)

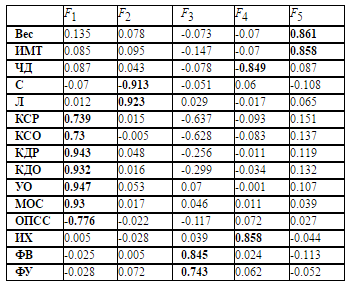
Таблица 2. Факторная структура на базе нейронной сети («варимакс» критерий)

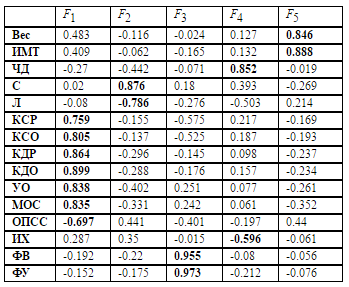
Таблица 3. Факторная структура на базе нейронной сети (критерий интерпретируемости)

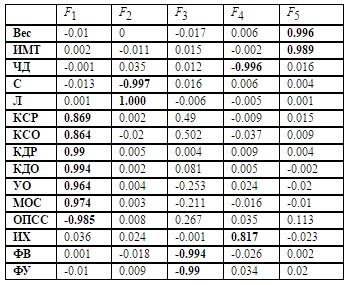
Специальный критерий интерпретируемости оказался более эффективным, чем «варимакс» критерий. Разделение исходных переменных на факторы более мощное: незначимые факторные нагрузки близки к 0, тогда как значимые близки к 1. Незначимые факторные нагрузки отдают свою долю дисперсии переменных, приходящиеся на факторы, значимым фактоным нагрузкам, тем самым повышая эффективность разбиения исходных параметров на факторы. Конечным этапом факторного моделирования является интерпретация наполнения факторов переменными и более эффективное разбиение исходных переменных на факторы, соответствующее целям классического факторного вращения, является плюсом факторного моделирования на базе нейронной сети со специальным критерием интерпретируемости. Расхождение величин незначимых факторных нагрузок матриц факторного отображения до и после факторного вращения является обычным эффектом, целью которого является повышение эффективности интерпретационного разделения исходных переменных на факторы.

Матрица корреляций факторов немного отличается от ортогональной, что соответствует общему косоугольному случаю (таблица 4).

Таблица 4.Корреляции факторов, полученных на базе нейронной сети

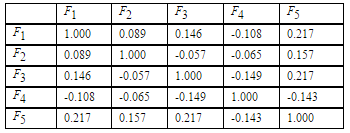
с использованием критерия интерпретируемости

Факторное моделирование позволяет выделить группы взаимосвязанных параметров, образующих факторы заболевания артериальной гипертензии. Факторы проинтерпретированы в ранних работах[13, 14]:

1. Главный фактор можно интерпретировать как гемодинамический фактор, включающий параметры, описывающие центральную и периферическую гемодинамику. Переменные УО, МОС, ОПСС определяют уровень артериального давления. В норме, изменениям минутного объема циркуляции должна соответствовать адекватная по величине и направлению реакция прекапиллярного русла, которая бы нивелировала эти изменения и сохраняла среднее давление на нормальном уровне. Например, если МО снижен, то артериолы должны сузиться. Если МО увеличен, то артериолы должны расшириться. Нарушения взаимосвязи этих показателей лежат в основе изменений уровня АД. Вместе с тем изменение уровня артериального давления взаимосвязано с модуляцией сердца, за которую отвечают параметры КСР, КСО, КДР, КДО.

2. Фактор составленный из параметров Фракция выброса левого желудочка и Фракция укорочения ЛЖ можно считать важным для непосредственной оценки контрактильной (сократительной, нагнетательной) функции левого желудочка. Этот фактор определяет объемную ресурсоемкость ЛЖ. Он показывает, насколько использованы объемные резервы самого сердца для поддержания уровня артериального давления.

3. Фактор, отвечающий за соответствие массы и роста.

4. Фактор, характеризующий уровень слаженности работы сердца и легких, определяется через частоту дыхания и индекс Хильдебранта.

5. Иммунологический фактор, который может отражать психосоматическое состояние индивида, поскольку этот фактор активируется в стрессовых состояниях. Основной вклад в формирования этого фактора вносят сегментоядерные нейтрофилы и лимфоциты.

Выделенные факторы являются различными аспектами заболевания. Например, это может быть такой фактор риска как ожирение и нарушение фактора 3. Факторы 4 и 5 соответствуют стрессовой восприимчивости, при которой нарушается иммунологический фактор и фактор слаженности работы сердца и легких. Все выделенные факторы подтверждены независимыми медицинскими исследованиями.

В ранней работе [13] даны рекомендации по&

© Habrahabr.ru