Ёжик во фрактальном тумане
Эта статья — последняя из серии моих хабрастатей о фракталах. В хабрастатье «Рисуем картинки с помощью кривой Гильберта» рассказывалось о котёнке по имени Гав, в хабрастатье «Кош на комплексной плоскости» — о перетекании фракталами в горизонт, в хабрастатье «Ночь фракталов» — об алгоритме времени убегания. В этой статье пойдёт речь о ёжике в тумане и, конечно же, о коте.
Каждый, кто хоть чуток сталкивался с фракталами, видел красивые картинки множеств Жюлиа, которые определяются квадратным многочленом;, но интересно решать обратную задачу: пусть есть некоторая картинка, а мы ходим по ней придумать такой многочлен, который даст некоторое приближение исходной картинки. Картинка с ёжиком выше демонстрирует эту идею.
Итак, рассмотрим кота K.
Нам нужно придумать такой многочлен f, чтобы внутри кота последовательность f (z), f (f (z)), f (f (f (z))), … была ограниченной, а вне кота — стремилась к бесконечности. Долго над этим вопросом я не думал, а сразу же поискал в интернете и нашёл замечательную статью Kathryn A. Lindsey, «Shapes of polynomial Julia sets», 2013, arXiv:1209.0143. В этой статье доказывается что для «хорошего» кота и для заданной точности δ такой многочлен придумать можно, причём доказательство конструктивно.
Рассмотрим эту конструкцию. Пусть φ' — конформное отображение, которое внешность единичной окружности переводит во внешность кота. Пусть φ (z) = φ'((1 + ε)z) — подправленное на некоторое малое ε исходное отображение.
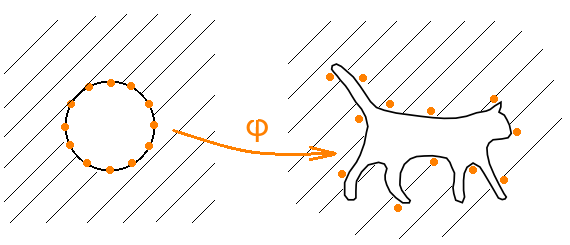
Далее, пусть ω (z) = c−n (z − r0)(z − r1) ⋅… ⋅ (z − rn−1), где c — коэффициент при z в разложении отображения φ в ряд Лорана, а rk = φ (e2πik/n) — образы корней из единицы n-ой степени. Доказывается, что многочлен f (z) = z (ω (z) + 1) будет искомым при достаточно большом n.
Следовательно, для решения нашей задачи необходимо научиться генерировать соответствующее конформное отображение. В результате небольшого поиска в интернете, был найден пакет zipper. Этот пакет позволяет находить конформное отображение внутренности единичного круга на область, ограниченную ломаной. Хотя этот пакет написал лет двадцать назад на древнем наречии, собрать его и воспользоваться им не составило труда.
Кусочек на древнем наречии call invers write (4,*)z1, z2, z3, zrot1, zto0, zto1, angler, zrot2 do 981 j=4, n-2,2 981 write (4,999)a (j), b (j), c (j) zm=dcmplx (0.d0,0.d0) ierr=0 do 982 j=1, n if (cdabs (zm-z (j)).lt.1.d-16)then ierr=1 jm=j-1 write (*,*)' WARNING: prevertices', j,' and', jm,' are equal' endif zm=z (j) x=dreal (z (j)) y=dimag (z (j)) 982 write (3,999)x, y if (ierr.eq.1)then Обмазываем zipper клеем на питоне def calc_phi (points): with open («init.dat», «w») as output_file: for point in points: output_file.write (str (point.real) + » » + str (point.imag) + »\n») output_file.write (»\n0.0 0.0\n») os.system («echo \«init.dat\n200\npoly.dat\» | ./polygon») os.system (»./zipper») os.system («rm init.dat»)
def transform_points (points):
with open («fftpts.dat», «w») as output_file:
for point in points:
output_file.write (str (point.real) + » » + str (point.imag) + »\n»)
os.system («echo \»0\nfftpts.dat\nfftpts.img\n0\» | ./forward»)
transformed_points = []
with open («fftpts.img», «r») as input_file:
for line in input_file.readlines ():
x, y = float (line[0:25]), float (line[25:])
transformed_points.append (complex (x, y))
os.system («rm fftpts.dat»)
os.system («rm fftpts.img»)
return transformed_points
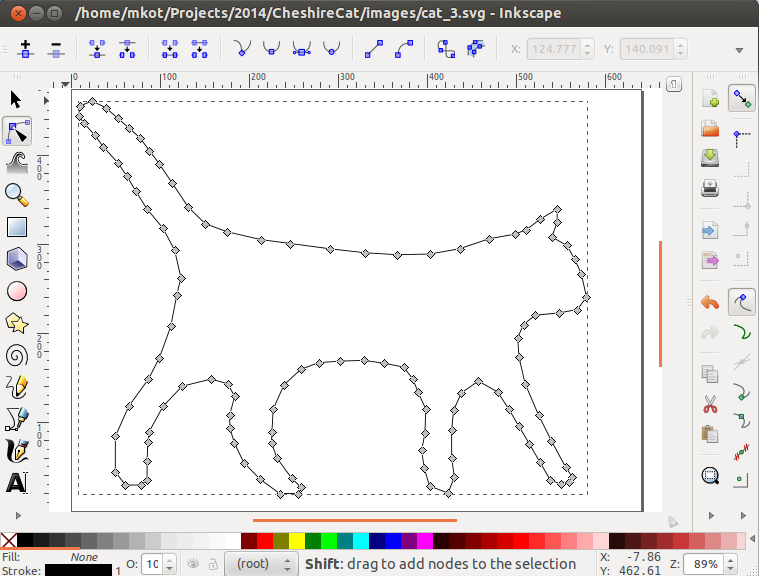
Чтобы использовать этот пакет, нужно по изображению построить ломаную. Я не стал делать какого-то автоматического решения, а загрузил изображение в редактор Inkscape и обвёл его, а распарсить SVG-формат проще простого. Это удобно тем, что позволяет экспериментировать с ломаной.Парсим пути в SVG-файле
def read_points_from_svg (file_name, path_n):
with open (file_name, «r») as input_file:
content = input_file.read ()
soup = BeautifulSoup.BeautifulSoup (content)
path = soup.findAll («path»)[path_n]
data = path.get («d»).split (» »)
x, y = 0, 0
is_move_to = False
is_relative = False
points = []
for d in data:
if d == «m»:
is_move_to = True
is_relative = True
elif d == «M»:
is_move_to = True
is_relative = False
elif d == «z»:
pass
elif d == «Z»:
pass
elif d == «l»:
is_move_to = False
is_relative = True
elif d == «L»:
is_move_to = False
is_relative = False
else:
dx, dy = d.split (»,»)
dx = float (dx)
dy = float (dy)
if is_move_to:
x = dx
y = dy
is_move_to = False
else:
if is_relative:
x += dx
y += dy
else:
x = dx
y = dy
points.append (complex (x, y))
return points
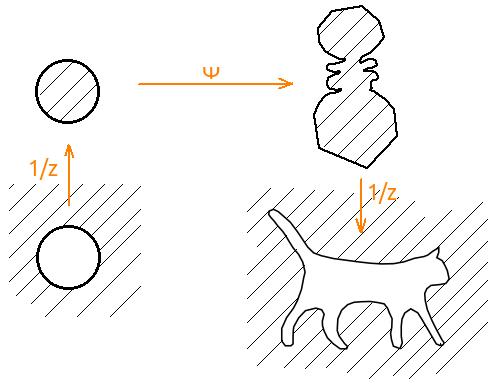
Далее, нам нужно отображение из внешности во внешность, а пакет находит отображение из внутренности во внутренность. Здесь нужно просто сопрячь генерируемое отображение инверсией. То есть φ'(z) = 1 / ψ (1/z), где ψ — отображение, которое генерирует пакет. А на вход пакета надо подавать уже инвертированную ломанную.
Сопрягаем def invert_points_1(points, epsilon): inverted_points = [] for point in points: inverted_points.append (1 / ((1 + epsilon)*point)) return inverted_points
def invert_points_2(points, shift): inverted_points = [] for point in points: inverted_points.append (1 / point + shift) return inverted_points
if __name__ == »__main__»:
…
inverted_points = invert_points_1(points, epsilon)
transformed_points = transform_points (inverted_points)
inverted_transformed_points = invert_points_2(transformed_points, shift)
В определении многочлена f ещё участвует коэффициент c. Для приближённого вычисления его значения воспользуемся следующим приёмом. Пусть
f (z) = cz + a + a1/z + a2/z2 + a3/z3 +…
Рассмотрим некоторую конечную, но достаточно большую, часть этого ряда. Подставим в ряд значения корней из единицы n-ой степени, где n больше числа членов этого куска.
f (e2πik/n) = ce2πik/n + a + a1e−2πik/n + a2e−4πik/n + a3e−6πik/n + …, k = 0, …, n − 1.
Теперь умножим каждую строку на e−2πik/n и сложим все строки. Так как сумма всех корней из единицы равна 0, то справа останется только nc. Поэтому можно положить
c = (f (1) ⋅ 1 + f (e2πi/n)e−2πi/n +… + f (e2πi (n − 1)/n)e−2πi (n − 1)/n)) / n.
Соберём всё вместе и проверим, что получилось. На рисунке ниже приведён «тепловой» график логарифма модуля f (z) (чем краснее, тем больше значение). Как видно, внутри кота значения многочлена маленькие, а вне кота многочлен возрастает, так и должно быть. Заметьте также, как распределяются значения f (e2πik/n) (зелёные точки), из-за этого эффекта пришлось рисовать кота, у которого ноги достаточно далеко находятся друг от друга.
Теперь просто-напросто применяем какой-нибудь алгоритм для рисования множества Жюлиа и получаем кота, граница которого фрактальна.
Например, алгоритм времени убегания def get_value (points, z, radius): result = 1 for point in points: result *= (z — point) / radius return z * (1 + result)
def get_radius (points): n = len (points) result = 0 for k in range (n): result += points[k] * cmath.exp (-2j*math.pi*k/n) return result / n
def draw_fractal (image, points, scale, shift, bound, max_num_iter, radius):
width, height = image.size
draw = ImageDraw.Draw (image)
for y in range (0, height):
for x in range (0, width):
z = (complex (x, y) — shift) * scale
n = 0
while abs (z) < bound and n < max_num_iter:
z = get_value(points, z, radius)
n += 1
if n < max_num_iter:
color = ((100 * n) % 255, 128 + (50 * n) % 255, 128 + (75 * n) % 255)
draw.point((x, y), color)
Если же у нас изображение состоит из нескольких областей A1, A2, …, Aq, то в вышеупомянутой статье предлагается использовать вместо многочлена рациональное отображение f (z), определённое следующим образом. Для каждой области Ar, запишем произведение ωr (z) как сделано выше. Тогда искомая рациональная функция f (z) определяется формулой f (z) = z / (1/ ω1(z) +… + 1 / ωq (z)).
Например, пусть у нас есть ёжик в тумане Ё.
Обведём ёжика и холм (нижняя граница холма находится за пределами картинки).
Ёжик в вакууме.
Холм без ёжика.
Всё вместе.
Увеличенное брюхо ёжика с блохами-ежами.
Как всегда, исходный код можно найти на гитхабе.
Ещё раз повторю ссылку на статью, с помощью которой всё получилось: Kathryn A. Lindsey, «Shapes of polynomial Julia sets», 2013, arXiv:1209.0143. Отмечу, статья легко читается, так что можете поразбирать доказательства за чашкой чая.
Надеюсь было весело.
Неудавшиеся дубли
