Есть проблемы гораздо сложнее, чем NP-Complete06.06.2023 11:16

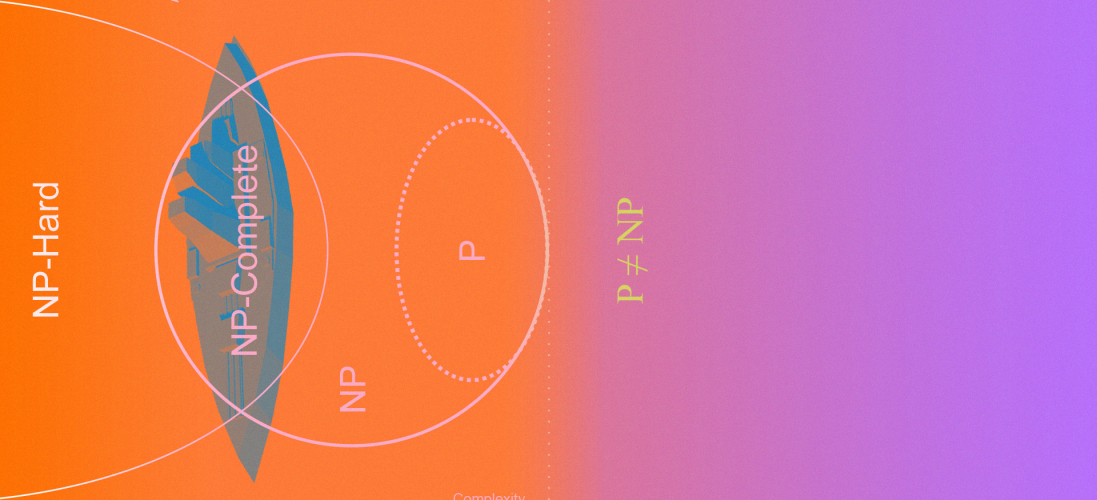
Люди часто сравнивают P и NP в таком духе, что проблемы P простые, а NP — сложные. Но это чрезмерное упрощение. На самом деле проблемы могут быть намного, намного сложнее, чем NP.

В этом смысле можно вспомнить интеллектуально-фантастический триллер Travelling Salesman (Коммивояжёр, 2012) о четырёх математиках, нанятых правительством США для решения самой сложной проблемы в истории информатики — равенства классов сложности P и NP (P versus NP problem). И им это удалось. Чиновник министерства обороны США предлагает за их алгоритм вознаграждение $10 млн. Но сами математики слишком хорошо понимают, какие разрушительные последствия принесёт в мир их открытие. Один из лучших фильмов про математику в истории кинематографа…

Здесь и далее — кадры из фильма Travelling Salesman (2012)

Алгоритм быстрого поиска кратчайшего маршрута коммивояжёра, если он будет найден, может быть преобразован в быстрые алгоритмы для решения других задач, таких как разложение больших чисел на множители. Системы шифрования будут скомпрометированы, это позволит получить доступ к личным данным, к личной переписке, банковским счетам и, возможно, к государственным секретам.

Проблема равенства классов сложности P и NP, также известная как проблема перебора, является одной из семи задач тысячелетия, за решение которой Математический институт Клэя назначил премию в миллион долларов США.

❯ Краткая история вопроса

P — от английского polynomial, NP — от английского non-deterministic polynomial. Для полноты изложения: ещё есть NPC — non-deterministic polynomial complete, или NP-полные задачи. Классификация задач в теории сложности многократно расширялась и дополнялась.

Задача коммивояжёра — частый пример математической проблемы классов сложности P и NP, задача быстрого поиска кратчайшего маршрута коммивояжера (Travelling salesman problem, TSP). Есть конечный набор городов с расстояниями между ними. Необходимо найти упорядоченный набор этих городов, в котором был бы кратчайший путь обхода всех городов без повторного посещения.

Решение задачи для пяти городов требует рассмотрения 5! вариантов.

Если количество городов возрастает 50, то количество вариантов равно 30414093201713378043612608166064768844377641568960512000000000000. У фантастического компьютера с производительностью 100 эксафлопс требуемое время расчёта перебором составит ~3•1044сек или 1036лет!

Для понимания, время существования нашей Вселенной оценивается примерно в 1010лет.

Неужели для поиска оптимального пути нет способа найти кратчайший путь, не просматривая их все? До сих пор нет алгоритма, кроме тех, которые по сути — перебор всех путей.

Что «насущно» или прикладной аспект:

Криптосистема с открытым ключом (несимметричная) строится на реализации односторонних функций и вычислительной сложности решения задач: легко создать пару из открытого ключ и закрытого ключа, быстро зашифровать открытым ключом, быстро расшифровать, используя закрытый ключ, но вычислительно сложно, имея открытый ключ, восстановить закрытый ключ или, получив доступ к открытому ключу и зашифрованному сообщению, восстановить исходное сообщение.

Односторонняя функция. Суть идеи для защиты систем от злоупотребления предоставляемыми сервисами — асимметрия временных затрат: запрашивающая сторона решает задачу, которая требует значительное время на нахождение решения и мало времени для проверки результата.

Клиентская головоломка (client puzzle) или вычислительная головоломка (computational puzzle). Не следует путать с защитными капчами, которые легки для человека, но трудны или неразрешимы для компьютера.

Цитата из работы 1992 года «Pricing via Processing or Combatting Junk Mail» исследователей из IBM докторов Синтии Дворк (Cynthia Dwork) и Мони Наор (Moni Naor): «Основная идея заключается в том, чтобы потребовать от пользователя умеренно сложных вычислений (но не трудноразрешимых) для доступа к ресурсу, тем самым предотвращая злонамеренное использование».[1]

Тогда они ещё не использовали термин «доказательство работы» (proof-of-work), который позже станет общепринятым, когда получат реализацию блокчейны.

В 1997 году криптограф Адам Бэк (Adam Back) предложил другую идею [3] — использовать не криптографические головоломки как у Синтии Дворк и Мони Наор, а выборочные хеши: которые можно произвольно сделать сложными для вычисления, но которые можно быстро проверить. Его система Hashcash применяется для противодействия спаму и DoS-атакам. Позже система Hashcash стала использоваться в Bitcoin и других криптовалютах.

Доказательство выполнения работы. В 1999 Маркус Якобссон (Markus Jakobsson) и Ари Джуелс (Ari Juels) в статье «Proofs of Work and Bread Pudding Protocols» опубликованной в журнале «Communications and Multimedia Security» стали использовать название — Proof-of-Work, PoW [2].

Хэл Финни (Hal Finney) 6 августа 2004 года в письме на форуме шифропанков предложил использование многоразового доказательства выполнения работы (reusable proof-of-work, RPOW, RPoW) для организации электронной валюты. Как мы знаем, именно Финни стал получателем первой транзакции 12 января 2009 года в 10 BTC от создателя биткоина Сатоши Накамото.

Сатоши Накамото использовал PoW для реализации алгоритмов биткоина, взял Hashcash, добавил механизм изменяющейся сложности — уменьшение или увеличение требуемого числа нулей в зависимости от суммарной мощности участников сети, сложность вычислений для добавления нового блока в биткоин стала динамическим параметром, которая устанавливается на таком уровне, чтобы скорость генерации блоков оставалась на одном уровне вне зависимости от оборудования участников. А для проверки корректности уже сформированного блока требуется лишь однократное вычисление хеша. Вычисляемая функция — SHA-256.

❯ Семь задач тысячелетия

• Равенство классов P и NP
• Гипотеза Ходжа
• Гипотеза Пуанкаре (решена)
• Гипотеза Римана
• Квантовая теория Янга — Миллса
• Существование и гладкость решений уравнений Навье — Стокса
• Гипотеза Бёрча — Свиннертон-Дайера

Если будет доказано равенство классов P и NP, это будет означать, что теоретически возможно решать многие сложные задачи существенно быстрее, чем сейчас. В прикладном аспекте: если задачи, для которых, как считалось, не существует эффективных алгоритмов, получат быстрые решения, то многие методы защиты устареют.

Кадр из фильма Travelling Salesman

История проблемы равенства классов сложности P и NP

Первое упоминание проблема равенства классов было в 1956 году — в письме Курта Гёделя (Kurt Friedrich Gödel) Джону фон Нейману (John von Neumann). До восьмидесятых годов XX века о письме не было известно. Первые научные публикации появились в начале семидесятых, проблема математически была сформулирована к 1971 году.

Стивен Кук (Stephen Arthur Cook) и Леонид Левин (Leonid Levin) сформулировали проблему независимо друг от друга. Ричард Карп (Richard Karp) опубликовал в 1972 году в работе «Сводимость комбинаторных задач» («Reducibility Among Combinatorial Problems») [4].

❯ Задачи посложнее, чем NP-полные

В теории сложности вычислений NP-трудность — недетерминированная полиномиальная трудность по времени является определяющим свойством класса задач, которые, по крайней мере, так же сложны, как самые сложные задачи в NP. Простой пример NP-трудности — задача о сумме подмножеств. [12]

Класс сложности PSPACE (PSPACE-complete)

Это набор всех проблем разрешимости, которые могут быть решены машиной Тьюринга с полиномиальным ограничением пространства.

Предполагается, но не доказано, что PSPACE строго больше, чем NP. Другими словами, для решения некоторых задач требуется полиномиальное пространство, но неполиномиальное время для проверки.

PSPACE это сокращение — Polynomial Space.

Как следствие из теоремы Сэвича [13], NPSPACE эквивалентен PSPACE, и детерминированная машина Тьюринга может моделировать недетерминированную машину Тьюринга, не занимая существенно больше места, но может использовать существенно больше времени. Недетерминированная машина Тьюринга не добавляет никакой дополнительной мощности.

Класс сложности EXPTIME (EXPTIME-complete)

Это множество задач, решаемых детерминированной машиной Тьюринга за экспоненциальное время O (2p (n)), где p (n) — это полиномиальная функция от n, т. е. сложность растёт с O (2^n). Есть мнение, что EXPTIME строго больше, чем PSPACE и NP, а это означает, что есть проблемы, для решения которых требуется больше, чем полиномиальное пространство, и больше, чем полиномиальное время, для проверки.

Пример — обобщение игр: го, шахматы, шашки, где доска может быть любого размера.

Класс сложности 2- EXPTIME (2-EXPTIME-complete)

Похож на EXPTIME, за исключением того, что вместо O (2^n), здесь у нас O (2^(2^n)), решаемый детерминированной машиной Тьюринга. Многие нишевые и необычные проблемы подпадают под 2-EXPTIME. Пример — решение арифметических выражений Пресбургера (Presburger) [7].

Класс сложности ELEMENTARY (ELEMENTARY-complete), начальный

Это EXPTIME, 2-EXPTIME, 3-EXPTIME и т. д. Название классу сложности дал Ласло Калмар (Laszlo Kalmar) в контексте рекурсивных функций [14]. Если задача элементарная, значит, есть какое-то n, где задача строго в n-EXPTIME. Но вероятно, ELEMENTARY-complete задач не бывает. Для каждой элементарной задачи существует более сложная элементарная задача.

Класс сложности TOWER (TOWER-complete)

Определим тетрацию (tetration) ^^ как многократное возведение в степень, поэтому 3^^2 = 3^3, 3^^3 = 3^(3^3) и т.д. Таким образом, TOWER-complete является O (2^^n). В конечном итоге, каждое 2^^n превращается в экспоненциальную «башню» [8].

Класс сложности Ackermann-complete. Функция Аккермана

Вариант функции Аккермана: A (1) = 1×1, A (2) = 2^2, A (3) = 3^^3, A (4) = 4^^^4 и т. д.

Функция Аккермана — простейший пример корректно определённой функции, которая является вычислимой, но не примитивно-рекурсивной.

Задачи, полные по Вильгельму Аккерману (Wilhelm Ackermann), требуют времени, растущего с O (A (n)) [9].

Класс сложности Hyperackermann-complete

В публикации «Иерархии сложности за пределами элементарного» вводится класс сложности Hyperackermann и приводятся его примеры [10].

Как говорится, математика правит миром. Да пребудет с вами сила!

❯ Литература

1. Dwork, C. and Naor, M. (1992) Pricing via Processing or Combatting Junk Mail. In: Brickell, E.F., Ed., Advances in Cryptology—CRYPTO»92, Springer, Berlin, 139–147. doi.org/10.1007/3–540–48071–4_10
2. Jakobsson, Markus; Juels, Ari (1999). «Proofs of Work and Bread
   Pudding Protocols». Secure Information Networks: Communications and Multimedia Security. Kluwer Academic Publishers: 258–272. doi:10.1007/978–0–387–35568–9_18.
3. Back, Adam. «HashCash». A popular PoW system. First announced in March 1997.
4. Karp, Richard M. (1972). «Reducibility Among Combinatorial Problems» (PDF). In R.E. Miller; J.W. Thatcher; J.D. Bohlinger (eds.). Complexity of Computer Computations. New York: Plenum. pp. 85–103. doi:10.1007/978–1–4684–2001–2_9. ISBN 978–1–4684–2003–6.
5. Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман. Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: «Вильямс», 2002. — 528 с. — ISBN 0–201–44124–1.
6. Hopcroft, Motwani, Ullman: «Introduction to Automata Theory, Languages, and Computation»
7. Fischer, M. J., and Michael O. Rabin, 1974, «Super-Exponential Complexity of Presburger Arithmetic. Archived 2006–09–15 at the Wayback Machine» Proceedings of the SIAM-AMS Symposium in Applied Mathematics Vol. 7: 27–41
8. TOWER-complete problems in contraction-free substructural logics. Hiromi Tanaka
9. Ackermann, Wilhelm (1928). «Zum Hilbertschen Aufbau der reellen Zahlen». Mathematische Annalen. 99: 118–133. doi:10.1007/BF01459088. S2CID 123431274
10. Complexity Hierarchies Beyond Elementary, Sylvain Schmitz
11. Problems harder than NP-Complete
12. Knuth, Donald (1974). «Postscript about NP-hard problems». ACM SIGACT News. 6 (2): 15—16. DOI:10.1145/1008304.1008305
13. W.J. Savitch, «Relationship between nondeterministic and deterministic tape classes», J.CSS, 4, pp 177—192, 1970
14. Rose H. E… Subrecursion. Functions and hierarchies. Oxford logic guides, no. 9. Clarendon Press, Oxford University Press, Oxford and New York 1984, xiii + 191 pp., June 2014, Journal of Symbolic Logic 52(02):563–565. DOI:10.2307/2274410

© Habrahabr.ru