Есть ли параллелизм в произвольном алгоритме и как его использовать лучшим образом
Параллелизации обработки данных в настоящее время применяется в основном для сокращения времени вычислений путем одновременной обработки данных по частям на множестве различных вычислительных устройств с последующим объединением полученных результатов. Параллельное выполнение позволяет «обойти» сформулированный лордом Рэлеем в 1871 г. фундаментальный закон, согласно которому (в применимости к тепловыделению процессоров) мощность их тепловыделения пропорциональна четвертой степени тактовой частоты процессора (увеличение частоты вдвое повышает тепловыделение в 16 раз) и фактически заменить его линейным от числа параллельных вычислителей — при сохранении тактовой частоты). Ничто не дается даром — задача выявления (обычно скрытого для непосвящённого наблюдателя, [1]) потенциала параллелизма в алгоритмах не является лежащей на поверхности, а уж эффективность его (параллелизма) использования — тем более.
Ниже приведена иллюстрация процесса выявления параллелизма для простейшего случая вычисления выражения axb+a/c (a, b, c — входные данные).
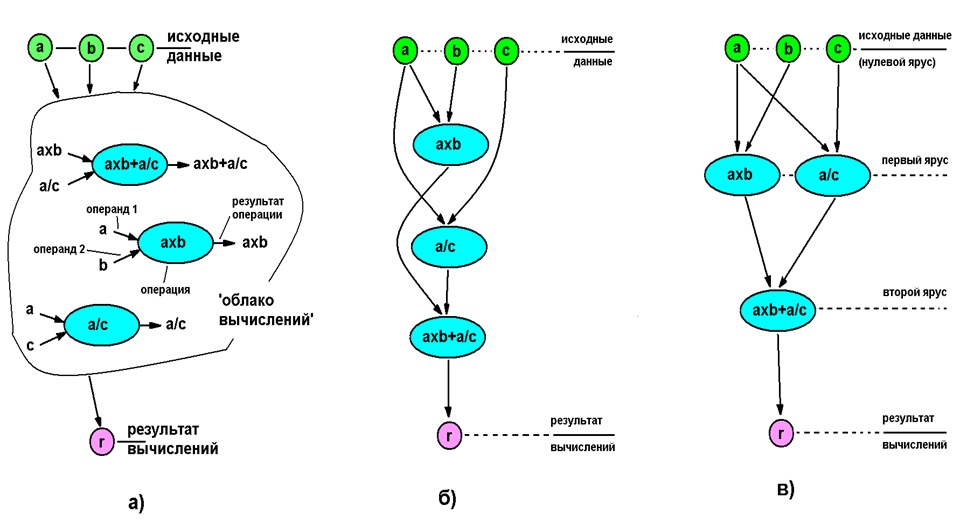
а) — «облако операторов» (последовательность выполнения не определена), б) — полностью последовательное выполнение, не определена), б) — полностью последовательное выполнение, в) — параллельное исполнение
Даже в таком примитивном алгоритме параллельное выполнение ускорило вычисления в полтора раза, но потребовало двух вычислителей вместо одного. Обычно с увеличением числа операторов (усложнением алгоритма) ускорение вычислений возрастает (хотя имеются и полностью нераспараллеливаемые на уровне арифметических действий алгоритмы — напр., вычисление чисел Фибоначчи). Для приведенного на рис. 1 алгоритма все выкладки легко выполняются «в уме», но для реальных (много более сложных алгоритмов) требуется машинная обработка.
Параллельная вычислительная система включает несколько вычислителей (арифметико-логических устройств), объединённых общей или локальной оперативной памятями и кэшами. Современные параллельные системы часто имеют не только гомогенное, но и гетерогенное вычислительное поле. Задача распределения вычислений между отдельными вычислителями приводит к разработке расписания (плана) вычислений. Проблемой является многозначность расписаний параллельного выполнения алгоритма в общем случае это NP-полная задача [2], точное решение (при заданных оптимизационных требованиях) которой можно получить только методом полного перебора (что нереально при числе операторов уже более сотен-тысяч). Выходом является использование эвристических методов, исходя из сложности данную область знания можно обоснованно отнести к наиболее сложным случаям «Науки о данных» (Data Science).
Параметрам выполнения распространенных алгоритмов в параллельном варианте посвящен известный ресурс AlgoWiki [3].
Особенно интересен, с точки зрения автора, вариант параллелизации для языков программирования высокого уровня без явного указания распараллеливания и в системах c концепцией ILP (Instruction-Level Parallelism, параллелизм на уровне команд, с реализацией посредством вычислительной архитектуры EPIC (Explicitly Parallel Instruction Computing, явный параллелизм выполнения команд). При этом аппаратное обеспечение вычислительных систем сильно упрощается и все проблемы выявления параллелизма и построение собственно расписания выполнения программы для заданной конфигурации параллельной вычислительной системы ложатся на компилятор, что ведет к его усложнению и снижению скорости компиляции.
Одним из эффективных способов решения задачи определения рациональных планов выполнения параллельной задачи является представление алгоритма в виде графа с последующей его (графа) обработкой (при этом собственно граф остается неизменным, а меняется лишь его представление). Часто применяется Информационный Граф Алгоритма (ИГА). ИГА отображает зависимость вида «операторы — операнды», при этом вершины графа ассоциируются с операторами (группами операторов) программы, а дуги — с линиями передачи (хранения) данных). ИГА обладает свойствами направленности, ацикличности и параметризован по размеру обрабатываемых данных (из-за последнего приходится исследовать один и тот же алгоритм с конкретным набором исходных данных).
Одной из важных процедур выявления параллелизма по заданному ИГА является получения его исходной (обладающей свойством каноничности) Ярусно-Параллельной Формы (ЯПФ), [4]. При этом условием расположением операторов на едином ярусе является независимость их друг от друга по информационным связям (необходимое условие их параллельного выполнения).
Получение такой (без условия ограниченности количества операторов на ярусах) ЯПФ требует O (N2) действий, где N — число операторов (вершин графа), ее высота (общее число ярусов) равна увеличенной на единицу длине критического пути в ИГА. Напрямую использовать такую ЯПФ в качестве основы для построения расписания выполнения параллельной программы обычно затруднительно (ширина некоторых ярусов часто сильно превышает число имеющихся параллельных вычислителей). Но т.к. вычисление такой ЯПФ вычислительно малозатратно, во многих случаях целесообразно начинать анализ именно с ее получения и в дальнейшем проводить модификацию этой ЯПФ с учетом конкретных задач. При этом при каждой модификации ЯПФ получаем новую форму, полностью соответствующую исходному ИГА.
Определенным недостатком использования метода построения ЯПФ для получения расписания является невозможность учета времени исполнения операторов, однако для современных микроархитектур характерно всемерное стремление к одинаковости времен выполнения всех операторов, что как раз повышает удобство использования ЯПФ.
На рис. ниже приведен несложный случай алгоритма вычисления вещественных корней полного квадратного уравнения ax2+bx+c=0.
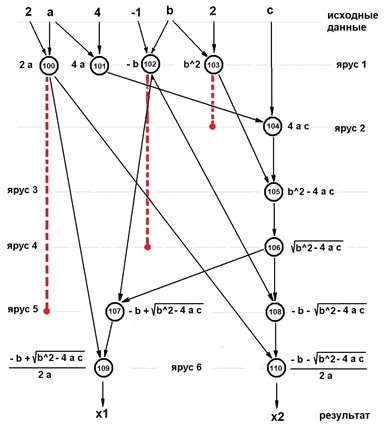На рисунке — ярусно-параллельная форма алгоритма решения полного квадратного уравнения в вещественных числах в канонической форме (номера ярусов ЯПФ расположены справа)
Показанная ЯПФ уже является расписание выполнения параллельной программы (выполнение начинается «сверху вниз», требует 6 относительных единиц времени и 4-х параллельных вычислителей). При этом число задействованных вычислителей по ярусам крайне неравномерно (важно при однозадачном режиме работы вычислительной системы) — на 1-м ярусе задействованы все 4, на 2,3,4 — только один и по два на 5- и 6 ярусах. Однако легко видеть, что простейшее преобразование (показанные красным пунктиром допустимые перестановки операторов с яруса на ярус) позволяют выполнить тот же алгоритм за то же (минимальное из возможных) время всего на двух вычислителях! Не для любого алгоритма получается столь идеально — часто для снижения требуемого числа параллельных вычислителей единственным путем является увеличение времени выполнения алгоритма (возрастание числа ярусов ЯПФ).
Для решения задач определения рационального (на основе заданных критериев) расписания выполнения произвольных алгоритмов создан инструментальный программный комплекс, включающая два модуля — D-F и SPF@home. Свободная выгрузка инсталляционных файлов доступна с ресурсов http://vbakanov.ru/dataflow/content/installdf.exe и http://vbakanov.ru/spf@home/content/installspf.exe соответственно (дополнительная информация по теме — http://vbakanov.ru/dataflow/dataflow.htm и http://vbakanov.ru/spf@home/spf@home.htm).
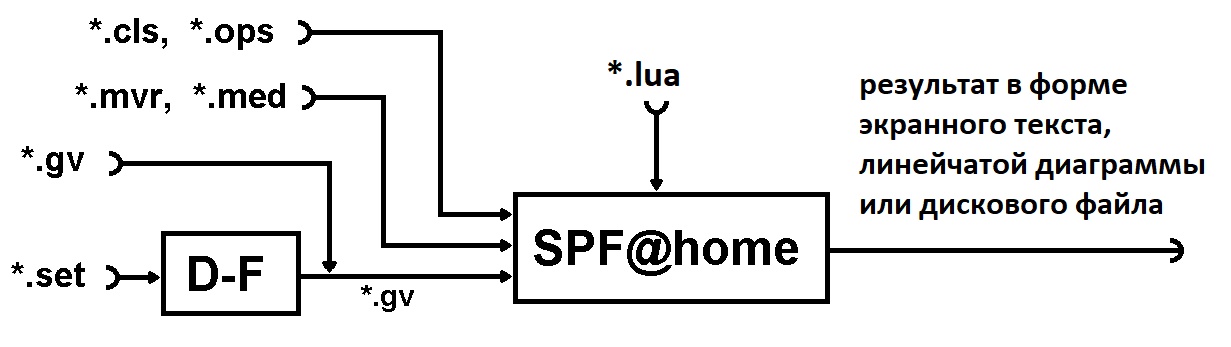На рисунке — схема инструментального комплекса (*.set и *.gv — программный файл и файл информационного графа анализируемой программы соответственно, *.mvr, *.med — файлы метрик вершин и дуг графа алгоритма соответственно, *.cls, *.ops — файлы параметров вычислителей и операторов программы соответственно, *.lua — текстовый файл на языке Lua, содержащий методы реорганизации
На вход комплекса поступает описание анализируемого алгоритма в форме традиционной программы (set-файлы) или формального описания в виде ориентированного ациклического информационного графа алгоритма — ИГА в форме gv-файов (зависимость вида «операторы — операнды», при этом вершины графа ассоциируются с операторами (группами операторов) программы, а дуги — с линиями передачи (хранения) данных). ИГА обладает свойствами направленности, ацикличности и параметризован по размеру обрабатываемых данных (из-за последнего приходится исследовать один и тот же алгоритм с конкретным набором исходных данных).
В данном случае исследования по разработке и совершенствованию методов решения вопроса создания эффективных эвристик генерации обобщенного расписания (каркаса) выполнения параллельных программ проводились с помощью нижеописанного специализированного программного комплекса. Термин «каркас» здесь обоснован вследствие абстрагирования в данной работе от конкретных технологий параллельного программирования.
Для управления созданием расписания используется встроенный скриптовый язык Lua (Lua написан на ANSI C, обеспечивает неявную динамическую типизацию, поддерживает прототипную модель объектно-ориентированного программирования и был выбран на основе свойств его компактности, полной открытости исходных кодов и близости синтаксиса к распространенному С).
Родительское приложение создано с использованием языка программирования С++, является GUI Win»32-программой и доступно для свободной выгрузки и использования (как и исходные тексты) через GIT-репозиторий. Вывод данных осуществляется на экран в текстовом и графическом форматах и в файлы (также в структурированной текстовой форме).
Сочетание компилируемой родительской программы и встроенного интерпретатора скриптового языка позволило обеспечить высокую производительность и гибкость (Lua-вызовы фактически являются «обертками» для API-функций модуля SPF@home).
Копии экранов обсуждаемого комплекса приведены на изображениях ниже (программные модули D-F и SPF@home соответственно).
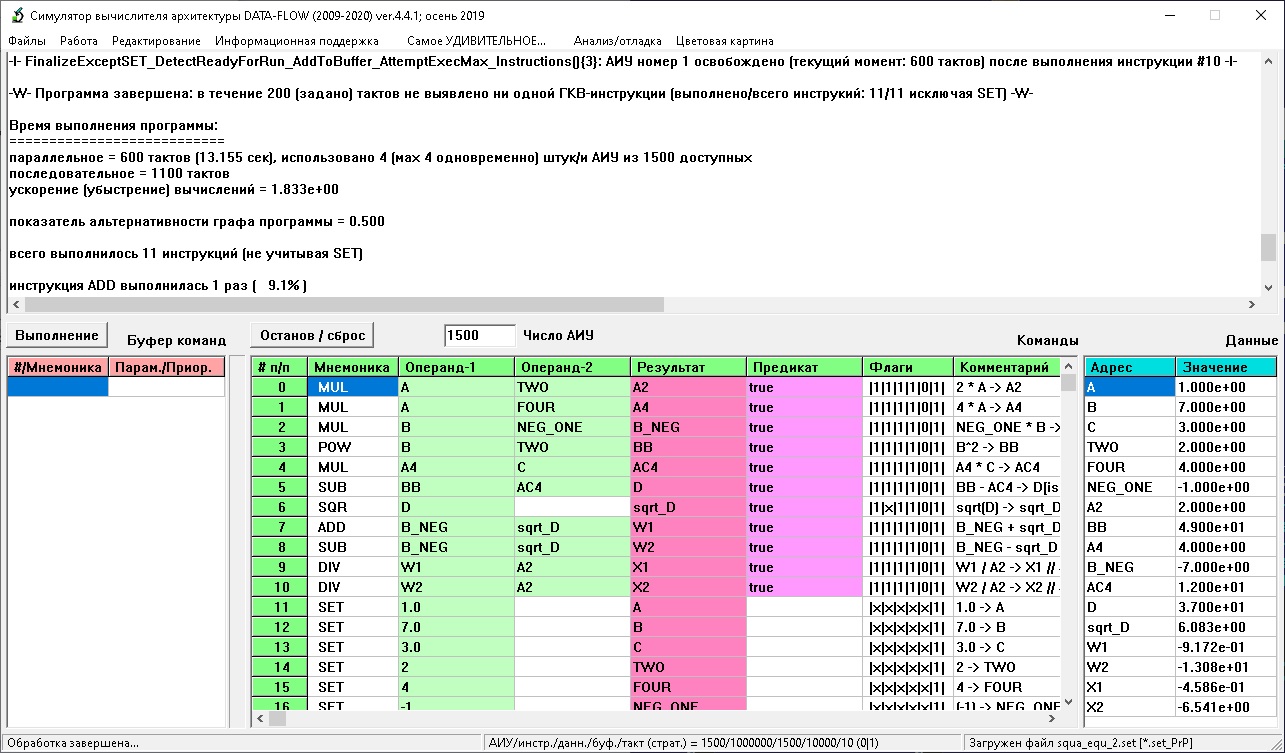
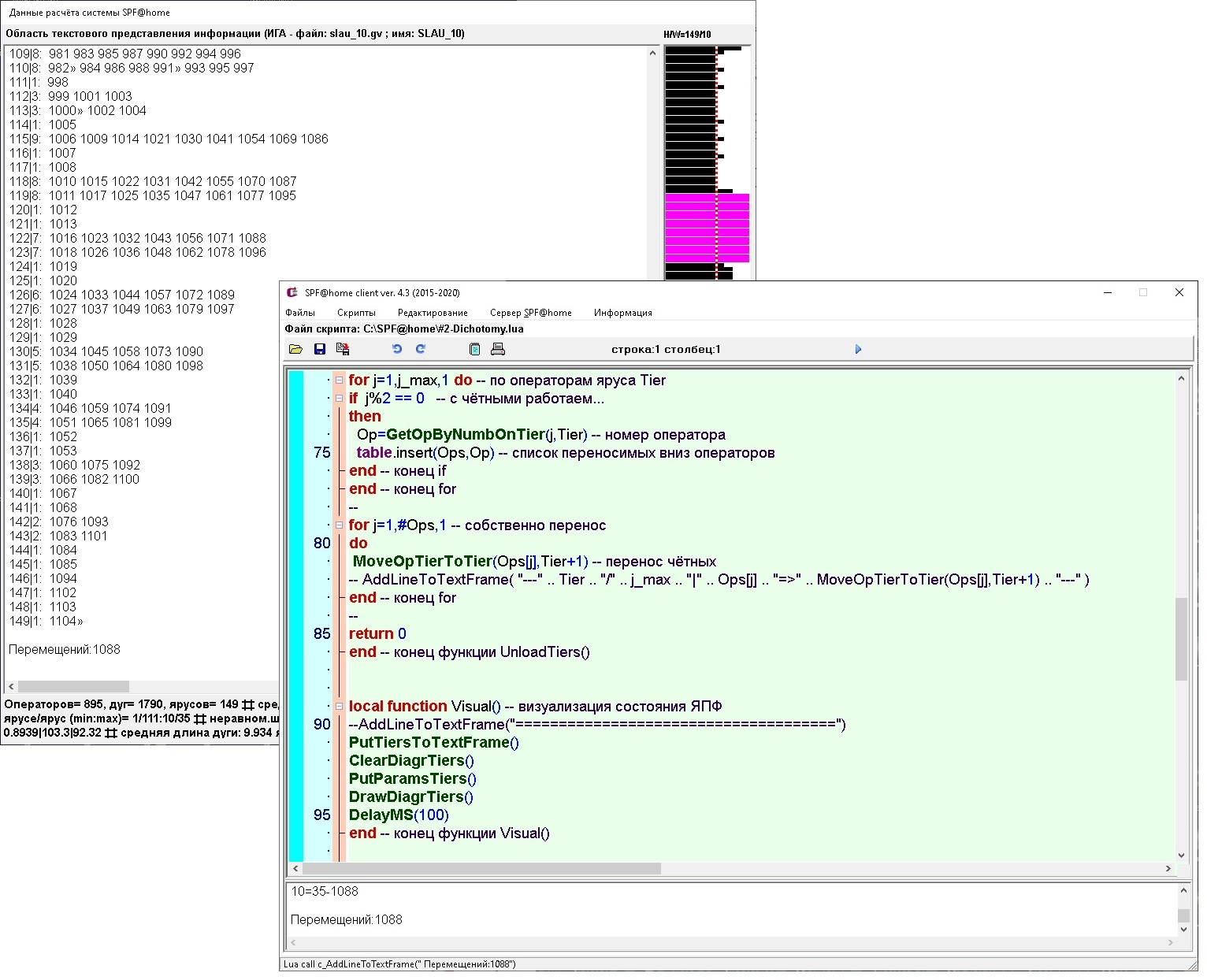
Модуль D-F (Data-Flow) является фактически универсальным вычислителем, выполняющим программу на ассемблероподобном языке на заданном числе параллельных вычислителей. При их числе большем 1 вычисления ведутся по принципу «Data-Flow» (реализуется статическая потоковая архитектура), операторы выполняются по условию готовности их к выполнению (ГКВ), что является следствием присвоенности значений все операндам данного оператора; при единичном вычислителе реализуется обычное последовательное выполнение. В случае превышения числа ГКВ-операторов числа свободных вычислители используется задаваемая система приоритетов их выполнения, условное выполнение реализуется предикатным выполнением, для реализации циклов используется система макросов, «разворачивающая» циклические структуры. Модуль D-F имеет встроенную систему проверку корректности ИГА, для контроля выполнения используется динамическая цветовая индикация выполненности операторов.
Программы для D-F составляются в императивном стиле, каждый оператор по уровню сложности сопоставим с уровнем ассемблера, порядок расположения операторов в программе несущественен. Нижеприведен пример записи программы вычисления вещественных корней полного квадратного уравнения (входной set-файл для модуля D-F, механизм предикатов в приведенном варианте не используется):
Такая программа может рассматриваться как результат компиляции с языков программирования высокого уровня, не содержащих явных указаний на параллелизацию вычислений. В модуле D-F программа отлаживается, результат выдается в файл ИГА-формата для обработки в модуле SPF@home. В модуле SPF@home для получения ЯПФ из gv-файла (стандартный формат текстовых файлов описаний графов), запоминания его во внутреннем представлении системы, создание ЯПФ и запоминание его в Lua-массиве для дальнейшей обработки может быть выполнен следующий код (наклоном выделены API-вызовы системы, двойной дефис означает начало комментария до конца строки):
CreateTiersByEdges("EdgesData.gv") -- создать ЯПФ по файлу EdgesData.gv
-- с подтянутостью операторов "вверх”
-- CreateTiersByEdges_Bottom("EdgesData.gv") -- создать ЯПФ по файлу EdgesData.gv
-- с подтянутостью операторов "вниз”
--
OpsOnTiers={} -- создаём пустой 1D-массив OpsOnTiers
for iTier=1,GetCountTiers() do -- по ярусам ЯПФ
OpsOnTiers[iTier]={} -- создаём iTier-тую строку 2D-массива OpsOnTiers
for nOp=1,GetCountOpsOnTier(iTier) do -- по порядковым номерам операторов на ярусе iTier
OpsOnTiers[iTier][nOp]=GetOpByNumbOnTier(nOp,iTier) -- взять номер оператора nOp
end end -- конец циклов for по iTier и for по nOpДля удобства данные метрик операторов и дуг графа выведены из gv-файлов и расположены в текстовых mvr и med-файлах, для моделирования выполнения программ на гетерогенном поле параллельных вычислителей служат cls и ops-файлы сопоставления возможностей выполнения определенных операторов на конкретных вычислителях. Преимуществом такого подхода является возможность задания нужных параметров целой группе объектов (списком типа «от-до», причем список может быть и вырожденным) одной строкой файла. Задавать параметры можно по практически неограниченному количеству тегов, определяемых разработчиком.
Модуль SPF@home также позволяет определять «время жизни данных» между ярусами ЯПФ, что необходимо для определения/оптимизации параметров устройств временного хранения данных (обычно регистров процессора). Собственно размер данных при этом берется из med-файлов.
Система нацелена в основном на анализ программ, созданных с использованием языков программирования высокого уровня без явного указания распараллеливания и в системах c концепцией ILP (Instruction-Level Parallelism, параллелизм на уровне команд), хотя возможности модуля SPF@home позволяют использовать в качестве неделимых блоков последовательности команд любого размера.
Т.о. процедура составления расписания параллельного выполнения программы заключается в составлении Lua-программы, реализующей процедуры реорганизации ЯПФ в соответствие с заданными требованиями. Тремя типовыми встречающимися подзадачами (в реальном случае обычно требуется выполнение нескольких из этих подзадач одновременно) являются:
I. «Балансировка» числа операторов по всем ярусам заданной ЯПФ без увеличения ее высоты (минимизируется требуемое для решения задачи число параллельных вычислителей).
II. Получение расписания выполнения программы на заданном числе параллельных вычислителей с возможным увеличением высоты ЯПФ (фактически временем выполнения программы).
III. Получение расписания выполнения программы на гетерогенном поле параллельных вычислителей.
Моделирования проводилось на часто используемых при расчетах алгоритмах (в основном из области линейной алгебры) относительно небольшой размерности по входным данным; автор искренне надеется на сохранение выявленных тенденций и для много больших размерностей (во многих случаях требуемый эффект с большей вероятностью достигается при возрастании размерности).
Кроме того, из общих соображений нет смысла оптимизировать всю (возможно, содержащую многие миллионы машинных команд) программу, рационально оптимизировать только участки, выполнение которых занимает максимум времени (выявление таких участков — самостоятельная задача и здесь не рассматривается).
Собственно последовательность получения рационального расписания выполнения параллельной задачи будут следующей:
1) Получение исходной (не имеющей ограничений по ширине ярусов) ЯПФ.
2) Модификация этой ЯПФ в нужном направлении путем целенаправленной перестановки операторов с яруса на ярус при сохранении исходных связей в информационном графе алгоритма.
Описанная процедура итеративна и является естественно-последовательной для решения поставленной задачи. Второй параграф последовательности выполнятся в зависимости от выбранных исследователя критериев оптимизации метода разработки расписания (получение ЯПФ минимальной ширины, заданное ограничение ширины ЯПФ, минимизация числа регистров временного хранения данных, комбинированная функция цели). При этом сначала выполняются «информационные» API-вызовы и на основе полученных данных реализуются «акционные» вызовы (дающие информацию о состоянии ЯПФ и осуществляющие реальную перестановку операторов соответственно, причем перед выполнением вторых всегда проверяется условие неизменности исходных информационных связей в графе после совершения действия).
При необходимости в любой момент можно «откатить» сделанные изменения (пользуясь данными файла протокола) и начать новый цикл реорганизации ЯПФ (графическая интерпретация ЯПФ в виде линейчатой диаграммы позволяет визуально отслеживать изменения ЯПФ). По желанию исследователя исходная ЯПФ может быть получена в «верхней» или «нижней» форме (все операторы расположены на ярусах с минимальными или максимальными номерами соответственно; при этом тенденции перемещения операторов по ярусам будут в основном «вниз» или «вверх»).
Методы достижения цели могут быть собственно разработанными эристиками (обычно ограниченной сложности для возможности использования в режиме реального времени) или стандартными — метод «ветвей и границ», генетические, «муравьиные» и др. (чаще используются при исследовательской работе). Возможности системы включают использование «оберток» многофункциональных системных Windows-вызовов WinExec, ShellExecute и CreateProcess, так что исследователь имеет возможность вызова и управления любыми внешними программами (например, использовать тот же METIS в качестве процесса-потомка), файловое обслуживание при этом осуществляется средствами Lua.
В качестве примера на рис. 6 приведены (в форме линейчатых диаграмм распределения ширин ярусов ЯПФ) результаты вычислительных экспериментов с общим символическим названием «Bulldozer», возникшим по аналогии с отвалом бульдозера, перемещающим грунт с «возвышенностей» во «впадины».
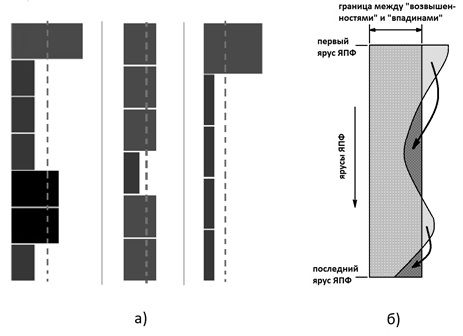На рис. показаны линейчатые диаграммы ширин ярусов реальных ЯПФ из копий экранов при работе системы SPF@home (средне-арифметическое значение ширин показано пунктиром, a) и символическая схема действия метода «Bulldozer» — б)
Многочисленные вычислительные эксперименты показывают, что во многих случаях удается значительно (до 1,5–2 раз) снизить ширину ЯПФ без увеличения высоты, но почти никогда до минимальной величины (средне-арифметическое значение ширин ярусов).
Т.о. истинной ценностью данного исследования являются именно эвристические методы (реализованные на языке Lua) создания расписаний выполнения параллельных программ при определённых ограничениях (напр., c учетом заданного поля параллельных вычислителей, максимума скорости выполнения, минимизации или ограничения размеров временного хранения данных и др.).
В систему SPF@home включена возможность расчета времени жизни локальных (для данного алгоритма) данных. Интересно, что даже при полностью последовательном выполнении алгоритма имеется возможность оптимизировать последовательность выполнения отдельных операторов с целью минимизации размера локальных данных. Выявленная возможность экономии устройств для хранения временных данных (в первую очередь дорогостоящих регистров общего назначения) прямо ведет к экономии вычислительных ресурсов (это может быть важно, например, для программируемых контроллеров и специализированных управляющих компьютеров). Полученные данные верны не только для однозадачного режима выполнения программ, но и применимы для многозадачности с перегрузкой контекстов процессов при многозадачности.
Целевыми потребителями разработанных методов генерации расписаний являются разработчики компиляторов, исследователи свойств алгоритмов (в первую очередь в направлении нахождения и использования потенциала скрытого параллелизма) и преподаватели соответствующих дисциплин.
Список литературы
1. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. — СПб.: БХВ-етербург, 2002. — 608 c.
2. Гери М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. : — Мир, Книга по Требованию, 2012. — 420 c.
3. AlgoWiki. Открытая энциклопедия свойств алгоритмов. URL: http://algowiki-project.org (дата обращения 31.07.2020).
4. Федотов И.Е. Параллельное программирование. Модели и приёмы. — М.: СОЛОН-Пресс, 2018. — 390 с.
5. Roberto Ierusalimschy. Programming in Lua. Third Edition. PUC-Rio, Brasil, Rio de Janeiro, 2013. — 348 p.
