Еще один алгоритм определения пересечения двух отрезков29.09.2015 17:19

Недавно была публикация "Простой алгоритм определения пересечения двух отрезков". Я решил попробовать решить задачу пересечения двух отрезков немного по-другому, более геометрически.
Нахождение точки пересечения двух отрезков.

Имеем 2 отрезка {P0,P1} и {P2,P3}, где P0,P1,P2,P3 точки на плоскости. Будем обозначать x y координаты точки P как P.x и P.y
Имеем координаты 4 точек в массиве P(0..3) структуры point(x float, y float):

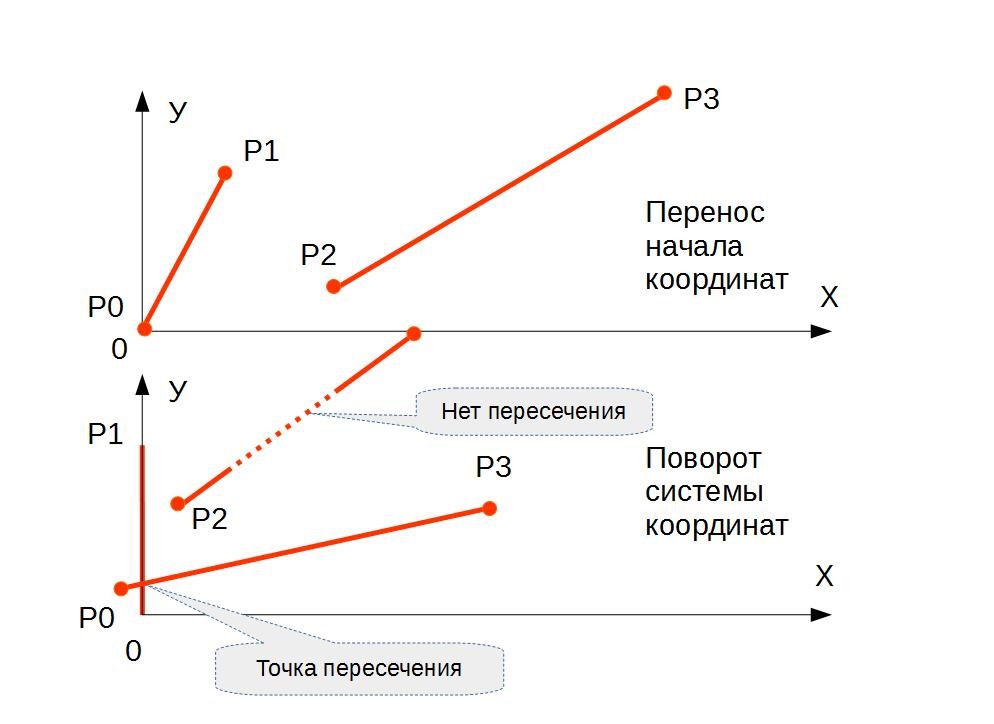
Шаг 1 — Перенос начала координат.

Запомним координаты точек P в дополнительном массиве P_copy. Перенесем начало системы координат в точку P0 и пересчитаем координаты точек:

P_copy = P
P(0).x = 0            ;  P(0).y = 0
for ii = 1 to 3 
   P(ii).x = P(ii).x - P_copy(1).x  ;  P(ii).y = P(ii).y - P_copy(1).y  
next 

Шаг 2 — Поворот начала координат
Повернем систему координат так, чтобы отрезок {P0,P1} принял вертикальное положение (лег на ось Y). Вычислим длину отрезка {P0,P1} как:
L1 = SQRT ( (P(1).x)^2 + (P(1).y)^2 )
Синус и косинус угла alfa поворота осей координат:

  если L1 > 0
     sin_alf = sin(alfa) = P(1).x / L1
     cos_alf = cos(alfa) = P(1).y / L1          
   если L1 = 0  // точку не поворачиваем
     sin_alf = 0
     cos_alf = 1

Cнова пересчитываем координаты точек P1,P2,P3:

   P(0).x = 0  ; P(0).y = 0  // Точка P0 не поворачивается, она в начале координат
   P(1).x = 0  ; P(1).y = L1
   P(2).x = P(2).x * cos_alf - P(2).y * sin_alf 
   P(2).y = P(2).y * cos_alf + P(2).x * sin_alf  
   P(3).x = P(3).x * cos_alf - P(3).y * sin_alf 
   P(3).y = P(3).y * cos_alf + P(3).x * sin_alf 

Шаг 3 — Поиск точки пересечения отрезков.

Запишем уравнение отрезка {P2,P3} и найдем точку его пересечения CR с осью Y:

P23X = P(2).x + ( P(3).x - P(2).x ) * beta
P23Y = P(2).y + ( P(3).y - P(2).y ) * beta
где 0 <= beta <= 1

В точке CR пересечения отрезка {P2,P3} с осью Y:
P(2).x + ( P(3).x - P(2).x ) * beta =0
Далее возможны 2 варианта в зависимости от значения P(3).x — P(2).x:

1 вариант:

  если  ( P(2).x - P(3).x ) <> 0 // отрезок {P2,P3} не вертикален
      beta  = P(2).x / ( P(2).x - P(3).x )
          если  beta >= 0 и beta <= 1  // отрезок {P2,P3} пересекает ось Y
            CR.x = 0 
        CR.y =  P(2).y + ( P(3).y - P(2).y ) *  beta
        //условие пересечения отрезков:         
               0 <= CR.y <= L1      

2 вариант:

Если P(2).x = P(3).x, то это означает, что отрезок {P2,P3} вертикален и параллелен отрезку {P0,P1}. Пересечение отрезков возможно только если второй отрезок {P2,P3} тоже лежит на оси Y, и один из его концов лежит в первом отрезке {P0,P1} (или касается) или отрезок {P2,P3} накрывает {P0,P1}. Будем считать что для результата нам достаточно одной точки. Это будет одна из точек P0..P3.

Условия:

   P(2).x = P(3).x = 0   // второй отрезок {P2,P3} вертикален b лежит на оси Y.
          и  // условие пересечения:
                P(2).y >= 0 и  P(2).y <= L1  // P2 внутри отрезка {P0,P1}
                         -> CR  = P_copy(2)   // результат выбираем вершину P2
                 или 
                P(3).y >= 0 и  P(3).y <= L1  // P3 внутри отрезка {P0,P1}
                    -> CR  = P_copy(3)  // результат выбираем вершину P3
                 или   
                     P(2).y < 0 и  P(3).y > L1  // отрезок {P0,P1} внутри отрезка {P2,P3}
                        или
                     P(3).y < 0 и  P(2).y > L1   
                  -> CR  = P_copy(0) // // результат выбираем вершину P0 (или P1)
            )    

Шаг 4

Если точка пересечения CR найдена по варианту 1 шага 3, то ее координаты пересчитываем для исходной системы координат. Используем переменные сохраненные на 1 и 2 шаге. Поворот на угол -alfa:

   CR.x = CR.x * cos(-alfa) + CR.y * sin(-alfa)  = CR.x * cos_alf + CR.y * sin_alf
   CR.y = CR.y * cos(-alfa) - CR.x * sin(-alfa)  = CR.y * cos_alf  - CR.x * sin_alf

Перенос обратно:

   CR.x = CR.x + P_copy(0).x 
   CR.y = CR.y + P_copy(0).y    

Если точка пересечения CR найдена по условию 2 шага 3 пересчет координат не нужен. Пример кода на golang под катом. Golang ом я только балуюсь, поэтому к коду прошу быть снисходительным. Код можно запустить на golang.org:

© Habrahabr.ru