Эксперименты с нейронными сетями на данных сейсморазведки
Сложность интерпретации данных сейсмической разведки связана с тем, что к каждой задаче необходимо искать индивидуальный подход, поскольку каждый набор таких данных уникален. Ручная обработка требует значительных трудозатрат, а результат часто содержит ошибки, связанные с человеческим фактором. Использование нейронных сетей для интерпретации может существенно сократить ручной труд, но уникальность данных накладывает ограничения на автоматизацию этой работы.
Данная статья описывает эксперимент по анализу применимости нейронных сетей для автоматизации выделения геологических слоев на 2D-изображениях на примере полностью размеченных данных из акватории Северного моря.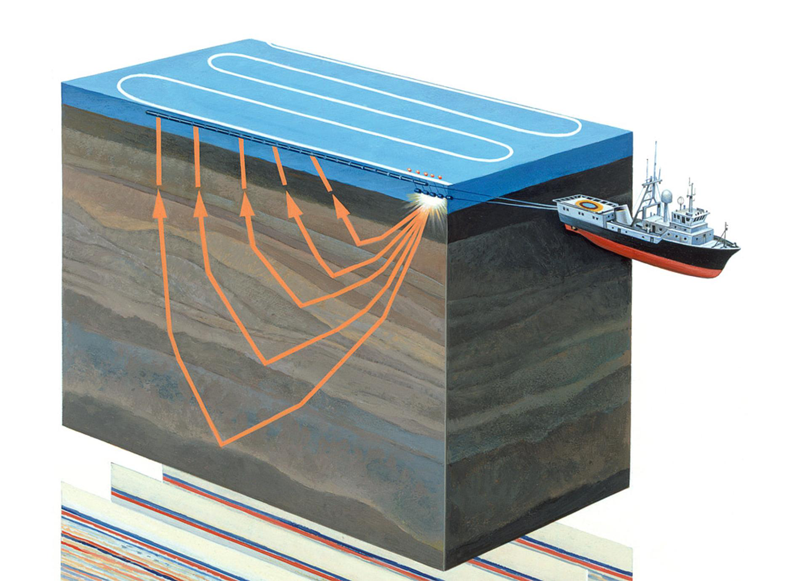
Рисунок 1. Проведение акваториальной сейсморазведки (источник)
Немного о предметной области
Сейсморазведка — геофизический метод изучения геологических объектов с помощью упругих колебаний — сейсмических волн. Этот метод основан на том, что скорость распространения сейсмических волн зависит от свойств геологической среды, в которой они распространяются (состава горных пород, их пористости, трещиноватости, влагонасыщенности и т.д.) Проходя через геологические слои с разными свойствами, сейсмические волны отражаются от различных объектов и возвращаются на приемник (см. рисунок 1). Их характер регистрируется и после обработки позволяет сформировать двумерное изображение — сейсмический разрез, или трехмерный массив данных — сейсмический куб.
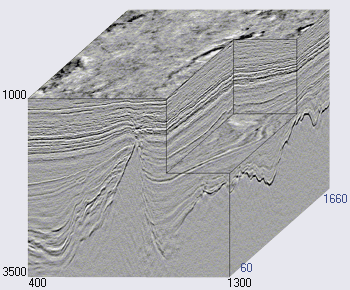
Рисунок 2. Пример сейсмического куба (источник)
Горизонтальные оси сейсмического куба располагаются вдоль земной поверхности, а вертикальная представляет глубину или время (см. рисунок 2). В некоторых случаях куб разбивается на вертикальные срезы вдоль оси расположения сейсмоприемников (так называемые инлайны, inlines) или поперек (кросслайны, crosslines, xlines). Каждая вертикаль куба (и среза) представляет собой отдельную сейсмотрассу.
Таким образом, инлайны и кросслайны состоят из одних и тех же сейсмотрасс, только в разном порядке. Соседние сейсмотрассы очень похожи друг на друга. Более резкое изменение происходит в местах разломов, но сходство все равно будет. Значит, и соседние срезы очень похожи друг на друга.
Все эти знания нам пригодятся при планировании экспериментов.
Задача интерпретации и роль нейронных сетей в ее решении
Полученные данные вручную обрабатываются специалистами-интерпретаторами, которые выделяют непосредственно на кубе или на каждом его срезе отдельные геологические слои пород и их границы (горизонты, horizons), залежи соли, разломы и прочие особенности геологического строения исследуемой зоны. Интерпретатор, работая с кубом или срезом, начинает свою работу с кропотливого ручного выделения геологических слоев и горизонтов. Каждый горизонт необходимо вручную пропикировать (от английского «picking» — cбор) указанием курсора и щелчком мыши.
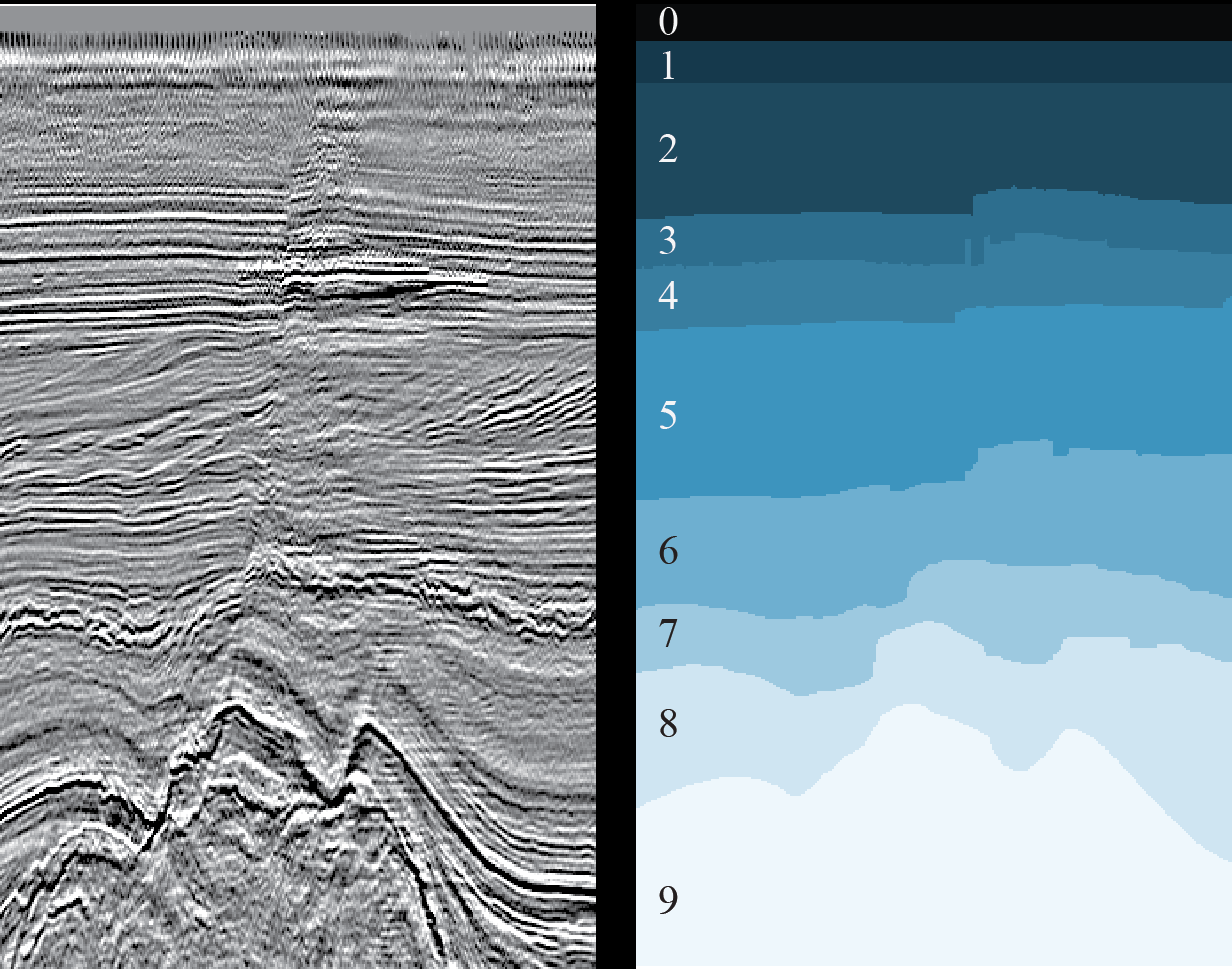
Рисунок 3. Пример 2D-среза (слева) и результата разметки соответствующих ему геологических слоев (справа) (источник)
Основная проблема связана с нарастающим с каждым годом объемом сейсмических данных, получаемых во все более сложных геологических условиях (например, подводные участки с большими глубинами моря), и неоднозначностью интерпретации этих данных. Кроме того, в условиях сжатых сроков и/или больших объемов интерпретатор неизбежно допускает ошибки, например, пропускает различные особенности геологического разреза.
Эту проблему можно частично решить с помощью нейронных сетей, значительно сократив ручной труд, ускорив тем самым процесс интерпретации и уменьшив количество ошибок. Для работы нейросети необходимо некоторое количество уже готовых, размеченных срезов (участков куба), а в результате будет получена полная разметка всех срезов (или всего куба), которая в идеале потребует лишь незначительной доработки человеком по корректировке отдельных участков горизонтов или переразметке небольших зон, которые сеть не смогла распознать корректно.
Решений задач интерпретации с помощью нейросетей много, вот лишь несколько примеров: раз, два, три. Сложность заключается в том, что каждый набор данных уникален — из-за особенностей геологических пород исследуемого региона, из-за различных технических средств и методик проведения сейсморазведки, из-за разнообразных используемых методов превращения сырых данных в готовые для интерпретации. Даже из-за внешних шумов (например, собачьего лая и других громких звуков), которые не всегда удается полностью убрать. Поэтому каждую задачу приходится решать индивидуально.
Но, несмотря на это, многочисленные работы позволяют нащупать отдельные общие подходы к решению различных задач интерпретации.
Мы в MaritimeAI (проект, развившийся из Machine Learning for Social Goods ODS-сообщества, статья о нас) для каждой зоны поля наших интересов (исследование моря) изучаем уже опубликованные работы и проводим собственные эксперименты, позволяющие нам уточнить границы и особенности применения тех или иных решений, а иногда и найти собственные подходы.
Результаты одного эксперимента мы и описываем в данной статье.
Бизнес-цели исследования
Специалисту по Data Science достаточно взглянуть на рисунок 3, чтобы облегченно вздохнуть — обычная задача семантической сегментации изображений, для которой придумано множество архитектур нейронных сетей и методов обучения. Надо лишь выбрать подходящие и обучить сеть.
Но не все так просто.
Для получения хорошего результата с помощью нейронной сети нужно как можно больше уже размеченных данных, на которых она будет учиться. Но наша задача как раз и состоит в том, чтобы сократить количество ручной работы. А использовать размеченные данные из других регионов редко когда удается из-за их сильных различий в геологическом строении.
Переведем вышесказанное на язык бизнеса.
Чтобы использование нейросетей было экономически оправданным, нужно максимально сократить объем первичной ручной интерпретации и доработок полученных результатов. Но уменьшение данных для обучения сети отрицательно скажется на качестве ее результата. Так сможет ли нейросеть ускорить и облегчить работу интерпретаторов и повысить качество размеченных изображений? Или только усложнит привычный процесс?
Целью данного исследования является попытка определения минимально достаточного для нейронной сети объема размеченных данных сейсмического куба и оценки получаемых результатов. Мы попробовали найти ответы на следующие вопросы, которые должны помочь «владельцам» результатов проведенной сейсморазведки в принятии решения о ручной или частично автоматизированной интерпретации:
- Какой объем данных необходимо разметить специалистам для обучения нейронной сети? И какие данные для этого следует выбирать?
- Что при таком объеме получится на выходе? Нужна ли будет ручная доработка предсказаний нейронной сети? Если да — насколько сложная и объемная?
Общее описание эксперимента и использованных данных
Для эксперимента мы выбрали одну из задач интерпретации, а именно задачу выделения геологических слоев на 2D-срезах сейсмического куба (см. рисунок 3). Эту задачу уже пробовали решать (см. здесь) и, по словам авторов, получили неплохой результат на 1% случайно выбранных срезов. С учетом объема куба, это 16 изображений. Однако в статье не приведены метрики для сравнения и отсутствует описание методики обучения (функция потерь, оптимизатор, схема изменения скорости обучения и т.п.), что делает эксперимент невоспроизводимым.
К тому же, приведенные там результаты, на наш взгляд, недостаточны для получения полных ответов на поставленные вопросы. Оптимально ли это значение в 1%? А, может, для другой выборки срезов оно будет иным? Можно ли выбрать меньше данных? Стоит ли взять больше? Как изменится результат? И т.п.
Для эксперимента мы взяли тот же набор полностью размеченных данных из голландского сектора акватории Северного моря. Исходные сейсмические данные представлены на сайте Open Seismic Repository: Project Netherlands Offshore F3 Block. Их краткое описание можно найти в статье Silva et al. «Netherlands Dataset: A New Public Dataset for Machine Learning in Seismic Interpretation».
Поскольку в нашем случае речь идет о 2D-срезах, мы использовали не исходный 3D-куб, а уже сделанную «нарезку», доступную здесь: Netherlands F3 Interpretation Dataset.
В процессе эксперимента мы решили следующие задачи:
- Просмотрели исходные данные и отобрали срезы, которые по качеству ближе всего к ручной разметке.
- Зафиксировали архитектуру нейронной сети, методику и параметры обучения и принцип выбора срезов для обучения и валидации.
- Обучили 20 одинаковых нейронных сетей на разном объеме данных одного типа срезов для сравнения результатов.
- Обучили еще 20 нейронных сетей на разном объеме данных разного типа срезов для сравнения результатов.
- Оценили объем необходимой ручной доработки результатов прогноза.
Результаты эксперимента в виде оценочных метрик и предсказанных сетями масок срезов представлены далее.
Задача 1. Отбор данных
Итак, в качестве исходных данных мы использовали готовые инлайны и кросслайны сейсмического куба из голландского сектора акватории Северного моря. Детальный анализ показал, что там не все гладко — есть немало изображений и масок с артефактами и даже сильно искаженных (см. рисунки 4 и 5).

Рисунок 4. Пример маски с артефактами
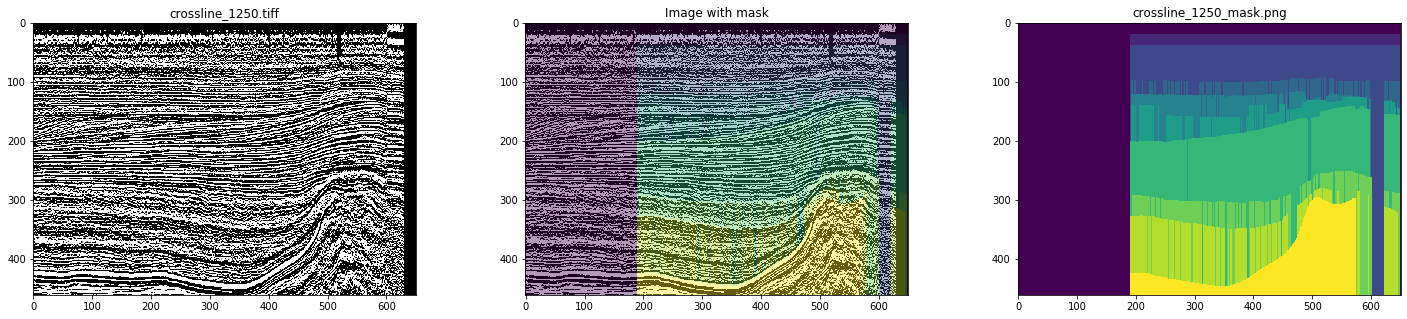
Рисунок 5. Пример искаженной маски
При ручной разметке ничего подобного наблюдаться не будет. Поэтому, имитируя работу интерпретатора, для обучения сети мы выбрали только чистые маски, просмотрев все срезы. В результате было отобрано 700 кросслайнов и 400 инлайнов.
Задача 2. Фиксирование параметров эксперимента
Данный раздел представляет интерес, в первую очередь, для специалистов по Data Science, поэтому будет использоваться соответствующая терминология.
Поскольку инлайны и кросслайны состоят из одних и тех же сейсмотрасс, можно выдвинуть две взаимоисключающие гипотезы:
- Обучение можно проводить только на одном типе срезов (например, на инлайнах), используя изображения другого типа как отложенную выборку. Это даст более адекватную оценку результата, т.к. оставшиеся срезы того же типа, что использовался при обучении, все равно будут похожи на тренировочные.
- Для обучения лучше использовать смесь срезов разных типов, поскольку это уже готовая аугментация.
Проверим.
Кроме того, схожесть соседних срезов одного типа и желание получить воспроизводимый результат привели нас к стратегии выбора срезов для обучения и валидации не по произвольному принципу, а равномерно по всему кубу, т.е. чтобы срезы были максимально удалены друг от друга, и, следовательно, охватывали максимальное разнообразие данных.
Для валидации использовались по 2 среза, так же равномерно распределенные между соседними изображениями тренировочной выборки. Например, для случая тренировочной выборки из 3 инлайнов валидационная выборка состояла из 4 инлайнов, для 3 инлайнов и 3 кросслайнов — из 8 срезов соответственно.
В итоге мы провели 2 серии обучений:
- Обучение на выборках инлайнов от 3 до 20 равномерно распределенных по кубу срезов с проверкой результата предсказаний сети на оставшихся инлайнах и на всех кросслайнах. Дополнительно было проведено обучение на 80 и 160 срезах.
- Обучение на объединенных выборках из инлайнов и кросслайнов по 3–10 равномерно распределенных по кубу срезов каждого типа с проверкой результата предсказаний сети на оставшихся изображениях. Дополнительно было проведено обучение на 40+40 и 80+80 срезах.
При таком подходе нужно учитывать, что размеры тренировочной и валидационной выборок существенно меняются, что затрудняет сравнение, но объем оставшихся изображений уменьшается не так сильно, что позволяет использовать их для вполне адекватной оценки изменений результата.
Для уменьшения переобучения для тренировочной выборки использовалась аугментация с произвольными кропами размером 448×64 и зеркальным отражением вдоль вертикальной оси с вероятностью 0.5.
Поскольку нас интересует зависимость качества результата только лишь от количества срезов в обучающей выборке, то предобработкой изображений можно пренебречь. Мы использовали один слой PNG-изображений без каких-либо изменений.
По этой же причине в рамках данного эксперимента нет необходимости искать наилучшую архитектуру сети — главное, чтобы она была одинаковой на каждом шаге. Мы выбрали простой, но хорошо себя зарекомендовавший на таких задачах UNet:

Рисунок 6. Архитектура сети
Функция потерь состояла из комбинации коэффициента Жаккарда и бинарной кроссэнтропии:
def jaccard_loss(y_true, y_pred):
smoothing = 1.
intersection = tf.reduce_sum(y_true * y_pred, axis = (1, 2))
union = tf.reduce_sum(y_true + y_pred, axis = (1, 2))
jaccard = (intersection + smoothing) / (union - intersection + smoothing)
return 1. - tf.reduce_mean(jaccard)
def loss(y_true, y_pred):
return 0.75 * jaccard_loss(y_true, y_pred) + 0.25 * keras.losses.binary_crossentropy(y_true, y_pred)
Прочие параметры обучения:
keras.optimizers.SGD(lr = 0.01, momentum = 0.9, nesterov = True)
keras.callbacks.EarlyStopping(monitor = 'val_loss', patience = 10),
keras.callbacks.ReduceLROnPlateau(monitor = 'val_loss', patience = 5)
Для уменьшения влияния произвольности выбора начальных весов на результаты, сеть была обучена на 3-х инлайнах в течение 1 эпохи. Все остальные обучения стартовали с этих полученных весов.
Обучение каждой сети проводилось на видеокарте GeForce GTX 1060 6Gb в течение 30–60 эпох. Обучение каждой эпохи занимало 10–30 секунд в зависимости от размера выборки.
Задача 3. Обучение на одном типе срезов (на инлайнах)
Первая серия состояла из 18-ти независимых обучений сети на 3–20 инлайнах. И, хотя нас интересует только оценка коэффициента Жаккарда на срезах, не использованных в обучении и валидации, интересно рассмотреть все графики.
Напомним, что результатами интерпретации каждого среза являются 10 классов (геологических слоев), которые на рисунках далее отмечены номерами от 0 до 9.

Рисунок 7. Коэффициент Жаккарда для обучающей выборки

Рисунок 8. Коэффициент Жаккарда для валидационной выборки
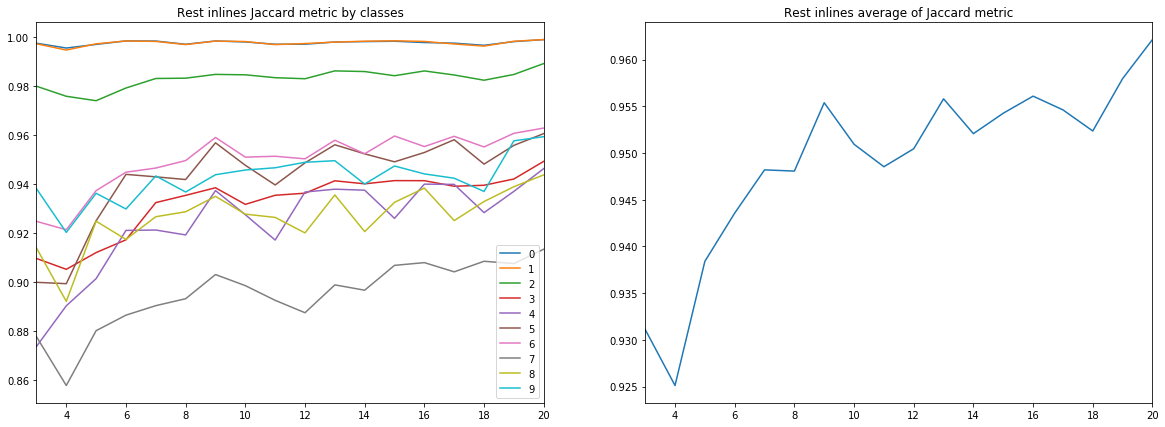
Рисунок 9. Коэффициент Жаккарда для остальных инлайнов
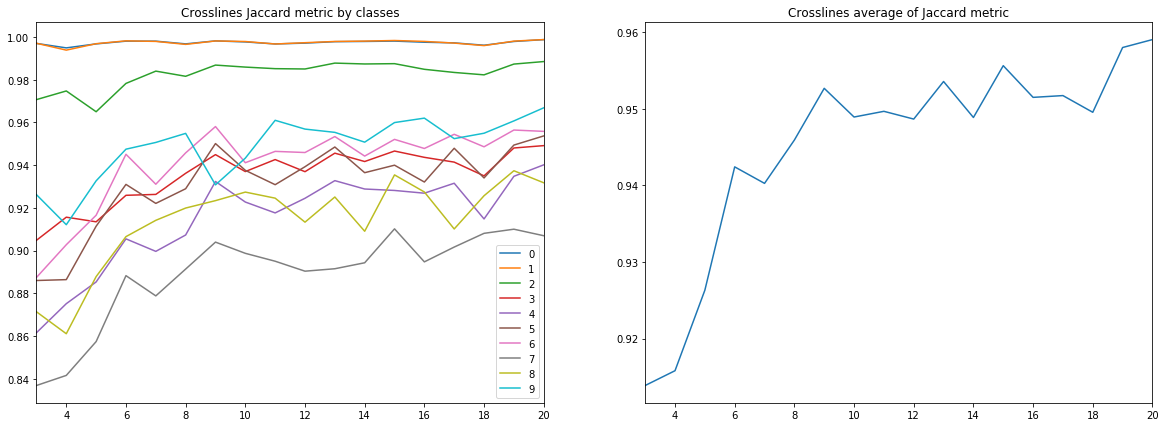
Рисунок 10. Коэффициент Жаккарда для кросслайнов
Из приведенных диаграмм можно сделать ряд выводов.
Во-первых, качество прогноза, измеренное по коэффициенту Жаккарда, уже на 9-ти инлайнах достигает весьма высокого значения, после чего продолжает расти, но уже не так интенсивно. Т.е. гипотеза о достаточности малого количества размеченных изображений для обучения нейросети подтверждается.
Во-вторых, весьма высокий результат получен и для кросслайнов, несмотря на то, что для обучения и валидации использовались только инлайны — подтверждается и гипотеза о достаточности только одного типа срезов. Однако, для окончательного вывода нужно сравнить результаты с обучением на смеси инлайнов и кросслайнов.
В-третьих, метрики для разных слоев, т.е. качество их распознавания, сильно отличаются. Это наталкивает на мысль о выборе другой стратегии обучения, например, использовании весов или дополнительных сетей для слабых классов, или полноценной схеме «one vs all».
И, наконец, следует отметить, что коэффициент Жаккарда не может дать полную характеристику качества результата. Для оценки предсказаний сети в данном случае лучше посмотреть на сами полученные маски, чтобы оценить их пригодность для доработки интерпретатором.
На следующих рисунках, показана разметка сетью, обученной на 10-ти инлайнах. Второй столбец, отмеченный как «GT mask» (Ground Truth mask), представляет собой целевую интерпретацию, третий — предсказание нейронной сети.


Рисунок 11. Примеры прогнозов сети для инлайнов
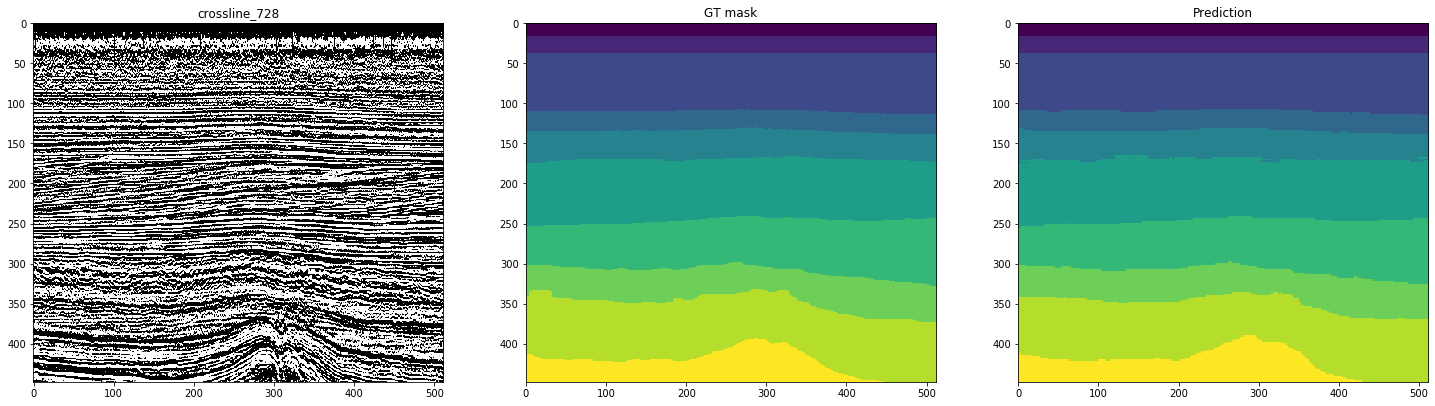

Рисунок 12. Примеры прогнозов сети для кросслайнов
Из рисунков видно, что наряду с достаточно чистыми масками, сеть затрудняется в распознавании сложных случаев даже на самих инлайнах. Таким образом, несмотря на достаточно высокую метрику для 10-ти срезов, часть полученных результатов будет требовать значительной доработки.
Рассмотренные нами размеры выборок колеблются около 1% от всего объема данных — и это уже позволяет неплохо разметить часть оставшихся срезов. Стоит ли увеличить количество первоначально размеченных срезов? Даст ли это сопоставимый прирост в качестве?
Рассмотрим динамику изменения результатов прогноза сетями, обученными на 5, 10, 15, 20, 80 (5% от полного объема куба) и 160 (10%) инлайнах на примере одних и тех же срезов.
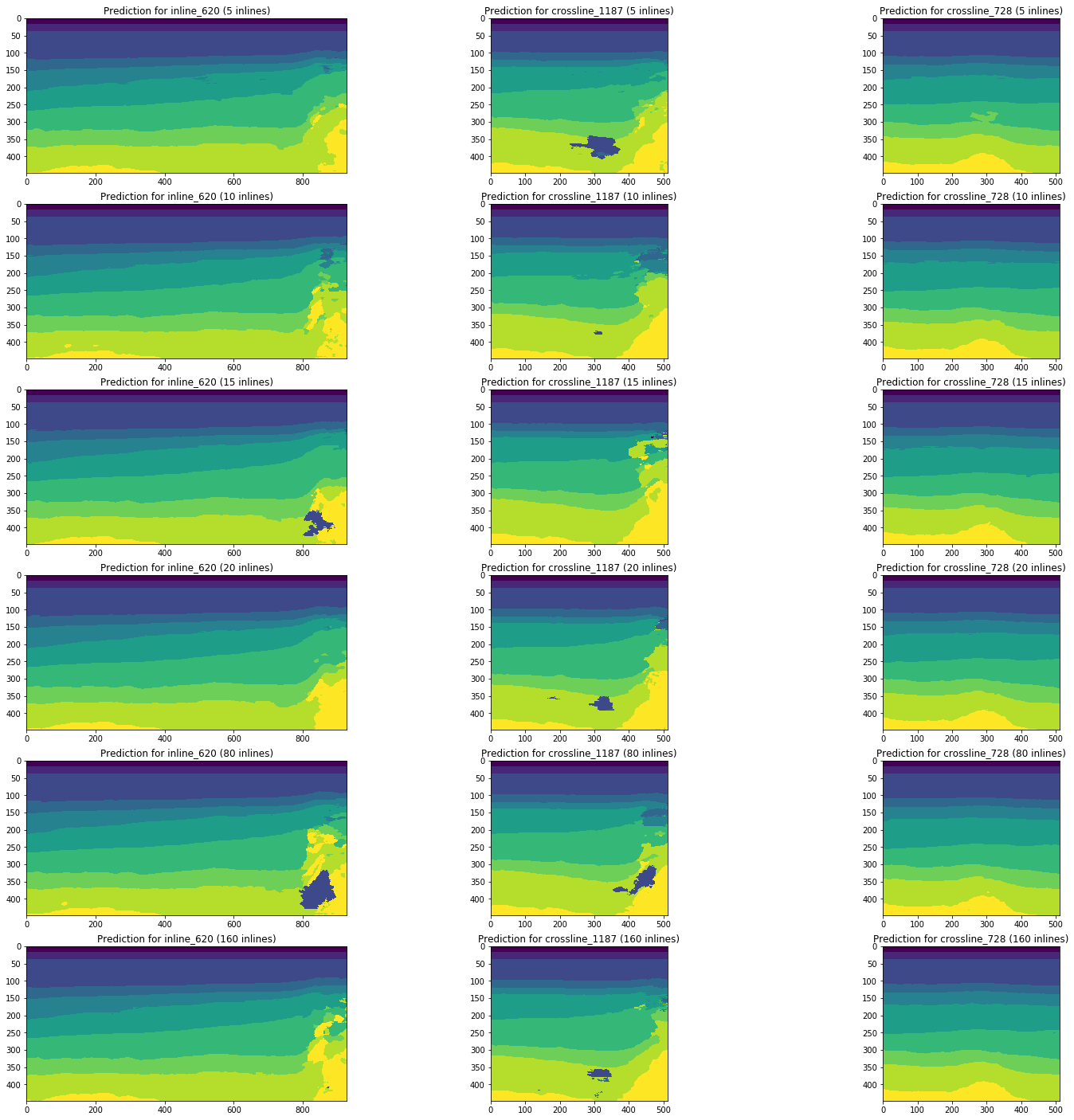
Рисунок 13. Примеры прогнозов сетей, обученных на разном объеме обучающей выборки
Из рисунка 13 видно, что увеличение объема тренировочной выборки в 5 и даже 10 раз не приводит к значимому улучшению. Срезы, которые хорошо распознавались уже на 10-ти тренировочных изображениях, не ухудшаются.
Таким образом, даже простая сеть без настройки и предобработки изображений способна интерпретировать часть срезов с достаточно высоким качеством при малом количестве размеченных вручную изображений. Вопрос доли таких интерпретаций и сложности доработки плохо распознанных срезов мы рассмотрим далее.
Аккуратный подбор архитектуры, параметров сети и обучения, предобработка изображений способны улучшить эти результаты на том же объеме размеченных данных. Но это уже выходит за рамки текущего эксперимента.
Задача 4. Обучение на разных типах срезов (инлайны и кросслайны)
Теперь сравним результаты этой серии с прогнозами, полученными при обучении на смеси инлайнов и кросслайнов.
На представленных ниже диаграммах приведены оценки коэффициента Жаккарда для разных выборок, в том числе, в сравнении с результатами предыдущей серии. Для сравнения (см. правые диаграммы на рисунках) были взяты только выборки одинакового объема, т.е. 10 инлайнов vs 5 инлайнов + 5 кросслайнов и т.п.

Рисунок 14. Коэффициент Жаккарда для обучающей выборки

Рисунок 15. Коэффициент Жаккарда для валидационной выборки

Рисунок 16. Коэффициент Жаккарда для остальных инлайнов

Рисунок 17. Коэффициент Жаккарда для остальных кросслайнов
Диаграммы наглядно иллюстрируют, что добавление срезов другого типа не улучшает результаты. Даже в разрезе классов (см. рисунок 18) влияния кросслайнов не наблюдается ни для одного из рассмотренных размеров выборок.

Рисунок 18. Коэффициент Жаккарда для разных классов (по оси Х) и разных размеров и состава тренировочной выборки
Для полноты картины сравним результаты прогноза сети на тех же срезах:
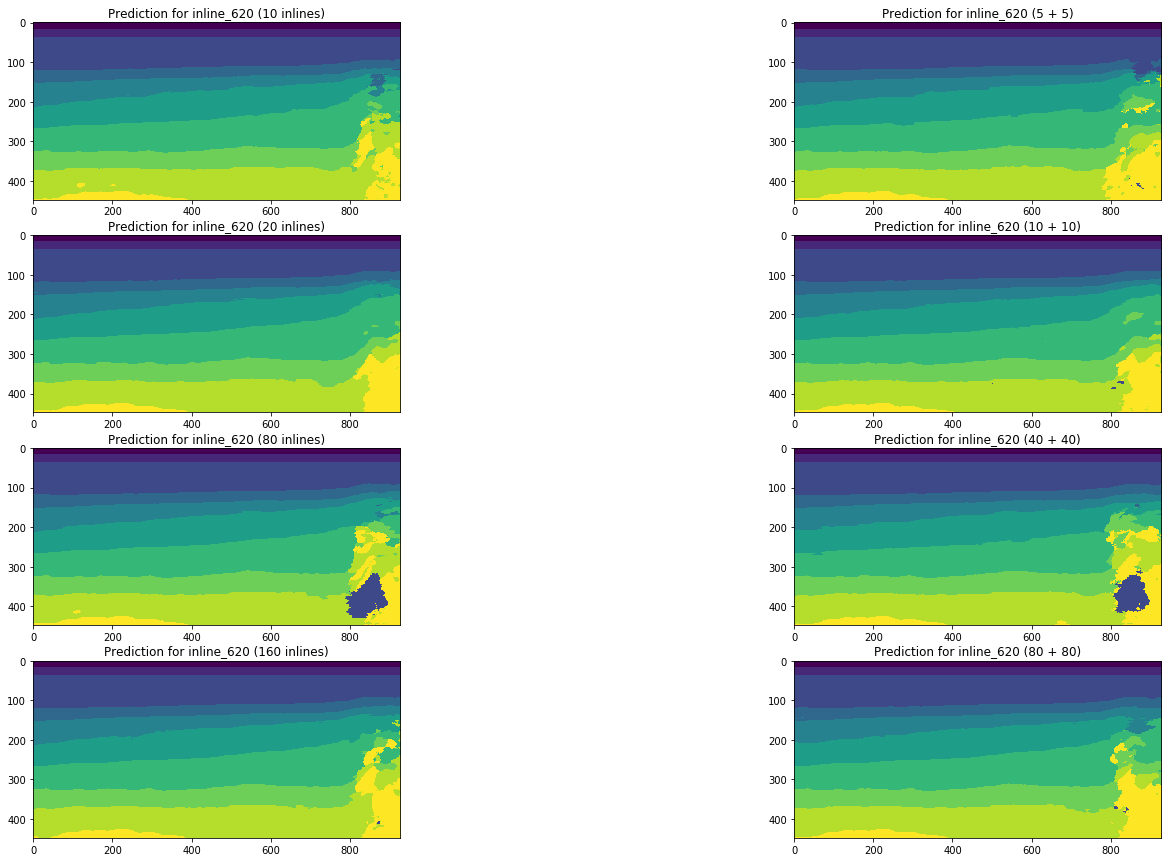
Рисунок 19. Сравнение прогнозов сети для инлайна
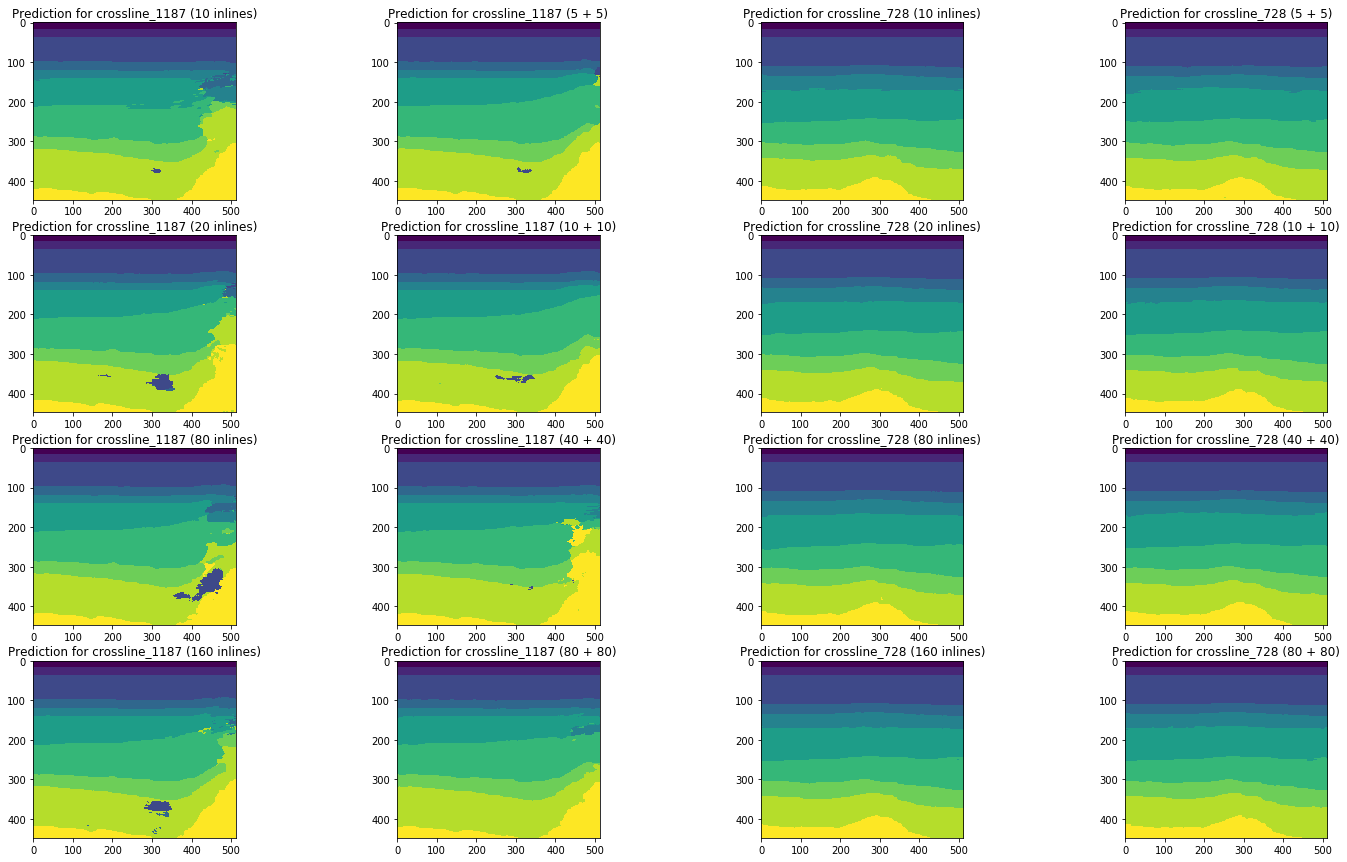
Рисунок 20. Сравнение прогнозов сети для кросслайнов
Визуальное сравнение подтверждает предположение о том, что добавление к обучению срезов другого типа кардинально ситуацию не меняет. Некоторые улучшения можно наблюдать только для левого кросслайна, но носят ли они глобальный характер? На этот вопрос мы попробуем ответить далее.
Задача 5. Оценка объема ручной доработки
Для окончательного вывода о результатах нужно оценить объем ручной доработки полученных прогнозов сети. Для этого мы определили количество компонент связности (т.е. сплошных пятен одного цвета) на каждом полученном прогнозе. Если это значение равно 10, то слои выделены правильно и речь идет максимум о незначительной коррекции горизонтов. Если их ненамного больше, то потребуется лишь «чистка» небольших зон изображения. Если их существенно больше, то все плохо и может даже понадобится полная переразметка.
Для проверки мы выбрали 110 инлайнов и 360 кросслайнов, которые не использовались в обучении ни одной из рассмотренных сетей.
Таблица 1. Статистики, усредненные по обоим типам срезов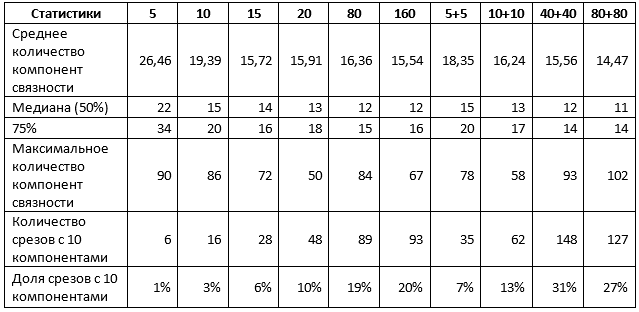
Таблица 1 подтверждает часть сделанных ранее результатов. В частности, при использовании для обучения 1% срезов нет разницы, использовать один тип срезов или оба, а получаемый результат можно охарактеризовать следующим образом:
- около 10% прогнозов близки к идеальным, т.е. потребуют не более чем корректировки отдельных участков горизонтов;
- 50% прогнозов содержат не более 15 пятен, т.е. не более 5 лишних;
- 75% прогнозов содержат не более 20 пятен, т.е. не более 10 лишних;
- оставшиеся 25% прогнозов требуют более существенной доработки, включая, возможно, полную переразметку единичных срезов.
Увеличение объема выборки до 5% меняет ситуацию. В частности, сети, обученные на смеси срезов, показывают значимо более высокие показатели, хотя максимальное значение компонент также возрастает, что свидетельствует о появлении отдельных интерпретаций очень плохого качества. Тем не менее, при увеличении выборки в 5 раз и использовании смеси срезов:
- около 30% прогнозов близки к идеальным, т.е. потребуют не более чем корректировки отдельных участков горизонтов;
- 50% прогнозов содержат не более 12 пятен, т.е. не более 2 лишних;
- 75% прогнозов содержат не более 14 пятен, т.е. не более 4 лишних;
- оставшиеся 25% прогнозов требуют более существенной доработки, включая, возможно, полную переразметку единичных срезов.
Дальнейшее увеличение объема выборки не приводит к улучшению результатов.
В целом для рассмотренного нами куба данных можно сделать выводы о достаточности 1–5% от общего объема данных для получения от нейронной сети неплохого результата.
По таким данным, в совокупности с приведенными ранее метриками и иллюстрациями, уже можно делать выводы о целесообразности использования нейронных сетей для помощи интерпретаторам и о тех результатах, с которыми специалисты будут иметь дело.
Выводы
Итак, теперь мы можем ответить на поставленные в начале статьи вопросы, оперируя результатами, полученными на примере сейсмического куба акватории Северного моря:
Какой объем данных необходимо разметить специалистам для обучения нейронной сети? И какие данные следует выбирать?
Для получения неплохого прогноза сети действительно достаточно предварительно разметить 1–5% от общего количества срезов. Дальнейшее увеличение объема не приводит к улучшению результата, сопоставимому с ростом количества предварительно размеченных данных. Для получения более качественной разметки на столь малом объеме с помощью нейронной сети необходимо пробовать другие подходы, например, тонкую настройку архитектуры и стратегии обучения, предобработку изображений и т.п.
Для предварительной разметки стоит выбирать срезы обоих типов — инлайны и кросслайны.
Что при таком объеме получится на выходе? Нужна ли будет ручная доработка предсказаний нейронной сети? Если да — насколько сложная и объемная?
В результате значительная часть размеченных такой нейронной сетью изображений потребует не самой значительной доработки, состоящей из коррекции отдельных плохо распознанных зон. Среди них будут встречаться и такие интерпретации, которые никаких правок не потребуют. И лишь для единичных изображений, возможно, понадобится новая ручная разметка.
Разумеется, при оптимизации алгоритма обучения и параметров сети можно улучшить ее прогнозные способности. В наш эксперимент решение таких задач не входило.
Кроме того, результаты одного исследования на одном сейсмическом кубе не стоит бездумно обобщать — именно вследствие уникальности каждого набора данных. Но эти результаты — подтверждение эксперимента, проведенного другими авторами, и основа для сравнения с нашими последующими исследованиями, о которых мы тоже вскоре напишем.
Благодарности
И в конце мне бы хотелось поблагодарить моих коллег из MaritimeAI (особенно Андрея Кохана) и ODS за ценные комментарии и помощь!
Список использованных источников:
- Bas Peters, Eldad Haber, Justin Granek. Neural-networks for geophysicists and their application to seismic data interpretation
- Hao Wu, Bo Zhang. A deep convolutional encoder-decoder neural network in assisting seismic horizon tracking
- Thilo Wrona, Indranil Pan, Robert L. Gawthorpe, and Haakon Fossen. Seismic facies analysis using machine learning
- Reinaldo Mozart Silva, Lais Baroni, Rodrigo S. Ferreira, Daniel Civitarese, Daniela Szwarcman, Emilio Vital Brazil. Netherlands Dataset: A New Public Dataset for Machine Learning in Seismic Interpretation
