Эксперимент: Что гипотеза случайного блуждания говорит о прогнозировании финансовых рынков05.04.2016 14:03

В нашем блоге на Хабре мы много пишем об алгоритмах и инструментах прогнозирования движения на финансовы рынках. При этом многие наблюдатели считают, что подобные занятия сродни игре в казино — на бирже все случайно, а значит ничего нельзя спрогнозировать. Количественный аналитик хедж-фонда NMRQL Стюарт Рид опубликовал на сайте Turing Finance результаты исследования, в ходе которого использовал гипотезу случайного блуждания, пытаясь подтвердить или опровергнуть тезис о случайности финансовых рынков. Мы представляем вашему вниманию основные мысли этого материала.

Как пишет Рид, хакеры и трейдеры, по сути, занимаются одним и тем же — они находят неэффективность системы и эксплуатируют ее. Разница лишь в том, что одни, преследуя самые разные цели, взламывают компьютеры, сети или даже людей, а вторые — финансовые рынки и их цель заключается в извлечении прибыли.

В этом контексте очень интересна тема генераторов случайных чисел — их используют для шифрования данных и коммуникаций, однако если в генераторе обнаружится уязвимость, то он перестает быть защищенным, а хакеры могут использовать ошибку, чтобы дешифровать информацию. Существуют различные наборы тестов, которые такие генераторы должны пройти, чтобы можно было оценить их криптостойкость. Одним из таких наборов является группа тестов NIST. В этом материале мы рассмотрим применение этих тестов к финансовым стратегиям, чтобы понять, можно ли «взломать» рынок.

Гипотеза случайного блуждания

В реальном мире многие системы демонстрируют свойства случайности. Например — распространение эпидемий вроде Эболы, поведение космической радиации, движение частиц в воде, удача во время игры в рулетку, и, согласно гипотезе случайного блуждания, даже движения финансовых рынков.

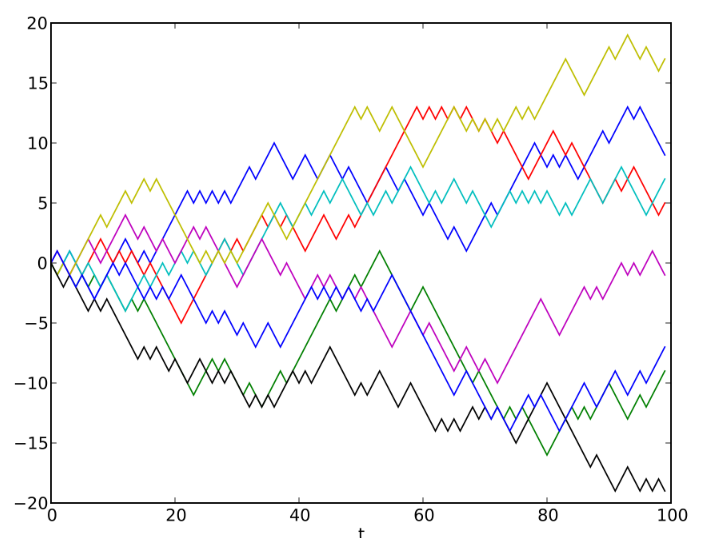
Рассмотрим интересный тест, проведенный профессором экономики Принстонского университета Бертоном Малкиелем (Burton G. Malkiel). В его ходе студентам «выдавалас » гипотетическая акция, которая изначально стоила $50. Цена закрытия торгов для этой акции каждый день определялась с помощью подбрасывания монетки. Если выпадал орел, то цена была на полпункта выше, а в случае решки — полпунтка ниже. Таким образом, каждый раз шанс на рост или падение стоимости по сравнению с предыдущим «торговым днем» составлял 50%. Таким образом определялись ценовые циклы и тренды.

Впоследствии Малкиель визуализировал результаты с помощью графиков и показал их «чартистам», то есть специалистам, которые прогнозировали будущие движения цен на основе паттернов их прошлых колебаний. Чартисты советовали ему немедленно покупать акции. Но поскольку эта акция не существовала, а ее цена определялась подбрасыванием монетки, то никаких реальных паттернов не существовало, а значит не могло быть и тренда. Результат эксперимента позволил Малкиелю утверждать, что фондовый рынок столь же случаен, как подбрасывание монетки.

Это похоже на «финансовый тест Тьюринга», в ходе которого людям, знакомым с финансовым рынком, предлагается взглянуть на график временных серий и определить, на каком их них реальные рыночные данные, какой представляет собой симуляцию с помощью случайных процессов:

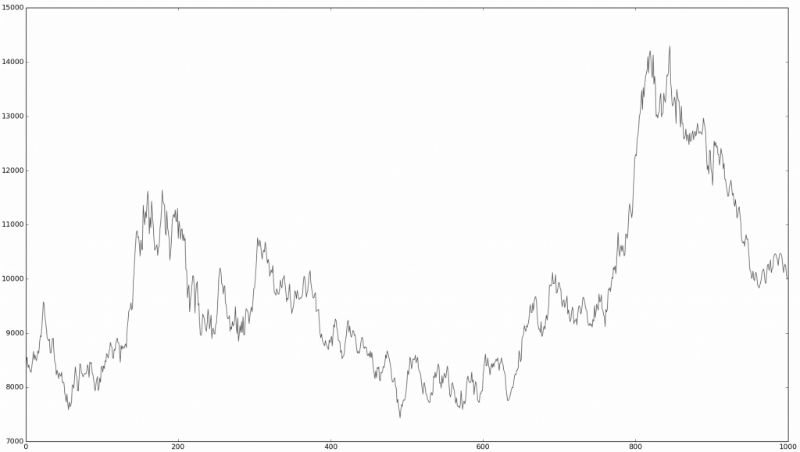
Это реальный рынок?

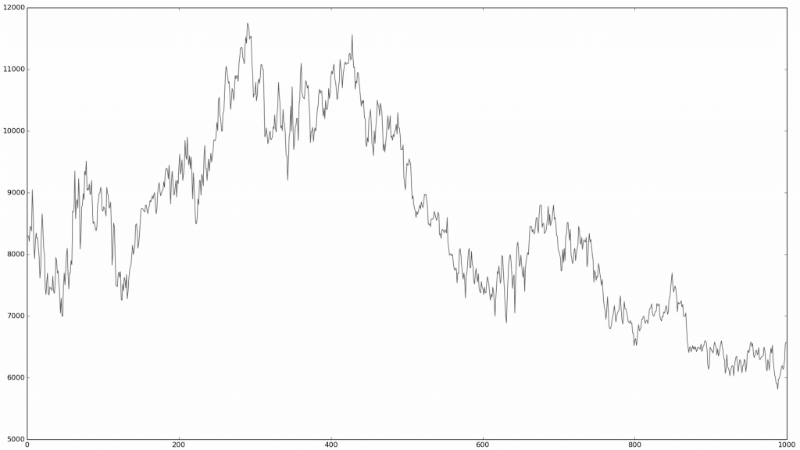
А это случайный?

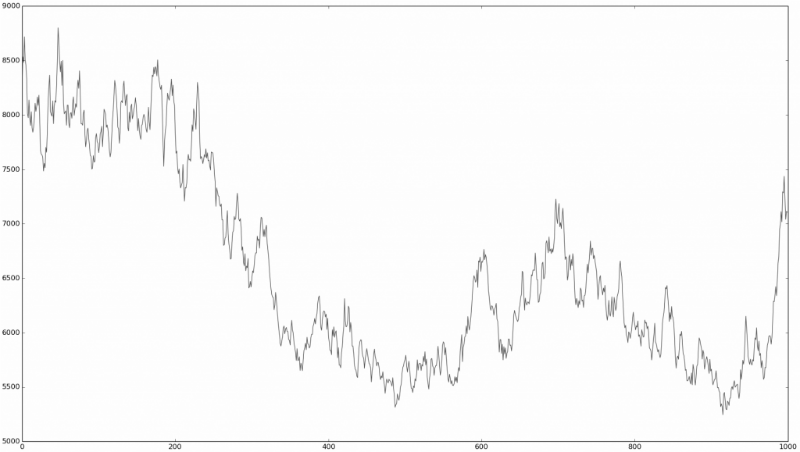
Или разницы вообще нет?

Это довольно трудно определить. Именно подобные наблюдения привели к тому, что многие исследователи в сфере финансовых рынков задумались о том, чтобы выяснить, насколько в действительно случайно поведение акций на бирже. Теория, которая говорит о том, что цены движутся случайным образом, получила название гипотезы случайного блуждания.

Многие из исследователей проводили тесты, подобные эксперименту Малкиеля, но на самом деле они не доказывают, что фондовый рынок развивается случайно. Они лишь доказывают, что для человеческого глаза, при отсутствии дополнительной информации, реальные движения цен невозможно отличить от случайных.

Есть недостатки и у самой гипотезы:

Она рассматривает разные рынки, как гомогенную среду, не учитывая различия между ними.
Она не объясняет многих эмпирических примеров, в которых люди постоянно выигрывали на рынке.
Она основа на статистическом определении случайности, а не на алгоритмическом. А это значит, что гипотеза не различает локальную и глобальную случайность, не учитывает концепцию относительности случайности.

И тем не менее, нравится это кому-то или нет, нельзя отрицать, что широкое распространение гипотезы случайного блуждания в среде количественных аналитиков на фондовом рынке в целом оказало серьезное влияние на то, как оцениваются различные финансовые инструменты — например, проивзодные инструменты или структурированные продукты.

Алгоритмическая vs статистическая случайность

Любая функция, вывод которой невозможно предсказать, является стохастической (случайной). И наборот, любая функция, чей вывод можно пердсказать, является детерминистической (не-случайной). Все усложняется тем, что многие детерминистические функции могут быть похожиме на стохастические. К примеру, большинство генераторов случайных числе на самом деле детерминистические функции, чей вывод яявляется стохастическим. Большинство генераторов случайных чисел на самом деле не случайны, поэтому их описывают с приставками псевдо- или квази-.

Для того, чтобы протестировать «валидность» гипотезы случайного блуждания, нужно определить, являются ли финансовые результаты той или иной акции (нашей функции) стохастическими или детерминистическими. Теоретически, существует алгоритмический и статистический подход к проблему, но на практике используются лишь последний (и тому есть объяснения).

Алгоритмический подход
Теория вычислимых функций также известная как теория рекурсии или вычислимость по Тьюрингу — это ветвь теоретической информатики, которая работает с концептом вычислимых и невычислимых функций. Функция называется вычислимой в зависимости от того, возможно ли написать алгоритм, который при наличии некоторых входных данных, всегда сможет ее вычислить.

Если случайность — это свойство непредсказуемости, то значит вывод функции никогда нельзя точно предсказать. Логически из этого вытекает, что всеслучайные процессы — это невычислимые функции, поскольку нельзя создать алгоритм для их вычисления. Знаменитый тезис Черча-Тьюринга постулирует, что функция вычислима, только если ее можно вычислить с помощью машины Тьюринга:

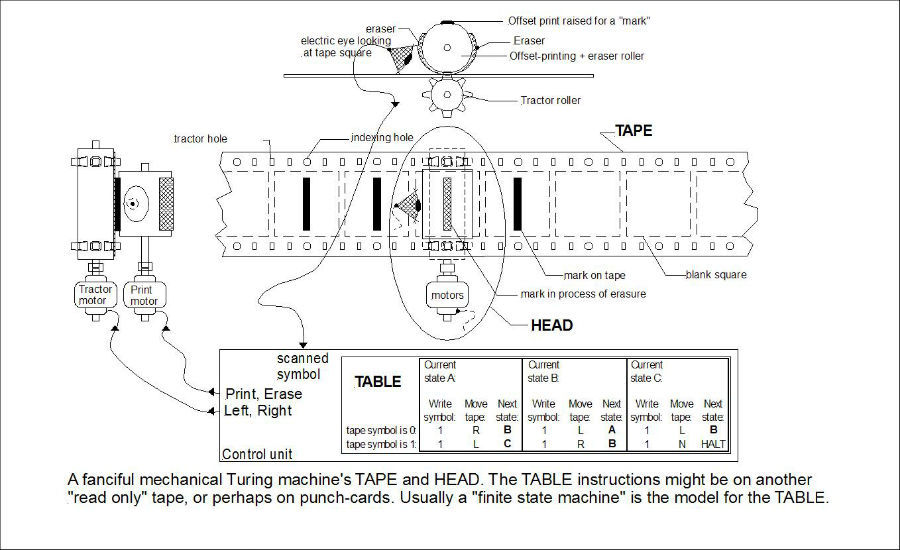
Казалось бы, все просто — нужно просто использовать машину Тьюринга для определения того, существует ли алгоритм, предсказывающие поведение цен акций (наша функция). Но здесь мы сталкиваемся с проблемой остановки, то есть задачей определения того, будет ли алгоритм работать вечно, или когда-нибудь он завершится.

Доказано, что эта проблема нерешаема, а значит невозможно заранее узнать, остановится ли программа, или продолжит работу. А значит, нельзя и решить проблему задачу поиска алгоритма, который может «вычислить» функцию (предсказать цену акции) — до остановки машине Тьюринга нужно будет перебрать все возможные алгоритмы, а это займет бесконечно много времени. Поэтому, невозможно и доказать, что финансовый рынок полностью случаен.

Если не принимать во внимание этот факт, то подобные изыскания привели к возникновению интересной области под названием алгоритмическая теория информации. Она имеет дело с отношениями между теорией вычислимости и теорией информации. Она определяет различные типа случайности — одним из самых популярных является определение случайности по Мартин-Лефу, согласн окоторому, для того, чтобы строка была признана случайной, она должна:

Быть несжимаемой — компрессия подразумевает поиск представления информации, которое использует меньше информации. К примеру, бесконечной длинная двоичная строка 0101010101…. может быть выражена более точно как 01, повторенное бесконечно много раз, в то время как бесконечно длинная строка 0110000101110110101… не имеет четко выраженного паттерна, а значит ее нельзя сжать до чего-либо короче, чем эта же самая строка 0110000101110110101… Это значит, что если Колмогоровская сложность больше или равна длина строки, тогда последовательность алгоритмически случайна.
Проходить статистические тесты на случайность — существует множество тестов на случайность, которые проверяют разницу между распределением последовательности относительно ожидаемого распределения любой последовательности, которая считается случайной.
Не приносить выгоду — интересный концепт, который подразумевает, что если возможно создать некую ставку, приводящую только к успеху, то значит она неслучайна.

В общем и целом, следует различать глобальное и локальное случайное блуждание. Первое относится к рынкам в долгосрочной перспективе, в то время как локальная гипотеза случайно блуждания может утверждать, что рынок случаен на протяжении некоторого минимального периода времени.

В отсутствии дополнительной информации многие системы могут казаться случайными не являясь таковыми — например, те же генераторы случайных чисел. Или, более сложный пример, движение цены некоторой акции может казаться случайным. Но если взглянуть на финансовые отчеты и другие фундаментальные индикаторы, то все может оказаться совсем неслучайным.

Статистический подход
Последовательность статистически случайна, когда она не содержит никаких выявляемых паттернов. Это не означает реальной случайности, то есть непредсказуемости — большинство псевдослучайных генераторов случайных чисел, которые не являются непредсказуемыми, при этом являются статистически случайными. Главное здесь — пройти набор тестов NIST. Большинство из этих тестов подразумевают проверку того, насколько распределение вывода предположительно случайной системы соответствует результатам действительно случайной системы. По ссылке представлен Python-код таких тестов.

Взламывая рынок

После обзора теоретических основ понятия случайности и рассмотрения тестов, которые позволяют ее выявить, другой важный вопрос заключается в том, можно ли с помощью таких тестов создать систему, которая будет определять случайность или неслучайность рыночных последовательностей лучше человека.

Исследователь решил провести собственный эксперимент, для которого использовал следующие данные:

Также анализировались активы различных типов:
Набор тестов NIST работал на наборах реальных данных — они дискретиризировались и разбивались на периоды 3,5,7 и 10 лет. Кроме того, существует два способа генерирования тестовых окон — накладывающиеся окна и ненакладывающиеся окна. Первый вариант лучше, поскольку позволяет видеть грядущую случайность рынка, но влияет на качество агрегированных P-значений, поскольку окна не независимы.

Кроме того, для сравнения использовалось два симулированных набора данных. Первый из них — набор двоичных данных, сгенерированный с помощью стратегии дискретизации алгоритма вихря Мерсенна (один из лучших псевдослучайных генераторов).

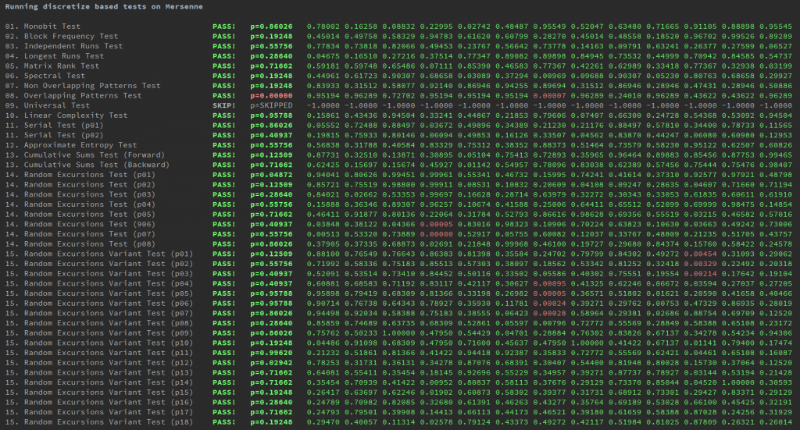
Второй — двоичные данные, сгенерированные функцией SIN.

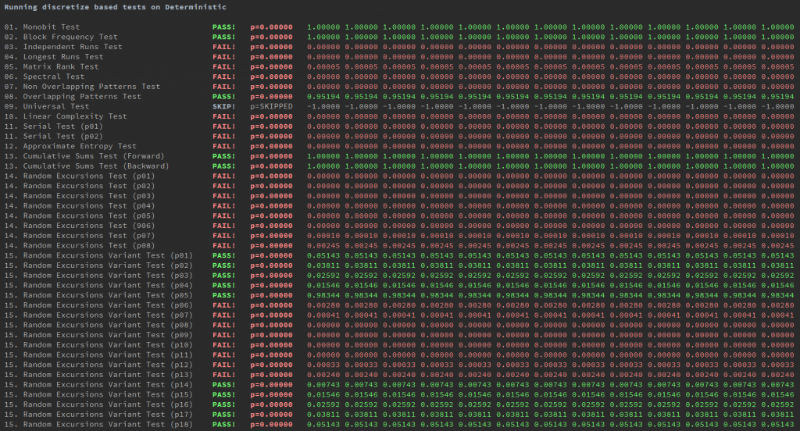
Проблемы

У каждого эксперимента есть свои слабые места. Не обошлось без них и в этот раз:

Для некоторых тестов требуется больше данных, чем сгенерировал рынок (кроме случаев использования минутных или тиковых графиков, что не всегда возможно), что значит, что их статистическая значимость чуть менее, чем идеальна.
Тесты NIST проверяют только стандартную случайность — это не значит, что рынки распределены не нормально или как-то по-другому, но все равно случайны.
Случайно выбранные временные периоды (начинающиеся с 1 января каждого года) и уровень значимости (0,005). Тесты нужно проводить на куда более обширном наборе выборок, которые начинаются с каждого месяца или квартала. P-значение не оказало серьезного влияния на итоговые выводы, поскольку при разных его значениях (0,001, 0,005, 0,05) некоторые тесты все равно не были пройдены в определенные периоды (например, 1954–1959 гг.)

Результаты

Вот каких результатов удалось добиться с помощью двух способов тестирования с накладывающимися или ненакладывающимися окнами:

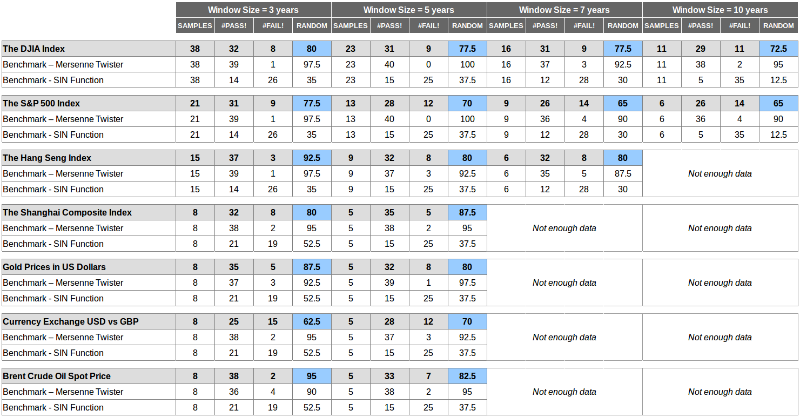
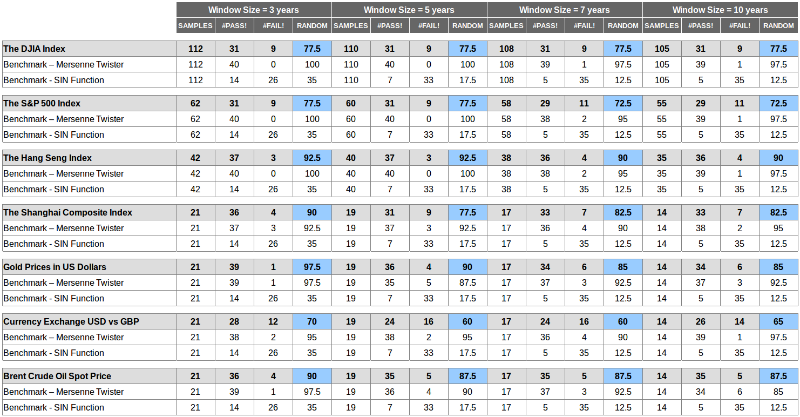
Выводы можно сделать следующие:

Значения лежат между значениями двух бенчмарков, что означает, что рынки менее случайны, чем вихрь Мерсенна и более случайны чем SIN-функция. Но в итоге они не случайны.
Значения серьезно различаются по измерению — размер окна серьезно влияет на результат, и уникальности — рынки не одинаково случайны, некоторые из них более случайны, чем другие.
Значения для бенчмарков консистентно хороши для вихря Мерсенна (в среднем пройдено более 90% тестов) и плохи для SIN-графа (пройдено в среднем 10–30% тестов).

В начале статьи мы рассматривали пример с экспериментом профессора Бертона Малкиеля, который написал знаменитую книгу «Случайное блуждание по Уолл-стрит» (A Random Walk Down Wall Street) — он представил случайное блуждание с помощью подбрасывания монетки и показал результаты чартисту. Когда чартист заявил, что «акцию» нужно покупать, профессиор Малкиель сравнил финансовый рынок с подбрасыванием монеты и использовал этот тезис для оправдания стратегии пассивных покупок и удержания позиций.

Однако автор текущего исследования считает, что подобный вывод ошибочен, поскольку эксперимент профессора говорит лишь о том, что с точки зрения чартиста, нет различия между подбрасыванием монеты и рынком. Однако с точки зрения количественных аналитиков и трейдеров или их алгоритмов это не очевидно. И проведенный с помощью набора тестов NIST эксперимент показал, что хоть и человеку бывает сложно отличить случайно сгенерированные данные от реальной финансовой информации, рынки на самом деле, далеко не случайны.