Duplo Railroad Tycoon: Синтез железнодорожной сети с максимальным покрытием17.01.2017 11:48

image

Детям Дед Мороз принес железную дорогу Duplo. Сегменты рельс очень легко соединяются между собой, и можно построить какой-нибудь небольшой, скорее всего просто замкнутый путь, поставить станцию и смотреть, как паровозик бегает по кругу. Иногда он останавливается и детёнок должен паровоз «заправить» из колонки, после чего паровоз снова поедет.

Вот пример простейшего пути:

image

Мне этот паровозик очень быстро наскучил, круга после третьего, и я пошел опять копаться на Thingiverse, чтобы в стотысячный раз попытаться применить 3Д принтер для чего-то полезного. И внезапно нахожу я там сегмент-стрелку как раз для паровоза Duplo.

Стрелка работает так: у нее есть три входа-выхода, назовем их первый, второй и третий. Если поезд въезжает в первый или второй узел, то он покидает стрелку всегда через третий. При этом стрелка переключается на соответствующий узел (т.е. если въехал через первый, то переключится на первый, если через второй — то на второй). А вот если он въезжает в третий узел, то выход зависит от состояния стрелки и он может выехать как через первый так и через второй. Т.е.:

'1' → '3' (стрелка переводится на '1')
'2' → '3' (стрелка переводится на '2')
'3' → если стрелка на '1', то '1', иначе '2'

Распечатал я таких стрелок парочку, и стал собирать «нормальную» железную дорогу. Только все получалось как-то уныло — паровоз ездил только по части пути, залипая на каком-нибудь кольце, и выезжать оттуда не желал.
Задачка первая (простая): Сколько должно быть сегментов-стрелок в сети, чтобы все узлы были связаны между собой?

Ответ
Стрелок должно быть обязательное четное число. Это легко понять, если мысленно представить два узла стрелки из трех соединенными между собой. То есть стрелка — это всегда плюс один свободный узел.

Но поднапрягшись, я для простейшего варианта задачу решил за несколько дней. Друг, пришедший в гости, решил ее за 5 минут, не напрягаясь :-).
Обозначим каждую стрелку буквой, узлы так же, как в примере выше. Т.е. в нашей сети есть узлы ['a1','a2','a3','b1','b2','b3'].
Решение
Для двух стрелок:
[('a1','a2'),('a3','b3'),('b1','b2')]
Так и только так поезд будет проезжать все сегменты дороги в разных направлениях. На самом деле для двух стрелок есть всего два варианта решения — вот этот и неправильный.

А что, если взять больше стрелок? Хм, если я над простым решением столько думал, то больше я явно не осилю. Но осилит компьютер! Только как вот к этой задаче подобраться? Я бился несолько дней, все пытаясь присобачить к этому какой-нибудь поиск в глубину, и уже почти все бросил, как вдруг мне пришла в голову идея написать решение на бумажке.

Я просто разбил весь трэк на шаги:
текущее состояние→переход по стрелке→переход по соединяющему сегменту→запомнить новое состояние стрелок

Т.е. для приведенного выше решения переходы будут такие (состояние стрелок по умолчанию: a3→ a1; b3→b1):
a1 → a3 → b3 (a3→ a1; b3→b1)
b3 → b1 → b2 (a3→a1; b3→b1)
b2 → b3 → a3 (a3→a1; b3→b2) ## обратите внимание, что стрелка b3 переключилась

Дальше просто:

  • Генерируем все возможные конфигурации дороги при заданном количестве стрелок
  • По каждой дороге:
    • Прогоняем поезд 10 раз и считаем количества проезда по каждому узлу
    • Если есть узлы с 0 или 1 проездом, то это значит система после выхода на режим свалилась в бесконечный цикл
    • Если таких узлов нет, значит поезд благополучно носится по всей дороге, что нам и надо!


Настолько просто, что я два дня бился головой об стол и пошел в итоге просить совета на stackoverflow, где мне выдали несолько решений на блюдечке за считанные минуты.

Генератор треков (объявлять задачей и убирать в спойлер не буду — для кого-то вроде меня это может быть очень жестокой шуткой, но попробуйте сами ради интереса решить): 

def getTrack(l):
    # recursion anchor, basic case:
    # when we have 2 nodes only one pair is possible
    if len(l) == 2:
        yield [tuple(l)]
    else:
        # Pair the first node with all the others
        for i in range(1, len(l)):
            # Current pair
            pair1 = [(l[0], l[i])]
            # Combine it with all pairs among the remaining nodes
            remaining = l[1:i] + l[i+1:]
            for otherPairs in getTrack2(remaining, 1):
                yield pair1 + otherPairs

Решалка треков: 

def solveTrack(track):
    #контейнер для считалки прохода по нодам с инициализацией
    nodeCount = {}
    for n in nodes:
        nodeCount[n] = 0         

    railTr = None
    jointTr = 'a1'

    while True:
        pos = jointTr   #текущая позиция
        nodeCount[pos] += 1 #посчитаем ее
        railTr = getTransition(track, pos) #переход по соединяющим рельсам (зависит только от конфигурации трека)
        nodeCount[railTr] += 1  #посчитаем этот узел тоже
        jointTr = tj[railTr] #переход по стрелке (зависит только от состояния стрелки, которое зависит от предыдущего прохода или начального состояния)
        if railTr[1] in ['1','2']: ##Перевести стрелку
            tj[railTr[0]+'3'] = railTr

        if max(nodeCount.values()) > nodesTrace and min(nodeCount.values()) < 3: #здесь мы просто после определенного числа прогонов nodesTrace смотрим, не осталось ли заброшенных участков. Если остались - значи поезд где-то залип и конфигурация не годится.
            #print "Infinite cycle detected"
            break
                
        #sol = "{}\t{}\t{}\t{}\t{}".format(pos, railTr, jointTr, tj['a3'], tj['b3'])
        #print sol
        if max(nodeCount.values()) > nodesTrace * 1.5:
            print "-------------------------------------------------------\n"
            print "Simulation complete!"
            print '\nNodes: ', nodeCount, "\n"
            print "Solution: ", track
            break
    return

Осталось только задать список узлов для входных данных, переходы между узлами стрелки и начинаем поиск решения! Ура! 

tj = {} #словарь переходов
nodes = [] #список узлов
##create joints transition table
for jt in range(nJoints):
    tj[idxs[jt]+'1'] = idxs[jt]+'3'
    tj[idxs[jt]+'2'] = idxs[jt]+'3'
    tj[idxs[jt]+'3'] = idxs[jt]+'1'
    nodes.extend((idxs[jt]+'1', idxs[jt]+'2', idxs[jt]+'3'))

Хм, а решения-то у дороги с четырьмя стрелками нет. И с шестью (я ждал несколько часов) — тоже нет. Вот и все. Мечте конец.
Хотя. А что, если сделать только часть стрелок переключаемыми, а остальные заморозить? Например, так: 
if railTr[0] in idxs[:nSwitchableJoints]: ## nSwitchableJoints - это количество переключаемых стрелок
            if railTr[1] in ['1','2']: ##Перевести стрелку
                  tj[railTr[0]+'3'] = railTr

И вуаля — решения есть и их много! Я постарался выбрать что-то покрасивее:-)
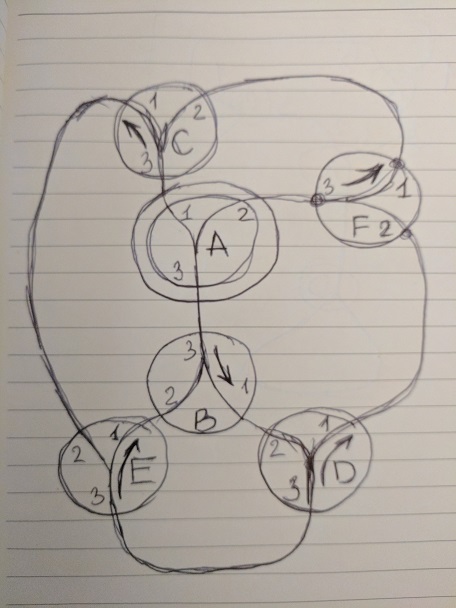
image
Здесь только стрелка 'а' — переключаемая, остальные тройку всегда разрешают в единицу.
Этот трек соответствует решению
[('a1', 'c3'), ('a2', 'f3'), ('a3', 'b3'), ('b1', 'd2'), ('b2', 'e1'), ('c1', 'e2'), ('c2', 'f1'), ('d1', 'f2'), ('d3', 'e3')]
nSwitchableJoints = 1

Вот и все, пока!

Комментарии (1)

  • 17 января 2017 в 10:12

    +3

    ↑

    ↓

    Молодец. Сразу понятно для кого железная дорога в действительности предназначалась ;)

© Habrahabr.ru