Дуальные числа в бизнесе или как оценить чувствительность решения к изменению начальных условий
За применение в бизнесе мнимых величин уже дали премию. Теперь интересно что-нибудь поиметь с дуальных.Дуальное число — это расширение поля действительных чисел (или любого другого, например комплексных) вида a + εb, где a и b — числа из исходного поля. При этом полагается, что ε ε = 0.Оказывается, у таких странных чисел есть практическое приложение.Основным полезным свойством дуальных чисел являетсяf (a + εb) = f (a) + εf'(a)b.Когда у нас есть формула для f (x), получить производную f'(x) труда не составит. Но часто f (x) доступно только в виде алгоритма — например как решение специальным образом составленной системы линейных уравнений. Запустив алгоритм с исходными данными, в которые добавлена ε мы получим результат и значение производной по одному из параметров.
Формально, дуальные числа образуют только кольцо, а не поле — очевидно, среди них есть делители нуля. Но если некоторая «хорошая» задача решается в действительных числах не вызывая деления на 0, то она же решится и в дуальных. По этому, в рамках этой статьи, пренебрежем математической строгостью и будем считать дуальные числа полем.Легко заметить, что коэффициенты при ε между собой ни когда не перемножаются — то есть они могут быть из произвольного модуля (векторного пространства) над исходным полем. В этом случае мы можем получить частные производные по нескольким аргументам.
Простые дуальные числа имеют матричное представление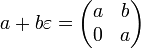 
. Для нашего обобщения матрица преобразуется в двухдиагональную, но при дальнейших операциях она превратится в треугольную. Коэффициенты над второй диагональю несут информацию об взаимодействии параметров — в некоторых задачах это может важной информацией, но сейчас мы будем ее игнорировать.Матричное представление интересно тем, что мы можем в задаче линейной алгебры «вписать» вместо исходного числа матричное представление дуального. Этот подход я глубоко не исследовал. Меня интересует случай, когда количество параметров сравнимо с размерностью задачи, а в этом случае сложность вычислений растет очень быстро. Преимуществом этого подхода является возможность использовать готовые высококачественные библиотеки линейной алгебры.
К сожалению, стандартные библиотеки основанные на BLAS и LAPAC работают только с действительными или комплексными числами. По этому я стал искать библиотеку, написанную на чистом Haskell — достаточно распространенном языке, в котором работать с разными представлении считается нормальным. Но меня ждало разочарование — единственные пакет, работающий с классом типов Floating (не понятно, почему не Fractional — синусы-косинусы в линейной алгебре не очень нужны), оказался linear. А самые интересные мне операции в нем реализованы только для матриц размеров до 4×4.Ради эксперимента я сделал простую реализацию дуальных чисел и примитивный решатель линейных уравнений, о которых хочу вкратце рассказать.Исходные тексты выложены здесь.
Тип данных для представления дуальных чисел описан так:
data GDual n v = ! n:± (v n) Параметрами его являются тип представления исходного поля и параметризованный контейнер для представления вектора ε. Неявно предполагается, что контейнер представляет класс типов Additive из пакета linear.Реализация Num достоточно тупа:
instance (Eq n, Num n, Additive v) => Num (GDual n v) where fromInteger x = (fromInteger x) :± zero (x1:± y1) + (x2:± y2) = (x1 + x2) :± (y1 ^+^ y2) (x1:± y1) — (x2:± y2) = (x1 — x2) :± (y1 ^-^ y2) (x1:± y1) * (x2:± y2) = (x1 * x2) :± ((y1 ^* x2) ^+^ (x1 *^ y2)) negate (x:± y) = (negate x) :± (y ^* (-1)) abs (a@(x:± y)) = case (signum x) of 0 → 0:± fmap abs y z → ((z * x) :± (x *^ y)) signum (x:± y) = case (signum x) of 0 → 0:± fmap signum y z → z:± zero Для abs и signum в окрестности нуля (0:± …) нарушается заявленное в классе типов соотношение abs x * signum x == x Но в других точках оно сохраняется.Реализация abs сделана так, что бы сохранялось соотношение f (a + εb) = f (a) + εf'(a)b где это возможно.Реализация Fractional:
instance (Num (GDual n v), Fractional n, Additive v) => Fractional (GDual n v) where (x1:± y1) / (x2:± y2) = (x1 / x2) :± ((y1 ^/ x2) ^-^ ((x1 / (x2 * x2)) *^ y2)) recip (x:± y) = (recip x) :± (y ^/ (x * x)) fromRational x = (fromRational x) :± zero Деление не совсем полноценное — оно не умеет делить на числа из окрестности нуля даже когда это возможно (класс типов Additive не предоставляет необходимой для этого функциональности). Но в моей области применения такого деления быть не должно — при вычислениях в обычных числах в этом случае случится деление 0/0.Реализация Floating, которую зачем-то захотел linear, тупа и приводить ее я не буду.Еще GDual реализует класс типов Epsilon из lianer с методом nearZero.
Math.GDual.Demo.SimpleSparseSolver.solve: (Fractional t1, Ord t, Epsilon t1) => [[(t, t1)]] → [[(t, t1)]] решает систему линейных уравнений, которая представлена прямоугольной разреженной матрицей. Матрица является конкатенацией матрицы коэффициентов и столбца правой части. solve элементарными операциями приводит матрицу к единичной — правая часть при этом превращается в ответ.Сессия ghci Prelude>: load Math.GDual.Demo.SimpleSparseSolver [1 of 1] Compiling Math.GDual.Demo.SimpleSparseSolver (Math/GDual/Demo/SimpleSparseSolver.hs, interpreted) Ok, modules loaded: Math.GDual.Demo.SimpleSparseSolver. *Math.GDual.Demo.SimpleSparseSolver>: load Math.GDual Ok, modules loaded: Math.GDual. Prelude Math.GDual>: add Math.GDual.Demo.SimpleSparseSolver [2 of 2] Compiling Math.GDual.Demo.SimpleSparseSolver (Math/GDual/Demo/SimpleSparseSolver.hs, interpreted) Ok, modules loaded: Math.GDual.Demo.SimpleSparseSolver, Math.GDual. *Math.GDual.Demo.SimpleSparseSolver> import Math.GDual *Math.GDual.Demo.SimpleSparseSolver Math.GDual> solve [[(0,1:± [1,0,0,0]),(1,2:± [0,1,0,0]),(2,3)],[(0,1:± [0,0,1,0]),(1,1:± [0,0,0,1]),(2,1)]] Loading package array-0.4.0.1 … linking … done. … Loading package linear-1.10.1.1 … linking … done. [[(2,-1.0+ε[-1.0,2.0,2.0,-4.0])],[(2,2.0+ε[1.0,-2.0,-1.0,2.0])]]
*Math.GDual.Demo.SimpleSparseSolver Math.GDual> import Linear *Math.GDual.Demo.SimpleSparseSolver Math.GDual Linear> inv22 $ V2 (V2 (1:± [1,0,0,0]) (2:± [0,1,0,0])) (V2 (1:± [0,0,1,0]) (1:± [0,0,0,1])) Just (V2 (V2 -1.0+ε[-1.0,1.0,2.0,-2.0] 2.0+ε[2.0,-1.0,-4.0,2.0]) (V2 1.0+ε[1.0,-1.0,-1.0,1.0] -1.0+ε[-2.0,1.0,2.0,-1.0]))
Производная функции показывает чувствительность значения функции к изменениям или ошибкам в параметрах. Но при этом ни как не учитываются ошибки округления в процессе вычисления функции. Эти ошибки может учесть другое обобщение чисел: интервальная арифметика
