Дистанционно-управляемый XY-манипулятор на базе кинематики H-bot

Картинка — Freepik: Maniacvector, Flaticon
Некоторое время назад, автору этой статьи пришла в голову своеобразная мысль:, а что если сделать удалённо-управляемый манипулятор, который может перемещаться по XY и совершать некую полезную работу?
Сказано — сделано, и работа закипела… В качестве основы для подобного манипулятора было решено взять широко известный принцип кинематики H-bot.
Сразу следует оговориться, что сам выбор подобной тематики для проработки, был осуществлён автором не случайно, так как уже упоминалось в предыдущих статьях, автор имеет ярко выраженную склонность к «выведению виртуала — в реал» и исключительно виртуальные вещи, вращающиеся где-то там далеко за экраном, не так интересны для автора.
В качестве ещё одного допущения, как следует относиться ко всему последующему тексту, следует отметить, что его нужно воспринимать больше как принцип (по управлению H-bot манипулятором), который можно реализовать на базе любой платформы, любого языка или любым иным способом, а не только описанным здесь. Тем не менее в самом конце статьи автор приложил свою реализацию концепции подобного управления, которую вы можете взять и использовать.
Использование подобной кинематики для управления человеком автором ещё нигде не наблюдалось (что, тем не менее, не исключает её наличия где-либо :-)))
В каком статусе находится подобная разработка в данный момент: практически реализована, однако, до момента окончательного запуска её, не будем о ней более подробно распространяться. Для чего она будет использована: для игры в настольный хоккей или футбол, в одной из школ. Для системы практически полностью напечатаны компоненты с использованием 3D принтера, а также она практически собрана (после ряда предварительных тестов).
Для чего ещё может быть применена подобная система: например, на той же стройке, для перемещения грузов в пределах строительной площадки и т.д.
Однако перейдём ближе к делу…
Существует целый ряд возможных кинематических решений, для перемещения целевой каретки в пределах координатной системы XY. Тем не менее автору приглянулась решение, носящее название H-bot:
Несмотря на ряд его недостатков, в числе которых возможность перекосов при движении, и ввиду этого, строгие требования к отсутствию люфтов, — автору подобное решение показалось достаточно простым и лаконичным, так как те же самые перекосы (при их возникновении), — вполне можно решать (программным или программно-аппаратным) путём.
А теперь попробуем прикинуть, каким образом можно было бы управлять подобным робототехническим приводом? Так как автор периодически возвращается в мыслях к идее стартапа, дающего возможность удалённого управления большими промышленными механизмами (например, экскаваторами, грейдерами и т.д. и т. п.), к примеру, чтобы сотрудники из одного региона, могли удалённо управлять устройствами, устроившись виртуально на работу в другом регионе («Скайнет» всё ближе, хе-хе), то, все технологии, которые могут облегчить реализации подобной затеи, вызывают повышенный интерес.
Здесь, конечно, возможно великое множество различных способов удалённого контроля, однако одним из наиболее простых и доступных (несмотря на то, что многие автора уверяли в том, что будет очень большой временной лаг и в реальном времени это будет невозможно, — эксперименты показали, что это не так) — является управление с использованием протокола MQTT.
Судя по информации, которую предоставляет один из известных MQTT-брокеров, среди его клиентов имеются известные компании, бренды которых у всех на слуху, не гнушающиеся использованием подобного протокола и этого брокера, для управления промышленными роботами в цеху. Соответственно, сделаем вывод, что и для нас это не грех.
Хотя одним из наиболее простых способов является управлением с помощью дискретных кнопок, автору захотелось реализовать более плавное управление, а здесь уже просится использование джойстика с отклоняемым стиком.
Долгий опыт работы со стиками, подобными показанному ниже, убедили автора в том, что чудес не бывает и любая механика рано или поздно изнашивается и начинает ощутимо «шуметь»:

Поэтому был выбран условно более надёжный способ, который заключается в использовании виртуального джойстика. Поверхностный анализ существующих решений выдал интересный вариант, который можно скачать с Google Play:
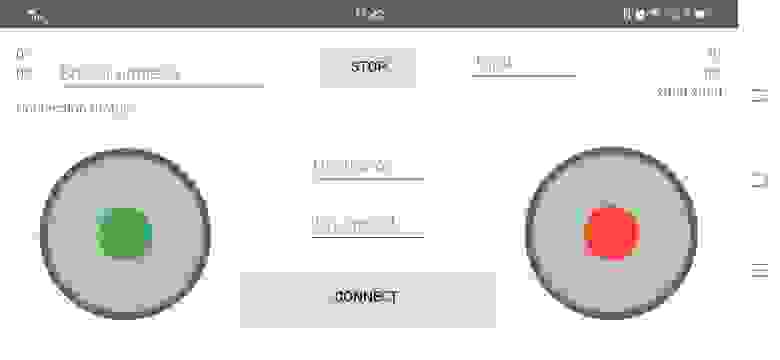
Конечно, джойстик нельзя назвать совершенным, так как, по сути, он содержит только два стика, а желательно, чтобы были ещё какие-либо функциональные кнопки, но, для описания концепции вполне годится (в любом случае при наличии интереса, вы сможете легко реализовать собственный джойстик, с собственным функционалом, либо скачать один из уже готовых вариантов, и управлять, используя другой протокол, как вариант).
Джойстик подключается к брокеру, и любое перемещение каждого из стиков вызывает передачу в нужный топик брокера двух цифр разделённых пробелом. Например, для левого стика, передаваемые цифры вы можете увидеть в верхней левой части джойстика, а для правого, соответственно, в правой верхней части.
Например, на принтскрине ниже показано, как меняются цифры, для левого джойстика, если нажать на его центральную зону и перетащить этот шарик куда-либо. Первая цифра показывает, соответственно, угол наклона стика, а вторая цифра показывает степень дальности шарика от центра стика. Другими словами, первая цифра показывает, «в каком направлении мы едем», а вторая цифра показывает «с какой скоростью мы едем»:

Если мы ещё раз обратимся к логике кинематики H-bot, то мы увидим, что в составе подобной схемы, из механики используются два двигателя. Так как человечество ещё ничего принципиально более нового и совершенного не изобрело для управления двигателями, кроме ШИМ-контроля (хотя, учитывая технический прогресс, автор уже ни в чём не уверен :-))), то и мы будем использовать этот же подход.
Разрешение ШИМ-сигнала будем использовать восьмибитное, то есть, другими словами, дающее 256 градаций значения скорости. Теоретически можно было бы использовать и большее разрешение, но в дальнейшем могут возникнуть проблемы с его реализацией (с аппаратной поддержкой), да и к тому же — подобное разрешение видится вполне достаточным (спорно, согласен).
Теперь, с учётом всего вышеизложенного, а также после того как мы ознакомились с логикой H-bot, попробуем нанести на круговую схему, — как направления вращения двигателей, так и требуемые для этого углы.
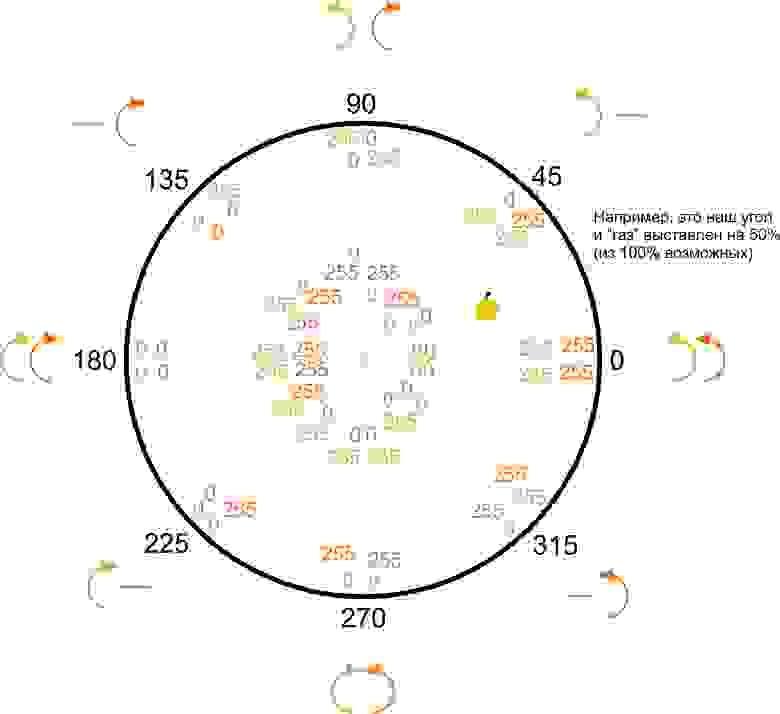
На картинке двумя разными цветами показаны два двигателя и направление их вращения для реализации упомянутой выше кинематики. Символ в виде горизонтальной линии показывает, что двигатель в этот момент не работает. Также можно заметить, что отмечены только восемь углов. Однако, это совершенно не значит, что двигатели имеют скачкообразные изменения скорости только при этих значениях. Скорость двигателя может плавно расти или увеличиваться в определённом интервале.
Например, если мы обратимся к интервалу 0–45° (в финальной программе интервал 0–44° и т.д., то есть, на одно значение меньше в каждом интервале), то можно увидеть, например, что в этом интервале скорость правого двигателя плавно убавляется и, с 45° и вплоть до 89°- скорость правого двигателя плавно нарастает, инвертированная по направлению в другую сторону.
Цифры внутри круга показывают, какое цифровое значение ШИМ-управления вращения двигателя является максимальным, а какое минимальным. Не забываем, что при инвертировании направления вращения меняется также и диапазон чисел. Например, если мы обратимся к интервалу от 0 до 45° (на картинке выше), то там можно увидеть, что для правого двигателя минимальным значением является 0, а максимальным 255.
Однако, если мы обратимся опять же к правому двигателю, в интервале от 45 до 90°, мы заметим, что для него диапазон значений ШИМ инвертировался также в противоположную сторону, и для него теперь в этом положении максимальным значением становится 0, а минимальным 255 и т.д.
Теперь, когда у нас есть понимание работы всей системы в целом, мы можем реализовать изложенные идеи в программном коде. Одним из наиболее простых способов видится использование C++ и её функции map, которая позволяет пропорционально перенести значение из одного диапазона в другой, так как нам требуется перевести угол наклона и силу «газа» в конкретные значения ШИМ целевого двигателя.
Синтаксис функции выглядит следующим образом:
map(value, fromLow, fromHigh, toLow, toHigh)
value: значение для переноса
fromLow: нижняя граница текущего диапазона
fromHigh: верхняя граница текущего диапазона
toLow: нижняя граница нового диапазона, в который переносится значение
toHigh: верхняя граница нового диапазона
Как можно было заметить по картинке намного выше, на каждом из диапазонов углов, скорость одного из двигателей является постоянной, а скорость другого двигателя изменяется. Таким образом, напрашивается управление скоростью одного двигателя с использованием степени удаления пальца от центра джойстика, а скоростью другого двигателя — углом наклона (дополнительную корректировку скорости одного из двигателей, скорость которого зависит от угла наклона — ещё и установить в зависимость от удалённости пальца от центра решил не делать, так как будет слегка заморочено, и даже существующая схема вполне должна работать).
Таким образом, с учётом всего вышеизложенного, функция, управляющая скоростями двигателей, будет выглядеть следующим образом:
void Motors_Control (int ugol,int PWM)
{
if (PWM != 0)
{
if (ugol != ugol_current)
{
//записали текущее значение угла
//для чего это надо: будем теперь менять скорость,
//только если пришла новая цифра значения угла - которая отличается
//от текущего(т.к. с брокера приходит непрерывная череда цифр,
//которые могут быть одинаковыми, если вы удерживаете джойстик в одном
//положении, нам надо реагировать только на отличающиеся):
ugol_current = ugol;
//
if ( (ugol>=0)&&(ugol<=44) )
{
//вычисляем скорость левого двигателя
int left_motor_PWM = map(PWM, 0, 100, PWM_min, PWM_max);
//вычисляем скорость правого двигателя
//тут 0-мин.скорость, 255- макс.скорость
int right_motor_PWM = map(ugol, 0, 44, PWM_max, PWM_min) ;
Left_Motor (false, left_motor_PWM);
Right_Motor (false, right_motor_PWM);
}
else if ( (ugol>=45)&&(ugol<=89) )
{
//вычисляем скорость левого двигателя
int left_motor_PWM = map(PWM, 0, 100, PWM_min, PWM_max);
//вычисляем скорость правого двигателя
//тут 255-мин.скорость, 0- макс.скорость
int right_motor_PWM = map(ugol, 45, 89, PWM_max, PWM_min);
Left_Motor (false, left_motor_PWM);
Right_Motor (true, right_motor_PWM);
}
else if ( (ugol>=90)&&(ugol<=134) )
{
//вычисляем скорость правого двигателя
int right_motor_PWM = map(PWM, 0, 100, PWM_max, PWM_min);
//вычисляем скорость левого двигателя
//тут 0-мин.скорость, 255- макс.скорость
int left_motor_PWM = map(ugol, 90, 134, PWM_min, PWM_max);
Left_Motor (false, left_motor_PWM);
Right_Motor (true, right_motor_PWM);
}
else if ( (ugol>=135)&&(ugol<=179) )
{
//вычисляем скорость правого двигателя
int right_motor_PWM = map(PWM, 0, 100, PWM_max, PWM_min);
//вычисляем скорость левого двигателя
//тут 255-мин.скорость, 0- макс.скорость
int left_motor_PWM = map(ugol, 135, 179, PWM_max, PWM_min);
Left_Motor (true, left_motor_PWM);
Right_Motor (true, right_motor_PWM);
}
else if ( (ugol>=180)&&(ugol<=224) )
{
//вычисляем скорость левого двигателя
int left_motor_PWM = map(PWM, 0, 100, PWM_max, PWM_min);
//вычисляем скорость правого двигателя
//тут 255-мин.скорость, 0- макс.скорость
int right_motor_PWM = map(ugol, 180, 224, PWM_max, PWM_min);
Left_Motor (true, left_motor_PWM);
Right_Motor (true, right_motor_PWM);
}
else if ( (ugol>=225)&&(ugol<=269) )
{
//вычисляем скорость левого двигателя
int left_motor_PWM = map(PWM, 0, 100, PWM_max, PWM_min);
//вычисляем скорость правого двигателя
//тут 0-мин.скорость, 255- макс.скорость
int right_motor_PWM = map(ugol, 225, 269, PWM_min, PWM_max);
Left_Motor (true, left_motor_PWM);
Right_Motor (false, right_motor_PWM);
}
else if ( (ugol>=270)&&(ugol<=314) )
{
//вычисляем скорость правого двигателя
int right_motor_PWM = map(PWM, 0, 100, PWM_min, PWM_max);
//вычисляем скорость левого двигателя
//тут 255-мин.скорость, 0- макс.скорость
int left_motor_PWM = map(ugol, 270, 314, PWM_max, PWM_min);
Left_Motor (true, left_motor_PWM);
Right_Motor (false, right_motor_PWM);
}
else if ( (ugol>=315)&&(ugol<=359) )
{
//вычисляем скорость правого двигателя
int right_motor_PWM = map(PWM, 0, 100, PWM_min, PWM_max);
//вычисляем скорость левого двигателя
//тут 0-мин.скорость, 255- макс.скорость
int left_motor_PWM = map(ugol, 315, 359, PWM_min, PWM_max);
Left_Motor (false, left_motor_PWM);
Right_Motor (false, right_motor_PWM);
}
}
}
else
{
Stop ();
}
}
В коде выше: PWM_min = 0; PWM_max = 255; true или false — передающиеся в подфункции, непосредственно связанные с двигателями — управляют прямым или обратным направлением вращения.
В свою очередь, эта функция будет вызываться внутри другой, которая будет осуществлять первичный парсинг сообщения, полученного в виде строки с брокера, и выдёргивать из неё две требующиеся цифры:
void Motors (char* topic, char ch [])
{
//строка, куда мы записали название топика,
//которое ниже будем анализировать
String s = topic;
//преобразовали массив символов - в строку
String s2 = String(ch);
// Serial.println (s2);
//Выдернули из строки только её кусок - с первой цифрой,
//для этого - нашли, на какой позиции (т.е. номер) стоит пробел в этой строке
String s3 = s2.substring (0, s2.indexOf(" "));
//Преобразовали выдернутый кусок строки - в число
//(т.к. компьютер понимает пока этот кусок как строку,
//он не знает что это число. Ему надо явно "пальцем показать")
int ugol = s3.toInt();
// Serial.println (motor_direction);
//Выдернули из строки только её кусок - со второй цифрой,
//для этого - нашли, на какой позиции (т.е. номер) стоит пробел в этой строке
String s4 = s2.substring (s2.indexOf(" "), s2.length());
//Преобразовали выдернутый кусок строки - в число
//(т.к. компьютер понимает пока этот кусок как строку,
//он не знает что это число. Ему надо явно "пальцем показать")
int motor_PWM = s4.toInt();
// Serial.println (motor_PWM);
// Serial.println ( motor_direction );
//теперь у нас есть 2 выдернутые цифры
//и теперь мы вызываем функцию, которая запустит двигатели нужным образом
//(и в эту функцию мы передаём полученные 2 цифры):
Motors_Control (ugol, motor_PWM);
}
Таким образом, на выходе получится достаточно интересная вещь, позволяющая с джойстика управлять искомым манипулятором типа H-bot.
Полный код подобного управления для манипулятора, реализации автора, можно скачать здесь.
Если хорошо подумать, для подобного манипулятора может быть найдено множество полезных применений:
- переноска тяжестей в пределах строительной площадки;
- рисование картин на больших высотах, художником, стоящим на земле;
- оштукатуривание и подкраска участков стен на больших высотах;
- настольная игра (в данный момент реализуется автором);
- и так далее.
По крайней мере, использование такого манипулятора подобным неожиданным образом, а не только в 3D-принтерах/ЧПУ-станках видится достаточно любопытным…
В версии автора статьи к каретке будет ещё прикреплён сервопривод, на конце которого будет находиться двигатель с крыльчаткой, наносящей удар по мячу:
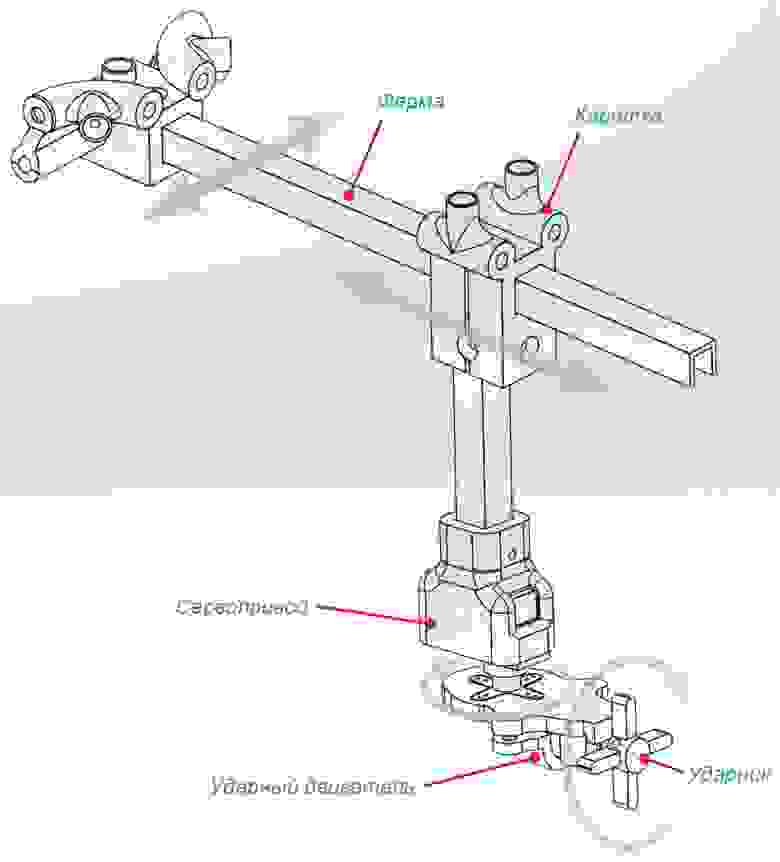
Как альтернатива этому — установить бьющий соленоид, и сделать из всей этой истории — бильярд :-).
Соответственно, код будет тоже доработан под эти элементы в будущем.
Играй в нашу новую игру прямо в Telegram!

