Делаем маршрутизацию (роутинг) на OpenStreetMap. Добавляем поддержку односторонних дорог
Продолжаем цикл статей про построение систем роутинга со сложными требованиями на основе Open Source базы данных PostgreSQL и расширения PgRouting на карте OpenStreetMap. Сегодня мы поговорим о том, как добавить поддержку односторонних дорог (направлений движения). Зачастую, именно отсутствие этой поддержки является основной причиной смены PgRouting на другой «движок» маршрутизации. Как обычно, все данные и результаты доступны в моем GitHub репозитории OSM Routing Tricks, который я пополняю по мере публикаций.
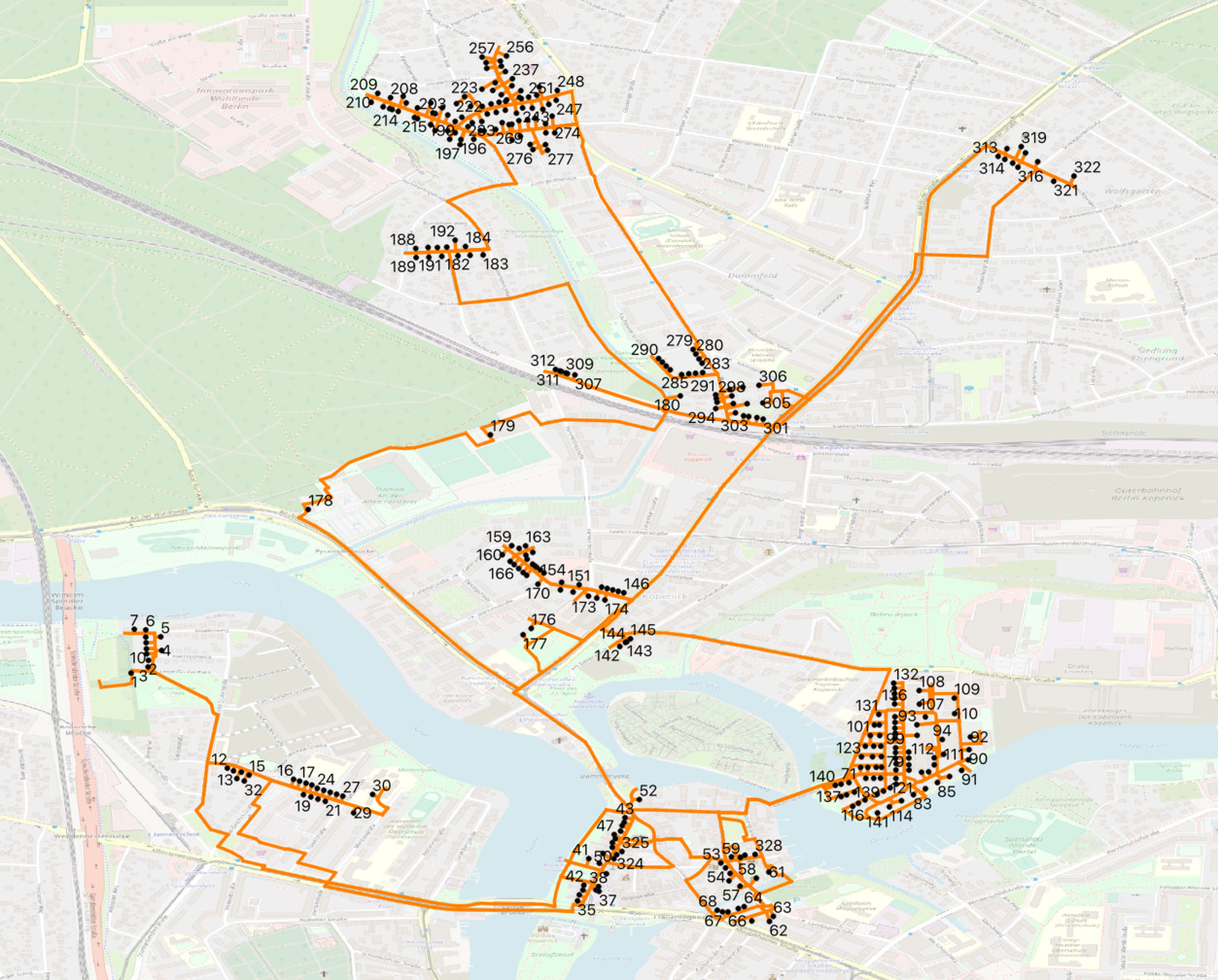
Небольшой маршрут из 330 адресов на карте OpenStreetMap.
Что такое односторонние дороги и зачем они нужны
В первую очередь, мы говорим об односторонних дорогах на карте, то есть таких, по которым движение разрешено только в одну сторону. Разумеется, двигаться по ним в другую сторону запрещено. Особенно часто такое ограничение встречается на мостах, в туннелях и на высокоскоростных шоссе, где движение в противоположную сторону опасно для жизни. Разумеется, нам необходимо соблюдать направление движения для автотранспортных средств, здесь не может быть компромиссов. В то же время, для пешеходного роутинга это не является обязательным, хотя и удобно двигаться по маршруту по направлению движения автомобилей — проще ориентироваться, можно воспользоваться общественным транспортом или такси и т.п. Замечу, что некоторые (многие, на самом деле) открытые системы роутинга игнорируют это правило, то есть они подразумевают пешеходный роутинг (по пешеходным дорогам и по окружающим не пешеходные дороги тротуарам, которые могут и отсутствовать в действительности), независимо от длины маршрута и наличия тротуаров в туннелях и на скоростных шоссе.
Кроме того, поддержка односторонних дорог позволяет улучшить маршрутную сеть — заданные направления движения заметно упрощают поиск оптимального маршрута за счет очень значительного снижения количества возможных вариантов, можно учесть рельеф местности (довольно трудно с грузом или без подняться по множеству ступенек крутой лестницы, особенно, если можно вместо того спускаться по ней) и принудительно сделать некоторые участки односторонними, можно сделать односторонними виртуальные соединения между домами и улицами (так что маршрут будет построен с последовательной нумерацией, даже если он несколько раз проходит по одной улице — поскольку длина маршрута в таком случае не меняется, сам PgRouting никак не гарантирует, что все адреса на такой улице будут посещены в один и тот же проход по ней). И так далее, есть еще много возможностей, доступных для роутинга с поддержкой направлений движения.
Добавляем поддержку односторонних дорог в PgRouting
Официальная документация PgRouting для функции pgr_TSP — Using Simulated Annealing approximation algorithm сообщает нам:
If using directed:= true, the resulting non symmetric matrix must be converted to symmetric by fixing the non symmetric values according to your application needs.
Отлично, но в документации нет ни слова о том, как это сделать. Нам придется начать с теории и разобраться, возможно ли это и как именно это сделать. Англоязычная страница википедии, посвященная проблеме коммивояжера, содержит нужный нам раздел Travelling salesman problem: Asymmetric:
Solving an asymmetric TSP graph can be somewhat complex. The following is a 3×3 matrix containing all possible path weights between the nodes A, B and C. One option is to turn an asymmetric matrix of size N into a symmetric matrix of size 2N.
Здесь сказано, что решение задачи коммивояжера на асимметричной матрице расстояний усложняется, поэтому лучше превратить асимметричную матрицу в симметричную (ценой удвоения размера матрицы) и решать более простую симметричную задачу на симметричной матрице расстояний. Почти то же самое, что и в документации PgRouting, зато здесь объяснено, зачем же нужна именно симметричная матрица. Далее на этой же викистранице приводится алгоритм конвертации асимметричной матрицы в симметричную и пример конвертации простой матрицы. Идея простая — каждый узел и каждое ребро заменить на два и задать такую матрицу расстояний между ними, чтобы полученный на такой матрице путь соответствовал искомому. Ниже мы рассмотрим этот пример из вики. К сожалению, графическое представление соответствующего графа я рисовал на листочках от руки и показать здесь не могу (почерк у меня как у физика, так что извините).
Пусть у нас задана асимметричная матрица весов:
Ей соответствует следующая симметричная матрица весов:
где -w это виртуальные соединения для виртуальных узлов, которые рекомендуется задать некоторым отрицательным числом, потому что
w=0 is not always low enough
Теперь мы можем написать соответствующую функцию-обертку для PgRouting. Поскольку PgRouting отбрасывает все отрицательные значения в матрице весов, мы используем нулевое значение (мы это компенсируем заданием очень высоких весов для запрещенных направлений) и добавляем еще [избыточные] ребра с очень высоким весом, поскольку PgRouting требует указания весов между всеми узлами матрицы (в теории этого не требуется, это просто техническое ограничение, которому нам приходится соответствовать).
CREATE OR REPLACE FUNCTION pgr_dijkstraSymmetrizeCostMatrix(matrix_cell_sql text,
OUT start_vid BIGINT, OUT end_vid BIGINT, OUT agg_cost float)
RETURNS SETOF RECORD AS
$BODY$
DECLARE
sql text;
r record;
BEGIN
sql := 'with edges as (' || matrix_cell_sql || ')
select 3e9+start_vid as start_vid, end_vid as end_vid, agg_cost from edges
union
select end_vid, 3e9+start_vid, agg_cost from edges
union
select 3e9+start_vid, start_vid, 0 from edges
union
select start_vid, 3e9+start_vid, 0 from edges
union
select start_vid, end_vid, 1e6 from edges
union
select 3e9+start_vid, 3e9+end_vid, 1e6 from edges
';
FOR r IN EXECUTE sql LOOP
start_vid := r.start_vid;
end_vid := r.end_vid;
agg_cost := r.agg_cost;
RETURN NEXT;
END LOOP;
END;
$BODY$
LANGUAGE plpgsql VOLATILE STRICT;Однако, этого недостаточно. Дело в том, что PgRouting требует указания всех весов, а у нас в исходной матрице весов часть значений может быть пропущено, что приводит к ошибке роутинга
An Infinity value was found on the Matrix
Заполним все значения матрицы весов с помощью еще одной функции-обертки (можно было бы упростить pgr_dijkstraSymmetrizeCostMatrix () и не добавлять в ней избыточные ребра, но в таком случае при полной исходной матрице мы получим не полную итоговую матрицу, что, на мой взгляд, не есть правильно):
CREATE OR REPLACE FUNCTION pgr_dijkstraValidateCostMatrix(matrix_cell_sql text,
OUT start_vid BIGINT, OUT end_vid BIGINT, OUT agg_cost float)
RETURNS SETOF RECORD AS
$BODY$
DECLARE
sql text;
r record;
BEGIN
sql := 'WITH RECURSIVE src AS (' || matrix_cell_sql || '),
dst AS (
select
*
from src where start_vid =
(select
start_vid
from src
group by start_vid
order by count(*) desc
limit 1)
union
select
src.*
from src, dst
where src.start_vid=dst.end_vid
)
select * from dst';
FOR r IN EXECUTE sql LOOP
start_vid := r.start_vid;
end_vid := r.end_vid;
agg_cost := r.agg_cost;
RETURN NEXT;
END LOOP;
END;
$BODY$
LANGUAGE plpgsql VOLATILE STRICT;Теперь мы учли все требования PgRouting и можем работать с односторонними дорогами. Отмечу, что полученные обертки можно использовать и для симметричной матрицы, когда априори не известно, будет ли исходная матрица симметричной (хотя для симметричной исходной матрицы это приведет к не нужному ее увеличению и замедлению обработки).
Исходные данные
Мы используем все те же данные, что и в предыдущей части статьи плюс определенные выше дополнительные функции. Несколько расширенный скрипт load.sh из репозитория загрузит в базу данных PostgreSQL все необходимое.
Поиск оптимального маршрута для автомобиля
Поскольку для пешехода тротуары доступны в любом направлении, а для автомобиля одностонние дороги доступны лишь в одном направлении, необходимо указывать разные весовые функции для роутинга пешеходного и автомобильного. Как уже упоминалось ранее, наша дорожная сеть оптимизирована для автомобильного роутинга, о нем и поговорим. Итак, запретим (укажем очень большую длину миллион метров) движение в противоположном направлении. Ранее при подготовке дорожной сети мы разделили каждую дорогу на две, одна из которых (type='osm') совпадает с исходной и вторая (type='osmreverse') инвертирована. Соответственно, для односторонней дороги добавленная нами ее инвертированная копия должна быть запрещена для любого движения (вообще говоря, можно ее и вовсе не создавать, но тогда будет немного сложнее объяснить построение дорожной сети). Кроме того, для прямого движения должна быть доступна только исходная дорога (type='osm') и для обратного — инвертированная (type='osmreverse'). В таком случае, итоговые прямая и обратная весовые функции имеют вид:
case when (type='osmreverse' and oneway) then 1000000 else length end as cost,
case when type ilike 'osm%' then 1000000 else length end as reverse_cost,где length — геометрическая длина соответствующего сегмента дороги. Усложнив дорожную сеть (заранее исключив ненужные сегменты), можно взамен упростить весовые функции.
Построим оптимальный маршрут все для тех же случайных 330 адресов домов и с помощью функции PgRouting pgr_TSP () и добавленных выше функций pgr_dijkstraSymmetrizeCostMatrix () и pgr_dijkstraValidateCostMatrix (). Теперь мы можем использовать флаг directed=true, так как теперь мы добавили для pgr_TSP () поддержку односторонних дорог (точнее, симметризацию и заполнение пропущенных значений в несимметричной матрице, которая получается при наличии односторонних дорог). Как и ранее, в результате выполнения немного модифицированного SQL скрипта route.sql создается таблица «route» с сегментами маршрута для каждого заданного адреса, которую можно визуализировать с помощью программы QGIS. Файл проекта QGIS тоже обновлен, см. в репозитории route.qgs Полученная карта с маршрутом представлена на картинке до хабраката.
Смотрите на следующем рисунке участок построенного маршрута с порядковыми номерами посещенных домов (здесь черным цветом обведены односторонние дороги):

Проверим, что теперь по односторонним улицам движение выполняется только одну сторону и, притом, в требуемом направлении. Вот карта OpenStreetMap, на которой стрелками указаны направления движения по односторонним дорогам:

Как и указано на карте OpenStreetMap, в построенном маршруте движение выполняется слева направо для участка дороги с пунктами маршрута 329,330,331 на левой стороне дороги:
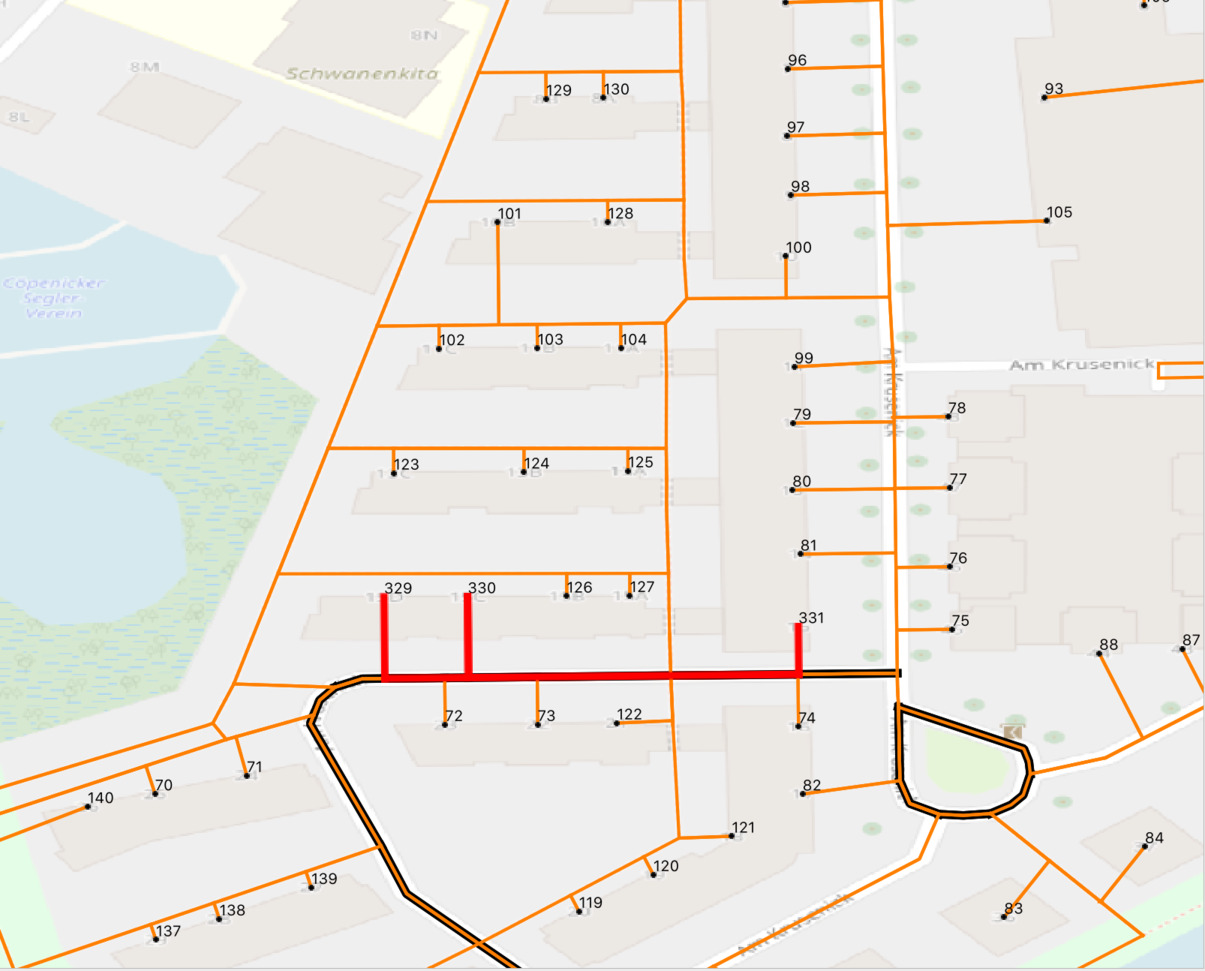
и в том же направлении (слева направо) для участка дороги с пунктами маршрута 72,73,74 на правой стороне дороги (второй проход по этому участку дороги):
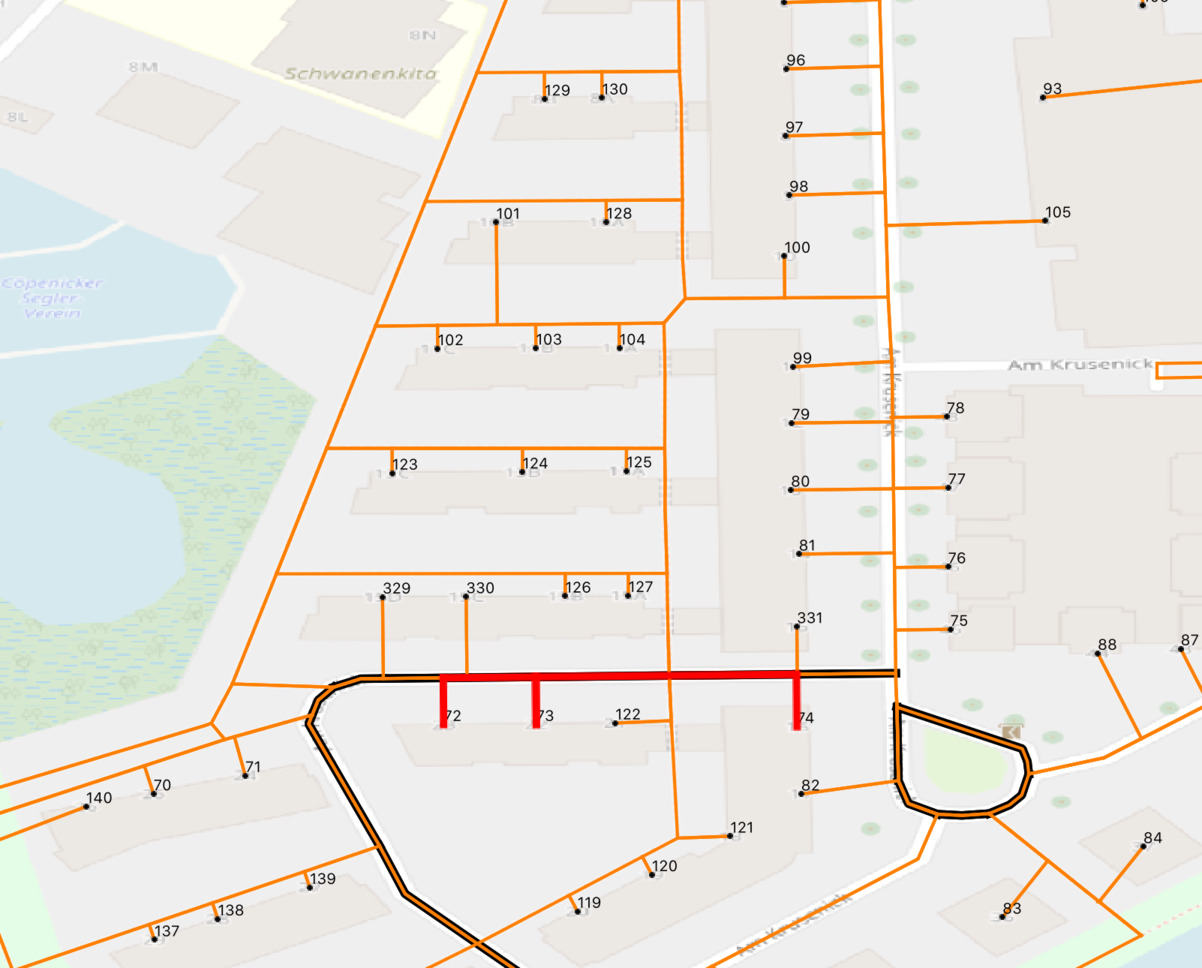
Нумерация домов по сторонам улиц между перекрестками последовательная. Зачастую нумерация последовательная и после перекрестков (см. картинки выше). Таким образом, мы добились заметного улучшения качества маршрута, не меняя дорожную сеть и не занимаясь оптимизацией параметров функции pgr_TSP ().
Что касается времени, затраченного на построение маршрута, оно увеличилось примерно втрое за счет добавления функций-оберток для поддержки односторонних дорог. Это было ожидаемо из-за увеличения матрицы весов.
Заключение
В этой статье мы улучшили возможности PgRouting, добавив к нему несколько своих функций. Теперь мы можем двигаться по дорогам в правильном направлении, что необходимо для построения реальных маршрутов и позволяет значительно улучшить итоговый маршрут, поскольку при этом количество возможных маршрутов кардинально снижается.
Если рассмотреть весь маршрут детально, то его еще можно улучшить, в том числе, с помощью оптимизации параметров функции pgr_TSP (). Но дело в том, что только путем оптимизации этих параметров подобного полученному выше результату добиться не удастся — в самом деле, алгоритм оптимизации маршрутов PgRouting ничего «не знает» про наши предпочтения о последовательной нумерации и другие. Так что поддержка односторонних дорог, на самом деле, дает нам намного больше, чем можно было бы ожидать.
Можно ли добиться аналогичного результата с последовательной нумерацией зданий между перекрестками иначе, не увеличивая матрицу весов с соответствующим замедлением построения маршрута? Да, можно. Более того, можно еще и значительно ускорить построение маршрута (например, на один-два десятичных порядка), в том числе, с учетом односторонних дорог. Об этом мы и поговорим в следующий раз.
