Что такое квантовая запутанность
Я хочу поговорить о таком явления. Это явление можно рассматривать на двух уровнях понимания. Первый уровень понимания описательный — что же происходит такого необычного в эксперименте с квантовой запутанностью. Этот уровень не требует понимания квантовой механики, не требует знания его уравнений, операторов волновых функций и прочих инструментов. Он требует лишь общих знаний — что такое косинус, вероятность, вектор. Второй уровень понимания — это интерпретация, она объясняет, как это происходит на глубоком физическом уровне материи, здесь конечно без знания физики в целом и квантовой механики не обойтись. Да и этого может быть недостаточно, отсюда и принцип работы «заткнись и считай». Но я хочу остановиться именно на первом описательном уровне понимания. Что же здесь происходит такого странного и необычного, что называется квантовая запутанность?
Я прочитал и просмотрел большое количество материалов, в которых было описание этого явления, и попытка показать, что в экспериментах с квантовой запутанностью происходит нечто необычное для привычной реальности. Но, честно говоря, во всех материалах предлагаемые аргументы мне показались неубедительными. Наиболее удачным описанием эксперимента мне показалась лекция Михаила Осокина о неравенстве Белла. Для упрощения объяснения, он рассматривает не противофазную систему, которая возникает в экспериментах с квантовой запутанностью, а синфазную, то есть гипотетический эксперимент, где возникают полные синфазные клоны-частицы с одинаковыми свойствами. Для объяснения самого явления это не принципиально. Если удастся объяснить явление с синфазными частицами, то несложно построить аналогичное объяснение с противофазными частицами. Для удобства я так же как и Михаил Осокин буду рассматривать синфазные частицы, а не противофазные.
Давайте, я начну процесс осмысления в форме диалога двух оппонентов. Один из них — Докладчик, приводит аргументы, описывающие эксперимент с квантовой запутанностью синфазных частиц, и пытается убедить, что здесь происходит нечто необычное. Другой — Слушатель, критически мыслящий человек опровергает эти аргументы, если они неубедительные. Цель такого диалога — вынудить Докладчика предъявить такие аргументы, которые нельзя опровергнуть, нельзя объяснить полученный результат без введения понятия квантовой запутанности. В этот момент и появляется первое понимание этого явления. Итак, начнем.
Докладчик:
— Есть такое понятие спин, не вдаваясь в его физическую суть, просто скажем, что это свойство частицы, которое можно определить либо как +1 либо как -1. Но прежде чем выяснить это свойство, необходимо выбрать ориентацию детектора в пространстве каким-либо образом. Детектирование, при этом, возможно изменяет спин, если он до измерения не был определён в том же направлении. При измерении двух запутанных частиц-клонов детекторами, ориентированными в одном направлении в пространстве, эксперимент всегда даёт одинаковые (противоположные для противофазной системы) спины.
Слушатель:
— И что здесь удивительного? Представьте, я взял два шарика от пинг-понга, раскрасил половинки чёрным цветом и расположил два шарика, одинаково. Если вы возьмёте любое направление в пространстве, и посмотрите на точку шарика, которая смотрит в этом направлении, то эти точки на двух шариках всегда будут иметь одинаковые цвета. Это и есть квантовая запутанность шариков от пинг-понга? Ничего тут странного не вижу. Аргумент ваш неубедительный.
Докладчик:
— Хорошо, неубедительно. Тогда давайте развернём углы наблюдений спинов частиц запутанной пары на 60 градусов относительно друг другу. Корреляция будет составлять ½, потому что в ¾ случаев спины будут совпадать, а в ¼ случаев будут противоположны. Среднее арифметическое от произведения спинов будет (+1)*¾ + (-1)*¼ = ½.
Если же вы повернёте свои раскрашенные шарики или детекторы на 60 градусов, и проведёте детектирование цветов точек в одном направлении, то вы получите другую статистику. У вас совпадение будет в 2/3 случаев, это сектор 60…180, противоположные цвета будут в ⅓ случаев, это сектор 0…60. У вас корреляция будет (+1)*2/3+(-1)*⅓=⅓.
У нас с вами разные результаты. Там, где корреляция равна ½ происходит явление квантовой запутанности, а там, где ⅓ — просто заранее определённые величины.
Слушатель:
— Ну да, с шариками я не смогу получить такую корреляцию с углами 60 градусов. Но я могу предложить другой опыт с 60 градусами, где получаются такая же корреляция ½.
Докладчик:
— Неужели?
Слушатель:
— Конечно. Это будут опыты со стаканчиками и шариками. Пусть у Алисы и у Боба по 8 непрозрачных стаканчиков. Стаканчики пронумерованы числами от 1 до 8. Все закрывают глаза. Ведущий подкладывает в стаканчики Алисы и Боба по одному шарику в стакан с одинаковым номером. После этого все стаканчики ставит вверх дном. Всё открывают глаза. Задача Алисы и Боба определить псевдоспин следующим образом. Сначала каждый из них выбирает по 4 стакана, которые будут открываться одновременно для проверки наличия шарика. Сделав выбор 4 стаканчиков из 8 Алиса и Боб таким образом выбирают направления детектирования своего псевдоспина. Выбранным стаканчикам присваиваются значения +1, остальным -1, образуется 8-мерный вектор. Например, [+1,+1,+1,+1,-1,-1,-1,-1] это вектор выбора Алисы направления детектирования псевдоспина. Если Алиса и Боб будут выбирать одинаковый вектор детектирования, то они всегда будут получать один и то же результат. А вот если выбранные вектора наблюдений будут различаться на 2 стакана, например
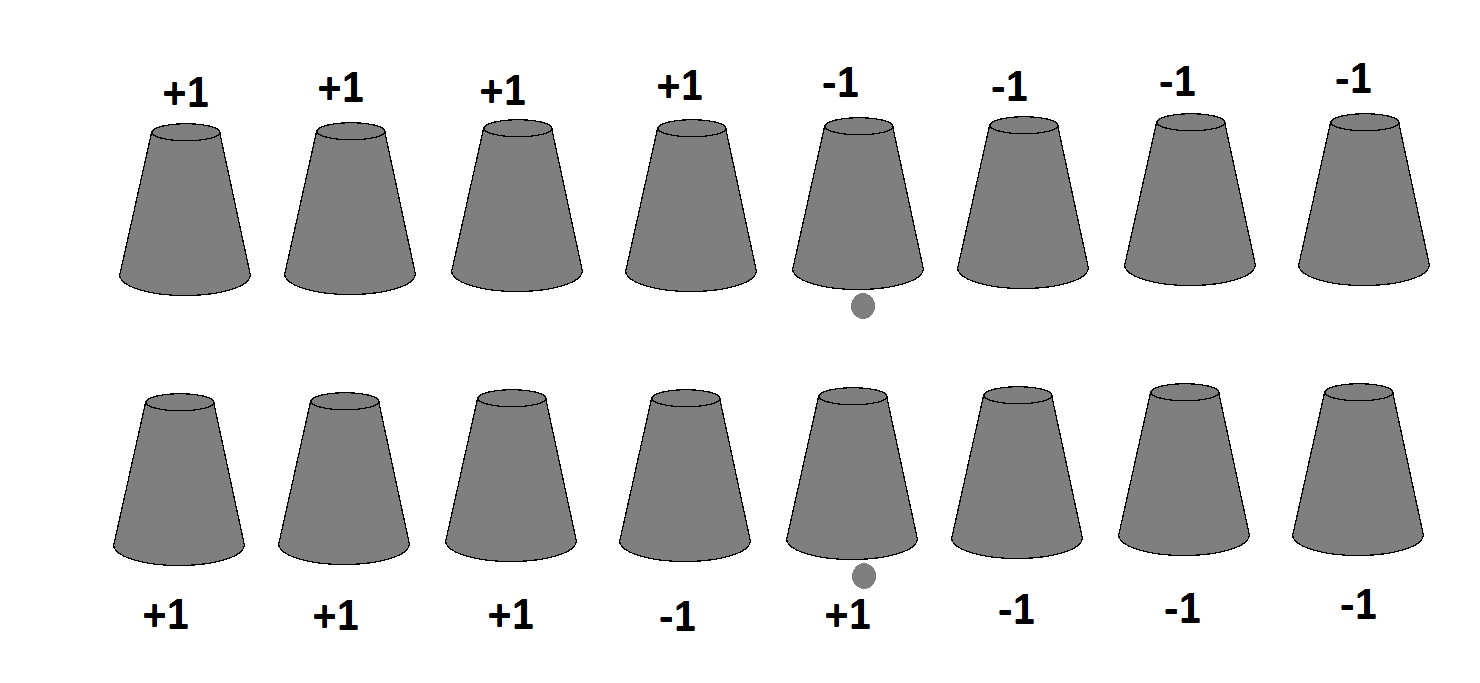
тогда совпадать результаты будут в 6 случаях из 8, и в 2 случая результаты будут противоположны. Корреляция будет (+1)*6/8 + (-1)*2/8=½.
Докладчик:
— Да, но почему вы решили, что углы между векторами выбора равны 60 градусов?
Слушатель:
— А очень просто. Скалярное произведение между векторами выборов нормированное на 8 равно (1+1+1+1–1–1+1+1+1)/8=4/8. Так как cos (60)=½ то угол между ними и есть 60 градусов. Получаем точно такой же результат, который вы приводите с измерением спина в направлениях 60 градусов. Это и есть квантовая запутанность?
Докладчик:
— Нет, конечно. У вас действительно тот же результат, но с заранее определёнными параметрами. А давайте тогда рассмотрим измерения не в двух фиксированных углах, а в трёх. Мы будем случайно выбирать одно из трёх заданных направлений измерения.
Слушатель:
— Да, только давайте возьмём те же 60 градусов, чтобы мне было легче строить аналогичный неквантовый эксперимент.
Докладчик:
— Хорошо. Если мы рассмотрим три направления детектирования спина, каждый с каждым относится как 60 градусов мы получим корреляции ½. AB=60, BC=60, AC=60.
Слушатель:
— Но я тоже могу составить вектора со взаимными углами 60 градусов. Вот они
A=[+1, +1, +1, +1, -1, -1, -1, -1]
B=[+1, +1, +1, -1, +1, -1, -1, -1]
C=[+1, +1, +1, -1, -1, +1, -1, -1]
Докладчик:
— Да, действительно, опять вы смогли получить то же самое без квантовой запутанности, корреляции естественно будут те же. Ну тогда может попробуем углы выбрать так AB=60, AC=60, BC=90.
Слушатель:
— Хорошо, вот вам те же углы AB=60, AC=60, BC=90.
A=[+1, +1, +1, +1, -1, -1, -1, -1]
B=[+1, +1, +1, -1, +1, -1, -1, -1]
C=[+1, +1, -1, +1, -1, +1, -1, -1]
Корреляция при измерении в направлениях В и С будут нулевые, так как в половине случаев шарик будет попадать в стаканчики с одинаковыми значениями (+1) либо (-1), в половине с разными значениями.
Докладчик:
— Да, пока что при всех выбранных углах доказать, что данная статистика является следствием квантовой запутанности не удаётся. Ну тогда давайте возьмём такие углы между направлениями измерений AB=60, BC=60, AC=120. Соответствующие корреляции будут ½, ½, -½.
Слушатель:
— Вот теперь я не могу на стаканчиках выбрать аналогичные углы. А если я выберу такие углы на шариках, то получу другие корреляции ⅓, ⅓, -⅓. Но я могу получить такие же корреляции на радиосигналах. Представьте, что есть две передающие антенны линейной поляризации. Они передают статистически независимые сигналы равной мощности. Одна передающая антенна ориентирована в горизонтальной поляризации, другая в вертикальной. На приёме имеются также две антенны линейной поляризации, они направленны на приём сигнала от передатчика, но ориентировать их поляризацию можно произвольно. Если их поляризацию ориентировать таким же образом A=120, B=60, C=0 то и корреляции принимаемых сигналов будут соответствующими
Corr
Corr
Corr
Значит ли это что принимаемые сигналы квантово-запутанные?
Докладчик:
— Нет. Тут принципиальное различие. Ваши принимаемые сигналы имеют произвольную амплитуду, они аналоговые. А в квантовом эксперименте сигналы квантованные, они принимают только два значения +1 и -1. Если бы вы получили те же корреляции, но сигнал был бы у вас квантованным, то вы бы тоже получили эффект квантовой запутанности.
Слушатель:
— Я действительно не могу получить такие корреляции на квантованном радиосигнале, и не могу опровергнуть ваш аргумент о том, что достичь такие корреляции можно только с помощью эффекта квантовой запутанности. Но отсутствие опровержения не есть доказательство. Может у меня просто не хватает фантазии придумать опровергающий эксперимент. Это ещё не значит, что у вас с такими корреляциями (½, -½, ½) происходит квантовая магия. В чем состоит признак квантовой запутанности?
Докладчик:
— Признак квантовой запутанности состоит в том, что представленные экспериментальные результаты корреляций невозможно описать в виде таблицы совместных вероятностей исходя из предположения о независимости двух событий. Первое событие, это наделение частицы определённым свойством по отношению к возможным измерительным воздействиям. Второе событие, это выбор измерительных экспериментов. Такая таблица совместных вероятностей представляет собой прямоугольную таблицу 8×9. Обозначим углы возможных измерений A=120, B=60, C=0. По вертикали таблица разделена на 8 строк это возможные свойства частицы, её реакцию на измерительное воздействие таких вариантов 8
A0B0C0 — при измерении в направлениях: A даст +1, B даст +1, С даст +1.
A0B0C1 — при измерении в направлениях: A даст +1, B даст +1, С даст -1.
A0B1C0 — при измерении в направлениях: A даст +1, B даст -1, С даст +1.
A0B1C1 — при измерении в направлениях: A даст +1, B даст -1, С даст -1.
A1B0C0 — при измерении в направлениях: A даст -1, B даст +1, С даст +1.
A1B0C1 — при измерении в направлениях: A даст -1, B даст +1, С даст -1.
A1B1C0 — при измерении в направлениях: A даст -1, B даст -1, С даст +1.
A1B1C1 — при измерении в направлениях: A даст -1, B даст -1, С даст -1.
По горизонтали такая таблица разделена на 9 столбцов, это 9 возможных вариантов проведения измерения AA, AB, AC, BA, BB, BC, CA, CB, CC. Пусть вероятность каждого варианта измерения будет равна 1/9. Если мы захотим построить такую таблицу совместных вероятностей, то в каждой ячейке будет вероятность события св-ва частицы, которая определяется строкой, при условии, что экспериментатор выбрал измерения в углах, которые соответствуют столбцу ячейки. Так как события независимы, то вероятность равна произведению вероятности строки на вероятность столбца. Осталось определить вероятность каждой из 8 строк и перемножить на 1/9. Для этого сформулируем несколько условий для вероятностей A0B0C0… A1B1C1 и решим систему в маткаде.

Получаем странный результат. Вероятности A0B1C0 и A1B0C1 отрицательные!
При найденных вероятностях строк, таблица совместных вероятностей выглядит так.

Глядя на эту таблицу вероятностей, можно увидеть нарушение неравенств Белла.
А теперь вторая часть. Хочу позволить себе немного пофантазировать и построить все же более реалистичную таблицу совместных вероятностей. Уж больно хочется ответить на вопрос –, а можно ли с помощью квантовой запутанности передавать информацию. Для этого я откажусь от требования независимости двух событий — выбор свойств пары квантовой частицы по отношению к измерениям и выбор экспериментатора углов измерения. Построить ячейки таблицы по результатам экспериментов не получится. Каждый эксперимент показывает только два угла, по которым производились измерения, но не показывает, как бы частица отреагировала, если бы её измеряли по третьему углу. Поэтому, попытаюсь построить таблицу методом подгонки.
Возьмём за основу наиболее близкую таблицу с неотрицательными значениями вероятностей. В эксперименте с шариками корреляции были ⅓, значит таблицу можно построить для этой корреляции с неотрицательными значениями.

Снова с помощью маткада находим решения. Как видим, все вероятности получаются неотрицательные. Таблица, составленная на основе данного распределения вероятностей по строкам выглядит так:

Следующим шагом я модифицирую столбики этой таблицы так, чтобы получить необходимые корреляционные соотношения.

Полученная таблица выполняет всем требованиям вероятностей и корреляционным соотношениям при углах A=120, B=60, C=0. Но ради неотрицательных вероятностей в таблице пришлось отказаться от выполнения требования независимости событий. В ней так же нарушается неравенство Белла P[A+B+] И все же интересно, можно ли повлиять на вероятность какого-нибудь результата измерения на одной точке путём проведения определённых измерений на другой точке? Например, если первая частица измеряется под углом A, то вероятность получить на второй частице результат С+ это сумма тех ячеек столбца P[AC], которые дают С+. P[C+]=2/144+0+3/144+3/144=8/144=1/18. Если первая частица измеряется под углом B, то вероятность получить на второй частице результат С+ это сумма тех ячеек столбца P[BC], которые дают С+. P[C+]=4/144+0+2/144+2/144=8/144=1/18 Вероятность получения результата измерений одной величины никак не зависит от того, как проводилось измерение на другой точке. Вывод: передача информации от одной квантовой частицы путём воздействия на другую невозможна.
