Что нам стоит дорогу построить. Часть 1
Ежедневный маршрут большинства из нас ограничивается поездкой из дома на работу и обратно. И самое сложное препятствие, которое может замедлить наше передвижение, — это пробки. Но в нашей стране есть огромное количество мест, куда можно добраться только на спецтранспорте.
Такой транспорт хорош, если не требуется возить большие объемы грузов или ездить в столь труднодоступные области на регулярной основе. Тогда нам уже стоит задуматься о строительстве инфраструктуры, передвижение по которой возможно и на привычном гражданском транспорте.
И хорошо, если вся сложность проектирования будущего маршрута заключается в поиске линейки и карандаша, чтобы начертить прямую линию на карте, соединяющую пару объектов. Но, увы, наша реальность сильно отличается от этого. Что делать, если местность при полете над ней напоминает хороший кусок швейцарского сыра?

Больше года мы с коллегами из научной лаборатории Digital Design работаем над созданием инструмента, который сможет строить различные сети коммуникаций в автоматическом режиме. За подробностями добро пожаловать под кат.
С чего все начиналось
Обычно поездки в подобные глухие места обусловлены определенной финансовой выгодой. И хоть зачастую заранее известно, что освоение данных районов принесет неплохую прибыль, почему бы не сэкономить средства на вещах, на которых это сделать можно без особых трудностей? Что если более грамотно спроектированная трасса позволит не строить несколько лишних километров автодороги?
Но только наличия автодорог для получения какой-то значимой прибыли явно недостаточно. И в основном ее приносят только залежи полезных ископаемых. Поэтому помимо автодорог необходимо проектировать сеть различных трубопроводов, сеть водоводов, сеть ЛЭП с правильно расставленными электрическими подстанциями. Всю эту инфраструктуру можно обозначить, как линейные объекты.

И когда инженер сталкивается с задачей проектирования сети коммуникаций на местности со сложными инженерно-геологическими условиями, на него ложится невероятно сложная аналитическая задача.
Как не попасть в зону разлива рек? Как минимизировать путь по многолетнемерзлым грунтам? Как сэкономить на объеме песчаной подушки при прокладке дороги по болоту? Где взять песок для этой подушки?
Это лишь малая толика вопросов, которые задает себе инженер во время работы, а ведь еще надо учесть различные ГОСТы и СНиПы. И ладно, если требуется соединить лишь два объекта, а если объектов пара десятков?
Поэтому сфера проектирования остро нуждается в инструменте, способном посчитать, как стоимость запроектированных инженером линейных объектов, так и обладать способностью строить их в автоматическом режиме.
Данные
Первое, с чем нам пришлось столкнуться, когда мы приступили к задаче — это поиск данных. Какие требуются данные? Где их взять? И если второй вопрос можно решить с помощью пользователя, то вот для понимания первого вопроса нам потребовалась серьезная аналитика.
А данных для корректного расчета требуется реально много — начиная от самой банальной разметки местности, на которой отмечены озера и реки, различные болота, а также и карстовые области, на которых крайне не рекомендуется строить из-за угрозы обрушения. Поэтому помимо областей, которые можно заметить со спутника, здесь также требуются данные геологического исследования местности.
Но не все данные ограничиваются у нас природными объектами. Есть также куча вещей, которые были созданы человеком. Например, в случае строительства дорог, мы можем использовать дороги, которые были построены ранее. А вот при строительстве трубопроводов использование существующей инфраструктуры далеко не всегда возможно. Так как подсоединение нового трубопровода к существующей сети вполне может не пройти гидравлический расчет.
Помимо переиспользования того, что было ранее создано человеком, нужно еще учитывать различные ограничения на строительство вблизи каких-либо объектов.Например, для строительства ЛЭП нужно учитывать отступы от мест человеческого обитания в зависимости от напряжения на самой ЛЭП.
Но не совсем корректно рассматривать расчет задачи только на плоскости, так как помимо ровной местности, есть участки с большим перепадом высот, на которых тоже нельзя вести строительство.
Получение данных по рельефу местности, гораздо более простой процесс, чем данных о разметке областей и существующей инфраструктуре. Для упрощения разработки мы пользуемся открытыми данными высот SRTM (Shuttle Radar Topography Mission), которые может получить любой желающий.

Итак, данные у нас есть, мы знаем, где мы можем строить, где не можем строить, имеются стоимости строительства для разных областей местности. У нас есть регион, на нем расположен набор объектов, которые мы хотим связать в единую коммуникационную сеть. В математических терминах это будет звучать как поиск решения задачи Штейнера.
Немного математики
Известно, что каждая формула уменьшает количество читателей вдвое, поэтому этот раздел мы драматически сократили…
Для того чтобы оптимизировать трассу проектируемого линейного объекта, требуется уметь вычислять его стоимость строительства. Каждый линейный объект можно представить в виде ломаной , состоящей из отрезков
.
Стоимость строительства каждого прямого отрезка можно представить в виде значения функции , где каждый отрезок задается параметрически:
$$display$${\displaystyle AB_i\colon \left\{ {\begin{aligned} &s=s\left (t\right) — \mbox{параметризованная кривая}, \\ &h=h\left (s (t)\right) — \mbox{функция высоты рельефа},\\ &c=c\left (s (t)\right) — \mbox{функция удельной стоимости строительства в точке},\\ \end{aligned}}\right.}$$display$$
где — отрезок параметризации.
, где
— метрический тензор поверхности Земли без учета рельефа, то есть, простыми словами, функция измерения расстояния на поверхности Земли.
Из-за того что наша планета имеет форму геоида, то для измерения расстояний приходится пользоваться особыми формулами. Для этого мы используем формулу Гаверсинусов. В ней форма планеты имеет вид сферы, но этого для наших целей достаточно, так как погрешность измерения составляет около 0.3%, а скорость вычисления расстояний данным способом остается высокой.
Подходы к поиску оптимального пути

Но прежде чем переходить к соединению группы объектов, нужно научиться находить оптимальный путь между двумя. На ум сразу же приходит два способа, как это сделать:
- построить граф, а дальше применять методы поиска кратчайшего пути;
- использовать решение, основанное на методах оптимизации.
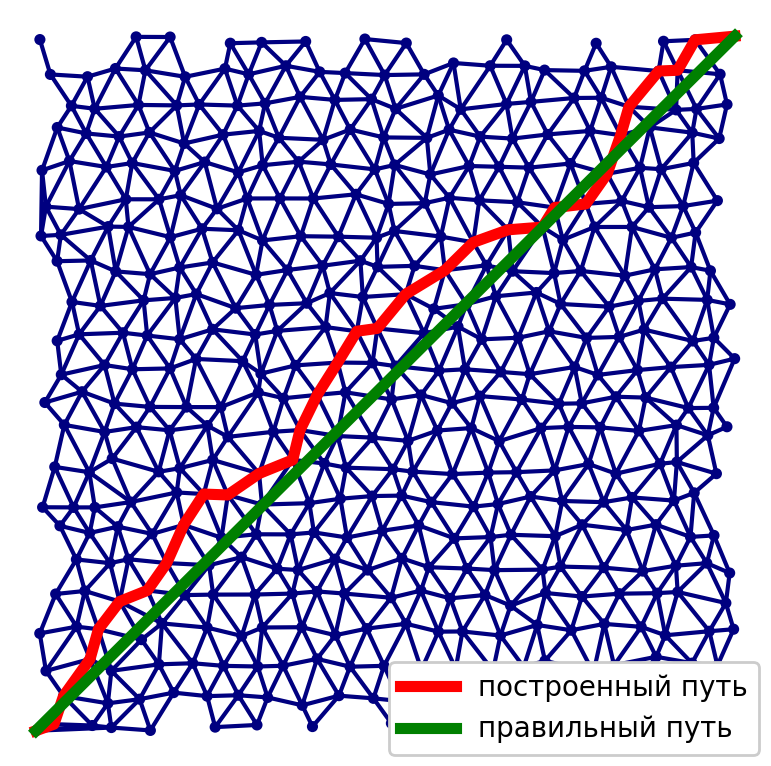
При реализации первого способа у нас возникает проблема, связанная со способом построения графа для получения как можно более высокой точности решения. Необходимо найти баланс между количеством вершин и ребер в графе, качеством решения и временем, затраченным на его вычисление.
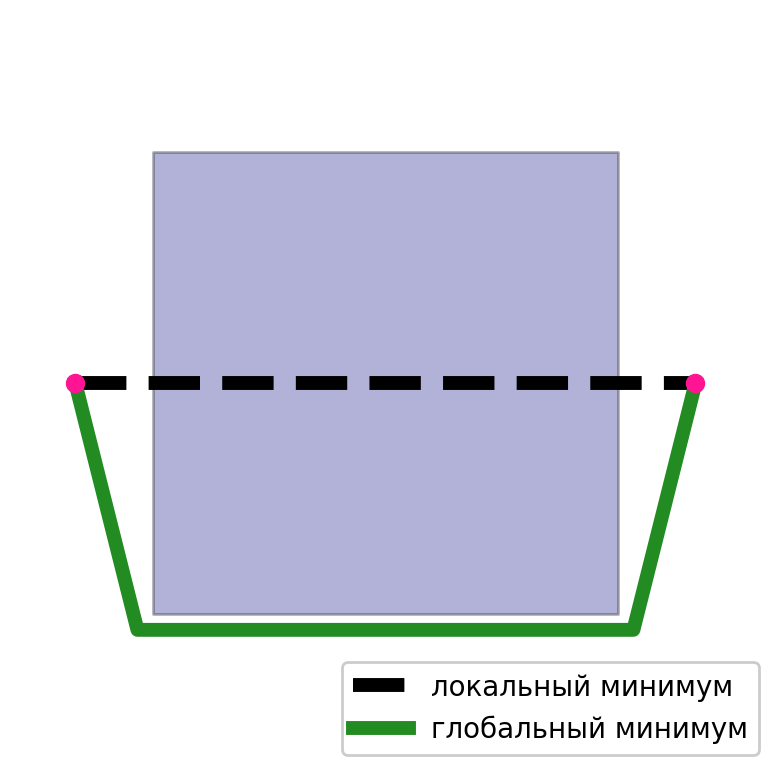
Во втором случае главная проблема — это локальные минимумы. Легко подобрать случай, когда решение может не сойтись или быть далеким от оптимального. Так как решение, получаемое данным способом, невероятно сильно зависит от начального приближения. Если у нас есть хорошее начальное приближение, то и результат будет качественный.
Итак, у нас есть два подхода к решению данной задачи. У первого достаточно низкое качество, но нет проблемы локальных минимумов. У второго есть проблема локальных минимумов, но зато высокое качество решения. И если корректно соединить эти два подхода, то недостатки каждого исчезнут. Решение, полученное на графе, берем в качестве начального приближения, а после применяем к нему методы оптимизации.
В этой части статьи мы рассмотрим именно предлагаемое решение данной задачи на графе.
Выбор инструментария
План действий намечен, осталось лишь это «закодить». Так как на начальном этапе написания приложения у нас было мало знаний о предметной области, то нам был нужен гибкий язык, чтобы в случае каких-то грубых архитектурных просчетов переписать весь код за пару банок пива вечеров. Также опционально хотелось наличия библиотек на все случаи жизни, чтобы не прибегать к изобретению велосипедов. Поэтому в качестве основного языка программирования был выбран Python.
В приложении мы использовали внушительный технологический стек, который не ограничивается нижеприведенным:
- shapely для работы с геометрическими данными, такими как многоугольники и ломаные линии;
- geopandas для удобной работы с shapely;
- scipy для хранения расчетного графа и поиска кратчайшего пути на нем, а также поиска минимальных остовных деревьев;
- PyTorch для работы со стоимостной функцией;
- pillow для работы с изображениями.
Реализация
В работе модуля можно выделить несколько этапов:
- генерация стоимостной функции;
- генерация вычислительной сетки;
- построение графа на основе сетки;
- взвешивание графа;
- вычисление кратчайших путей на графе.
Так как ребра графа представляют собой отрезки, то взвешивать эти ребра мы можем с помощью вычисления значения определенного интеграла, который представлен выше. Но ребер в графе очень много, а, соответственно, значения стоимостей и высот потребуется получить для очень большого количества точек, что может занимать много времени.
Изначально была идея находить удельную стоимость строительства путем определения принадлежности точки многоугольнику. Но эта мысль была отметена из-за высокой алгоритмической сложности данного подхода, так как многоугольников может быть много, и у каждого из них есть большое количество вершин.
Поэтому для решения этой проблемы, все многоугольники, которые у нас есть мы можем представить в виде картинки, что в математическом виде является матрицей. Таким образом, мы можем получать удельную стоимость строительства в точке за О (1), а значит и получать стоимость строительства определенного ребра с высокой точностью.
Теперь мы готовы построить граф, но не существует однозначно правильного способа его построения для получения решений высокой точности. Для того чтобы построить граф, требуется сгенерировать вычислительную сетку, а именно набор точек в рассматриваемой области, соединенных в соответствующем порядке отрезками, образующими грани ячеек. Сетки можно разделить на два вида: равномерные и неравномерные.


Модель равномерной сетки описывает координаты отдельных точек, таким образом что расстояние между узлами сетки одинаковое. Неравномерной сетка представляется в виде хаотичного набора отдельных точек.
Использование равномерной сетки не всегда будет давать качественный результат для поиска кратчайшего пути, поэтому необходимо опробовать данный подход на неравномерной сетке. Наиболее универсальной является треугольная сетка.
Сетка генерировалась путем внесения шума с определенным коэффициентом в равномерную прямоугольную сетку, а далее применения для этого набора точек триангуляции Делоне.
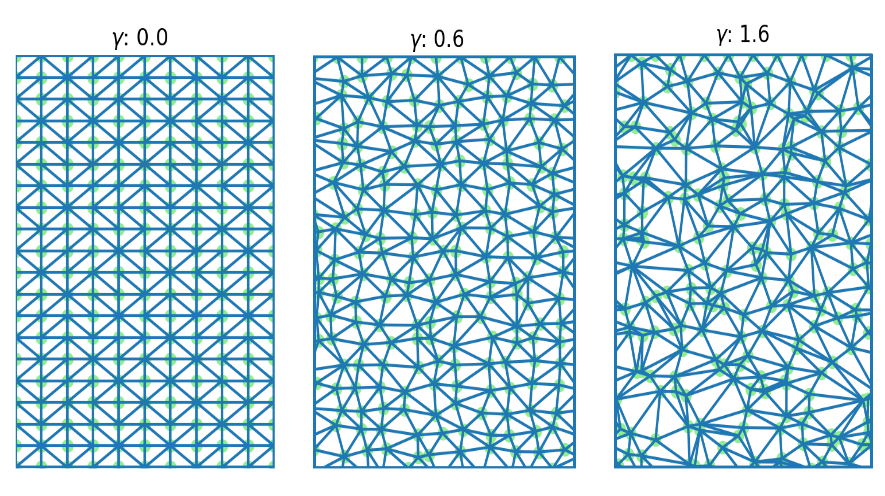
Эффективность построенных сеток проверялась на различных модельных картах местности, в которых учитывались различные стоимости областей и рельеф, а дальше проводилось сравнение с решением, полученным аналитически. Путем перебора длины ребра графа и коэффициента внесения шума в равномерную сетку были найдены оптимальные параметры для построения оптимального пути между двумя точками.
Основные проблемы
Сначала все шло хорошо, алгоритм рассчитывал оптимальные сети, но однажды возникла проблема с качеством построенного пути. Кейс был достаточно простой: нужно было соединить два объекта на достаточно протяженной карте. Алгоритм совсем не хотел строить маршрут, который был очевидно корректным.
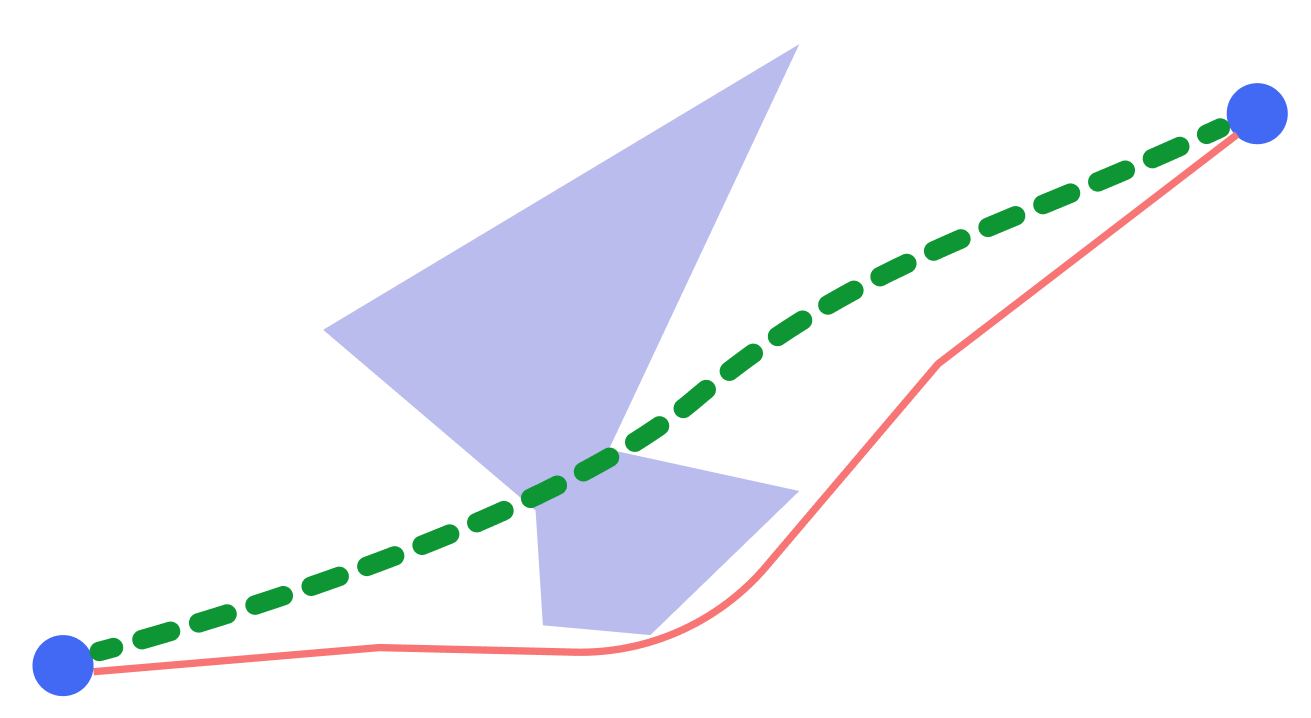
Проблема, как всегда, была с вычислительной сеткой. Мы продолжили наши эксперименты с внешним видом сеток и пришли к выводу, что соединение вершин в граф, где каждая вершина соединена с n-ближайшими соседями, является решением наших проблем.
Построение сетей
После того как мы научились находить оптимальные пути между двумя точками, следующим шагом мы взялись решить задачу построения оптимальной сети линейных объектов. Встречаемые в литературе алгоритмы построения деревьев Штейнера на графах ориентированы на более общие задачи, поэтому будут неэффективны в нашем случае. У нас граф является сильно разреженным, с малым числом терминальных вершин, относительно общего количества вершин в графе, а еще наша задача прикладная. Поэтому и по ряду других причин было решено разработать собственный алгоритм, использующий определенную эвристику для эффективного построения оптимальной сети.
Описание алгоритма построения оптимальной сети на графе для нашего случая — это тема для отдельной публикации, здесь мы его рассматривать не будем. Поскольку при расчете реальной задачи нужно учитывать множество дополнительных условий из строительной сферы, актуальных для конечного пользователя, которые и накладывают определенные ограничения на используемый алгоритм.
Реальный случай
Итак, теперь перейдем к результатам работы алгоритма. Нашей задачей является соединение заданного набора объектов коммуникационной сетью. Сравнение результатов работы алгоритма происходило с ранее построенной дорожной сетью. Общая протяженность существующей сети составляет 153.5 км против 122.6 км у рассчитанной. Это дает около 25% сокращения длины дорожной сети, что в итоге позволит сэкономить около 5–15% на затратах капитального строительства.
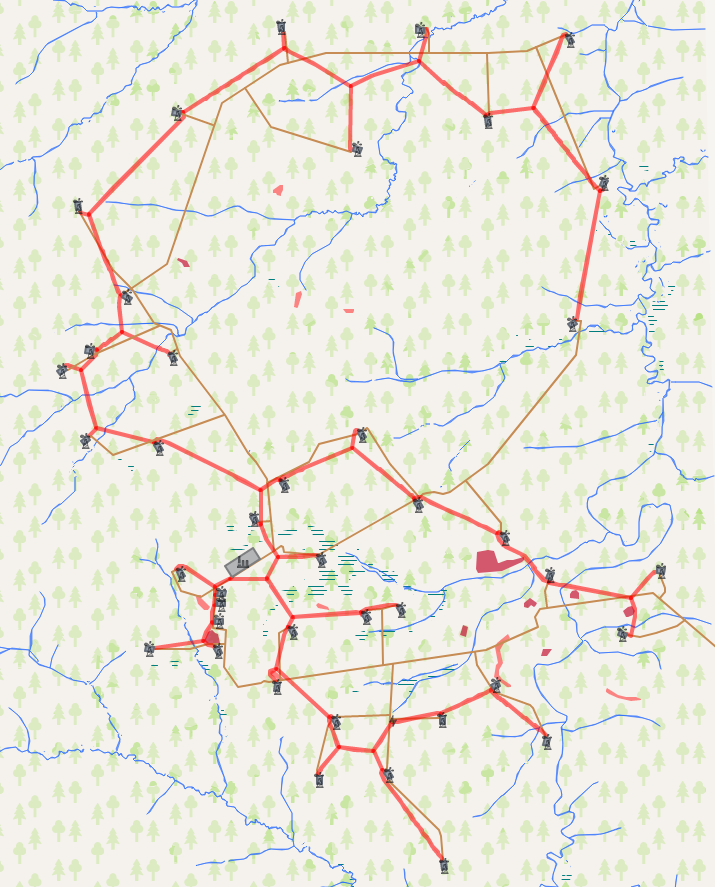
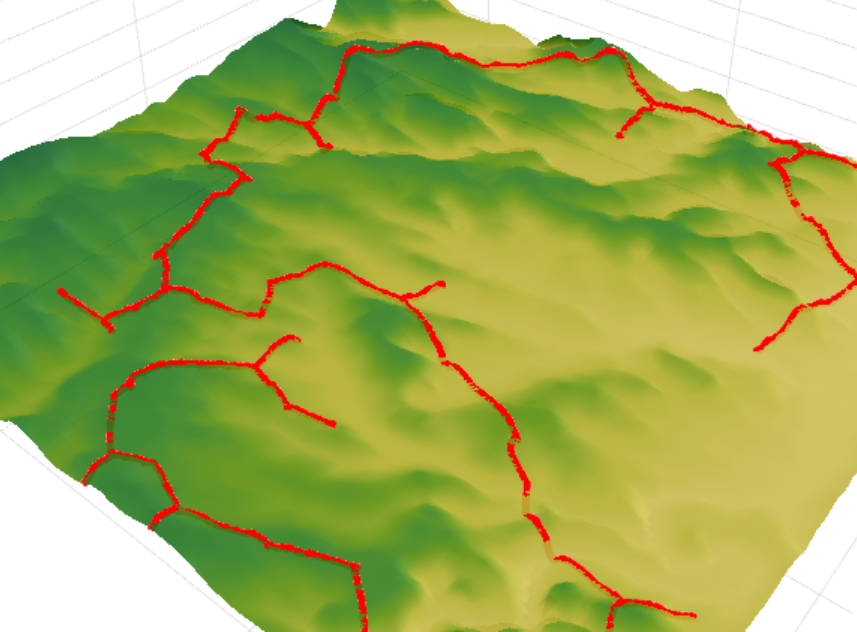
Внимательнее посмотреть результаты расчета можно здесь.
Описание применяемых методов оптимизации будет в следующей части статьи.
