Численный анализ эффективной площади рассеяния в двумерной осесимметричной постановке
Чтобы избежать обнаружения радарами противника, современные истребители, корабли и ракеты должны иметь наименьшую эффективную площадь рассеяния (ЭПР). Учёные и инженеры, разрабатывающие такие малозаметные объекты, с помощью методик вычислительной электродинамики оптимизируют ЭПР и эффекты рассеяния произвольных объектов при использовании радаров. Рассматриваемый объект рассеивает падающие на него электромагнитные волны во всех направлениях, и часть энергии, возвращаемая к источнику электромагнитных волн в процессе т.н. обратного рассеяния, формирует своеобразное «эхо» объекта. ЭПР как раз является мерой интенсивности радиолокационного эхо-сигнала.
На практике применяют эталонную проводящую сферу в качестве объекта для калибровки радаров. Аналогичная постановка проблемы используется для верификации численного расчета ЭПР, поскольку решение данной классической задачи электродинамики было получено Густавом Ми еще в 1908 году.
В данной заметке мы расскажем о проведении такого эталонного расчета с помощью эффективной двумерной осесимметричной постановки, а также кратко отметим общие принципы решения широкого класса задач рассеяния в COMSOL Multiphysics®.
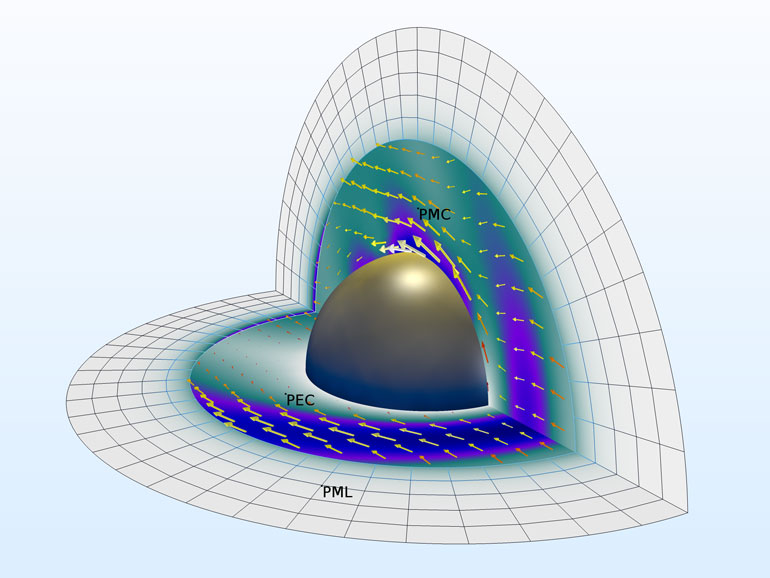
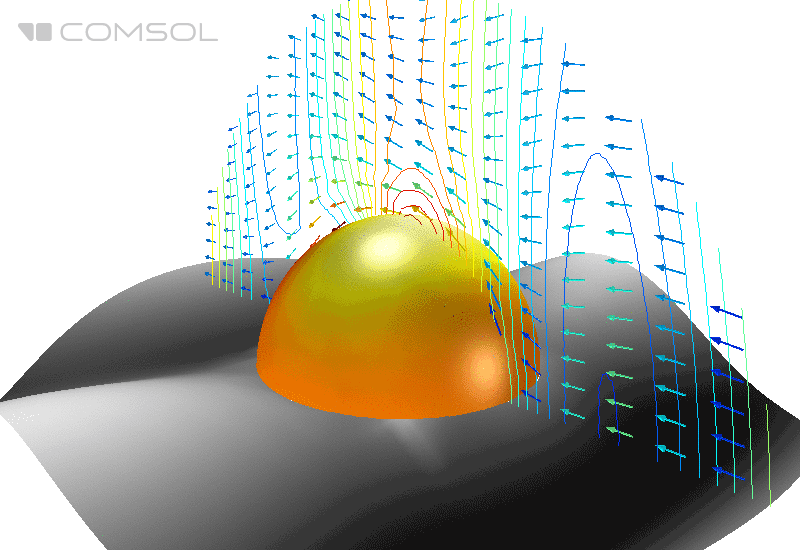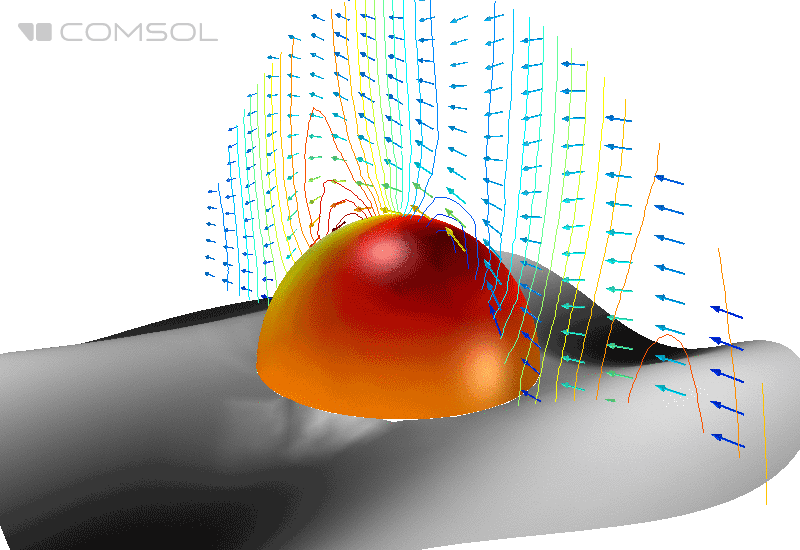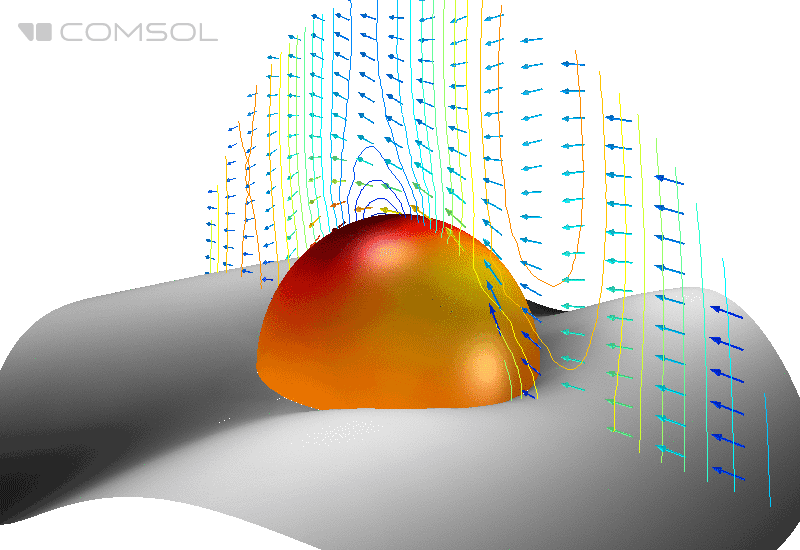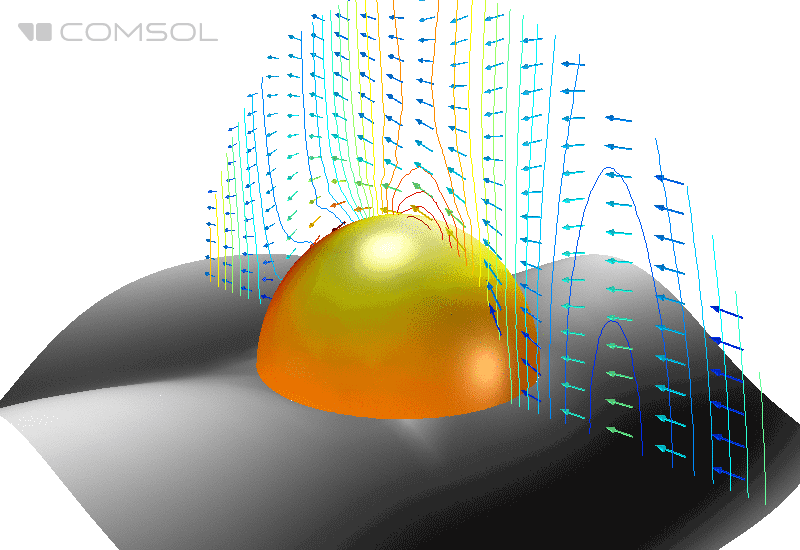
Рис. 1. Распределение электрического поля (его нормы) и усредненного по времени потока энергии (стрелки) вокруг идеально проводящей сферы в свободном пространстве.
В классическом эталонном примере, идеально проводящую металлическую сферу в свободном пространстве облучают плоской электромагнитной волной и вычисляют ЭПР.
На выходе обычно рассчитывают рассеяние в для различных соотношений радиуса сферы и длины волны, на основе которых выделяют три области: Рэлеевскую, оптическую и переходной Ми-диапазон.
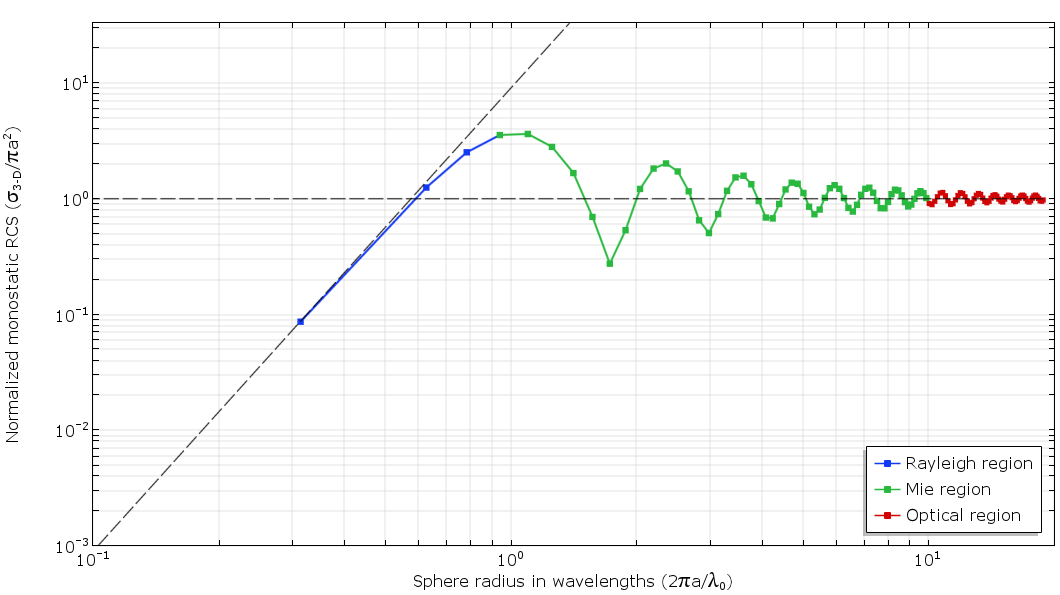
Рис. 2. График зависимости ЭПР от длины волны (в двойном логарифмическом масштабе). Выделены три характерные области: Рэлеевская, Ми и оптическая. Черными пунктирными линиями показаны асимптотические решения для Рэлеевской и оптической зоны.
На характеристики ЭПР оказывают значительное влияние электрический размер и материальные свойства объекта, на который падает луч радара. Поскольку электрический размер объекта — в нашем случае сферы — уменьшается при переходе из оптического диапазона в рэлеевскую область (через Ми-диапазон), асимптотические методы не обеспечат достаточной точности, чтобы учесть вклад всех физических явлений. Для получения точных результатов задачу следует решать с помощью полноволновых техник.
В трехмерной постановке даже с учетом использования идеально согласованных слоев (Perfectly Matched Layers — PML), позволяющих эффективно ограничить расчетную область и имитировать открытые границы, и условий симметрии, расчет с подробным разрешением по частоте/длине волны может занять достаточно много времени.
Подробнее тут.
К счастью, если объект является осесимметричным и рассеивает волны изотропно, проведение полного 3d-анализа не требуется. Чтобы проанализировать распространение электромагнитных волн и резонансное поведение объекта, достаточно провести расчет для его поперечного сечения в двумерной осесимметричной постановке при задании определенных условий.
Предположим, что наша сфера металлическая и имеет высокую проводимость. Для данной задачи поверхность сферы задается как идеальный электрический проводник (Perfect electric conductor — PEC), а её внутренняя часть исключается из расчетной области. Область вокруг нее определяется как вакуум с соответствующими материальными свойствами, а в самом внешнем слое используется PML сферического типа, используемый для поглощения всех исходящих волн и предотвращения отражения от границ расчетной области.
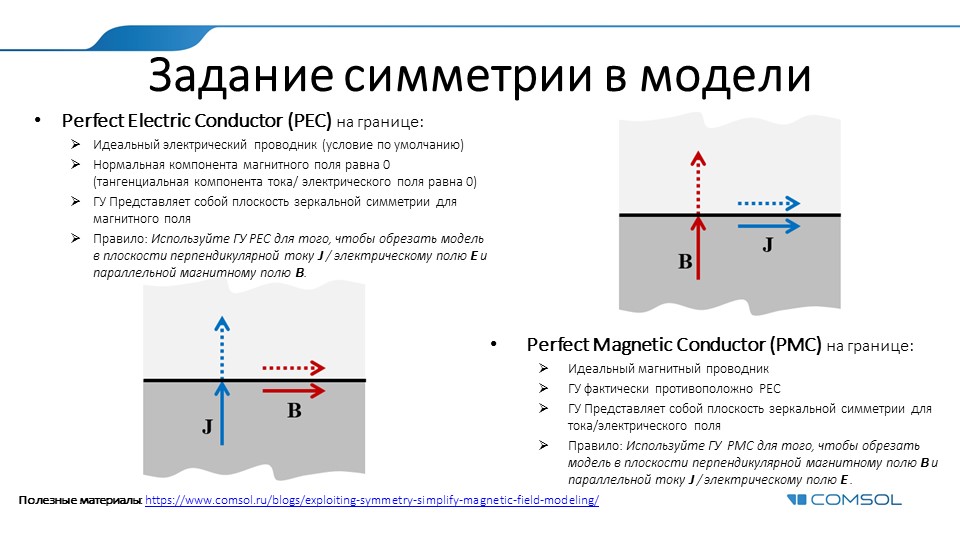
Для численного решения задач электродинамики в частотной области существует несколько приемов для эффективного моделирования металлических объектов. На иллюстрации ниже отражены техники и рекомендации по использованию Переходного граничного условия (Transition boundary condition — TBC), Импедансного граничного условия (Impedance boundary condition — IBC) и условия типа Идеальный Электрический Проводник (Perfect Electric Conductor — PEC).
Подробный разбор аспектов применения каждого из них тут.

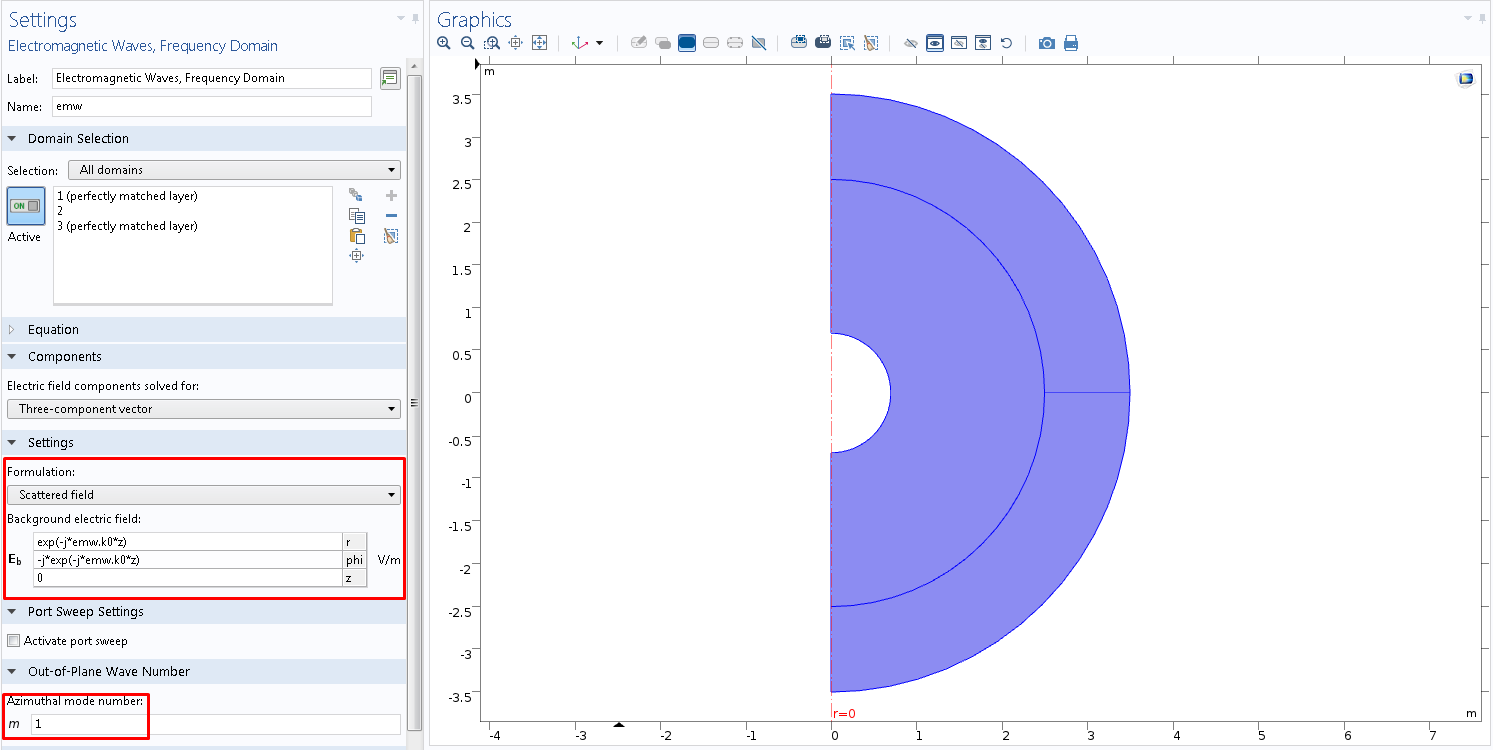
Рис. 3. Геометрия для осесимметричной постановки и задание фонового электромагнитного поля с левой круговой поляризацией в графическом интерфейсе COMSOL Multiphysics®.
В расчётной области (кроме PML) задается возбуждение фонового поля с левой круговой поляризацией, направленного в отрицательном направлении оси z (Рис. 3). Обратите внимание, что выставлен расчет только для первой азимутальной моды.
По умолчанию для СВЧ-задач в COMSOL Multiphysics® автоматически строится свободная треугольная (или тетраэдральная для 3D-задач) сетка под указанную для исследования в частотной области (Frequency Domain study) максимальную частоту, которая в рассматриваемом примере составляет 200 МГц. Чтобы обеспечить достаточное разрешение волновых процессов в модели, устанавливается максимальный размер элемента сетки, равный 0.2 длины волны. Другими словами пространственное разрешение задается как пять элементов второго порядка на длину волны. В идеально согласованных слоях сетка строится протяжкой в направлении поглощения, что обеспечивает максимальную эффективность работы PML.
Т.к. число степеней свободы в модели очень мало (по сравнению с трехмерной постановкой), то ее расчет занимает всего несколько секунд. На выходе пользователь может получить и визуализировать распределение электрического поля вокруг сферы (в ближней зоне), которое представляет собой сумму фонового и рассеянного полей.
Для данной задачи наиболее интересные характеристики относятся к области дальнего поля. Чтобы их получить в модели нужно активировать на внешней границе расчетной области (в данном случае на внутренней границе PML) условие Far-Field Calculation, что позволяет рассчитывать поля в дальней зоне за пределами расчетной области в любой точке на основе интегральных соотношений Страттона-Чу. Активация добавляет дополнительную переменную — амплитуду поля в дальней зоне, на основе которой в постобработке ПО рассчитывает инженерные переменные, соответствующие стандартам IEEE: эффективную изотропно излучаемую мощность, коэффициент усиления (т.н. Gain, в т.ч. учетом входного рассогласования), коэффициент направленного действия и ЭПР.
По полярному графику специалист может определить направленность поля в дальней зоне в определенной плоскости, а трехмерная диаграмма направленности в дальней зоне позволяет более подробно изучить поле рассеяния (рис. 4).
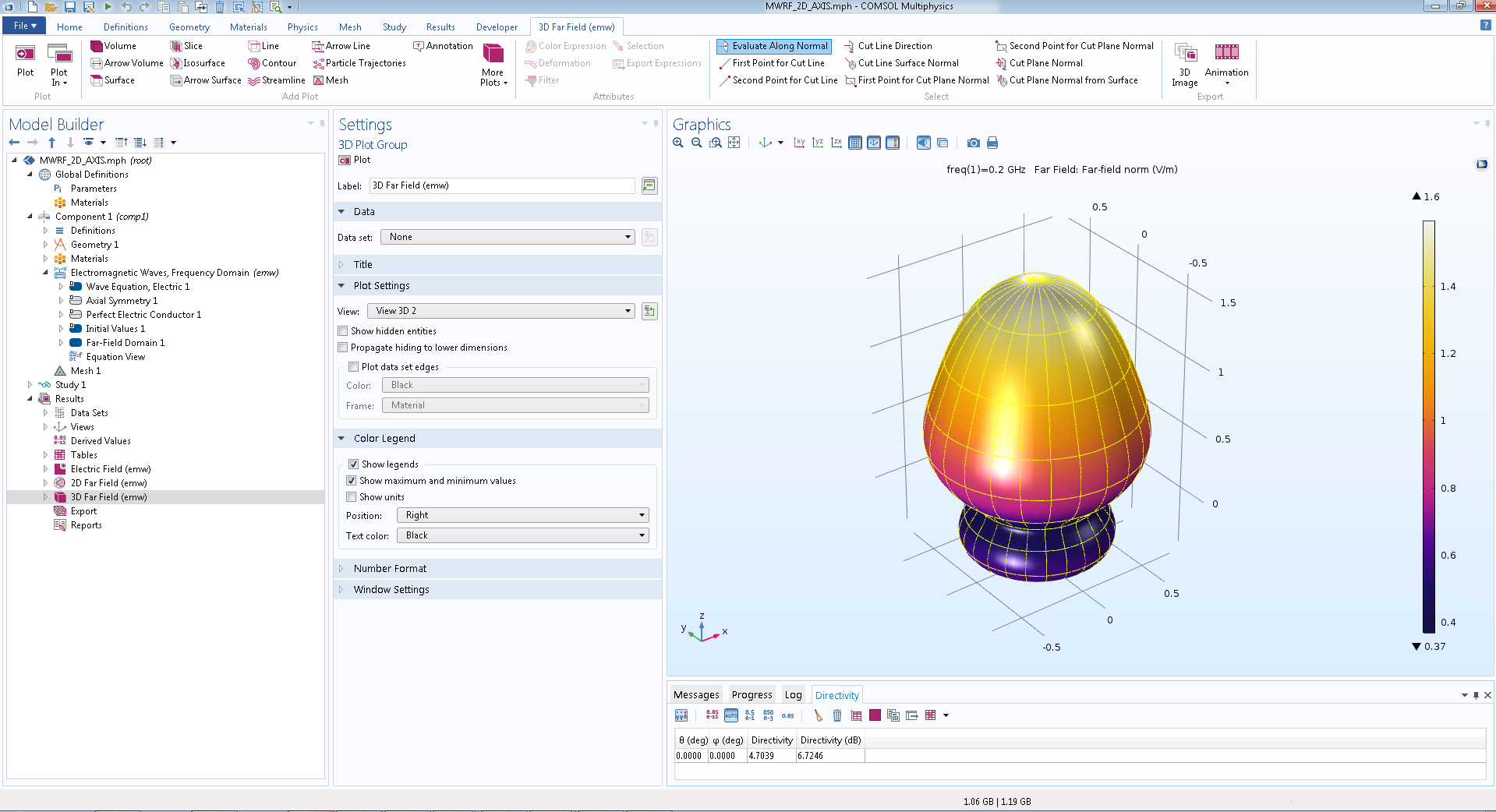
Рис. 4. Трехмерная визуализация поля в дальней зоне на основе двухмерной осесимметричной модели в COMSOL Multiphysics®.
Результаты для «сокращенной» модели в осесимметричной постановке относятся к процессу облучения проводящей сферы фоновым полем с круговой поляризацией. В исходной же 3d-задаче характеристики поля рассеяния исследуются для случая линейно-поляризованной плоской волны. Как обойти данное различие?
По определению линейную поляризацию можно получить, сложив правую и левую круговую поляризацию. Двухмерная осесимметричная модель с указанными выше настройками (Рис. 2) соответствует первой азимутальной моде (m = 1) фонового поля с левой круговой поляризацией. Решение для отрицательной азимутальной моды с правой круговой поляризацией легко вывести из уже решенной задачи, воспользовавшись свойствами симметрии и проведя простые алгебраические преобразования.
Проведя всего один двухмерный анализ и зеркально отобразив результаты уже в процессе постобработки, можно извлечь все необходимые данные, значительно сэкономив при этом вычислительные ресурсы (Рис. 5).
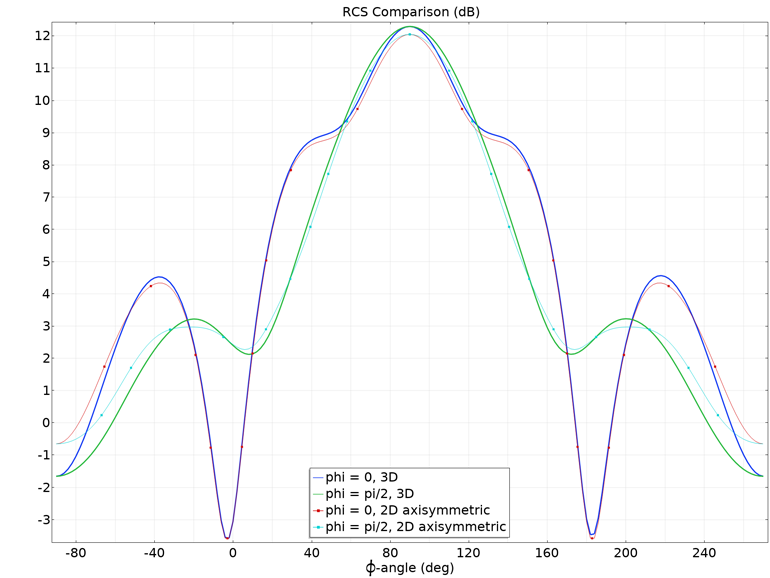
Рис. 5. Сравнение развертки эффективной площади рассеяния (в логарифмическом масштабе) по углам рассеяния для полного трехмерного расчета и предложенной двухмерной осесимметричной модели.
Одномерный график (Рис. 5) со сравнением ЭПР демонстрирует приемлемое соответствие между трехмерной и двухмерной осесимметричной моделями. Небольшое расхождение наблюдается лишь в области прямого и обратного рассеяния, вблизи оси вращения.
В дополнение для наглядной визуализации полученных двухмерных результатов в трехмерном пространстве потребуется преобразование системы координат из цилиндрической в декартову. На рис. 6 приведена трехмерная визуализация результатов для двухмерной осесимметричной модели.
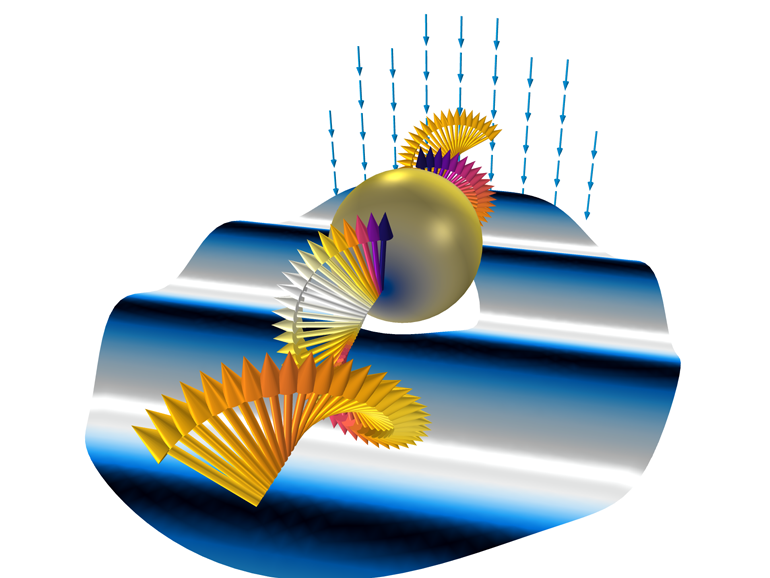
Рис. 6. Трехмерное представление полученных результатов на основе двумерного расчета.
Вращающиеся по спирали стрелки обозначают фоновое поле с круговой поляризацией. График в горизонтальном сечении представляет собой распределение радиальной составляющей фонового поля (волновой процесс отображен с помощью деформаций плоскости). На поверхности сферы построена норма полного электрического поля. Еще одна стрелочная диаграмма показывает суперпозицию двух круговых поляризаций, что эквивалентно фоновому полю с линейной поляризацией в трехмерном пространстве.
В процессе современной разработки в области радиофизики и микроволновой техники для инженеров эффективные приемы моделирования, сокращающие ресурсоемкость и затраты времени, незаменимы вне зависимости от применяемого метода численного анализа.
Для сохранения целостности и воссоздании всех релевантных физических эффектов при моделировании реального компонента, обладающего большим электрическим размером, возможно упростить процесс численного расчета без потери точности путем решения задачи в двухмерной осесимметричной постановке. При моделировании и анализе таких осесимметричных объектов, как рассеивающие сферы и диски, конические рупорные и параболические антенны, вычисления для сечения устройства выполняются на несколько порядков быстрее, чем при использовании полной трехмерной модели.
Короткий видеообзор (на рус.), в котором демонстрируются примеры моделирования СВЧ-антенн с помощью модуля Радиочастоты, включая расчет частотных характеристик S-параметров и импеданса, диаграммы Смита, исследование согласования, расчет полей в дальней зоне, определение коэффициента направленного действия (Directivity) и коэффициента усиления (Gain). Кроме того, рассмотрены принципы использования симметрии, моделирования антенн в режиме приёма и комплексных расчетов систем разнесенных в пространстве приемников и передатчиков, оценки электромагнитных наводок на соседние антенны и многое другое.

При этом простая двумерная постановка позволяет быстро восстанавливать в трехмерном пространстве и исследовать рассеяние фонового поля с линейной поляризацией, а также направленность излучения в дальней зоне для антенн, возбуждаемых электрической поперечной модой TE11 круглого волновода.
Данный материал основан на статье J.Munn. Fast Numerical Analysis of Scattering and Radar Cross Section, журнал Microwaves & RF от 3 мая 2018 г.
Функционал COMSOL Multiphsycics® позволяет также моделировать:
Для более подробного знакомства с возможностями нашего пакета для рассматриваемых в данной статье применений приглашаем поучаствовать в нашем новом вебинаре «Решение задач рассеяния в COMSOL Multiphsycics®», который состоится 22 августа 2018 года.
Бесплатная регистрация: http://comsol.ru/c/7eb9
Рассеяние волн — одно из наиболее фундаментальных явлений физики, т.к. именно в форме рассеянных электромагнитных или акустических волн мы получаем огромную долю информации об окружающем мире. Полноволновые формулировки, доступные в модулях Радиочастоты и Волновая Оптика, а также в модуле Акустика, позволяют детально моделировать эти явления с помощью метода конечных элементов. В данном вебинаре мы обсудим сложившиеся практики решения задач рассеяния в COMSOL, включая использование формулировок рассеянного поля (Background Field), функционала по анализу полей в дальней зоне (Far-Field Calculation), проведения широполосных расчетов с помощью новых технологий на основе разрывного метода Галеркина (dG-FEM), а также моделирования антенн и датчиков в режиме приема сигнала.
В завершение вебинара мы обсудим доступные шаблоны и примеры в Библиотеке моделей и приложений от COMSOL, а также ответим на вопросы пользователе по данной теме.
Также можно запросить демонстрационную версию COMSOL в комментариях или на нашем сайте.
Финальная гифка: