Численное моделирование – история одного проекта

Привет, Хабр и его уважаемые читатели!
В статье (ссылка) мы рассказали о нашем опыте внедрения инструментов численного моделирования в исследовательскую практику металлургической компании. Рады, что тема нашла поддержку и вызвала интерес у читателей ресурса. Сегодня мы расскажем о практической стороне вопроса применения численных методов для решения прикладных задач, а именно о ходе реализации одного из наших проектов. Речь пойдет о промышленной шредерной установке, предназначенной для измельчения металлолома и его очистки от примесей.
Сырьем для шредера является металлолом, а результатом работы — металлический шрот. Измельчение металлолома позволяет повысить его насыпную плотность, а главное провести сортировку и удалить примеси, в том числе цветные металлы, которые тоже идут в переработку, но отдельно.
Объектом нашего исследования стала опорная рама виброжелоба, транспортирующего шрот из измельчителя на конвейерную ленту. Для того, чтобы шрот не задерживался в виброжелобе, сам желоб подвергается динамическим нагрузкам — вибрирует.
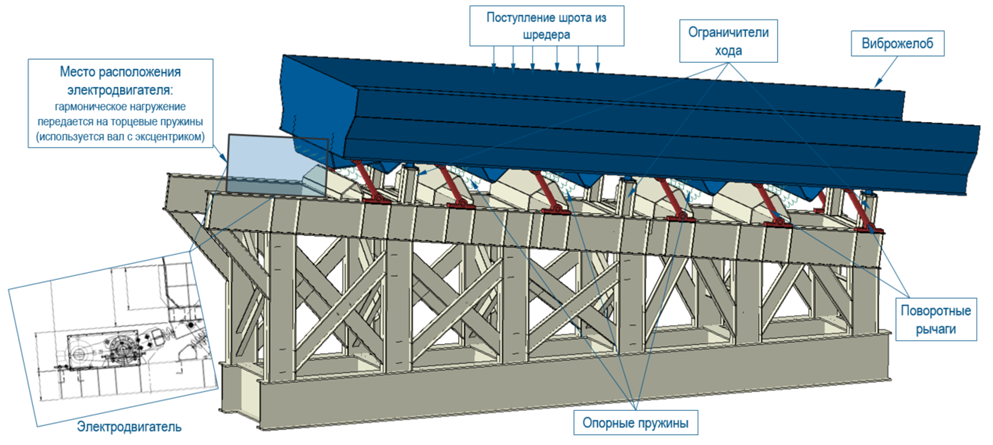
Геометрическая модель виброжелоба и опорной рамы
Во время обслуживания оборудования стали выявляться трещины на опорной раме, в основном — по сварным швам. Причина образования повреждений не могла быть установлена обычными методами в основном потому, что во время работы шредера доступ персонала к нему запрещен. Необходимо было разработать и внедрить мероприятия, направленные на устранение причин образования трещин и повышение надежности оборудования. Цель нашего участия — методами численного моделирования проверить сформулированные заказчиком гипотезы по механизму разрушения опорной рамы и возможным корректирующим действиям.
Самым проблемным этапом работы стал сбор исходных данных. В теории, в качестве исходных данных расчетчику предоставляются геометрия объекта (чертежи или готовые геометрические модели), данные по механическим характеристикам материалов и условиям нагружения. Точность исходных данных напрямую влияет на достоверность результатов расчетной модели. В нашем проекте значительного количества данных не было, и эти пробелы заполнялись «ручными» измерениями.
В результате была собрана геометрическая модель шредера, построена конечно-элементная модель, расставлены все условия крепления и начаты расчеты.
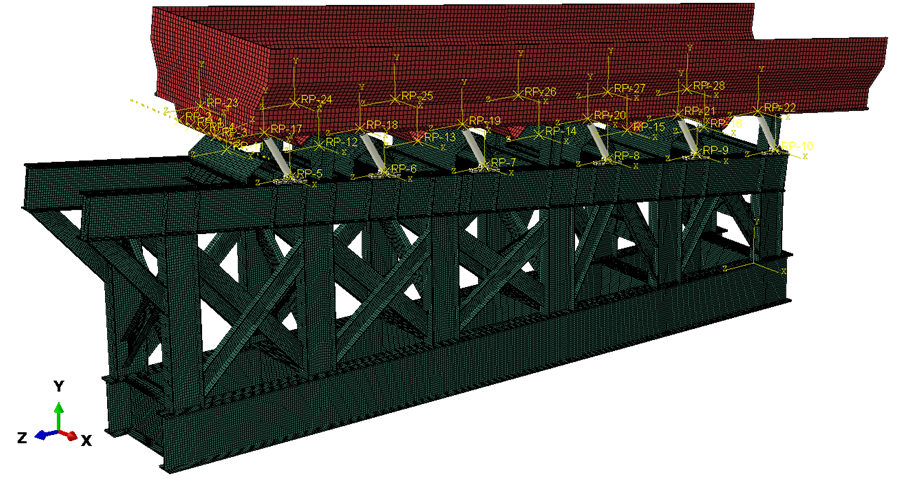
Конечно-элементная модель: Листовые элементы металлоконструкций аппроксимировались оболочечными конечными элементами (КЭ); узлы крепления поворотных рычагов — твердотельными КЭ; поворотные рычаги — балочными КЭ
Начали с оценки статической прочности конструкции. Внешние нагрузки: собственный вес конструкции и масса шрота при различном уровне заполнения виброжелоба. Статический анализ показал, что даже при полной загрузке желоба шротом, уровень механических напряжений существенно ниже предельных значений и не может быть причиной разрушения металлоконструкции.
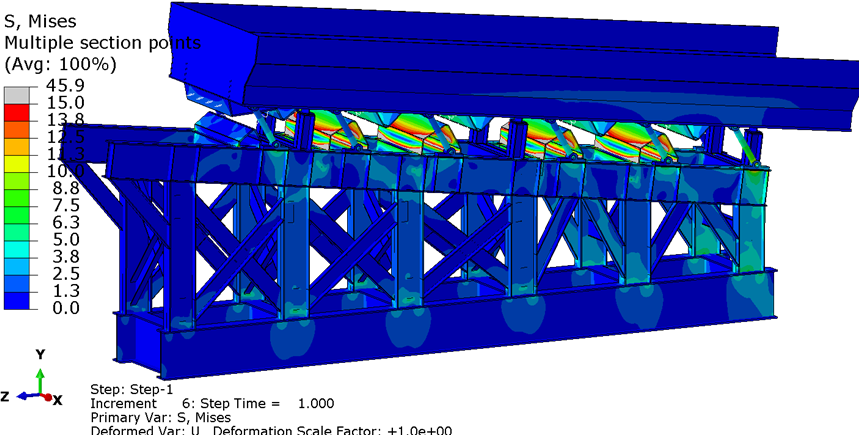
Статический анализ: распределение эквивалентных напряжений по Мизесу при полной загрузке желоба шротом, МПа
Частотный анализ конструкции показал, что частота внешней гармонической нагрузки близка к частоте колебаний по 3-й собственной форме, что может стать причиной резонанса.
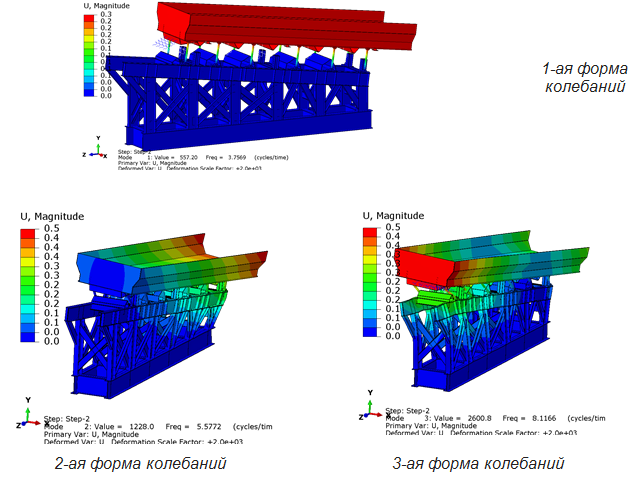
Что произойдет с конструкцией опорной рамы при возникновении резонансных колебаний?
Для ответа на этот вопрос была проведена серия линейных (модальная динамика) и нелинейных динамических расчетов, в которых мы намеренно пытались ввести систему в резонанс. Варьировались следующие параметры: частота внешней нагрузки ±15% от базового значения, уровень наполнения «кузова» желоба шротом (влияет на динамические характеристики системы) и жесткость пружин ±15% от базового значения. Были получены значения варьируемых параметров и их комбинаций, которые приводят к возникновению резонансных колебаний.
В ходе анализа выяснилось, что резонансные колебания приводят к ударным контактным взаимодействиям между поверхностями ограничителей хода. Уровни механических напряжений в момент удара превышают предельное значение, что может быть причиной разрушения металлоконструкций. Подтверждение этому мы обнаружили в ходе повторного осмотра установки: на момент осмотра на ряде ограничителей хода отсутствовали резиновые демпферы; два торцевых ограничителя хода пластически деформированы, что свидетельствует об ударах в ходе эксплуатации.
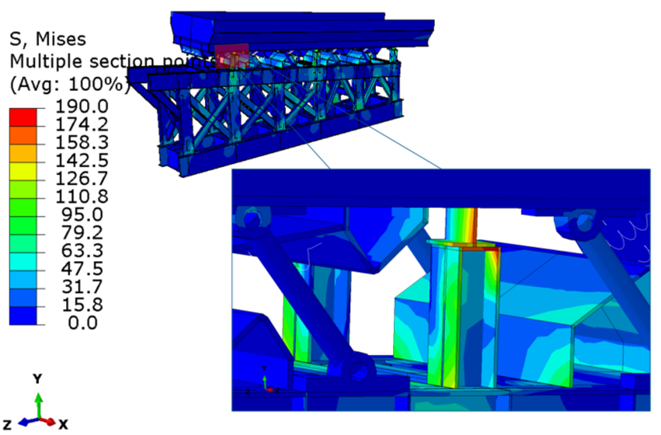
Нелинейный динамический анализ: распределение эквивалентных напряжений по Мизесу в момент удара по поверхностям ограничителей хода, МПа
По результатам работы мы сделали следующий вывод — наиболее вероятной причиной разрушения являются резонансные колебания конструкции и, как следствие, ударно-контактные взаимодействия по поверхностям ограничителей хода. О причинах возникновения резонансных колебаний по данным текущей модели (с учетом точности исходных данных) можно говорить лишь условно: работа двигателя на нерасчетных частотах вращения; износ редуктора и приводных механизмов, повлекших за собой изменение частоты воздействия внешней нагрузки; «усталость» пружин. Работа еще не завершена, сейчас мы проводим уточнение модели с использованием обновленных исходных данных.
С точки зрения применения метода конечных элементов (МКЭ) для решения практических задач в промышленности, этот проект наглядно демонстрирует что:
- МКЭ позволяет исследовать и анализировать процессы, которые нельзя наблюдать физически, например, из-за ограничения доступа в целях безопасности, условий среды или процессы, происходящие замкнутых объемах;
- анализ, проводимый с использованием МКЭ при достаточно точном воспроизведении реальной физики процесса, позволяет обнаружить критичные параметры процесса, даже если они не были сформулированы в первоначальных гипотезах;
- одним из основных ограничений практического применения МКЭ является недостаточное качество исходных данных, с которым мы сталкиваемся в большинстве наших проектов.
Для любителей технической информации сообщаем, что эта работа была проведена с использованием программного обеспечения SIMULIA Abaqus на расчетной станции Lenovo ThinkStation P720 (процессор Xeon Silver 4108, 128 Гб оперативной памяти). В зависимости от типа анализа (статический или динамический), размерность численных моделей составила от 50 до 300 тысяч конечных элементов; продолжительность расчета моделей составляет около нескольких минут для статического анализа и до часа для динамического. В целом вся работа от начала сбора исходных данных до формирования отчета и выдачи рекомендаций заняла 1 месяц.
Эта статья написана в соавторстве с моим коллегой Дмитрием Нуштаевым, инженером-прочнистом, к.т.н.
