Циклоидный редуктор + BLDC мотор своими руками07.06.2023 12:17

Всем привет! Эта статья открывает собой серию статей по разработке манипулятора. Тут я попробую рассказать о циклоидном редукторе и зачем он вообще мне понадобился. Разумеется, мы проведём его расчёт и воплотим его в физическое представление при помощи PLA пластика. Ну и как бонус соберём из хлама BLDC мотор для тестирования этого редуктора. Погнали.

Введение

Появилась идея собрать манипулятор. Я пока не определился с областью его применения. Будет ли это рука или какой-то захват, но есть одно требование — он должен быть точным, без люфтов, дрожаний и прочих радостей.

Для построения такого механизма обычные сервоприводы не пойдут. Под нагрузкой они имеют свойство терять в точности и имеют люфты из-за многоступенчатого редуктора. Тут мне на глаза попался циклоидный редуктор:

Он имеет довольно интересные свойства:

высокое передаточное отношение при относительно небольших габаритах;
отсутствие люфтов;
плавность хода;
высокие требования к точности изготовления.

Я решил попробовать его собрать и посмотреть его в деле. Давайте окунёмся в расчёты этого зверя и посмотрим, что получится при печати его на 3D принтере.

Расчёт редуктора

Подходов к расчётам много и каждый кусок приходилось искать отдельно. Я постарался собрать наиболее простой в одном месте не только для вас, но и для себя. Вот основные детали, которые нам нужно будет рассчитать и изготовить:

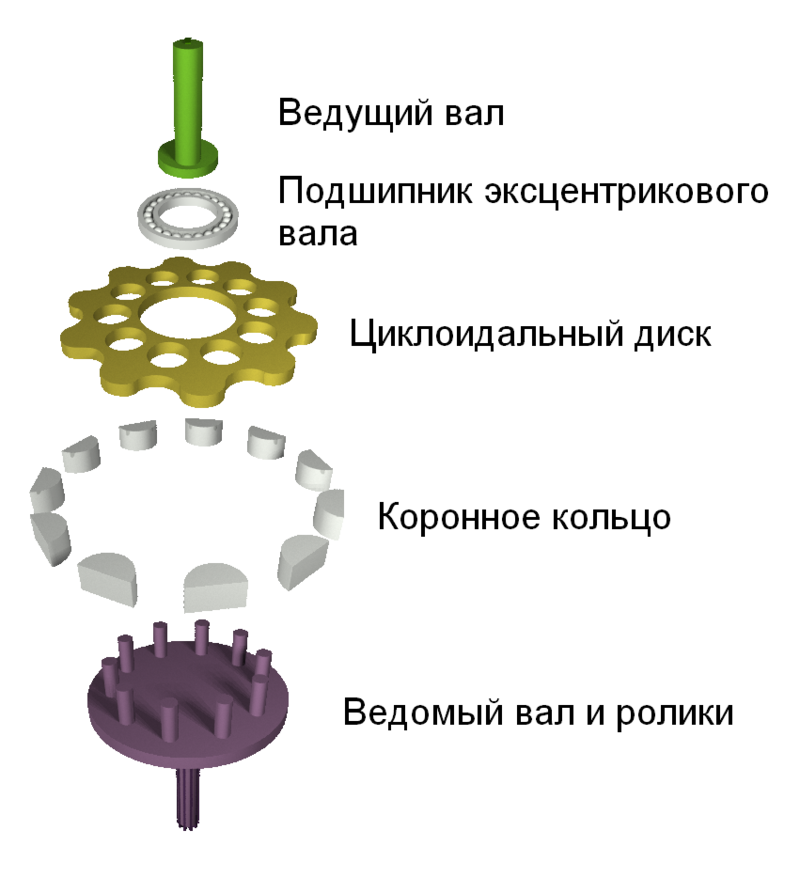
Детали редуктора

▍ Расчёт параметров коронного кольца

Начнём с выбора передаточного отношения, ну пусть будет 50. В результате мы получим снижение оборотов ведомого вала в 50 раз относительного ведущего, но получим увеличение в 50 раз крутящего момента. Из значения передаточного отношения можно получить количество зубьев коронного кольца и циклоидального диска:

$i=\frac{n}{N-n} \qquad (1.1)$

где n — количество зубьев циклоидального диска, N — количество зубьев коронного кольца. При этом должно соблюдаться условие:

$N = n+1 \qquad (1.2)$

Подставив формулу (1.2) в формулу (1.1) мы сможем получить количество зубьев циклоидального диска:

$$ i=\frac{n}{(n + 1) - n} => i= n \qquad (1.3) $» /> Получается, что отношение задаётся только количеством зубьев циклоидального диска. Всё очень просто. Для нашего случая n = 50, а по формуле 1.2 мы получаем N = 51. Далее нам нужно выбрать диаметр коронного кольца. Центры зубьев располагаются на его окружности, соответственно, от его будет зависеть диаметр зубьев (2.1), а у нас их целых 51. Тут можно считать в обе стороны: либо мы выбираем диаметр коронного кольца и считаем диаметр зубьев (2.1), либо, наоборот — относительно диаметра зубьев вычисляем диаметр коронного кольца (2.2). <div><img src=$

Коронное кольцо

$D_{зкк}=\frac{2\pi D_{кк}}{4N} \qquad (2.1)$

$D_{кк}=\frac{4ND_{зкк}}{2\pi } \qquad (2.2)$

Я выбрал путь 2.2 и взял для расчёта диаметр зубьев 2.5 мм. Мой принтер без проблем осилит такие зубья с высокой точностью.

$D_{кк}=\frac{4ND_{зкк}}{2\pi } = \frac{4*51*2.5}{2*3.14159} =81.2$

Ведущий вал редуктора вращается с небольшим смещением от оси вращения двигателя, это смещение называется эксцентриситет. Его значение вычисляется по формуле ниже (3.1):

$e=\frac{D_{зкк}}{4}=\frac{2.50}{4}=0.625 \qquad (3.1)$

▍ Расчёт и построение циклоидального диска

Тут мы внезапно переходим к построению циклоидального диска! Это нормально, хотя мы расчёты мы вели для коронного кольца, они нам ещё нужны :). Форма его зубьев представляет собой эпитрохоиду. Как она строится, показано ниже:

Построение эпитрохоиды

Рассчитаем диаметр окружности, при помощи которой мы будем строить эпитрохоиду (4.2). Далее я её буду называть ОЭО — описывающая эпитрохоиду окружность (чёрная на анимации). И диаметр окружности, по которой будем катать ОЭО (4.1). Далее её я буду называть ОЭ — окружность эпитрохоиды.

$D_{оэ}=\frac{nD_{кк}}{N}=\frac{50*81.2}{51}=79.6 \qquad (4.1)$

$D_{оэо}=D_{кк} - D_{оэ}=81.2-79.6=1.6 \qquad (4.2)$

Нам нужно параметрическое уравнение эпитрохоиды. Выглядит оно следующим образом (4.3), (4.4).

$x=(R_{оэ}+R_{оэо})\cdot cos(t) - e\cdot cos(\frac{(R_{оэ}+R_{оэо})t}{R_{оэо}}); 0 < t <2\pi \qquad (4.3) \\ y=(R_{оэ}+R_{оэо})\cdot sin(t) - e\cdot sin(\frac{(R_{оэ}+R_{оэо})t}{R_{оэо}}); 0 < t <2\pi \qquad (4.4)$

Теперь мы можем приступить к построению эпитрохоиды. Делать это мы будем при помощи параметрического уравнения и соответствующей функцией CAD (спасибо 21 век). Для проектирования я использую КОМПАС 3D, там есть функция «Кривая по закону» в разделе «Каркас и поверхности».

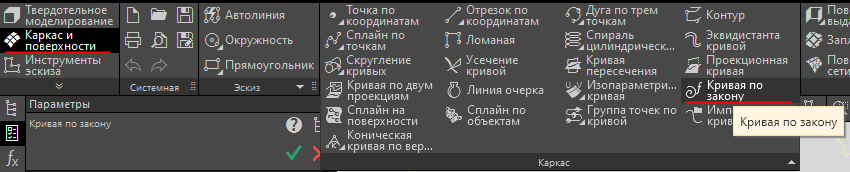
Меню «Каркас и поверхности»

В открывшемся окне можно указать уравнения для X, Y, Z. Очень важно все расчёты проводить без округления, т. к. выражение внутри второго cos\sin имеет огромное влияние на построение. Малейшие отклонения даже в тысячных приведут к тому, что конец кривой в итоге не сойдётся с её началом. Получились такие страшные уравнения:

$x=(39.7887+0.795775)*cos(t) - 0.625*cos((39.7887+0.795775)/0.795775 * t) \\ y=(39.7887+0.795775)*sin(t) - 0.625*sin((39.7887+0.795775)/0.795775 * t)$

Но в итоге получаем красивую кривую. Всё же математика не перестаёт удивлять :)

Эпитрохоида циклоидального диска

Но это ещё не всё. Теперь нам нужно построить эквидистанту этой кривой на расстояние половины диаметра зуба коронного кольца (Dзкк), который мы выбрали ранее (2.5 мм). Направление построения внутрь кривой.

В КОМПАС 3D для этого нужно спроецировать эту кривую на плоскость, т. к. она изначально строится в трёхмерном пространстве, потом построить эквидистанту проекции на расстоянии -1.25 мм и спроецировать эквидистанту на эскиз. Немного сложно, но другого способа я не нашёл, возможно, можно проще.

В итоге мы получаем эскиз, в котором мы можем делать с этой кривой всё что угодно. И первым делом мы преобразовываем её в сплайн вот с такими параметрами (картинка ниже). С другими параметрами получаются странные артефакты.

Параметры сплайна

Без преобразования в сплайн при копировании кривой и последующей её вставки в другую деталь, кривая изменяет свою форму (наверное бага). И программа почему-то очень долго обрабатывает операцию выдавливания для исходной кривой. Сплайн решает эти проблемы.

В результате мы получаем форму циклоидального диска (бежевая линия на картинке).

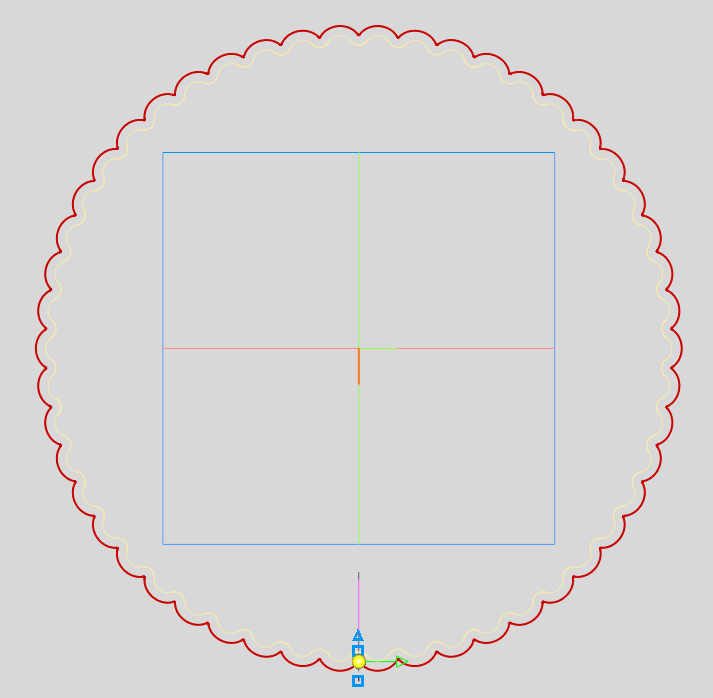
Эквидистанта эпитрохоиды

Не забываем добавить посадочные места под подшипники входного вала с эксцентриком и ролики выходного вала. Размеры посадочных мест выбираются исходя из требуемых типов подшипников (в моём случае это те, что есть в коробке). Выдавливаем всё это дело и получаем такое красивое колесо. Центральный подшипник я взял размером 24×12х6, а подшипники под выходной вал размером 10×5x4.

Циклоидальный диск

▍ Построение коронного кольца

Давайте теперь построим коронное кольцо. Лучше всего это делать после построения циклоидального диска, т. к. на этом этапе можно проверить правильность расчётов. Строим окружность диаметром $D_{кк}=81.2$ и располагаем на нём N = 51 окружность диаметром $D_{ккз}=2.5$ .

Эскиз коронного кольца

Теперь мы берём контур нашего циклоидального диска и его центр располагаем на расстоянии эксцентриситета от центра коронного кольца.

Эскиз коронного кольца

Вот тут можно и проверить правильность расчётов. Зубья циклоидального диска не залезают за контур будущих зубьев коронного кольца — мы сделали всё правильно и механизм будет работать. Дальше есть 2 пути: мы оставляем зубья коронного кольца в виде окружностей или делаем из них что-то вроде зубчатого колеса. Я выбрал второй вариант и при помощи скругления между окружностями соединил зубья в единую сущность.

Можно в качестве зубьев использовать головки болтов ИМБУС, но зубьев довольно много и я решил, что лучше и быстрее будет их напечатать.

Модель коронного кольца

▍ Расчёт и построение выходного вала и эксцентрика

Ну вот мы подобрались к последним элементам редуктора — выходному валу и эксцентрику. Давайте начнём с эксцентрика, т. к. это самая простая деталь. Он должен насаживаться на вал двигателя и иметь смещение от центра его вращения, мы его вычисляли по формуле (3.1). Всё просто.

Эксцентрик

Получилась очень простая деталь, которая запрессовывается в центральный подшипник циклоидального диска.

Эксцентрик

А вот выходной вал придётся немного посчитать. У него имеются штифты, которые взаимодействуют с циклоидальным диском и преобразуют его несоосное движение в соосное относительно оси вращения двигателя. Диаметр штифтов вычисляется следующим образом:

$D_{ш}=D_{о}-2e=5-2*0.625=3.75 \qquad (5.1)$

где $D_{о}$ — диаметр отверстия под штифт на циклоидальном диске. В нашем случае это внутренний диаметр подшипника 5 мм, $ e $ — значение эксцентриситета.

Количество штифтов определяется нагрузкой на выходной вал. Чем выше нагрузка, тем больше штифтов понадобится. Во время работы редуктора штифты работают на излом, т. к. сила прикладывается к ним перпендикулярно к их оси, соответственно, они должны иметь большую прочность. Пластик тут нам не может.

В качестве штифтов я использовал болты М4, срезал с них головку и слегка сточил резьбу дремелем, чтобы примерно быть рядом с 3.75 мм. Окружность, на которой находятся центры штифтов — должна совпадать с окружностью, на которой находятся центры отверстий под них на циклоидальном диске (где располагаются подшипники).

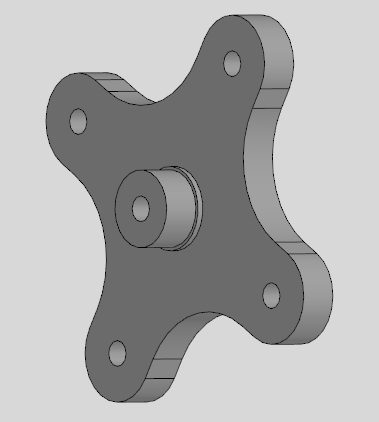
Выходной вал

▍ Печать, печать, печать…

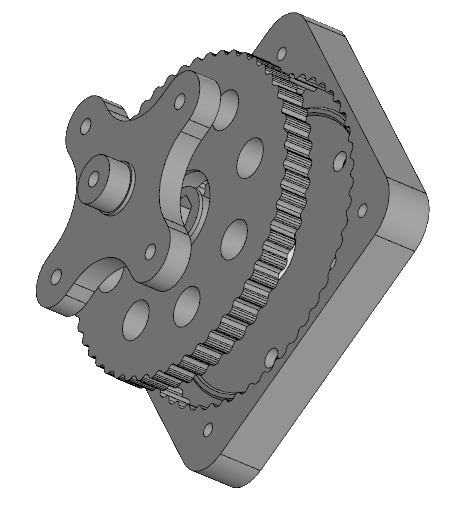
Сборка редуктора

Коронное кольцо, он же корпус с эксцентриком на валу двигателя

Циклоидальный диск с подшипниками

Выходной вал с установленными штифтами

Насаживаем циклоидальный диск на эксцентрик

Устанавливаем выходной вал

Закрываем крышкой и фиксируем ось выходного вала подшипникомВо время тестов на видео слышны закусывания, это как раз из-за неточности изготовления. Деталь после печати изменяет свои геометрические размеры из-за усадки пластика.

Очень интересный принцип его работы. Получается, что за один оборот двигателя циклоидальный диск делает шаг на один зуб, но тут и кроется его беда. За счёт наличия эксцентрика у этого редуктора большие вибрации на высоких оборотах, что сужает спектр решаемых им задач (спойлер).

BLDC мотор

После создания редуктора хотелось бы его проверить на высоких оборотах. У меня не нашлось подходящих двигателей для него, и я решил собрать свой. Выбор пал на радиальный бесщёточный мотор из-за его конструкции — он плоский и его удобно состыковать с редуктором.

Для его сборки были заказаны неодимовые круглые магниты диаметром 20 мм и толщиной 3 мм, ну и катушка намоточной проволоки диаметром 0.5 мм. Конфигурацию двигателя я выбрал исходя из размеров редуктора, получилось 8 магнитов и 6 катушек.

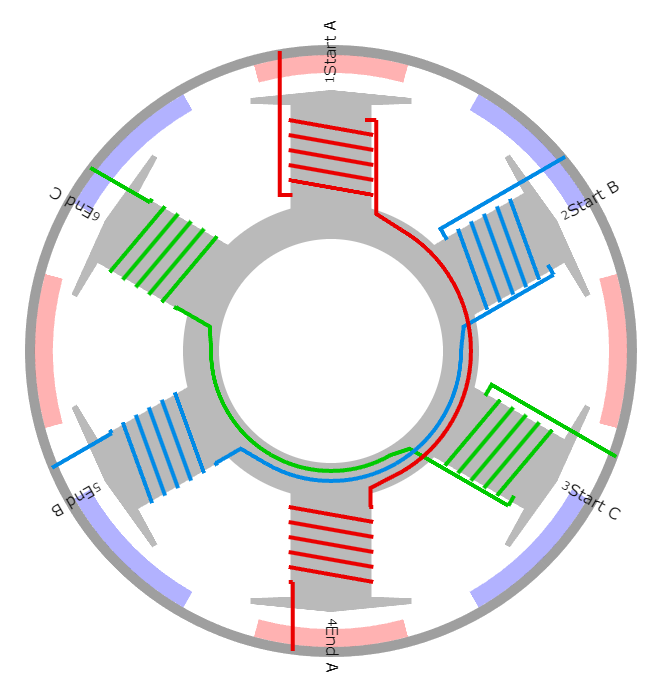
Схема двигателя

Собираем ротор. Он представляет собой кусок пластика с посадочными местами под магниты и отверстием под вал. В качестве вала я использовал болт М5. Магниты необходимо проклеивать, так как есть большая вероятность их вылета из посадочных мест. В результате могут повредиться обмотки или можно получить травмы.

Есть важная особенность при проектировании таких моторов — магниты должны быть как можно ближе друг к другу. В идеале это должно быть намагниченное кольцо. В первой итерации я расположил магниты слишком далеко и происходил срыв синхронизации, мотор просто не работал.

Ротор с магнитами

Ну теперь самое весёлое — намотка катушек. У меня получилось 7 слоёв по 8 витков, суммарно 56 (в среднем, т. к. есть небольшие отклонения в 1–2 витка). Каждый слой я покрывал лаком для прочности обмотки, так как её без проблем может размотать магнитным полем. Изначально я хотел 9 катушек, но терпения у меня хватило только на 6. Блок питания у меня слабоват и не вытягивает токи больше 2 А, поэтому обмотки соединены звездой для снижения пусковых токов и плавности хода.

Обмотка двигателя

Закидываем обмотки в статор, фиксируем пайку термоклеем, выводим провода от обмоток для подключения регулятора и запрессовываем два подшипника по пути.

Статор с обмотками

Пришло время накинуть ротор. Он немного выступает из корпуса — это нормально, сверху ещё будет защитный кожух. Мотор развивает очень большие обороты и довольно страшно держать его в руках, когда есть риск разрушения всех этой конструкции. Расстояние между катушками и магнитами около 1.5 мм, что довольно много, но для MVP вполне сойдёт. Пластик — это не тот материал, из которого нужно изготавливать моторы, так как сказывается его мягкость.

Двигатель в сборе

Во время первых тестов было весело. «А давай попробуем на максимальные обороты его вывести», подумал я:

Докрутились

Плохо промазал верхние слои и в результате витки приподняло магнитным полем, ну, а дальше и так понятно. Было страшно. Но нечего, перематываем 2 обмотки, промазываем, меняем их и погнали дальше.

Ну и, конечно же, результат. Ток холостого хода составил 270 мА, рукой остановить очень сложно. Учитывая, что тут статор собран без использования металла, результат очень хорош, по крайней мере, я доволен. На видео всего 30% мощности, т. к. без кожуха я не рискнул его разгонять на 100%.

▍ Результаты и заключение

На видео видно, что при высоких оборотах наблюдается сильная вибрация. Также слышен сильный шум во время работы редуктора, вызванный неточностью изготовления штифтов выходного вала. В результате этого во время работы штифты начинают биться о подшипники, а должны были скользить по ним.

Какие выводы из всего этого можно сделать?

Люфт элементов редуктора сильно зависит от точности изготовления (кто бы сомневался);
Сильные вибрации на высоких оборотах. Такой редуктор будет отлично работать с шаговыми двигателями, что я и буду делать;
Удержание положения из коробки. Редуктор очень сложно провернуть путём вращения выходного вала;
Компактные размеры при больших передаточных отношениях, если сравнивать с обычными редукторами на зубчатых колёсах;
Относительная простота расчётов и проектирование 3D модели (тут спорно, т. к. современные CAD умеют сами строить большинство известных передач, вплоть до планетарных редукторов)

В целом, для решения моих задач его возможностей достаточно. Попробуем его в реальном проекте. В следующей статье попробуем собрать сервопривод на основе циклоидального редуктора и шагового двигателя. Надеюсь, было интересно. Спасибо за внимание!