Цифровой водяной знак на основе дискретного Wavelet-преобразовании28.11.2021 21:46

Тема защиты авторских прав в нынешнее время стала максимально востребованной, появилось множество способов не допустить нелицензионного тиражирования, Один из таких способов — цифровой водяной знак (англ. Digital Watermarking, ЦВЗ), добавление к исходной информации (цифровому изображению, видео- или звуковому файлу) некоторых скрытых маркеров, устойчивых к каким-либо атакам. В основном Digital Watermarking используют для определения факта нарушения авторских прав, но, конечно же, сфера применения цифровых водяных знаков этим не ограничивается. Например, цифровые водяные знаки могут использоваться для передачи секретной информации, проверки подлинности электронных документов и в ряде других приложений. Во многих приложениях и сайтах внедрена защита видеопродукции при помощи ЦВЗ, где происходит построение множества идентификационных меток, внедрение одной из меток в видеопоследовательность, извлечение метки из пиратской копии видеопоследовательности, поиск участников коалиции по извлеченной метке.

Давайте рассмотрим внедрение и проверку цифрового водяного знака на примере работы алгоритма дискретного wavelet-преобразования для изображения.

Дискретное wavelet-преобразование

Дискретное wavelet-преобразование раскладывает сигнал на взаимно ортогональный набор вейвлетов (математических функций, позволяющих анализировать различные частотные компоненты данных), что является основным отличием от непрерывного вейвлет-преобразования. Вейвлет может быть сконструирован из функции масштаба, которая описывает свойства его масштабируемости. Ограничение состоит в том, что функция масштаба должна быть ортогональна своим дискретным преобразованиям, что подразумевает некоторые математические ограничения на них:

$φ(x)=\sum_{k=-∞}^∞a_kφ(Sx-k).$

где — фактор масштаба (у нас он будет равен 2), более того, площадь под функцией должна быть нормализована, и функция масштабирования должна быть ортогональна, поэтому:

$\int_{-∞}^∞ φ(x)φ(x+l)dx=δ_{0,l}$

После введения некоторых дополнительных условий (поскольку вышеупомянутые ограничения не приводят к единственному решению) мы можем получить результат этих уравнений, т.е. конечный набор коэффициентов a_k которые определяют функцию масштабирования, а также вейвлет. Набор вейвлетов затем формирует ортонормированный базис, который мы используем для разложения, обычно только несколько коэффициентов a_k будут ненулевыми, что упрощает расчёты.

Схема работы алгоритма

Давайте рассмотрим схему работы на растровом изображении.

Зададим двумерный массив , имеющий размеры (2^n+1)×(2^n+1) , обозначающий яркость конкретной координаты по одному из цветов ( B[x,y] — яркость пикселя с координатами (x,y) для всех x,y = 0..2^n )

Далее давайте рассмотрим -й шаг: создадим четыре массива (модель двумерного wavelet-преобразования):

$B_i[x,y] = B_{i-1}[2x,2y]$ $H_i[x,y] = B_{i-1}[2x+1,2y] - \frac{1}{2}(B_{i-1}[2x,2y]+B_{i-1}[2x+2,2y]),$ $V_i[x,y] = B_{i-1}[2x,2y+1] - \frac{1}{2}(B_{i-1}[2x,2y] + B_{i-1}[2x,2y+2],$ $C_i[x,y] = B_{i-1}[2x+1,2y+1] - \frac{1}{4}(B_{i-1}[2x,2y] + B_{i-1}[2x+2,2y] + B_{i-1}[2x,2y+2] + B_{i-1}[2x+2,2y+2]),$

Для всех $x,y = 0..2^{n-i}$ .

Здесь H_i означает отклонение яркости точки с координатами (2x+1,2y) от среднего арифметического яркостей двух соседних по горизонтали точек (2x,2y) и (2x+2,2y) (рис. 1),

V_i означает отклонение яркости точки с координатами (2x,2y+1) от среднего арифметического яркостей двух соседних по горизонтали точек (2x,2y) и (рис. 2),

C_i означает отклонение яркости точки с координатами (2x+1,2y+1) от среднего арифметического яркостей четырех соседних точек. (рис. 3)

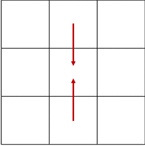Рис.2 Рис. 2 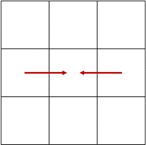Рис.1 Рис. 1 Рис.3 Рис. 3

Далее мы «обновляем» точки массива B_i :

$B_i[x,y] = B_i[x,y] + \frac{1}{4}(H_i[x,y]+V_i[x,y] + C_i[x,y].$

Обновление нужно для того, чтобы средняя энергия изображения B_i (его средняя яркость) была равна средней яркости исходного массива. Очевидно, что изображение $B_{i-1}$ , и как следствие, однозначно восстанавливается. Стоит также заметить, что каждый раз, когда мы вычисляем новые элементы H_i , V_i , C_i , мы можем больше не запоминать те, что использовали для их вычисления ( $B_{i-1}[2x+1,2y]$ , $B_{i-1}[2x,2y+1]$ , $B_{i-1}[2x+1,2y+1]$ ). Это значит, что наш алгоритм не привлекает дополнительной памяти.

Выполняем наши шаги до того момента, пока наш массив не будет размера (2×2) . То есть, теперь мы имеем и наборы H_1 , V_1 , C_1 ; H_2 , V_2 , C_2 ;…; H_n , V_n , C_n

Заметим, что H_i , V_i , C_i влияют только на 2^i+1 пикселей, таким образом, каждый шаг соответствует разной степени резкости (детализации). Например, для i=1 каждый коэффициент влияет на всего лишь 3 пикселя, если i = 2 то на 5 и т д.

Попробуем теперь внедрить наш ЦВЗ в изображение, для этого мы выбираем α∈(0,1) — «заметность» водяного знака, резкость - шаг и массив , или , на котором и будем введен водяной знак.

Пусть для определенности это будет H_k , тогда заменим его на массив $H_k^{'}$ , такой что:

$H_k^{'}[x,y]=(1-α)H_k[x,y]+αW[x,y].$

Здесь W_k , и как следствие $H_k^{'}$ , имеет тот же размер, что и H_k . W_k можно назвать коэффициентами wavelet-преобразования другого изображения B^w .

Произведем обратное wavelet-преобразование и получим новое изображение, назовем его $B^{'}$ .

Теперь, давайте поговорим о том, как автор, имея только B^w , или еще проще сами коэффициенты W_k[x,y] , их легко вычислит, зная все остальное), параметр , в какой массив внедрялся и заметность , сможет проверить наличие ЦВЗ.

Зная исходное изображение, можно проверить, помечено ли наше изображение, просто сравнивая разность коэффициентов и массив .

Теперь рассмотрим случай, когда нам не известно изображение-оригинал и, по этим же причинам $B^{'}$ . Тогда мы не можем точно сказать, использован ли тут ЦВЗ, но можем оценить вероятность его нахождения. Для этого мы предположим, что наше изображение осмысленное, то есть не является хаотичным распределением яркостей пикселей. Соответственно массив H_k , предположительно несущий в себе водяной знак и напрямую связанный с изображением, тоже являет собой некоторую упорядоченную структуру. Значит, что H_k до добавления в него αW_k был более не менее упорядоченной структурой, значит, что нам надо для H_k-αW_k (с точностью до коэффициента 1-α ) ввести меру упорядоченности — сложности. Вполне подходит вариация функции. Действительно, чем меньше резких перепадов функции, тем меньше ее вариация. Для двумерного массива введем аналог вариации:

$Var(H_k)=\sum_{x,y = 0}^{2^{n-k}-1}(|H_k[x,y]-H_k[x+1,y]|+|H_k[x,y]-H_k[x,y+1]|).$

Давайте поймем, как можно применить данную функцию: как и описывалось ранее, если H_k — результат нанесения водяного знака ( αW_k ), то он будет более сложным, чем H_k-αW_k , значит будет выполняться:

Var(H_k)>Var (H_k-αW_k).» src=«https://habrastorage.org/getpro/habr/upload_files/6eb/d1b/e7b/6ebd1be7bf74deb94619768d872819a5.svg» /></p>

<p>Для более надежной работы алгоритма, можно ввести порог, после которого будем считать, что ЦВЗ обнаружен, если </p>

<p><img alt= βαVar (W_k),» src=«https://habrastorage.org/getpro/habr/upload_files/f24/2f8/1df/f242f81df7aa494fe3782689692cb047.svg» />

где значение αVar(W_k) будет соответствовать максимально возможному увеличению вариации при добавлении αW_k к массиву H_k , а -параметр подбирается экспериментально.

Заключение

Стоит сказать, что приведенный алгоритм на основе дискретного wavelet-преобразования лишь один способ из многих, которыми можно осуществить внедрение цифрового водяного знака и проверить наличие такового в файле. Например, для текста можно использовать кодирование со сдвигом строки, для изображения — водяные знаки домена DСT, а для звука — кодирование с наименьшей значимостью. Преимущество приведенного выше алгоритма заключается в том, что такие водяные знаки устойчивы по отношению к сжатию JPEG (для изображений) и некоторым другим искажения, вот почему данный метод остается актуальным и по сей день.

В скором времени я дополню статью кодом, реализующий приведенный выше алгоритм.