Честное онлайн-голосование: миф или реальность?
Привет, Хабр! Меня зовут Иван, я разрабатываю сервис онлайн-голосований WE.Vote на основе блокчейн-платформы Waves Enterprise. Сама идея голосований в онлайне уже давным-давно реализована разными компаниями, но в любых кейсах «повышенной ответственности» все равно прибегают к старой доброй бумаге. Давайте посмотрим, как электронное голосование сможет посостязаться с ней в максимально строгих условиях.

Идея проведения онлайн-голосований не нова. Появляются соответствующие сервисы, но традиционное очное голосование на бумажных бюллетенях все еще является наиболее распространенным способом принятия важных коллективных решений. Например, в национальных выборах с миллионами бюллетеней, тысячами избирательных участков, наблюдателей и волонтеров. Или на собраниях акционеров крупного общества, где даже на стадии уведомления о грядущем собрании нужно разослать вагон заказных писем и убедиться что они были получены. Или на общих собраниях собственников дома, где приходится ловить момент, когда каждый из жильцов не на работе, не в отпуске и не на даче, чтобы с опросным листком обойти все квартиры. Да, «бумага» — это долго и дорого. Но несмотря на все недостатки «бумажного» голосования, она продолжает активно использоваться — частично в силу инерционности регулирующего законодательства, и, наверное, в большей степени из-за веры в надежность традиционных, устоявшихся процедур.
Тем не менее дистанционные решения возникают и отвоевывают себе место под солнцем. Онлайн-голосования набирают популярность и в государственном, и в корпоративном секторе. На стороне «онлайна» очевидные преимущества в плане эффективности — людям, находящимся в разных уголках мира, гораздо проще и дешевле разослать бюллетени в электронном виде, чем собирать их в арендованном конференц-зале. Пандемия добавила нюансов в виде необходимости «социального дистанцирования», еще больше подсветив преимущества методов дистанционного принятия решений.
Подавляющее большинство сервисов онлайн-голосований — это централизованные решения, управляемые конкретной компанией-оператором. Есть ли здесь угрозы конфиденциальности и манипуляций? С технической точки зрения понятно, что оператор такой системы имеет доступ ко всем ее данным. Соответственно, теоретически у него есть возможность вмешаться в ход голосования или подправить результаты. Но многие решения, используемые бизнесом, опираются на доверие — и в этом нет ничего страшного.
Системы выстраиваются не на «технической невозможности», а на «экономической нецелесообразности» вмешиваться в бизнес-процессы клиентов. Может ли банк подправить баланс вашего счета? Может. Станет ли он это делать? Скорее всего, не станет (но это неточно). Вокруг подобных сервисов выстраивается юридическая инфраструктура в виде договоров между клиентом и оператором сервиса, соглашений о неразглашении, государственное регулирование и т.д. В результате получается вполне рабочая история: бизнес делает свое дело, оператор сервиса онлайн-голосований помогает бизнесу принимать решения. Но, кажется, осадочек остается.
Но что если вам нужно больше? Что если одновременно нужна экономическая эффективность, конфиденциальность принимаемых решений и максимальная «теоретическая невозможность» для оператора сервиса онлайн-голосований повлиять на их результат? Представьте гипотетическую ситуацию, в которой одна глобальная корпорация «Кэппл» принимает решения о своей глобальной стратегии развития на инфраструктуре другой глобальной корпорации «Тубель». Сколько бы соглашений и договоров ни было подписано — удержится ли «Тубель» от возможности подсмотреть, о чем там договаривается его прямой или косвенный конкурент? Будет ли менеджмент «Кэппла» спать спокойно, будучи уверенным, что никто не вмешается в их прорывные планы развития?
Стоит ли, положившись на идеальность нашего мира, отвечать на оба вопроса «да»? Или мы можем создать техническое решение, отвечающее всем требованиям? Давайте посмотрим.
Чего мы хотим добиться
На самом абстрактном уровне всё, что делают информационные системы, — это создают/изменяют данные, передают данные, хранят данные, а также дают доступ к этим данным. В применении к онлайн-голосованиям это выглядит следующим образом:
Организатор голосования создает повестку и хочет управлять правилами доступа к этой повестке: сделать ли ее публичной или раскрыть только участникам голосования.
Организатор голосования создает список его участников и хочет быть уверенным, что в его голосовании примут участие именно они. Сами участники также заинтересованы в этом, так как подразумевается, что они принимают решение по важному для них вопросу и мнение/намерения/выгода третьих лиц не должны на это решение повлиять.
Организатор задает правила проведения голосования. Эти правила — без раскрытия сути голосования — должны быть доступны широкой публике, чтобы организатор, участники голосования и третьи лица (например, регулятор) могли убедиться, что способ принятия решения был выбран корректно и все прошло по заранее известному плану.
Участник голосования получает повестку голосования и хочет убедиться, что это именно тот список вопросов, который получат все остальные, что ему не прислали «укороченную версию». Эти сомнения выглядят нелепо для бумажного голосования, где все бланки заранее распечатаны, все выдаются из общей стопки и нет никакой возможности «персонализировать» бюллетень. Но в случае онлайн-голосования все, что мы имеем, — это байты информации, которые легко изменить на лету. Поэтому хотелось бы иметь больше гарантий аутентичности.
Участник голосования заполняет бюллетень и хочет убедиться, что его голос будет учтен, его голос не будет изменен и никто не сможет определить, как именно он проголосовал (частный случай открытых голосований оставим в стороне).
Организатор и участники голосования узнают его результаты. В этот момент все хотят быть уверены, что никто не вмешивался в ход голосования, не фильтровал бюллетени, не делал вбросов, не подправлял итоги и т.п. Все — включая и оператора онлайн-сервиса голосований.
При чем тут блокчейн
Если бегло пробежаться по первому разделу, то единственной проблемой онлайн-голосований выглядит всевластие оператора сервиса голосования. Хорошая новость в том, что с появлением блокчейна мы научились ограничивать эту власть, разделяя ответственность за данные системы между ее участниками. Но очевидно, что блокчейн не является серебряной пулей. По сути, это сравнительно медленная и капризная база данных — инструмент, имеющий определенные положительные свойства и некоторые недостатки. Чтобы полностью решить задачу, необходимо правильно определить роль блокчейна в системе, понять, чего еще нам недостает. И кажется, у нас получилось сложить кусочки пазла — посмотрим как.
Распределенное хранение
С ходу напрашивается решение использовать блокчейн для хранения данных голосования. Так при правильном развертывании сети блокчейн-узлов мы сможем не беспокоиться о том, что оператор сервиса единолично подменит записанные данные. Проблема надежного хранения исторической информации решена.
Дополнительно мы можем решить вопрос аутентичности данных: вся информация, которая попадает в блокчейн (в виде транзакций) должна быть подписана отправителем. Публичный ключ участника процесса становится его внутрисистемным идентификатором, а подпись на отправленной транзакции доказывает, что именно он ее отправил.
Естественно, встает вопрос хранения конфиденциальных данных. Блокчейн сам по себе не позволяет таких фокусов, поэтому нам надо разобраться, какие данные в системе являются открытыми, а какие приватными. А также найти методы защиты конфиденциальных данных. Например, при создании голосования мы имеем следующий набор данных:
повестка и материалы голосования;
контактные данные пользователей — идентификатор пользователей в реальном мире (e-mail или номер телефона);
персональные данные пользователей — в целом, в системе не требуются, но делают работу удобнее как для организатора голосования, так и для самих участников;
пара публичного и приватного ключей участника голосования — работают как внутрисистемный идентификатор пользователя и дают возможность участвовать в голосовании.
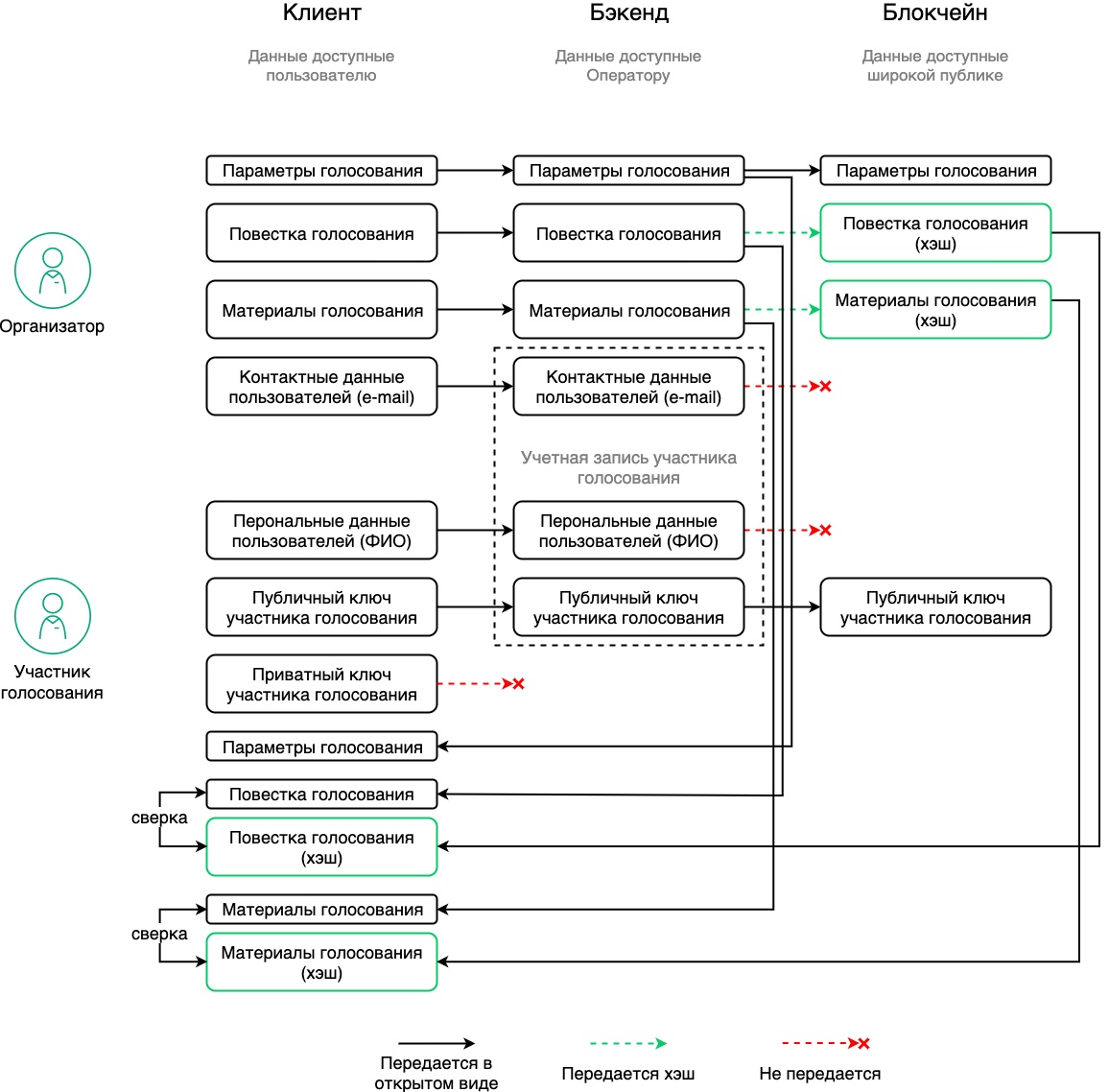
С повесткой и материалами голосования мы можем работать как любой другой облачный сервис: организатор голосования загружает их на сервер (бэкенд), и их доступность определяется ролевой моделью: участникам голосования мы их показываем, от остальных прячем. Для уверенности в том, что на бэкенде ничего с повесткой не произойдет, сохраним в блокчейне хеш от материалов, хранящихся на сервере. Организатор видит, что в голосовании зафиксировано именно то содержание голосования, которое он планировал, участники голосования при получении повестки также могут убедиться, что повестка эта у всех едина.
Персональные и контактные данные хранятся на сервере в виде учетной записи пользователя. Публиковать их на блокчейне было бы неправильно, и мы этого делать не будем. На блокчейне список участников голосования будет сохранен в виде списка публичных ключей.
Пара ключей создается пользователем локально, на его персональном устройстве. Приватный ключ этого устройства не покидает, а публичный сохраняется на бэкенде как параметр учетной записи. Организатор голосования работает со списком участников в виде Ф.И. О. и e-mail. При сохранении данных голосования в блокчейне туда же уходит список публичных ключей. Голос подписан ключом пользователя, и если публичный ключ отправителя есть в списке участников, мы принимаем бюллетень. Такая схема позволяет, с одной стороны, не светить персональными данными пользователей, а с другой — сделать более прозрачной работу системы.
Но с заполненными бюллетенями участников голосования простым хешированием не обойтись. Да, хеш бюллетеня на блокчейне спасет его от подмены —, но нам же надо будет ещё и посчитать результаты голосования. Чтобы работа системы не выглядела как цирковое представление, когда бюллетени и результаты появляются магическим образом из шляпы, попробуем сделать всё прозрачно и сохранить в блокчейн не только сам факт отправки голоса, но и его содержание. Естественно, таким образом, чтобы всё осталось конфиденциально.
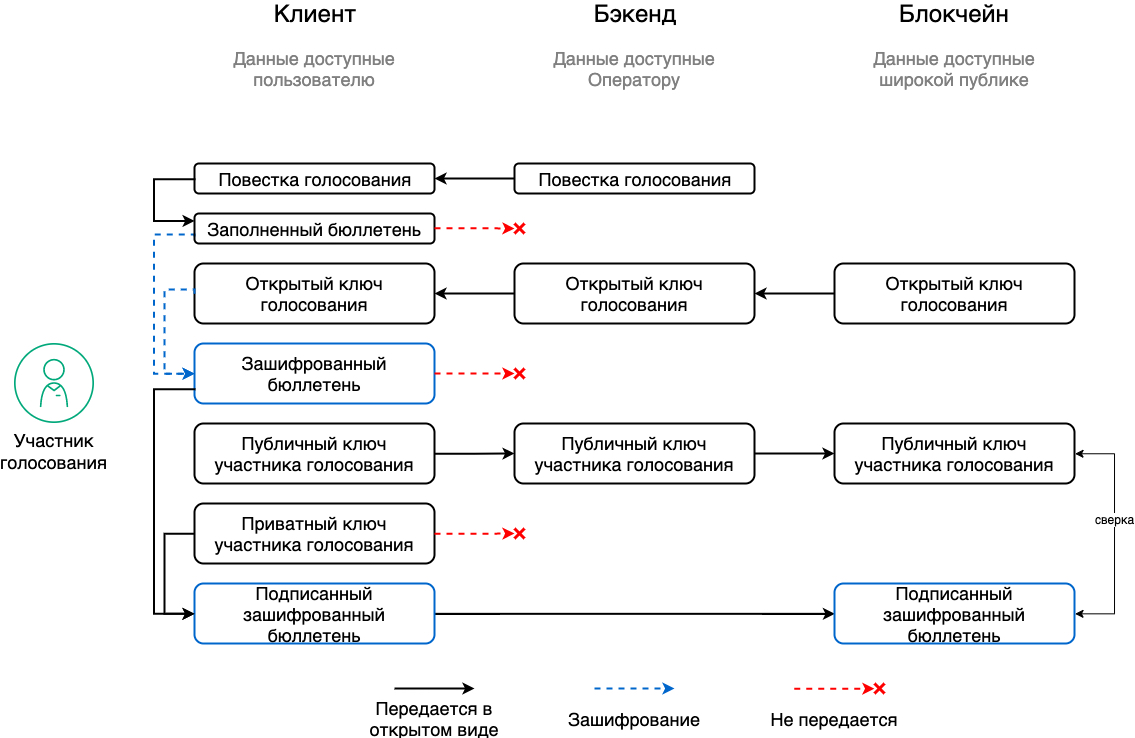
Получив бюллетень с сервера и убедившись, что повестка соответствует сохраненному в блокчейне хешу, участник голосования заполняет форму, затем шифрует его общеизвестным открытым ключом голосования и, наконец, подписывает своим приватным ключом (в формате блокчейн-транзакции). В результате этих манипуляций мы получаем заполненный бюллетень участника, который нельзя ни изменить (на нем стоит подпись), ни прочитать (он зашифрован).
Такой бюллетень можно только «потерять». Но у нас нет никаких оснований «потерять» именно этот бюллетень, так как мы не знаем за что голосовал пользователь, да и пропажа бюллетеня очень легко обнаруживается как самим голосующим, так и сторонними наблюдателями. Ведь в блокчейне виден и список зарегистрировавшихся участников голосования, и отправленные ими бюллетени. А распределенная природа блокчейна позволяет участнику голосования напрямую отправить транзакцию в любой из блокчейн-узлов, минуя бэкенд и любых других «посредников». Узел блокчейна совершенно не интересуется голосованиями или любыми другими процессами, которые мы пытаемся строить поверх блокчейн-сети. Всё, что интересует сеть, — это корректный формат транзакции: если всё верно, то транзакция, а значит и голос, будут зарегистрированы в блокчейне.
Подводя промежуточный итог, можно сказать, что:
Мы решили проблему прозрачности и immutable-хранения исторических данных, используя блокчейн.
Управление видимостью конфиденциальных данных мы организовали классическим централизованным образом, но внесли дополнительный механизм контроля информации на бэкенде — через хеши-«якоря», хранящиеся в блокчейне.
Работу с информацией об участниках голосования мы разделили. Персональные данные хранятся классическим образом, а взаимодействие происходит с уникальным блокчейн-идентификатором, от имени которого пользователь отправляет свой голос.
Но, несмотря на то что мы обещали обойтись без магии, она все-таки произошла. Для шифрования бюллетеней нам понадобился открытый ключ голосования, но никто не сказал, откуда он взялся! Очевидно, что это предельно важная часть всего процесса голосования и к нему нельзя отнестись легкомысленно. Еще более интересным кусочком пазла является приватный ключ, соответствующий открытому ключу голосования, так как именно с его помощью мы сможем получить итоги голосования. Настал момент шагнуть в область криптографии (которая для 99.9% людей не сильно отличается от магии).
Криптография
Итак, мы добились того, чтобы данные, сохраненные в системе, не могли быть изменены. Но до того, как данные попадут в блокчейн, существует достаточно просторное поле для злоумышленников, где они могли бы повлиять на исход голосования. Например, оговорка в предыдущем разделе о возможности «потерять» голос. У нас нет мотивации это сделать, если мы не можем прочитать зашифрованный бюллетень. Но что если все-таки можем?
Допустим, мы решили создавать ключ голосования на бэкенде, отправлять открытую часть всем участникам голосования и после завершения голосования использовать закрытую для расшифровывания? Даже на первый взгляд такая реализация выглядит ненадежно. Что помешает оператору системы (или злоумышленнику, попавшему на сервер) получить доступ к приватному ключу голосования, на лету расшифровывать бюллетени до их попадания в блокчейн и отфильтровывать «неправильно заполненные»? Или еще до начала голосования подкинуть свой открытый ключ голосования на сервер? Тогда только у злоумышленника будет соответствующий закрытый ключ и никто кроме него не получит итоги голосования. Что если в ходе голосования злоумышленник получит возможность расшифровывать попавшие в блокчейн бюллетени, получит доступ к промежуточным результатам голосования и каким-либо образом повлияет на итоговый исход?
Несколько более надежным вариантом будет техника разделения приватного ключа после генерации — хорошо известная схема разделения секрета Шамира. Ключевая пара создается, публичный ключ сохраняется в блокчейне как открытый ключ голосования, а приватный ключ разделяется на несколько частей, которые независимо хранятся доверенными участниками. Чтобы подвести итоги голосования, приватный ключ необходимо собрать и после этого расшифровать бюллетени. Если кто-то из доверенных участников «заболел», схема Шамира предполагает возможность сбора приватного ключа меньшим количеством участников. То есть если ключ был разбит на N частей, собрать обратно его можно, используя K частей, где K < N.
Такой вариант выглядит гораздо более надежным и продвинутым, и это действительно так. Но есть нюансы. Во-первых, в промежуток времени между генерацией ключа и его разделением он является очевидной мишенью для злоумышленников и единой точкой отказа системы. Во-вторых, после сбора ключа мы получаем возможность расшифровать каждый индивидуальный бюллетень. Это не позволит нам их отфильтровать, так как они уже находятся в блокчейне и никуда оттуда не денутся. Но это позволит нарушить конфиденциальность голосования. На бэкенде есть связка Ф.И. О. и публичного ключа участника голосования, а в блокчейне — связка публичного ключа и теперь уже расшифрованного бюллетеня. Мы знаем, как и кто проголосовал — можем взять и, например, лишить премии неугодных.
Конечно, существуют механизмы разрыва первой связки — персональных данных и открытого ключа — через технику слепой подписи, но это очень своеобразный механизм, который необходимо правильно внедрить. При этом всё равно может сохраниться возможность «вычислить по IP» голосующего. Он приходит на авторизованный метод получать слепую подпись, а потом стучится на неавторизованный метод отправить голос. Формально во втором случае мы не знаем, кто именно к нам пришел, и опираемся только на проверку слепой подписи. Но у нас есть возможность сопоставить параметры устройства/браузера/соединения и понять, что это тот самый Иванов, который 5 минут назад получал у нас слепую подпись. Или представим похожую атаку на сопоставление по времени получения подписи и отправки голоса. Когда голосующие идут толпой по 500 человек в секунду, такая атака теряет свою эффективность, но при меньшей нагрузке вполне себе работает.
Попробуем сделать лучше?
Распределенная генерация ключа
Попробуем и сделаем. В этом нам поможет протокол конфиденциального вычисления, позволяющий нескольким участникам произвести вычисление, зависящее от тайных входных данных каждого из них, таким образом, чтобы ни один участник не смог получить никакой информации о чужих тайных входных данных. Этот протокол обеспечивает процесс шифрования, в котором несколько сторон участвуют в вычислении общего открытого ключа голосования и соответствующего ему набора приватных ключей. При этом приватные ключи исходно создаются независимо, участники протокола конфиденциального вычисления не обмениваются ими — мы избавились от единой точки отказа. При этом мы имеем возможность реализовать пороговую схему K из N, аналогично схеме Шамира.
Для формирования общего открытого ключа голосования (MainPubliсKey) используется алгоритм DKG (distributed key generation) из статьи Torben Pryds Pedersen «A threshold cryptosystem without a trusted party», перенесенный на эллиптические кривые (в оригинальной статье используется мультипликативная группа конечного поля (поля Галуа) GF (p)). При этом есть ограничение: при любой жалобе (не сходится контрольная сумма) одного из участников на другого необходимо перезапустить процесс генерации с самого начала.
В нашей текущей реализации DKG используются стандартные эллиптические кривые seсp256k1 (Bitcoin, Ethereum) и функция хеширования SHA-256. Можно легко добавить, например, Ed25519 или даже российские кривые ТК-26 и хеш Стрибог, если потребуется. Также можно не завязываться на 256-битных кривых, а использовать 512-битные.
Участниками DKG у нас будут несколько экземпляров криптографических сервисов, выполняющих всю криптографическую магию. Чтобы не возникало вопросов о возможности «непрозрачного» общения между сервисами, единственным их интерфейсом будет взаимодействие с блокчейн-нодой. Один декрипт — одна нода. Принципиально такое соотношение 1 к 1 не требуется, декриптов может быть больше или меньше чем нод, но выглядит логичным иметь одинаковый уровень децентрализации как на слое хранения/транспорта данных (см. раздел выше), так и на слое криптографии.
Протокол создания открытого ключа мы будем запускать для каждого нового голосования, что позволит снизить ущерб для данных системы в случае компрометации одного из ключей.

Протокол DKG Pedersen 91 на эллиптических кривых
Параметры протокола:
Эллиптическая кривая E и генератор (Base) подгруппы этой кривой большого простого порядка q.
Другой генератор (BaseCommit) той же подгруппы, для которого число x из соотношения BaseCommit = x * Base неизвестно никому.
(k, n), где n — общее число развернутых криптографических сервисов (DecryptService), сгенерировавших пары ключей, а k — минимальное число сервисов, которое необходимо для восстановления общего секрета. k <= (n+1)/2, то есть если k — 1 участников — нечестные или у них украли ключи, то это никак не повлияет на безопасность общего секрета (MainPubliсKey).
Шаг 0. Индексы DecryptService
Каждому из n DecryptService присваивается уникальный порядковый номер от 1 до n. Это нужно, потому что от порядкового номера DecryptService зависит коэффициент Лагранжа, который потребуется для реализации схемы K из N.
Шаг 1. Создание открытого ключа голосования
Каждый из n DecryptService генерирует пару публичного (Pub_n) и приватного (priv_n) ключей для эллиптической кривой: j-й сервер генерирует пару ключей: priv_j, Pub_j, где Pub_j = priv_j * Base (точка Base — генератор простой подгруппы). И делает Pedersen commitment для публичного ключа:
Генерируется случайное число, скаляр r_j.
Вычисляется точка, коммит С_j = r * BaseCommit + Pub_j.
С_j публикуется в блокчейн.
После того как каждый из n DecryptService опубликовал свой коммит Педерсена С_j, каждый DecryptService публикует свой скаляр r_j. На основе опубликованных в блокчейне скаляров любой сторонний наблюдатель может восстановить публичные ключи каждого DecryptService — Pub_j = С_j — r * BaseCommit — а затем вычислить общий публичный ключ Pub (MainPublicKey) как сумму отдельных Pub_j.
Однако помимо открытого ключа голосования нам необходимо создать набор приватных ключей ему соответствующих, для расшифровывания итогов голосования. Для этого перейдем на…
Шаг 2. Генерация полиномов и раздача теней
Каждый j-й DecryptService случайным образом:
Генерирует полином степени k — 1: f_j (x) = f_j_0 + f_j_1*x + … + f_j_k-1* x^(k-1), где коэффициент f_j0 = priv_j, а остальные — случайные элементы поля GF (q), где q — порядок подгруппы точек.
Считает значения полинома для каждого i-го из n значений: f_j (i) = f_j_0 + f_j_1*i + … + f_j_k-1 * i^(k-1). Значение f_j (i) называется тенью (shadow).
Шифрует f_j (i) при помощи Pub_i для всех других серверов и публикует результаты шифрования. Таким образом, значение f_j (i) может узнать только владелец priv_i, т.е. DecryptService номер i.
Шаг 3. Проверка коэффициентов полиномов
Чтобы убедиться, что каждый из DecryptService следует протоколу DKG, они проверяют значения теней, полученных друг от друга. Каждый DecryptService публикует каждый коэффициент своего полинома, умноженного на генератор Base: j-й сервер: fj,0 * Base, fj,1 * Base, … , fj, k-1 * Base, где fj, k-1 — это коэффициент при степени k — 1.
После этого каждый i-й DecryptService проверяет все расшифрованные тени f_j (i) (где j из множества от 1 до n, исключая i), которые для него зашифровали другие n — 1 участников DKG. i-й DecryptService для тени от сервера j:
Вычисляет f_j (i) * Base
Берет экспоненты его коэффициентов: fj,0 * Base, fj.1 * Base, … , fj, k-1 * Base
Домножает каждый на соответствующую степень i: fj,0 * Base, i * (fj,1 * Base), … , i^(k-1) * (fj, k-1 * Base)
Складывает их.
Если результат сложения равен f_j (i) * Base (тень от j для i, умноженная на генератор), то результат принимается. В противном случае публикуется жалоба на сервер j: значение тени f_j (i), и протокол запускается с самого начала — шага 0.
Если ни у кого нет жалоб, то каждый сервер вычисляет свой секретный ключ s_i как сумму значений f_j (i) от всех j серверов, включая себя.
Если взять любые из k участников, то сложив их s_i * Lagrange (k, i), где Lagrange (k, i) — коэффициент Лагранжа, который зависит от номеров из выбранной группы (k) и номера i, мы получим приватный ключ, соответствующий общему ключу Pub (MainPublicKey), то есть по сути — сумму всех priv_i.
После того как мы выполнили шаг 3, мы можем быть уверены что у нас есть валидный общий открытый ключ голосования (MainPublicKey), а также набор соотвествующих ему приватных ключей, хранящихся на независимых криптографических сервисах. После этого мы можем опубликовать открытый ключ голосования в блокчейне и использовать его для шифрования бюллетеней.
Мы решили проблему «угона» приватного ключа до начала голосования. Он не был создан централизовано, и чтобы получить доступ к данным голосования, злоумышленнику необходимо «взломать» K серверов, а не один. Но остается вопрос: как мы будем проводить расшифровывание. Будем ли мы собирать приватный ключ в этот момент и дадим ли шанс злоумышленнику? Пожалуй, не дадим.
Шаг 4. Распределенное дешифрование
Допустим, мы зашифровываем сообщение M на открытом ключе голосования (MainPublicKey):
Генерируем число r и считаем R = r * Base.
Вычисляем С = M + r * MainPublicKey.
Получившийся шифротекст — пара точек (R, C) — мы публикуем в блокчейне.
Владелец приватного ключа priv вычисляет значение: priv * R.
И расшифровывает M: M = С — priv * R.
Таким образом, для расшифровывания (R, C) нужно вычислить priv * R.
Если наш приватный ключ распределен (допустим, что (k, n) = (3,6)), каждый криптографический сервис независимо считает значение s_i * R, используя свою часть приватного ключа, и публикует результат в блокчейне. Назовем это значение «частичной расшифровкой». Дальше остается домножить любые 3 из 6 результатов s_i * R на соответствующий коэффициент Лагранжа, сложить три точки и получить priv * R. А используя это значение, мы расшифровываем сообщение М.
Таким образом, мы получили возможность расшифровывать результаты голосования, не храня и не собирая приватный ключ в одном месте. Мы проводим распределенное дешифрование, когда каждый из DecryptService вычисляет результат «частичной расшифровки», публикует его, и на основании этих данных мы проводим итоговое дешифрование. При этом ни один из DecryptService не имеет возможности выполнить полное дешифрование единолично, а так как всё взаимодействие между криптографическими сервисами происходит в публичной области через блокчейн, мы всегда знаем, сколько раз выполнялись попытки дешифрования результатов.
Гомоморфное шифрование
Теперь у нас есть неплохой набор инструментов: мы защитили исторические данные (блокчейн), мы умеем создавать ключи шифрования и расшифрования без единой точки отказа (DKG), умеем пользоваться этими ключами прозрачным образом, также не имеющим единого слабого звена. Оба инструмента опираются на общую идеологию децентрализации, где мы не вынуждены доверять единому оператору системы, а можем положиться на нескольких независимых участников.
Но пока у нас не решен вопрос, что именно и каким образом мы будем шифровать. А также остается проблема нарушения конфиденциальности голосования, обозначенная выше, в случае расшифровывания индивидуальных бюллетеней.
На помощь нам приходит техника гомоморфного шифрования. Этот метод позволяет проводить арифметические операции над зашифрованными данными без их расшифровывания. То есть в системе, гомоморфной по сложению, мы можем сложить два зашифрованных числа, получить их зашифрованную сумму и расшифровать только результат сложения.

Использовать такую возможность в голосовании мы можем, представив бюллетень в виде матрицы, где каждая строка — это отдельный вопрос, по которому принимается решение, а ячейки в пределах строки — это варианты ответов на этот вопрос. Заполняя бюллетень, участник голосования выбирает вариант, и мы обозначаем его единицей. Остальные ячейки заполняются нулями. Затем мы шифруем каждую ячейку бюллетеня. Именно в таком зашифрованном виде бюллетень попадает в блокчейн. Что именно зашифровано в каждой ячейке — мы не знаем.
 Бюллетень в виде матрицы вопросов и вариантов ответов
Бюллетень в виде матрицы вопросов и вариантов ответовНо, благодаря гомоморфному шифрованию, мы имеем возможность отдельно по каждому вопросу провести «сложение столбиком» всех полученных бюллетеней. После чего мы можем расшифровать уже только итоги голосования, без расшифровывания индивидуальных бюллетеней.
 Подсчет результатов в зашифрованном виде
Подсчет результатов в зашифрованном видеВ итоге мы получаем не только совместную и прозрачную работу нескольких независимых сервисов при вычислении итогов голосования, где ни один из них не может эти результаты подтасовать. Мы также добились очень высокого уровня конфиденциальности голосования. Мы анонимизировали выбор участников голосования через «сложение столбиком» — у нас есть сумма, но нам неизвестны слагаемые!
Чтобы добиться этого, мы используем криптосистему Эль-Гамаля. Исходно эта криптосистема опирается на задачу дискретного логарифма на конечном поле и является гомоморфной к умножению, но она может быть модифицирована для работы на эллиптических кривых и приведена к гомоморфизму по сложению. В разделе выше показано, как выглядит зашифрованное сообщение:
Зашифрованное сообщение 1: (R1, С1) =(r1 * Base, M1 + r1 * MainPublicKey )
Зашифрованное сообщение 2: (R2, С2) =(r2 * Base, M2 + r2 * MainPublicKey )
Их сумма: (R1 + R2, C1 + C2) = ((r1+r2) * Base, M1 + M2 + (r1 + r2) * MainPublicKey )
Сумму расшифровываем так же, как отдельные сообщения (помним что MainPublicKey = priv * Base):
(M1 + M2) = (C1 + C2) — priv * (R1 + R2) = M1 + M2 + (r1 + r2) * MainPublicKey — priv * (r1 + r2) * Base = M1 + M2
Кто-то скажет «магия», кто-то возразит — «математика».
В результате мы, кажется, сделали все возможное, чтобы защитить участника голосования. Его голос нельзя подделать, его нельзя прочитать, его практически нельзя заблокировать или «потерять». Участника голосования нельзя лишить премии за выбор «неправильного» кандидата.
Более того, мы можем предложить решение для проблемы, характерной для всех систем голосования, где участник отправляет заполненный бюллетень не в защищенном и изолированном пространстве избирательной кабины, а в произвольном месте и в непредсказуемом окружении — проблемы принуждения к голосованию. То есть когда на голосующего, в момент отправки голоса оказывается давление выбрать конкретного кандидата. Так как голос, отправленный под давлением, считается технически валидным, система примет его как голос, отправленный от имени публичного ключа пользователя. Но ничего не мешает голосующему отправить свой голос несколько раз. Каждый отправленный бюллетень будет зарегистрирован в системе, но при подсчете итогов мы посчитаем только последний из бюллетеней, отправленных от имени публичного ключа участника голосования.
Доказательства с нулевым разглашением (ZKP — Zero Knowledge Proofs)
Однако не только организатор или внешний злоумышленник могут иметь мотивацию повлиять на исход выборов. Нарушитель может затесаться и в ряды участников голосования. Поскольку мы используем очень простую механику «сложения столбиком» и не заглядываем в индивидуальные бюллетени, у участника голосования есть возможность покопаться в клиентском приложении и сформировать бюллетень, где он вместо »1» проставит за своего кандидата значение »100500». Или »–100500» за того, кого недолюбливает. Система посчитает итоги, и кандидат нарушителя победит с «внушительным преимуществом».
Чтобы исключить такую возможность, мы используем еще одну крипто-магическую технику — доказательства с нулевым разглашением. Эта механика позволяет доказать обладание какой-либо информацией без ее раскрытия или доказать, что вы зашифровали корректное значение (например, находящееся в допустимых пределах) не раскрывая самого значения.
Одна из самых наглядных демонстраций работы ZKP (интерактивной разновидности) — это «Пещера Али-Бабы» или «Лабиринт»:
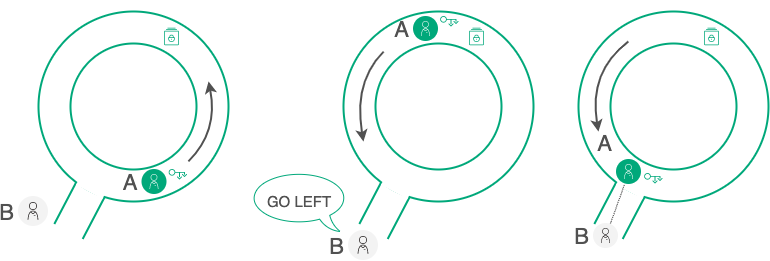
Участник «A» обладает ключом, открывающим дверь в лабиринте, и хочет доказать это участнику «B», но не хочет показывать ключ. Чтобы «В» мог убедиться в верности утверждения «А», они организуют серию испытаний:
«А» заходит в лабиринт пока «В» отвернулся. «В» не знает, в какую сторону пошел «А».
«В» дает «А» указание выйти с какой-либо стороны, например, слева.
Если «А» действительно обладает ключом, он может появиться с любой стороны и выполняет указание «В».
Шанс того, что «А» просто повезло, и он, не имея ключа, изначально пошел налево, составляет 50/50. Поэтому они повторяют испытание еще и еще раз, пока вероятность «везения» не станет пренебрежимо малой, и «В» не признает, что «А» действительно обладает ключом. При этом «В» не увидит самого ключа, не получит никакой информации, которой обладает А (направление, которое «А» выбирает в каждом испытании), но в результате серии испытаний он получит достоверное (вероятностное, но с любой необходимой «В» точностью) доказательство.
Неинтерактивные доказательства с нулевым разглашением позволяют упростить взаимодействие между сторонами, и именно их мы будем использовать. Для защиты от нечестного участника голосования мы применим следующую схему доказательств:
ZKP на бюллетене
По каждому вопросу мы, помимо заполненных и зашифрованных ячеек с вариантами выбора, к каждой ячейке приложим NIZK, доказывающее, что в этой ячейке зашифровано одно из значений — »0» или »1» —, но не раскрывающее, какое именно. И дополнительно приложим доказательство, что зашифрованная сумма значений всех ячеек по вопросу равна »1». Это означает, что участник голосования может поставить »1» в любую из ячеек и выбрать только один вариант.

При желании (а оно у нас есть) мы можем на базе этой схемы ZKP реализовать более сложные схемы голосований. Например, взвешенное голосование, где каждый участник отдает не один голос, а количество голосов, пропорциональное своей доле акций компании. Для этого мы должны вместо »1» создать ZKP для значения веса голоса участника. Или вариант голосования с множес
