Быстрее, чем C++; медленнее, чем PHP
Привет, Хабр.
У меня тут случайно код на хаскеле получился быстрее аналогичного кода на C++. Иногда — на 40%.
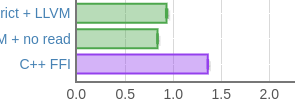
(время работы, меньше — лучше, C++ снизу)
Что самое смешное — я собирал хаскель-код через LLVM-бекенд, но при этом сравнивал с GCC. Если сравнивать с clang (что вроде как логичнее), то всё становится ещё хуже для плюсов: почему-то на этой задаче clang проигрывает GCC в пару раз, и разница становится не 40%, а этак раза три. Впрочем, одна маленькая модификация C++-кода это поменяет.
Началось всё с того, что для одного моего проекта (который, естественно, делается на хаскеле, и о котором я тоже скоро напишу) нужно было быстро и эффективно считать расстояние Левенштейна между двумя строками. Расстояние Левенштейна — это такая метрика, которая говорит, сколько символов нужно удалить, добавить или заменить в одной строке, чтобы она стала равна другой строке. Я считал расстояния между довольно большими строками (масштаба десятков тысяч символов), поэтому эффективность была действительно важна.
А потом мне стало интересно, насколько быстро я вообще могу это расстояние считать (потратив разумное время на оптимизацию, конечно), так что я набросал вариант на С++ и взял его время работы за этакий идеал, к которому стоит стремиться. Впрочем, как уже понятно, идеал оказался превзойдён.
Посмотрим, как этого можно достичь?

В качестве бонуса — сравнение с некоторыми другими языками. Спойлеры:
- Nim медленнее компилятора C двадцатилетней давности.
- C# в пять раз медленнее Java, которая оказывается вполне на уровне Rust.
- Go вровень с C.
- PHP быстрее питона (что оправдывает вторую часть заголовка).
Нахождение расстояния Левенштейна — как раз одна из тех задач, что просто создана для динамического программирования. Классическое решение сводится к построению матрицы размера (где
и
— длины строк) и построчному её заполнению сверху вниз. Увы, если строки имеют смешной размер порядка десятка килобайт, то такая матрица сожрёт 0.5–1 гигабайт, что не очень приятно. Однако, если присмотреться, то можно заметить, что мы в каждый момент времени используем только две строки (текущую заполняемую и предыдущую), поэтому можно хранить только их.
На самом деле можно обойтись одной строкой, но нам и с двумя хорошо будет.
Будем замерять производительность двумя способами.
Во-первых, есть замечательный пакет criterion, который помогает делать бенчмарки правильно, запуская код много раз, высчитывая всякие стандартные отклонения и прочие статистики.
Но запускать его долго, поэтому у нас будет ещё один наколенный бенчмарк. Возьмём три строки s1, s2, s3, первые две из которых состоят из 20000 символов 'a', а последняя — из 20000 символов 'b', и будем считать расстояния от s1 до s2 и от s1 до s3 (естественно, ожидая получить 0 и 20000).
Так как выделение полсотни килобайт и заполнение их одним и тем же символом — ничто по сравнению со временем работы алгоритма, мы просто будем замерять время работы всей программы (в случае хаскеля — согласно +RTS -sstderr). Чтобы не делать бенчмарк совсем уж наколенным, защитимся от выбросов: будем запускать код три раза и брать минимум из трёх. Минимум, а не среднее — так как случайная активность на машине может заставить код выполняться медленнее, чем он есть на самом деле, а вот быстрее выполнять не получится. Тем более, что никакой случайности во входных данных у нас нет, и выполнение строго детерминированно.
По ходу рассмотрения различных вариантов кода мы будем рассматривать лишь результаты этого наколенного бенчмарка, а аккуратные графики criterion’а будут в самом конце.
Давайте начнём с ожиданий: насколько быстро мы можем решить нашу задачу в этих условиях? Это можно оценить двумя способами: очень грубо теоретически и чуть более аккуратно практически.
Предположим, что все наши данные помещаются в L2-кеш, но из L1 они таки вымываются. Обосновано ли это предположение? Посмотрим, что нам нужно хранить:
- Две строки по 20000 байт: примерно 40 килобайт (это уже больше, чем L1 на моей машине!).
- Два массива по 20000 8-байтных чисел, что даёт нам дважды по 160 — итого 320 килобайт (и даже если бы мы использовали 4-байтные инты, то это бы всё равно было 160 килобайт, что куда больше L1).
Сколько данных за время работы алгоритма мы должны передать в/из L2?
Мы сделаем в районе 20000 итераций, каждая из которых читает одну из строк целиком (20 КБ), весь построенный на прошлом шаге массив (160 КБ), и при этом пишет новую строку (ещё 160 КБ). Оптимистично предполагая, что запись ни на что не влияет (у нас же грубая оценка снизу) рассмотрим только чтение: суммарно нам нужно прочитать (20 + 160)×20000 КБ из L2, что равно 3.6 ГБ. Учитывая, что, судя по разным источникам, мой Haswell имеет устоявшуюся скорость чтения из L2 в районе 50 ГБ/с, это даст нам порядка 0.1 с на одну пару строк, или 0.2 с на весь тест. Быстрее мы никак не можем.
Ну, то есть, совсем теоретически могли бы, но решение этой задачи блочным образом, чтобы помещаться в L1, совсем не подняло производительность.
Набросаем вот эту программу на C++:
#include
#include
#include
#include
#include
size_t lev_dist(const std::string& s1, const std::string& s2)
{
const auto m = s1.size();
const auto n = s2.size();
std::vector v0;
v0.resize(n + 1);
std::iota(v0.begin(), v0.end(), 0);
auto v1 = v0;
for (size_t i = 0; i < m; ++i)
{
v1[0] = i + 1;
for (size_t j = 0; j < n; ++j)
{
auto delCost = v0[j + 1] + 1;
auto insCost = v1[j] + 1;
auto substCost = s1[i] == s2[j] ? v0[j] : (v0[j] + 1);
v1[j + 1] = std::min({ delCost, insCost, substCost });
}
std::swap(v0, v1);
}
return v0[n];
}
int main()
{
std::string s1(20000, 'a');
std::string s2(20000, 'a');
std::string s3(20000, 'b');
std::cout << lev_dist(s1, s2) << std::endl;
std::cout << lev_dist(s1, s3) << std::endl;
} Минимум времени работы этой программы из трёх запусков — 1.356 секунд (Core i7 4770, никакого оверклокинга). При этом использовался gcc 9.2, опции — -O3 -march=native.
Как уже упоминалось во введении, clang (9.0.1, естественно, с теми же опциями) показывает себя хуже: время работы оказывается в районе 2.6–2.7 с.
Так что наша цель — 1.3 секунды.
Наивная чистая реализация
Никакой явной мутабельности (кроме того, что внутри Data.Vector, но это не наша кухня), никакой явной хвостовой рекурсии. Просто строгая левая свёртка и немного костыльный Data.Vector.constructN:
import qualified Data.ByteString as BS
import qualified Data.Vector.Unboxed as V
import Data.List
levenshteinDistance :: BS.ByteString -> BS.ByteString -> Int
levenshteinDistance s1 s2 = foldl' outer (V.generate (n + 1) id) [0 .. m - 1] V.! n
where
m = BS.length s1
n = BS.length s2
outer v0 i = V.constructN (n + 1) ctr
where
s1char = s1 `BS.index` i
ctr v1 | V.length v1 == 0 = i + 1
ctr v1 = min (substCost + substCostBase) $ 1 + min delCost insCost
where
j = V.length v1
delCost = v0 V.! j
insCost = v1 V.! (j - 1)
substCostBase = v0 V.! (j - 1)
substCost = if s1char == s2 `BS.index` (j - 1) then 0 else 1Это может показаться немного уродливым, но, на мой взгляд, это всё равно достаточно читабельный и идиоматичный код (насколько такие алгоритмы вообще могут быть идиоматично представимыми).
Время согласно наколенному бенчмарку? 5.5 секунд. Как-то не оч.
Можно ли лучше?
Тривиальные улучшения
К счастью, есть пара способов улучшить производительность, вообще не трогая код.
Во-первых, вряд ли компилятор правильно вывел все характеристики строгости. Давайте ему поможем и добавим {-# LANGUAGE Strict #-} в самое начало файла. Конечно, мы могли бы быть более дотошными и начать аккуратно расставлять bang patterns, но и так сойдёт.
В любом случае, это уменьшает время работы до 3.4 секунд. Куда лучше, но всё ещё так себе.
Во-вторых, давайте вдобавок попробуем использовать не штатный кодогенератор GHC (NCG — Native CodeGen), а LLVM? Для этого добавим {-# OPTIONS_GHC -fllvm #-} в начало файла. Результат? 2.1 секунд. Это уже что-то! И, кстати, уже даже этот вариант быстрее того, что сгенерировал clang.
Чистая реализация с небезопасными операциями
Теперь попробуем чуть более значимые улучшения: заменим операции доступа по индексу их небезопасными версиями (которые, впрочем, эквивалентны по безопасности плюсовым operator[]). Так V.! заменяется на V.unsafeIndex, а BS.index на BS.unsafeIndex.
import qualified Data.ByteString as BS
import qualified Data.ByteString.Unsafe as BS
import qualified Data.Vector.Unboxed as V
import Data.List
levenshteinDistance :: BS.ByteString -> BS.ByteString -> Int
levenshteinDistance s1 s2 = foldl' outer (V.generate (n + 1) id) [0 .. m - 1] V.! n
where
m = BS.length s1
n = BS.length s2
outer v0 i = V.constructN (n + 1) ctr
where
s1char = s1 `BS.unsafeIndex` i
ctr v1 | V.length v1 == 0 = i + 1
ctr v1 = min (substCost + substCostBase) $ 1 + min delCost insCost
where
j = V.length v1
delCost = v0 `V.unsafeIndex` j
insCost = v1 `V.unsafeIndex` (j - 1)
substCostBase = v0 `V.unsafeIndex` (j - 1)
substCost = if s1char == s2 `BS.unsafeIndex` (j - 1) then 0 else 1Интересно, что в идеальном мире хаскеля с зависимыми типами нам бы не потребовалось делать эту замену: мы могли бы статически доказать безопасность всех индексов, тем самым избавившись от рантайм-проверок и при этом сохранив безопасность.
В любом случае, время выполнения (без всех тривиальных улучшений) составляет 4.2 секунды (против 5.5 секунд «безопасной» версии).
А что с улучшениями?
Добавление {-# LANGUAGE Strict #-} сокращает время до 2.5 секунд (против 3.4 секунд «безопасной» версии).
Компиляция через LLVM улучшает результат аж до 1.6 секунд (против 2.1 секунд ранее). Это уже быстрее clang!
И вообще, это интересный результат по ряду причин:
- Мы уже получили почти-C++-производительность, в то же время по-прежнему имея достаточно идиоматичный код.
- Мы получаем такие результаты несмотря на то, что мы аллоцируем новый массив на каждой итерации (то есть, в 20000 раз больше, чем это делает C++-версия). К счастью, каждый такой массив не очень долгоживущий, так что он умирает и собирается GC ещё в роддоме нулевом поколении. Сборщики мусора с поколениями рулят и педалят!
- «Штраф за безопасность» что строгой, что нестрогой версии составляет примерно 20% при использовании NCG. Лично я бы ожидал существенно меньшее влияние проверок на производительность — они никогда не срабатывают, так что предсказатель ветвлений должен достаточно быстро понять соответствующий паттерн.
- Использование LLVM-бекенда уменьшает этот штраф до примерно 0.5 секунд. Почему? LLVM способен избавиться от некоторых проверок, или же сами проверки становятся более дружественными к предсказателю ветвлений? Или оба фактора сразу?
Реализация с мутабельностью
Давайте начнём с прямого переписывания алгоритма с использованием мутабельного Data.Array.ST:
import qualified Data.Array.Base as A(unsafeRead, unsafeWrite)
import qualified Data.Array.ST as A
import qualified Data.ByteString.Char8 as BS
import Control.Monad
import Control.Monad.ST
levenshteinDistance :: BS.ByteString -> BS.ByteString -> Int
levenshteinDistance s1 s2 = runST $ do
v0Init <- A.newListArray (0, n) [0..]
v1Init <- A.newArray_ (0, n)
forM_ [0 .. m - 1] $ \i -> do
let (v0, v1) | even i = (v0Init, v1Init)
| otherwise = (v1Init, v0Init)
loop i v0 v1
A.unsafeRead (if even m then v0Init else v1Init) n
where
m = BS.length s1
n = BS.length s2
loop :: Int -> A.STUArray s Int Int -> A.STUArray s Int Int -> ST s ()
loop i v0 v1 = do
A.unsafeWrite v1 0 (i + 1)
let s1char = s1 `BS.index` i
forM_ [0..n - 1] $ \j -> do
delCost <- v0 `A.unsafeRead` (j + 1)
insCost <- v1 `A.unsafeRead` j
substCostBase <- v0 `A.unsafeRead` j
let substCost = if s1char == s2 `BS.index` j then 0 else 1
A.unsafeWrite v1 (j + 1) $ min (substCost + substCostBase) $ 1 + min delCost insCostПо моему опыту массивы (в смысле Data.Array.ST) оказываются быстрее векторов (Data.Vector.Mutable и их unboxed-версия) при некоторых дополнительных условиях, которые здесь выполняются. Поэтому (а также в целях удержания размера поста в рамках разумного) рассматривать версию на векторах мы не будем. Ровно по тем же причинам мы не будем рассматривать «безопасные» функции для индексации и сразу обратимся к unsafeRead/unsafeWrite.
Насколько быстро работает этот вариант?
5.9 секунд. Чёрт. Куда хуже, чем безопасная и чистая реализация! И даже если мы отпрофилируем этот код, то окажется, что… В общем, ничего интересного из этого профиля не выйдет.
С другой стороны, эта реализация по крайней мере почти не требует GC: 2–3 минорных сборки мусора и 2–3 мажорных (согласно +RTS -sstderr) против тысяч минорных в случае чистого Data.Vector. Впрочем, как мы видим, даже это не особо помогает производительности — GC с поколениями рулят, живи быстро, умри молодым.
Как насчёт наших старых добрых друзей?
Строгость уменьшает время работы до 4.1 секунды. Сборка через LLVM выигрывает ещё 0.4 секунды, позволяя достичь суммарного времени в 3.7 секунд.
Нет, спасибо, я лучше останусь с чистой версией.
Но давайте продолжим.
Явная хвостовая рекурсия
Есть множество свидетельств того, что GHC очень любит хвостовую рекурсию, так что давайте перепишем наш код так, чтобы она была явной. Для этого придётся убрать комбинатор forM_ и получить примерно следующий код:
import qualified Data.Array.Base as A(unsafeRead, unsafeWrite)
import qualified Data.Array.ST as A
import qualified Data.ByteString.Char8 as BS
import Control.Monad.ST
levenshteinDistance :: BS.ByteString -> BS.ByteString -> Int
levenshteinDistance s1 s2 = runST $ do
v0Init <- A.newListArray (0, n) [0..]
v1Init <- A.newArray_ (0, n)
loop 0 v0Init v1Init
A.unsafeRead (if even m then v0Init else v1Init) n
where
m = BS.length s1
n = BS.length s2
loop :: Int -> A.STUArray s Int Int -> A.STUArray s Int Int -> ST s ()
loop i v0 v1 | i == m = pure ()
| otherwise = do
A.unsafeWrite v1 0 (i + 1)
let s1char = s1 `BS.index` i
let go j | j == n = pure ()
| otherwise = do
delCost <- v0 `A.unsafeRead` (j + 1)
insCost <- v1 `A.unsafeRead` j
substCostBase <- v0 `A.unsafeRead` j
let substCost = if s1char == s2 `BS.index` j then 0 else 1
A.unsafeWrite v1 (j + 1) $ min (substCost + substCostBase) $ 1 + min delCost insCost
go (j + 1)
go 0
loop (i + 1) v1 v0Время работы этого варианта — 4.3 секунды. Строгость снижает время работы до 1.7 секунд — прямо как с векторами с небезопасной индексацией. Если честно, я удивлён и обескуражен тем, что GHC не смог оптимизировать forM_ так же хорошо, как он смог это сделать с хвостовой рекурсией.
Но теперь давайте попробуем собрать с LLVM.
0.96 секунд. Шта? Быстрее чем C++? Я где-то сделал ошибку?

0.96 секунд.
Но можно лучше.
Всякая мелочь
Мы всё ещё безопасно читаем строки (на самом деле я просто забыл это поправить при написании начальной мутабельной версии, а потом было лень переделывать бенчмарки).
Замена BS.index на BS.unsafeIndex срезает ещё 0.04 секунды, давая время работы в 0.92 секунды.
Кроме того, есть ещё одна оптимизация, которую можно попробовать. Заметим, что мы пишем в v1[j+1] на j-ой итерации и читаем из того же элемента на следующей итерации. Что будет, если мы будем явно передавать соответствующее значение в рекурсивный вызов?
{-# LANGUAGE Strict #-}
{-# OPTIONS_GHC -fllvm #-}
import qualified Data.Array.Base as A(unsafeRead, unsafeWrite)
import qualified Data.Array.ST as A
import qualified Data.ByteString as BS
import qualified Data.ByteString.Unsafe as BS
import Control.Monad.ST
levenshteinDistance :: BS.ByteString -> BS.ByteString -> Int
levenshteinDistance s1 s2 = runST $ do
v0Init <- A.newListArray (0, n) [0..]
v1Init <- A.newArray_ (0, n)
loop 0 v0Init v1Init
A.unsafeRead (if even m then v0Init else v1Init) n
where
m = BS.length s1
n = BS.length s2
loop :: Int -> A.STUArray s Int Int -> A.STUArray s Int Int -> ST s ()
loop i v0 v1 | i == m = pure ()
| otherwise = do
A.unsafeWrite v1 0 (i + 1)
let s1char = s1 `BS.unsafeIndex` i
let go j prev | j == n = pure ()
| otherwise = do
delCost <- v0 `A.unsafeRead` (j + 1)
substCostBase <- v0 `A.unsafeRead` j
let substCost = if s1char == s2 `BS.unsafeIndex` j then 0 else 1
let res = min (substCost + substCostBase) $ 1 + min delCost prev
A.unsafeWrite v1 (j + 1) res
go (j + 1) res
go 0 (i + 1)
loop (i + 1) v1 v0Эта микрооптимизация даёт нам примрено 0.09 секунд, уменьшая время работы до 0.83 секунд. Это победа.
Интересно, что аналог этой микрооптимизации для C++ ни на что не влияет.
Я думаю, что это уже вполне неплохо (и на самом деле не так уж ужасно выглядит, тем более, что на всё я потратил не больше часа). Давайте перейдём к итоговым результатам и графикам.
Наколенные бенчмарки
Сначала сведем результаты всех наколенных бенчмарков в одну таблицу. Базовое время для C++-версии — 1.36 секунд, все остальные времена отнормированы относительно него (так что оно составляет 100%).
У меня также была возможность прогнать некоторые из тестов на машине с i7–6700, и две наиболее важные точки таковы:
- 178% для чистой версии с небезопасной индексацией,
- 84% для наиболее эффективной версии.
Похоже, что Haskell ближе к Haswell, чем к Skylake. Хотя, конечно, даже на последнем наибыстрейшая Haskell-версия быстрее C++.
Результаты criterion
Приведём скриншоты графиков criterion (увы, JavaScript тут вставлять нельзя, так что они неживые).
На Haswell (i7 4770):
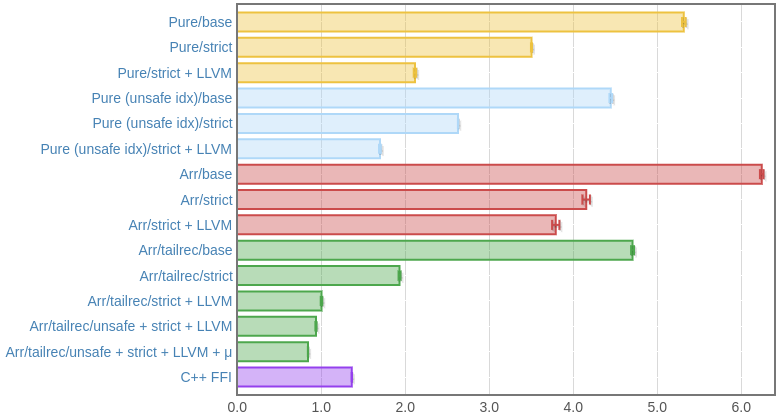
На Skylake (i7 6700):

Здесь использовалась C++-версия, которая вызывается через FFI. Однако время работы получилось плюс-минус равным времени «чистой» C++-версии без всякого FFI, что позволяет считать, что расходами на FFI можно пренебречь (да и этого следовало бы ожидать исходя из того, как в памяти представляются ByteString).
- На чистом, достаточно идиоматичном хаскеле вполне возможно достичь не настолько уж далеко отстоящей от C++ производительности.
- Строгость (вернее, её корректное использование) важна.
- Хвостовая рекурсия важна. GHC, увы, не способен заметить, что некоторые вещи могут быть выражены через хвостовую рекурсию, и приходится объяснять ему это вручную. Так что при написании вычислительно тяжёлых алгоритмов точно стоит уделить этому внимание.
- LLVM важен. Я нечасто видел, чтобы использование LLVM давало такой профит даже в некоторых числодробильных алгоритмах, так что приятно видеть задачу, где от этого есть прок.
- Оптимизация кода — строго нелинейный процесс. Нельзя ожидать, что одно и то же изменение (даже очень «техническое» вроде строгости или изменения бекенда) даст одинаковый прирост производительности для различных формулировок даже одного и того же алгоритма.
В частности, был соблазн даже не рассматриватьData.Array.STпосле того, как мы увидели, как плохо он себя показывает по сравнению с чистой версией, но именно он оказался победителем.
О чём я умолчал в посте?
- В первую очередь, на некотором мета-уровне рассуждений, это история успеха. Этот пост не означает, что хаскель всегда может быть оптимизирован так, чтобы соответствовать C++-версии. Мне просто в известном смысле повезло натолкнуться на задачу, где это действительно так. Окажись это не совсем так, этот пост не был бы таким радостным (или вообще не был бы).
- Импорт правильных строк важен.
Data.ByteString.Char8ненамного, но статистически значимо медленнее, чемData.ByteString. - Версия GHC важна. Исследование этого, впрочем, составляет ещё одно измерение в пространстве этого бенчмарка.
Код в этом посте компилировался при помощи GHC 8.6 (Stackage LTS 14.16). GHC 8.8 (с одним из nightly-снапшотов Stackage), похоже, генерирует более эффективный код при компиляции с NCG, но в среднем проигрывает при использовании LLVM. Однако, это не влияет на наиболее быстрый из представленных вариантов. - Зависимые типы, блин, важны. На самом деле в посте я это уже упомянул, но не могу не подчеркнуть это ещё раз. Необходимость писать
unsafeтам, где в более выразительном языке вполне всё можно доказать статически и избавиться от рантайм-проверок, не потеряв в безопасности — это ужасно, это как лопата дворника по асфальту зимой. - Ещё один аспект, который было бы интересно исследовать — поведение на более широком наборе входов. Несмотря на то, что количество итераций алгоритма не зависит от входных данных, вряд ли сравнение двух одинаковых (или двух полностью разных) строк представляет репрезентативный бенчмарк.
- Микроархитектура важна. Необходимо отметить, что, помимо упомянутой разницы между Haswell и Skylake, я также получил репорт о том, что C++-код и хаскель-код идут вровень на некоторых машинах. У меня это воспроизвести не получилось, и тот репорт был от обладателя Ryzen, так что я виню AMD.
Ну и даже одинаковая производительность — это всё равно круто. - Наверняка наша базовая C++-версия может быть ещё более оптимизирована, но я не хочу тратить на это больше времени, чем я потратил на оптимизацию хаскель-версии (иначе теряется всякий смысл — и на хаскеле можно генерировать LLVM IR, например).
- Кроме того, я получил репорт о том, что замена
std::minна вручную написанное сравнение улучшает производительность. Мне это удалось воспроизвести, но с двоякими результатами: gcc замедляется ещё больше, до 1.4–1.5 секунд, а clang резко ускоряется — до примерно 0.84 с, что вполне на уровне GHC.
Впрочем, разворачиваниеstd::minускоряет и хаскель-версию, и это не та оптимизация, которая имеет смысл в контексте поста. - И, наконец, входные строки важны. Я сделал пару ещё более наколенных тестов на случайных строках, и что хаскель-, что C++-версия немного замедлились. Но аккуратно бенчмаркать со случайными данными, да ещё между двумя разными языками, да с прицелом на портирование на ещё пару дюжин языков (см. ниже) сложно, да и смысл поста не в этом.
Так что воспринимайте этот пост с долей скептицизма.
А теперь начнём специальную олимпиаду и посмотрим, как другие языки справятся с этой задачей. Методика сравнения та же — запускаем трижды, берём минимальное значение.
Скажу сразу — я ни на одном из них писать не умею (кроме C++), так что ничего про них сказать не могу. С этими всеми реализациями мне помог XRevan86 — чувак настоящий полиглот и фанат своего дела, так что подписывайтесь, ставьте лайк.
Код для всех примеров сравнивает строки длиной 15 тысяч символов, а не 20, однако числа перенормированы для длины в 20 тысяч символов.
Мы отдельно рассмотрим компилируемые языки (куда мы также для простоты и холивара включим Java и C#) и отдельно — интерпретируемые.
Компилируемые языки
C++-вариант приведен для сравнения. Его можно оптимизировать ещё немного (например, развернув руками std::min или заменив std::vector/std::string на сырые данные), но тогда это получится C с плюсовым main’ом, что не так интересно. Если бы я писал научную работу, я бы написал «out of scope of this work».
С-вариант с технологиями 2000-ого года (BCC 5.5) приведен для лулзов. Другие варианты приведены для демонстрации зависимости от компилятора и его опций.
Наблюдения:
- nim’у пока не удалось победить Borland C++ Compiler, выпущенный в 2000-м году. Увы.
- Разница между Java и C# какая-то огромная, и Java оказывается подозрительно близко к вершине, хотя я просто сделал
javac -g:none LevDist.java && java LevDist. Наверное, тут что-то совсем не так. Хотя, с другой стороны, это очень JIT-friendly-задача, так что, может, здесь JIT творит чудеса. - Ещё любопытно, что clang умудряется подчистую сливать на C++-коде, но при этом вырываться вперёд на С-коде.
- C# с .NET Core у меня не получилось запустить, и я взял результаты XRevan86, отнормировав их на разницу производительностей наших машин согласно остальным результатам. Научность зашкаливает, понимаю.
- Везде куча ансейфа. Интересно, насколько он влияет в разных языках?
- В некоторых реализациях (по крайней мере, в С++) время работы зависит от порядка сравнений. Оптимизировать этот порядок — имхо скорее читерство и снова out of scope.
- При некоторых из этих порядков мне таки удалось воспроизвести ускорение в случае C++. Так, если вместо
std::min({ delCost, insCost, substCost })написатьstd::min(substCost, std::min(delCost, insCost)), то время работы под gcc увеличивается до 1.440 секунд, а под clang — уменьшается до 0.840 секунд (ура, быстрее всех остальных вариантов и почти хаскель). Похоже, clang не любит initializer lists и не может их заинлайнить, а gcc шедулит операции и регистры так, что, по крайней мере, на этих конкретных данных результат проигрывает.
Но ещё раз отмечу, что оптимизацией порядка в случае хаскеля я не занимался, и заниматься этим в рамках этого бенчмарка не рекомендую в любом языке.
Кроме того, это значит, что нельзя рассчитывать на компилятор даже в таком языке, как C++, где в компиляторы влиты десятки тысяч человеколет.
Собственно код выглядит так:
#include
#include
#include
#include
static long
lev_dist (const char *s1,
const char *s2)
{
unsigned long m, n;
unsigned long i, j;
long *v0, *v1;
long ret, *temp;
m = strlen (s1);
n = strlen (s2);
/* Edge cases. */
if (m == 0) {
return n;
} else if (n == 0) {
return m;
}
v0 = malloc (sizeof (long) * (n + 1));
v1 = malloc (sizeof (long) * (n + 1));
if (v0 == NULL || v1 == NULL) {
fprintf (stderr, "failed to allocate memory\n");
exit (-1);
}
for (i = 0; i <= n; ++i) {
v0[i] = i;
}
memcpy (v1, v0, n + 1);
for (i = 0; i < m; ++i) {
v1[0] = i + 1;
for (j = 0; j < n; ++j) {
const long subst_cost = (s1[i] == s2[j]) ? v0[j] : (v0[j] + 1);
const long del_cost = v0[j + 1] + 1;
const long ins_cost = v1[j] + 1;
#if !defined(__GNUC__) || defined(__llvm__)
if (subst_cost < del_cost) {
v1[j + 1] = subst_cost;
} else {
v1[j + 1] = del_cost;
}
#else
v1[j + 1] = (subst_cost < del_cost) ? subst_cost : del_cost;
#endif
if (ins_cost < v1[j + 1]) {
v1[j + 1] = ins_cost;
}
}
temp = v0;
v0 = v1;
v1 = temp;
}
ret = v0[n];
free (v0);
free (v1);
return ret;
}
int
main ()
{
const int len = 15000;
int i;
char s1[15001], *s2 = s1, s3[15001];
clock_t start_time, exec_time;
for (i = 0; i < len; ++i) {
s1[i] = 'a';
s3[i] = 'b';
}
s1[len] = s3[len] = '\0';
start_time = clock ();
printf ("%ld\n", lev_dist (s1, s2));
printf ("%ld\n", lev_dist (s1, s3));
exec_time = clock () - start_time;
fprintf (stderr,
"Finished in %.3fs\n",
((double) exec_time) / CLOCKS_PER_SEC);
return 0;
}
def lev_dist(s1 : String, s2 : String) : Int
m = s1.bytesize
n = s2.bytesize
# Edge cases.
return n if m == 0
return m if n == 0
v0 = (Slice.new(n + 1) { |i| i }).to_unsafe
v1 = (Slice.new(n + 1) { |i| i }).to_unsafe
ca1, ca2 = s1.bytes, s2.bytes
ca1.each_with_index do |c1, i|
v1[0] = i + 1
ca2.each_with_index do |c2, j|
subst_cost = (c1 == c2) ? v0[j] : (v0[j] + 1)
del_cost = v0[j + 1] + 1
ins_cost = v1[j] + 1
# [del_cost, ins_cost, subst_cost].min is slow.
min_cost = (subst_cost < del_cost) ? subst_cost : del_cost
if ins_cost < min_cost
min_cost = ins_cost
end
v1[j + 1] = min_cost
end
v0, v1 = v1, v0
end
return v0[n]
end
s1 = "a" * 15_000
s2 = s1
s3 = "b" * 15_000
exec_time = -Time.monotonic.to_f
puts lev_dist(s1, s2)
puts lev_dist(s1, s3)
exec_time += Time.monotonic.to_f
STDERR.puts "Finished in #{"%.3f" % exec_time}s"using System;
using System.Diagnostics;
using System.Linq;
using System.Text;
public class Program
{
public static Int32 LevDist(string s1, string s2)
{
var ca1 = Encoding.UTF8.GetBytes(s1);
var ca2 = Encoding.UTF8.GetBytes(s2);
return LevDist(ca1, ca2);
}
public static Int32 LevDist(byte[] s1, byte[] s2)
{
var m = s1.Length;
var n = s2.Length;
// Edge cases.
if (m == 0)
{
return n;
}
else if (n == 0)
{
return m;
}
Int32[] v0 = Enumerable.Range(0, n + 1).ToArray();
var v1 = new Int32[n + 1];
v0.CopyTo(v1, 0);
for (var i = 0; i < m; ++i)
{
v1[0] = i + 1;
for (var j = 0; j < n; ++j)
{
var substCost = (s1[i] == s2[j]) ? v0[j] : (v0[j] + 1);
var delCost = v0[j + 1] + 1;
var insCost = v1[j] + 1;
v1[j + 1] = Math.Min(substCost, delCost);
if (insCost < v1[j + 1])
{
v1[j + 1] = insCost;
}
}
var temp = v0;
v0 = v1;
v1 = temp;
}
return v0[n];
}
public static int Main()
{
string s1 = new String('a', 15000);
string s2 = s1;
string s3 = new String('b', 15000);
Stopwatch execTimer = new Stopwatch();
execTimer.Start();
Console.WriteLine(LevDist(s1, s2));
Console.WriteLine(LevDist(s1, s3));
execTimer.Stop();
double execTime = execTimer.ElapsedMilliseconds / 1000.0;
Console.WriteLine($"Finished in {execTime:0.000}s");
return 0;
}
}module main;
import core.time;
import std.stdio;
import std.algorithm : swap;
import std.array : array;
import std.range : iota, replicate;
long levDist(ref const string s1,
ref const string s2) pure nothrow @trusted
{
const auto m = s1.length;
const auto n = s2.length;
if (m == 0)
{
return n;
}
else if (n == 0)
{
return m;
}
long[] v0 = iota(0, long(n) + 1).array;
long[] v1 = v0.dup;
size_t i = 0;
foreach (ref c1; s1)
{
v1[0] = i + 1;
size_t j = 0;
foreach (ref c2; s2)
{
const auto substCost = (c1 == c2) ? v0[j] : (v0[j] + 1);
const auto delCost = v0[j + 1] + 1;
const auto insCost = v1[j] + 1;
// min(substCost, delCost, insCost) is slow.
v1[j + 1] = (substCost < delCost) ? substCost : delCost;
if (insCost < v1[j + 1])
{
v1[j + 1] = insCost;
}
++j;
}
swap(v0, v1);
++i;
}
return v0[n];
}
void main(string[] args)
{
string s1 = "a".replicate(15000);
string s2 = s1;
string s3 = "b".replicate(15000);
auto startTime = MonoTime.currTime;
writeln(levDist(s1, s2));
writeln(levDist(s1, s3));
auto endTime = MonoTime.currTime;
auto execTime = (endTime - startTime).total!"msecs" / 1000.0;
stderr.writefln("Finished in %.3fs", execTime);
}package main
import (
"bytes"
"fmt"
"os"
"time"
)
func levDist(s1, s2 []byte) int {
m := len(s1)
n := len(s2)
// Edge cases.
if m == 0 {
return n
} else if n == 0 {
return m
}
root := make([]int, (n+1)*2)
v0 := root[:n+1]
v1 := root[n+1:]
for i, _ := range v0 {
v0[i] = i
}
copy(v1, v0)
for i, c1 := range s1 {
v1[0] = i + 1
for j, c2 := range s2 {
substCost := v0[j]
if c1 != c2 {
substCost++
}
delCost := v0[j+1] + 1
insCost := v1[j] + 1
if substCost < delCost {
v1[j+1] = substCost
} else {
v1[j+1] = delCost
}
if insCost < v1[j+1] {
v1[j+1] = insCost
}
}
v0, v1 = v1, v0
}
return v0[n]
}
func main() {
s1 := bytes.Repeat([]byte("a"), 15000)
s2 := s1
s3 := bytes.Repeat([]byte("b"), 15000)
startTime := time.Now()
fmt.Println(levDist(s1, s2))
fmt.Println(levDist(s1, s3))
execTime := time.Now().Sub(startTime).Seconds()
fmt.Fprintf(os.Stderr, "Finished in %.3fs\n", execTime)
}use std::cmp::min;
use std::time::Instant;
fn lev_dist(s1: &str, s2: &str) -> i32 {
let m = s1.len();
let n = s2.len();
// Edge cases.
if m == 0 {
return n as i32;
} else if n == 0 {
return m as i32;
}
let mut v0: Vec = (0..).take(n + 1).collect();
let mut v1 = v0.to_vec();
for (i, c1) in s1.bytes().enumerate() {
unsafe {
*v1.get_unchecked_mut(0) = i as i32 + 1;
for (j, c2) in s2.bytes().enumerate() {
let mut subst_cost = *v0.get_unchecked(j);
if c1 != c2 {
subst_cost += 1;
}
let del_cost = *v0.get_unchecked(j + 1) + 1;
let ins_cost = *v1.get_unchecked(j) + 1;
let mut min_cost = min(subst_cost, del_cost);
if ins_cost < min_cost {
min_cost = ins_cost;
}
*v1.get_unchecked_mut(j + 1) = min_cost;
}
}
std::mem::swap(&mut v0, &mut v1);
}
return v0[n];
}
fn main() {
let s1 = "a".repeat(15000);
let s2 = &s1;
let s3 = "b".repeat(15000);
let start_time = Instant::now();
println!("{}", lev_dist(&s1, &s2));
println!("{}", lev_dist(&s1, &s3));
let exec_time = start_time.elapsed().as_millis() as f64 / 1000.0;
eprintln!("Finished in {:.3}s", exec_time);
} const std = @import("std");
const time = std.time;
const Allocator = std.mem.Allocator;
pub fn lev_dist(allocator: *Allocator, s1: []const u8, s2: []const u8) !i32 {
@setRuntimeSafety(false);
const m = s1.len;
const n = s2.len;
// Edge cases.
if (m == 0) {
return @intCast(i32, n);
} else if (n == 0) {
return @intCast(i32, m);
}
var root = try allocator.alloc(i32, (n + 1) * 2);
defer allocator.free(root);
var v0 = root[0..(n + 1)];
var v1 = root[(n + 1)..];
for (v0) |*it, i| {
it.* = @intCast(i32, i);
}
std.mem.copy(i32, v1, v0);
for (s1) |c1, i| {
v1[0] = @intCast(i32, i) + 1;
for (s2) |c2, j| {
const subst_cost = if (c1 == c2) v0[j] else (v0[j] + 1);
const del_cost = v0[j + 1] + 1;
const ins_cost = v1[j] + 1;
// std.mem.min(i32, [_]i32{subst_cost, del_cost, ins_cost}) is slow.
v1[j + 1] = if (subst_cost < del_cost) subst_cost else del_cost;
if (ins_cost < v1[j + 1]) {
v1[j + 1] = ins_cost;
}
}
std.mem.swap([]i32, &v0, &v1);
}
return v0[n];
}
pub fn main() !void {
const allocator = std.heap.page_allocator;
const stdout = &(try std.io.getStdOut()).outStream().stream;
const s1 = [_]u8{'a'} ** 15000;
const s2 = s1;
const s3 = [_]u8{'b'} ** 15000;
var exec_timer = try time.Timer.start();
try stdout.print("{}\n", try lev_dist(allocator, s1, s2));
try stdout.print("{}\n", try lev_dist(allocator, s1, s3));
const exec_time = @intToFloat(f64, exec_timer.read()) / time.ns_per_s;
std.debug.warn("Finished in {d:.3}s\n", exec_time);
}program main(output);
uses
sysutils, dateutils;
function levDist(const s1: AnsiString; const s2: AnsiString): longint;
var
m, n: NativeUint;
i, j: NativeUint;
c1, c2: AnsiChar;
v0, v1, temp: array of longint;
substCost, delCost, insCost: longint;
begin
m := length(s1);
n := length(s2);
// Edge cases.
if m = 0 then
exit(n)
else if n = 0 then
exit(m);
setLength(v0, n+1);
for i := 0 to n do
v0[i] := i;
v1 := copy(v0, 0, n+1);
i := 0;
for c1 in s1 do
begin
j := 0;
v1[0] := i + 1;
for c2 in s2 do
begin
substCost := v0[j];
if c1 <> c2 then
inc(substCost);
delCost := v0[j+1] + 1;
insCost := v1[j] + 1;
if substCost < delCost then
v1[j+1] := substCost
else
v1[j+1] := delCost;
if insCost < v1[j+1] then
v1[j+1] := insCost;
inc(j);
end;
temp := v0;
v0 := v1;
v1 := temp;
inc(i);
end;
exit(v0[n]);
end;
var
i: integer;
s1, s2, s3: AnsiString;
startTime, execTime: TDateTime;
begin
s1 := '';
s3 := '';
for i := 1 to 15000 do
begin
s1 := s1 + 'a';
s3 := s3 + 'b';
end;
s2 := s1;
startTime := now;
writeln(levDist(s1, s2));
writeln(levDist(s1, s3));
execTime := secondSpan(startTime, now);
writeln(stderr, format('Finished in %.3fs', [execTime]));
end.
import strformat, strutils, times
{.push checks: off.}
func levDist(s1, s2: string): int32 =
let m = s1.len
let n = s2.len
# Edge cases.
if m == 0: return int32(n)
elif n == 0: return int32(m)
var v0 = newSeq[int32](n + 1)
for i, _ in v0:
v0[i] = int32(i)
var v1 = v0
for i, c1 in s1:
v1[0] = int32(i) + 1
for j, c2 in s2:
let delCost = v0[j + 1] + 1
let insCost = v1[j] + 1
var substCost = v0[j]
if c1 != c2:
inc(substCost)
# min([substCost, delCost, insCost]) is slow.
v1[j + 1] = min(substCost, delCost)
if insCost < v1[j + 1]:
v1[j + 1] = insCost
swap(v0, v1)
result = v0[n]
{.pop.}
let s1 = repeat("a", 15000)
let s2 = s1
let s3 = repeat("b", 15000)
let startTime = cpuTime()
echo levDist(s1, s2)
echo levDist(s1, s3)
let execTime = cpuTime() - startTime;
stderr.write &"Finished in {execTime:.3f}s\n";import java.util.Arrays;
import java.util.stream.LongStream;
import java.lang.Math;
public class LevDist
{
public static long levDist(String s1, String s2)
{
return levDist(s1.getBytes(), s2.getBytes());
}
public static long levDist(byte[] s1, byte[] s2)
{
int m = s1.length;
int n = s2.length;
// Edge cases.
if (m == 0) {
return n;
} else if (n == 0) {
return m;
}
long[] v0 = LongStream.range(0, n + 1).toArray();
long[] v1 = v0.clone();
int i = 0, j;
for (byte c1 : s1) {
v1[0] = i + 1;
j = 0;
for (byte c2 : s2) {
long substCost = (c1 == c2) ? v0[j] : (v0[j] + 1);
long delCost = v0[j + 1] + 1;
long insCost = v1[j] + 1;
v1[j + 1] = Math.min(substCost, delCost);
if (insCost < v1[j + 1]) {
v1[j + 1] = insCost;
}
++j;
}
long[] temp = v0;
v0 = v1;
v1 = temp;
++i;
}
return v0[n];
}
public static void main(String[] args)
{
byte[] s1 = new byte[15000];
byte[] s2 = s1;
byte[] s3 = new byte[15000];
Arrays.fill(s1, (byte) 'a');
Arrays.fill(s3, (byte) 'b');
long execTime = -System.nanoTime();
System.out.println(levDist(s1, s2));
System.out.println(levDist(s1, s3));
execTime += System.nanoTime();
System.err.printf("Finished in %.3fs%n", execTime / 1000000000.0);
}
}Интерпретируемые языки
Снова наблюдения:
- Привычно думать, что V8 — более эффективный JS-движок. Не в этой задаче.
- Кое-где мы не дождались результатов вычислений (там, где значок ∞).
- Python для вычислений так себе. Pypy уже можно, но лучше всё-таки Julia.
- Octave хорошо работает с матрицами, а тут задача имеет совершенно нематричную форму, так что увы.
- Про Raku хочется пошутить, но не буду. Мне же не 12 лет, в конце концов.
#!/usr/bin/env julia
using Base: @pure, stderr
using Printf
@pure function lev_dist(s1::AbstractString, s2::AbstractString)::Int32
m, n = sizeof(s1), sizeof(s2)
m == 0 && return n
n == 0 && return m
ca1, ca2 = codeunits(s1), codeunits(s2)
v0::Vector{Int32} = collect(0:n)
v1 = copy(v0)
@inbounds begin
for (i, c1) in enumerate(ca1)
v1[1] = i
for (j, c2) in enumerate(ca2)
subst_cost = v0[j] + ((c1 === c2) ? 0 : 1)
del_cost = v0[j + 1] + 1
ins_cost = v1[j] + 1
v1[j + 1] = min(subst_cost, del_cost, ins_cost)
end
v0, v1 = v1, v0
end
end
return v0[n + 1]
end
let
s1 = 'a'^15000
s2 = s1
s3 = 'b'^15000
exec_time = @elapsed begin
println(lev_dist(s1, s2))
println(lev_dist(s1, s3))
end
@printf(stderr, "Finished in %.3fs\n", exec_time)
end
function stringToByteArray(s) {
let a = [];
for (let c of s) {
c = c.charCodeAt(0);
do {
a.unshift(c & 0xFF);
c >>= 8;
} while (c !== 0);
}
return a;
}
function levDist(s1, s2) {
if (typeof s1 === "string" || s1 instanceof String) {
s1 = stringToByteArray(s1);
}
if (typeof s2 === "string" || s2 instanceof String) {
s2 = stringToByteArray(s2);
}
const m = s1.length;
const n = s2.length;
// Edge cases.
if (m == 0) {
return n;
} else if (n == 0) {
return m;
}
let v0 = [];
for (let i = 0; i <= n; ++i) {
v0[i] = i;
}
let v1 = v0.slice();
for (let i = 0; i < m; ++i) {
v1[0] = i + 1;
for (let j = 0; j < n; ++j) {
const substCost = v0[j] + ((s1[i] === s2[j]) ? 0 : 1);
const delCost = v0[j + 1] + 1;
const insCost = v1[j] + 1;
// Math.min(substCost, delCost, insCost) is slow.
v1[j + 1] = (substCost < delCost) ? substCost : delCost;
if (insCost < v1[j + 1]) {
v1[j + 1] = insCost;
}
}
[v0, v1] = [v1, v0];
}
return v0[n];
}
var s1 = new Uint8Array(15000);
var s2 = s1;
var s3 = new Uint8Ar
