Быстрая медианная фильтрация с использованием AVX-51231.10.2020 23:02

Недавно Боб Стигалл сделал в конференции CppCon 2020 доклад под названием «Adventures in SIMD-thinking», где он среди прочего рассказывал о своем опыте использования AVX512 для медианной фильтрации с окном 7. Этот доклад вызвал у меня двоякие чувства: с одной стороны, прикольно сделано, и заявлено почти 20-кратное ускорение по сравнению с «тупейшей» реализацией через STL; с другой стороны, за один проход алгоритма из 16 входных семплов у него получалось всего 2 выходных, хотя входных данных хватало на 10, да и некоторые детали реализации вызвали желание попытаться их улучшить. Я подумал-подумал, и придумал идею, потом еще, потом попробовал их «в софте» и понял, что у меня появилось что-то, чем можно поделиться :) Так и получилась эта статья.

Базовая реализация

Кратко опишу, как оно было сделано у Боба (по сути, краткий пересказ соответствующей части его рассказа вместе с его же картинками). Он сделал с использованием AVX512 следующие примитивы (я опущу те из описанных им примитивов, которые напрямую соответствуют единственной операции AVX512):

rotate: сдвиг элементов в регистре AVX-512 по кругу

shift with carry: сдвиг элементов из регистра с замещением элементами из второго регистра

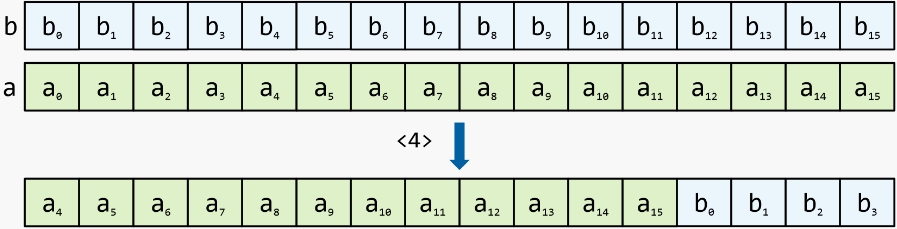
in place shift with carry: как shift with carry, но входные регистры передаются по ссылке и результат сдвига остается в них же

compare with exchange: параллельная сортировка до 8 пар элементов в регистре

Это основной примитив для фильтрации, и самый сложный, поэтому про него стоит сказать чуть подробнее: в perm помещаются индексы 0…15, причем индексы каждой сортируемой пары переставлены местами; в mask помещаются биты 1 в «старшей» позиции каждой сортируемой пары. Идея проста: вычисляются поэлементный минимум и максимум между входными данными и данными, перестановленными в соответствии с perm. В результате для каждой сортируемой пары в vmin получаем меньшее значение из пары в обеих позициях пары, а в vmax соответственно бо́льшее значение из пары. Далее просто объединяем оба результата так, чтобы минимум и максимум оказались на нужных нам позициях.

Все, примитивы кончились, можно делать алгоритм. На каждой итерации цикла:

1) используя shift with carry, загоняем в «рабочий» регистр входные данные так, чтобы край окна фильтрации был в самом «левом» элементе регистра (т.е. окно для выходного элемента 0 будет состоять из входных элементов 0…6, для элемента 1 — из элементов 1…7 и т. д.)

2) переставляем элементы так, чтобы окно для элемента 0 было в одной половине регистра, а окно для элемента 1 — во второй

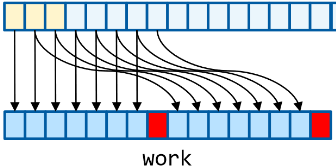
3) Делаем сортировочную сеть для 7 элементов, параллельно сразу для обоих массивов — это 6 итераций compare and exchange, после которых получаем два сортированных массива в регистре. Остается достать срединные элементы из обоих массивов — это и будут наши отсортированные данные — и положить их в выходной регистр и потом в память.

Если из этого объяснения ничего не понятно, то перед продолжением чтения стоит обратиться к первоисточнику, где Боб Стигалл все объясняет много подробнее (и, наверное, много понятнее)

Шаг оптимизации 0

Прежде чем что-то оптимизировать, надо научиться оценивать правильность и результативность оптимизации. Поэтому сначала надо найти исходные коды того, что сделал Боб, и положить их в бенчмарк (я выбрал размер данных, чтобы они убирались в кеш L2). Заодно добавлю проверку того, что разные подходы к фильтрации возвращают одинаковые результаты на одинаковых данных. И надо найти машину с поддержкой AVX-512…

Шаг оптимизации 1

Первое, что бросается в глаза в алгоритме — это сортировка массивов. Независимо сортируются два массива по 7 элементов;, но у них 6 общих элементов и от результата сортировки нужен единственный центральный элемент!

Может быть, будет быстрее один раз отсортировать один массив из 6 общих элементов r1-r6 и сделать две сортировки вставками, для r0 и r7? Пусть у нас есть отсортированный массив S[0…5], и элемент X, который надо в него вставить, но нам интересно только значение S[3] после вставки.

Если X >= S[3], то S[3] остается на своем месте, и нам нужно его значение
Если X <= S[2], то S[2] сдвигается на место S[3], и нам нужно значение S[2]
Если S[2] < X < S[3], то X встает на место S[3], сдвигая его выше, и нам нужно значение X. Получается, что нам нужно clamp(X, S[2], S[3]) => min(max(X, S[2]), S[3])!

Получаем новый алгоритм:

собрать «края» у 4 7-элементных массивов (элементы 0, 7, 2, 9) — это элементы X для 4 результатов
развести 6-элементные массивы 1…6 и 3…8 по отдельным линиям (пусть будут 0…7 и 8…15, как и было)
отсортировать оба 6-элементных массива
сделать clamp элементами 2 и 3 первого массива на элементы X[0] и X[1], и элементами 2 и 3 второго массива на элементы X[2] и X[3]

По прикидкам должно получиться примерно 2x ускорение — число операций сортировки в расчете на один выходной элемент уменьшается более чем в 2 раза (поскольку сортировочная сеть для 6 элементов требует 5 итераций, а для 7 элементов — 6), но clamp приблизительно соответствует одной итерации сортировочной сети. Проверяем в бенчмарке: 1,86x раз. Неплохо. Что еще можно ускорить?

Шаг 2

На «концевые» элементы X больше не смотрим. Обратим внимание на 6-элементные массивы; данных хватает на 5 таких массивов, но используется только 2 (поскольку для сортировки 3 уже не хватает места в регистре). Обратим внимание на первую итерацию сортировки каждого из массивов — это попарная сортировка: S[0] <=> S[1], S[2] <=> S[3], S[4] <=> S[5]

Массивы же смещены друг относительно друга на 2, т. е. если мы сделаем попарную сортировку во всем регистре еще до того, как разнесем массивы по половинам регистра, то выполним первый шаг сортировки во всех массивах сразу!

Получается простая оптимизация — разворачиваем внутренний цикл в 2 раза и делаем первую итерацию один раз, а уже потом можно по очереди брать и сортировать по 2 массива. Делаем, проверяем: 1.06x. Мелочь, а приятно.

Шаг 3

Можно было бы что-то выжать из последней итерации сортировки, но мы пойдем другим путем и попробуем повторить шаг 1, но уже с 6-элементными массивами.

Как видим, массивы пересекаются 4 элементами (зеленые области на картинке), а нам интересны только два элемента из 6; может быть, можно отсортировать эти 4-элементные массивы и потом вставить два оставшихся элемента?

От оптимизации с шага 2 можно не отказываться, поскольку у 4-элементной сортировочной сети первый шаг точно такой же. Тогда у нас получается для каждого 6-элементного массива: 2-элементный отсортированный массив Y и 4-элементный сортированный массив S, и нам интересны элементы 2 и 3 после слияния этих двух массивов (назовем конечный массив Z). Заметим, что min(Y[0], S[0]) => Z[0], который нам неинтересен; max(Y[0], S[0]) окажется одним из Z[1]…Z[5] — он интересен. Аналогично max(Y[1], S[3]) не интересен, а интересен только min(Y[1], S[3]).

У нас получается 4-элементный массив из S[1], S[2], и двух результатов min/max. Его нужно снова отсортировать, но зато мы можем сортировать все 4 таких массива вместе, и потом взять из каждого элементы 1 и 2 — это будут элементы 2 и 3 из оригинальных 6-элементного массива. Также заметим, что последний шаг у «первой» 4-элементной сортировочной сети сортирует между собой элементы S[1] и S[2], а нам их порядок не важен — все равно нужно пересортировать. Поэтому его можно смело выбросить, и от первой сети остается всего 2 итерации, одна из которых заодно сортирует наши массивы Y.

Поэтому вырисовывается такой алгоритм:

сортируем попарно r1-r2 и т. д.
сохраняем результат в отдельный регистр — это наши массивы Y, соответственно r1–2, r5–6, r7–8, r11–12; через permute сразу сформируем заготовку под 4 массива для второй сортировки, перенеся Y в r0–1, r4–5 и т. д.
делаем вторую (и последнюю) итерацию «первой» сортировочной сети; получаем в r3-r6 и r7-r10 частично сортированные массивы
вычисляем max и min соответственно для каждой пары Y[0]/S[0], Y[1]/S[3] и сохраняем результат обратно в регистр с заготовкой под массивы
делаем mask_permute для регистров Y и S, перенося S[1] и S[2] на их законные места и получая массивы, которые предстоит отсортировать
сортируем 4 массива параллельно
далее берем из каждого элементы 1 и 2, и через min/max с элементами X получаем 8 выходных результатов

Выглядит сложно, но должно быть быстрее, чем две развернутых итерации, получившиеся у нас в шаге 2. Пробуем — в 1.64x раза быстрее, чем шаг 2, и в 3 с лишним раза быстрее, чем оригинальная реализация.

Идеи по улучшению алгоритма на этом кончились; можно еще подобрать крошки в рамках имеющегося (точно можно избавиться от одного-двух permute; вероятно, еще что-то найдется), но этого я пока не делал.

Выводы

Издевательства над красивым алгоритмом иногда могут сделать его уродливым, но более быстрым :)

Повторю результаты benchmark:

на 512 кБ данных: ускорение примерно в 3.1–3.2 раза; в 7.3 раза медленнее, чем простой memcpy через регистр avx-512
на 50 МБ данных: ускорение в 2.8–2.9 раза; в 1.8 раза медленнее, чем memcpy (!)

Тормознутость основной памяти современных компьютеров не устает меня поражать.

Применимость для окон других размеров

Можно ли похожим образом ускорить медианный фильтр с окном 5? Думаю, что да (disclaimer: не проверялось даже на бумажке — исключительно умозрительные измышления).

В 16-элементном регистре хранится достаточно данных для вычисления 12 результатов.

Оригинальный алгоритм Боба — можно сделать вычисление 3 элементов (вообще неудобно для цикла…)
идея из шага 1 замечательно работает, и мы получаем одновременную обработку 4 (из 6 возможных) 4-элементных массивов — одновременно ускоряя сортировку, т. к. сортировочная сеть для 4 элементов короче, чем для 5 элементов; получаем 8 результатов.
шаг 2 сделать можно, но не имеет смысла — на вторую итерацию из имеющихся данных остается всего 2 массива; вероятно, будет выгоднее вместо их обработки сразу брать больше данных и делать следующую итерацию с начала.
шаг 3 сделать можно, и скорее всего будет иметь смысл. Первая сортировка вырождается в ничто, вторая — в единственную итерацию попарной сортировки, и в результате получаем все 12 результатов за один шаг цикла. Остается придумать, что делать с таким «некруглым» количеством — то ли вдвое раскрутить цикл и сохранять сразу по 24 значения, то ли писать в память по 12 результатов за шаг.

А что будет с окном 9? В регистре хранится достаточно данных для вычисления 8 результатов.

оригинальный алгоритм — всего один результат за шаг цикла
шаг 1 — в регистр убираются 2 8-элементных массива из 4 возможных, они нам дают 4 результата за шаг цикла (также уменьшаем длину сортировочной сети с 7 до 6 итераций)
шаг 2 — применим, но даст какие-то копейки
шаг 3 — сделать в принципе можно, но бессмысленно — 6-элементных массивов в регистр убирается всего 2, а дважды сортировать 6-элементный массив (даже если удастся сэкономить на том, что не нужны полностью сортированные массивы) наверняка обойдется дороже, чем один раз отсортировать 8-элементный.

Послесловие

Надеюсь, кому-нибудь эта статья оказалось интересной или полезной. Если хочется покопаться в этом самостоятельно, я выложил код всех шагов на https://github.com/tea/avx-median/. Писалось «на коленке», поэтому комментариев нет, названия взяты с потолка и вообще ужас-ужас. Описания алгоритмов из статьи придут на помощь желающим разобраться в том, что же там такое сделано.

Если у вас после прочтения возникли какие-либо идеи по поводу того, как еще можно оптимизировать медианную фильтрацию — буду рад их услышать. Благодарю за внимание.