Библиотеки для глубокого обучения Theano/Lasagne
Привет, Хабр!

Параллельно с публикациями статей открытого курса по машинному обучению мы решили запустить ещё одну серию — о работе с популярными фреймворками для нейронных сетей и глубокого обучения.
Я открою этот цикл статьёй о Theano — библиотеке, которая используется для разработки систем машинного обучения как сама по себе, так и в качестве вычислительного бекэнда для более высокоуровневых библиотек, например, Lasagne, Keras или Blocks.
Theano разрабатывается с 2007 года главным образом группой MILA из Университета Монреаля и названа в честь древнегреческой женщины-философа и математика Феано (предположительно изображена на картинке). Основными принципами являются: интеграция с numpy, прозрачное использование различных вычислительных устройств (главным образом GPU), динамическая генерация оптимизированного С-кода.
Будем придерживаться следующего плана:
- Предисловие или лирическое отступление о библиотеках для глубокого обучения
- Введение
- Установка
- Настройка
- Основы
- Первые шаги
- Переменные и функции
- Разделяемые переменные и еще о функциях
- Отладка
- Машинное обучение на Theano
- Логистическая регрессия
- SVM
- Нелинейные признаки
- Lasagne
- Многослойный перцептрон
- Заключение
Код с примерами из этого поста можно найти тут.
Предисловие или лирическое отступление о библиотеках для глубокого обучения
В настоящее время разработаны десятки библиотек для работы с нейронными сетями, все они, подчас существенно, различаются в реализации, но можно выявить два основных подхода: императивный и символьный. 1
Давайте посмотрим на примере, чем они различаются. Предположим, что мы хотим вычислить простое выражение
Вот так оно выглядело бы в императивном изложении на языке python:
a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1Интерпретатор исполняет код построчно, сохраняя результаты в переменных a, b, c и d.
Та же программа в символьной парадигме выглядела бы так:
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# компиляция функции
f = compile(D)
# исполнение
d = f(A=np.ones(10), B=np.ones(10)*2) Существенное различие заключается в том, что когда мы объявляем
Существенное различие заключается в том, что когда мы объявляем D, исполнения не происходит, мы лишь задали граф вычислений, который затем скомпилировали и наконец выполнили.
Оба подхода имеют свои достоинства и недостатки. В первую очередь, императивные программы гибче, нагляднее и проще в отладке. Мы можем использовать все богатства используемого языка программирования, например, циклы и ветвления, выводить промежуточные результаты в отладочных целях. Такая гибкость достигается, в первую очередь, малыми ограничениями, накладываемыми на интерпретатор, который должен быть готов к любому последующему использованию переменных.
С другой стороны, символьная парадигма накладывает больше ограничений, но вычисления получаются более эффективными, как по памяти, так и по скорости исполнения: на этапе компиляции можно применить ряд оптимизаций, выявить неиспользуемые переменные, выполнить часть вычислений, переиспользуя память и так далее. Отличительная черта символьных программ — отдельные этапы объявления графа, компиляции и выполнения.
Мы останавливаемся на этом так подробно, потому что императивная парадигма знакома большинству программистов, в то время как символьная может показаться непривычной, и Theano, как раз, явный пример символьного фреймворка.
Тем, кому хочется разобраться в этом вопросе подробнее, рекомендую почитать соответствующий раздел документации к MXNet (об этой библиотеке мы еще напишем отдельный пост), но ключевой момент для понимания дальнейшего текста заключается в том, что программируя на Theano, мы пишем на python программу, которую потом скомпилируем и выполним.
Но довольно теории, давайте разбираться с Theano на примерах.
Установка
Для установки нам понадобятся: python версии старше 2.6 или 3.3 (лучше dev-версию), компилятор С++ (g++ для Linux или Windows, clang для MacOS), библиотека примитивов линейной алгебры (например ATLAS, OpenBLAS, Intel MKL), NumPy и SciPy.
Для выполнения вычислений на GPU понадобится CUDA, а ряд операций, встречающихся в нейронных сетях, можно ускорить с помощью сuDNN. Начиная с версии 0.8.0, разработчики Theano рекомендуют использовать libgpuarray, что также даёт возможность использовать несколько GPU.
Когда все зависимости установлены, можно установить Theano через pip:
# последний релиз
pip install Theano
# последняя версия из репозитория
pip install --upgrade https://github.com/Theano/Theano/archive/master.zipНастройка
Theano можно настроить тремя способами:
- Выставив атрибуты объекта
theano.configв нужное значение - Через переменную окружения
THEANO_FLAGS - Через конфигурационный файл
$HOME/.theanorc(или$HOME/.theanorc.txtпод Windows)
Я обычно использую примерно такой конфигурационный файл:
[global]
device = gpu # выбирает устройство, на котором будет выполняться наш код - GPU или CPU
floatX = float32
optimizer_including=cudnn
allow_gc = False # быстрее, но использует больше памяти
#exception_verbosity=high
#optimizer = None # полезно при отладке
#profile = True
#profile_memory = True
config.dnn.conv.algo_fwd = time_once # эти две опции зачастую приводят к ускорению свёрток
config.dnn.conv.algo_bwd = time_once
[lib]
Cnmem = 0.95 # позволяет включить CNMeM (https://github.com/NVIDIA/cnmem) - менеджер CUDA-памятиПодробнее о конфигурации можно узнать в документации.
Основы
Первые шаги
Теперь, когда всё установлено и настроено, давайте попробуем написать немного кода, например, вычислим значение многочлена в точке 10:
import theano
import theano.tensor as T
# объявим theano-переменную
a = T.lscalar()
# определим выражение
expression = 1 + 2 * a + a ** 2
# скомпилируем theano-функцию
f = theano.function(
inputs=[a], # аргументы
outputs=expression # результат
)
# запустим вычисление
f(10)
>>> array(121)Здесь мы совершили 4 вещи: определили скалярную переменную а типа long, создали выражение, содержащее наш многочлен, определили и скомпилировали функцию f, а также выполнили её, передав на вход число 10.
Обратим внимание на тот факт, что переменные в Theano — типизированные, причем тип переменной содержит информацию как о типе данных, так и о их размерности, т.е. чтобы посчитать наш многочлен сразу в нескольких точках, потребуется определить а как вектор:
a = T.lvector()
expression = 1 + 2 * a + a ** 2
f = theano.function(
inputs=[a],
outputs=expression
)
arg = arange(-10, 10)
res = f(arg)
plot(arg, res, c='m', linewidth=3.)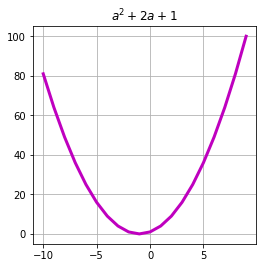
В данном случае нам нужно только указать количество измерений переменной при инициализации: размер каждого измерения вычисляется автоматически на этапе вызова функции.
Пакет theano.tensor содержит наиболее часто употребляемые типы тензоров, однако, нетрудно определить и свой тип.
При несовпадении типов Theano выбросит исключение. Исправить это, кстати как и поменять многое другое в работе функций, можно, передав конструктору аргумент allow_input_downcast=True:
x = T.dmatrix('x')
v = T.fvector('v')
z = v + x
f = theano.function(
inputs=[x, v],
outputs=z,
allow_input_downcast=True
)
f_fail = theano.function(
inputs=[x, v],
outputs=z
)
print(f(ones((3, 4), dtype=float64), ones((4,), dtype=float64))
>>> [[ 2. 2. 2. 2.]
>>> [ 2. 2. 2. 2.]
>>> [ 2. 2. 2. 2.]]
print(f_fail(ones((3, 4), dtype=float64), ones((4,), dtype=float64))
>>> ---------------------------------------------------------------------------
>>> TypeError Traceback (most recent call last)Мы также можем вычислять несколько выражений сразу, оптимизатор в этом случае может переиспользовать пересекающиеся части, в данном случае сумму :
x = T.lscalar('x')
y = T.lscalar('y')
square = T.square(x + y)
sqrt = T.sqrt(x + y)
f = theano.function(
inputs=[x, y],
outputs=[square, sqrt]
)
print(f(5, 4))
>>> [array(81), array(3.0)]
print(f(2, 2))
>>> [array(16), array(2.0)]Для обмена состояниями между функциями используются специальные shared переменные:
state = theano.shared(0)
i = T.iscalar('i')
inc = theano.function([i],
state,
# обновим разделяемую переменную
updates=[(state, state+i)])
dec = theano.function([i],
state,
updates=[(state, state-i)])
# разделяемые переменные могут менять значения сразу нескольких функций
print(state.get_value())
inc(1)
inc(1)
inc(1)
print(state.get_value())
dec(2)
print(state.get_value())
>>> 0
>>> 3
>>> 1Значения таких переменных, в отличие от тензорных, можно получать и модифицировать вне Theano-функций из обычного python-кода:
state.set_value(-15)
print(state.get_value())
>>> -15Значения в shared переменных можно «подставлять» в тензорные переменные:
x = T.lscalar('x')
y = T.lscalar('y')
i = T.lscalar('i')
expression = (x - y) ** 2
state = theano.shared(0)
f = theano.function(
inputs=[x, i],
outputs=expression,
updates=[(state, state+i)],
# подставим значение переменной state в граф вместо y
givens={
y : state
}
)
print(f(5, 1))
>>> 25
print(f(2, 1))
>>> 1Отладка
Theano предоставляет ряд средств для отображения графа вычислений и отладки. Тем не менее, отладка символьных выражений по-прежнему остаётся задачей не из лёгких. Мы кратко перечислим тут наиболее употребимые подходы, подробнее об отладке можно прочитать в документации: http://deeplearning.net/software/theano/tutorial/printing_drawing.html
Мы можем распечатать граф вычислений для каждой функции:
x = T.lscalar('x')
y = T.lscalar('y')
square = T.square(x + y)
sqrt = T.sqrt(x + y)
f = theano.function(
inputs=[x, y],
outputs=[square, sqrt]
)
# сумма будет подсчитана только один раз
theano.printing.debugprint(f)Заметьте, что сумма вычисляется только один раз:
Elemwise{Sqr}[(0, 0)] [id A] '' 2
|Elemwise{add,no_inplace} [id B] '' 0
|x [id C]
|y [id D]
Elemwise{sqrt,no_inplace} [id E] '' 1
|Elemwise{add,no_inplace} [id B] '' 0Выражения можно выводить и в более лаконичной форме:
# определим выражение
W = T.fmatrix('W')
b = T.fvector('b')
X = T.fmatrix('X')
expr = T.dot(X, W) + b
prob = 1 / (1 + T.exp(-expr))
pred = prob > 0.5
# и распечатаем его
theano.pprint(pred)
>>> 'gt((TensorConstant{1} / (TensorConstant{1} + exp((-((X \\dot W) + b))))), TensorConstant{0.5})'Или в виде графа:
theano.printing.pydotprint(pred, outfile='pics/pred_graph.png', var_with_name_simple=True)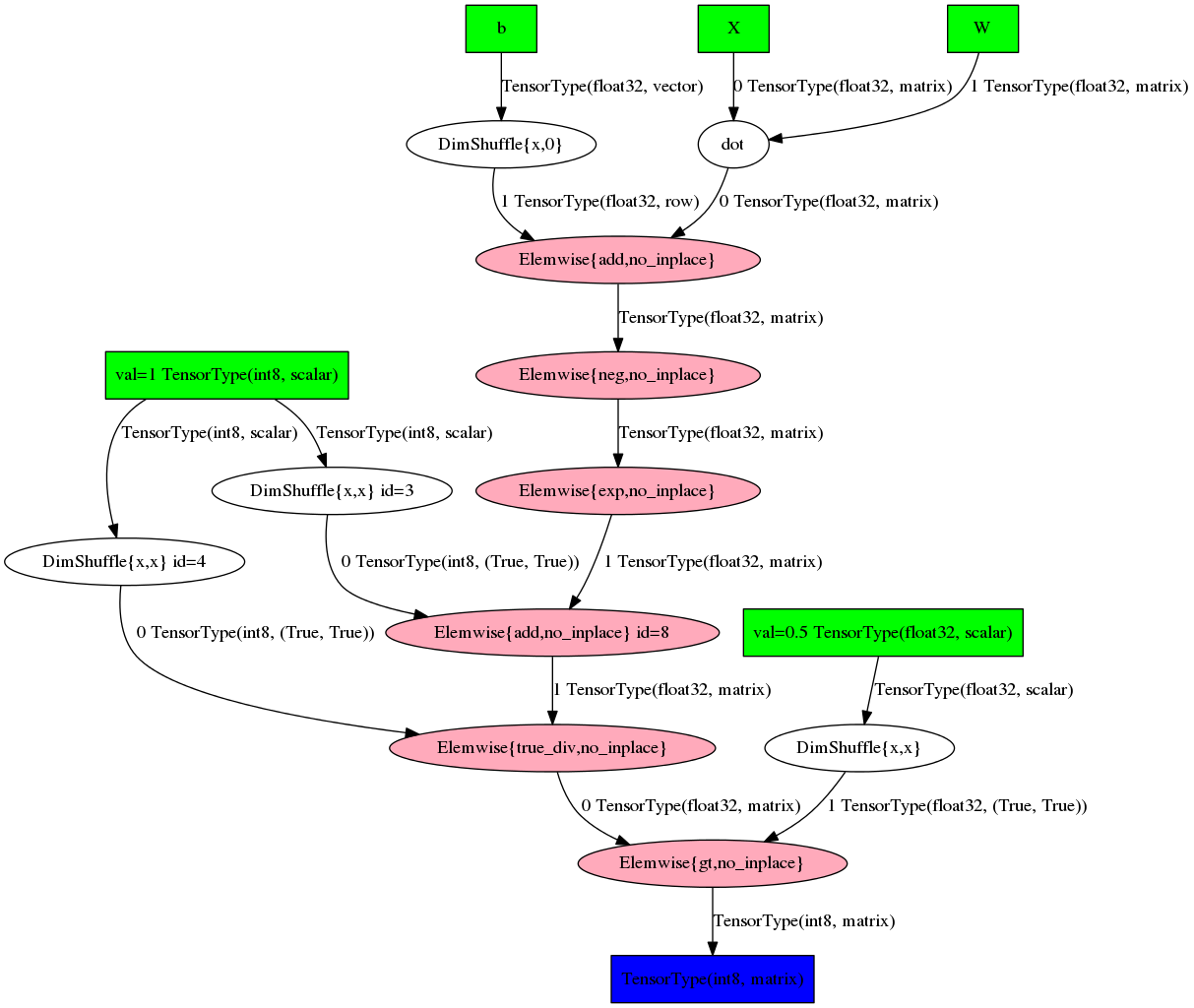
К сожалению, читаемость таких графов резко падает с ростом сложности выражения. Фактически что-то понять можно только на игрушечных примерах.
Машинное обучение на Theano
Логистическая регрессия
Давайте посмотрим на примере логистической регрессии, как с помощью Theano можно разрабатывать алгоритмы машинного обучения. Намеренно не будем вдаваться в подробности того, как устроена эта модель (оставим это до соответствующей статьи открытого курса), но напомним, что апостериорная вероятность класса имеет вид
Давайте определим параметры модели, для удобства введём отдельный параметр для смещения:
W = theano.shared(
value=numpy.zeros((2, 1),dtype=theano.config.floatX),
name='W')
b = theano.shared(
value=numpy.zeros((1,), dtype=theano.config.floatX),
name='b')И заведём символьные переменные для признаков и меток класса:
X = T.matrix('X')
Y = T.imatrix('Y')Давайте теперь определим выражения для апостериорной вероятности и предсказаний модели:
linear = T.dot(X, W) + b
p_y_given_x = T.nnet.sigmoid(linear)
y_pred = p_y_given_x > 0.5И определим функцию потерь вида:
loss = T.nnet.binary_crossentropy(p_y_given_x, Y).mean()Мы не стали выписывать выражения для сигмоиды и кросс-энтропии в явном виде, а воспользовались функциями из пакета theano.tensor.nnet, который предоставляет оптимизированные реализации ряда популярных в машинном обучении функций. Кроме того, функции из этого пакета обычно включают в себя дополнительные трюки для численной устойчивости.
Для оптимизации функции потерь давайте воспользуемся методом градиентного спуска, каждый шаг которого задаётся выражением:
Давайте воплотим его в коде:
g_W = T.grad(loss, W)
g_b = T.grad(loss, b)
updates = [(W, W - 0.04 * g_W),
(b, b - 0.08 * g_b)]Здесь мы воспользовались замечательной возможностью Theano — автоматическим2 дифференцированием. Вызов T.grad вернул нам выражение, которое будет содержать градиент первого аргумента по второму. Это может показаться излишним для столь простого случая, но очень выручает при построении больших, многослойных моделей.
Когда градиенты получены, нам остаётся лишь скомпилировать Theano-функции:
train = theano.function(
inputs=[X, Y],
outputs=loss,
updates=updates,
allow_input_downcast=True
)
predict_proba = theano.function(
[X],
p_y_given_x,
allow_input_downcast=True
)И запустить итеративный процесс:
sgd_weights = [W.get_value().flatten()]
for iter_ in range(4001):
loss = train(x, y[:, np.newaxis])
sgd_weights.append(W.get_value().flatten())
if iter_ % 100 == 0:
print("[Iteration {:04d}] Train loss: {:.4f}".format(iter_, float(loss)))Для сгенерированных мною данных процесс сходится к такой разделяющей прямой: 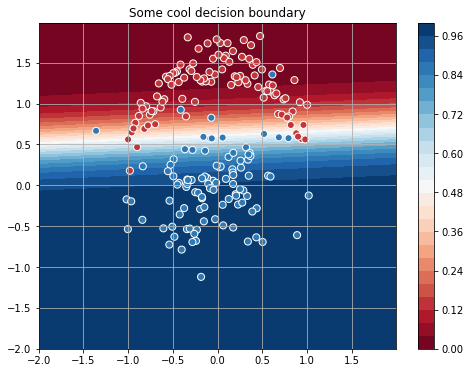
Выглядит неплохо, но кажется, что для такой простой задачи 4000 итераций — это как-то многовато… Давайте попробуем ускорить оптимизацию и воспользуемся методом Ньютона. Этот метод использует вторые производные функции потерь и представляет собой последовательность таких шагов:
где — матрица Гессе.
Чтобы посчитать матрицу Гессе, создадим одномерные версии параметров нашей модели:
W_init = numpy.zeros((2,),dtype=theano.config.floatX)
W_flat = theano.shared(W_init, name='W')
W = W_flat.reshape((2, 1))
b_init = numpy.zeros((1,), dtype=theano.config.floatX)
b_flat = theano.shared(b_init, name='b')
b = b_flat.reshape((1,))И определим шаг оптимизатора:
h_W = T.nlinalg.matrix_inverse(theano.gradient.hessian(loss, wrt=W_flat))
h_b = T.nlinalg.matrix_inverse(theano.gradient.hessian(loss, wrt=b_flat))
updates_newton = [(W_flat, W_flat - T.dot(h_W , g_W)),
(b_flat, b_flat - T.dot(h_b, g_b))]Хоть мы и пришли к тем же результатам,  ,
,
Методу Ньютона для этого понадобилось всего 30 (против 4000 у градиентного спуска) шагов.
Пути обоих методов можно посмотреть на этом графике: 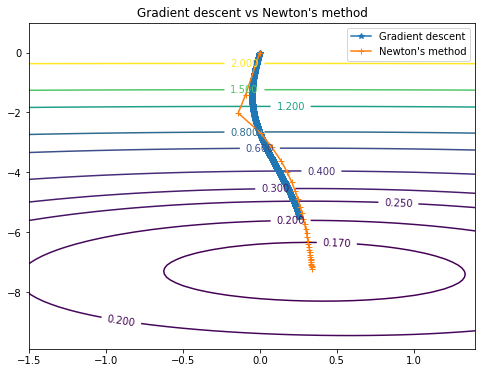
SVC
Так же мы без труда можем реализовать метод опорных векторов, для этого достаточно представить функцию потерь в следующем виде:
В терминах Theano это можно написать с помощью замены нескольких строк в предыдущем примере:
C = 10.
loss = C * T.maximum(0, 1 - linear * (Y * 2 - 1)).mean() + T.square(W).sum()
predict = theano.function(
[X],
linear > 0,
allow_input_downcast=True
)Для выбранного С классификатор разделит пространство так: 
Нелинейные признаки
Циклы являются одной из наиболее употребимых конструкций в программировании. Поддержка циклов в Theano представлена функцией scan. Давайте познакомимся с тем, как она работает. Думаю, читателям уже очевидно, что линейная функция от признаков — не лучший кандидат на разделение сгенерированных данных. Этот недостаток можно исправить, добавив полиномиальные признаки к исходным (этот приём подробно описан в другой статье нашего блога). Итак, хочется получить преобразование вида . В python мы могли бы реализовать его, например, так:
poly = []
for i in range(K):
poly.extend([x**i for x in features])В Theano это выглядит следующим образом:
def poly(x, degree=2):
result, updates = theano.scan(
# записываем выражение, вычисляющее каждую новую степень полинома
fn=lambda prior_result, x: prior_result * x,
# инициализируем выходной тензор
outputs_info=T.ones_like(x),
# укажем, что x надо передать в качестве второго аргумента fn
non_sequences=x,
# количество итераций
n_steps=degree)
# результат возвращаем в виде матрицы N x M*degree
return result.dimshuffle(1, 0, 2).reshape((result.shape[1],
result.shape[0] * result.shape[2]))Первой в scan передается функция, которая будет вызываться на каждой итерации, её первый аргумент — результат на предыдущей итерации, последующие — все non_sequences; outputs_info инициализирует выходной тензор такой же размерности и типа, как и x, и заполняет его единицами; n_steps указывает на требуемое количество итераций.scan вернет результат в виде тензора размера (n_steps, ) + outputs_info.shape, поэтому мы преобразуем его в матрицу, чтобы получить нужные признаки.
Проиллюстрируем работу полученного выражения простым примером:
[[1, 2], -> [[ 1, 2, 1, 4],
[3, 4], -> [ 3, 4, 9, 16],
[5, 6]] -> [ 5, 6, 25, 36]]Чтобы воспользоваться плодами своих усилий, достаточно поменять определение модели и добавить параметров (ведь признаков стало больше):
W = theano.shared(
value=numpy.zeros((8, 1),dtype=theano.config.floatX),
name='W')
linear = T.dot(poly(X, degree=4), W) + bНовые признаки позволяют значительно лучше разделить классы: 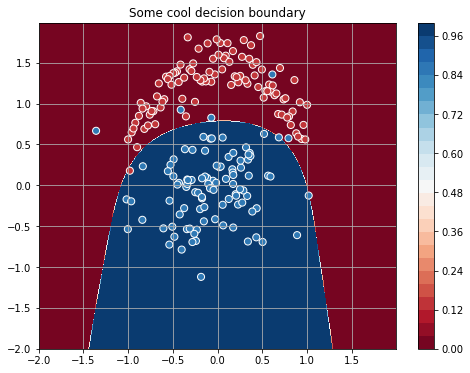
Нейронные сети и Lasagne3
К этому моменту мы уже обсудили основные этапы создания систем машинного обучения на Theano: инициализация входных переменных, определение модели, компиляция Theano-функций, цикл с шагами оптимизатора. На этом можно было бы и закончить, но очень уж хочется познакомить читателей с Lasagne — замечательной библиотекой для нейронных сетей, работающей поверх Theano. Lasagne предоставляет набор готовых компонентов: слоёв, алгоритмов оптимизации, функций потерь, инициализаций параметров и т.д., при этом не скрывает Theano за многочисленными слоями абстракций.
Рассмотрим, как может выглядеть типичный код на Theano/Lasagne на примере классификации MNIST’a.

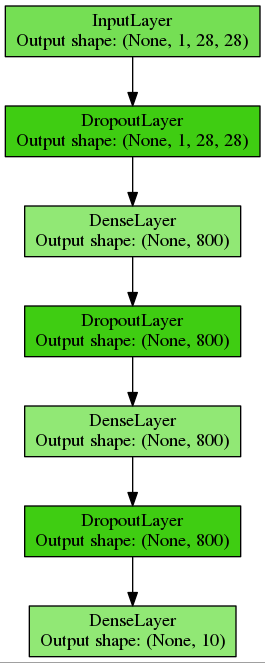
Сконструируем многослойный перцептрон с двумя скрытыми слоями по 800 нейронов, для регуляризации будем использовать dropout и разместим этот код в отдельной функции:
def build_mlp(input_var=None):
# Входной слой, определяющий размерность данных
# (переменный размер minibatch'a, 1 канал, 28 строк и 28 столбов)
# Мы можем передать тензорную переменную для входных данных,
# или же она будет создана для нас
network = lasagne.layers.InputLayer(
shape=(None, 1, 28, 28),
input_var=input_var)
# dropout на 20% для входных данных
network = lasagne.layers.DropoutLayer(network, p=0.2)
# Полносвязный слой на 800 нейронов и ReLU в качестве нелинейности
# также инициализируем веса методом, предложенным Xavier Glorot и Yoshua Bengio
network = lasagne.layers.DenseLayer(
network,
num_units=800,
nonlinearity=lasagne.nonlinearities.rectify,
W=lasagne.init.GlorotUniform())
# Добавим dropout еще на 50%:
network = lasagne.layers.DropoutLayer(network, p=0.5)
# И ещё один полносвязный слой
network = lasagne.layers.DenseLayer(
network,
num_units=800,
nonlinearity=lasagne.nonlinearities.rectify)
network = lasagne.layers.DropoutLayer(network, p=0.5)
# Наконец, добавим классификатор на 10 классов:
network = lasagne.layers.DenseLayer(
network,
num_units=10,
nonlinearity=lasagne.nonlinearities.softmax)
return networkПолучим вот такую простую полносвязную сеть:
Инициализируем тензорные переменные и скомпилируем Theano-функции для обучения и валидации:
input_var = T.tensor4('inputs')
target_var = T.ivector('targets')
# воспользуемся функцией из предыдущего листинга
network = build_mlp(input_var)
# эта функция вернёт нам граф вычислений, соответствующий сети
prediction = lasagne.layers.get_output(network)
# зададим функцию потерь
loss = lasagne.objectives.categorical_crossentropy(prediction, target_var).mean()
# Сюда также можно добавить L1 или L2 регуляризацию, см. lasagne.regularization.
# Этот метод позволит получить список параметров сети
# он также принимает keyword аргумент, позволяющий выбрать параметры по тегу
# наиболее часто употребимые это trainable и regularizable
params = lasagne.layers.get_all_params(network, trainable=True)
# используем метод стохастического градиентного спуска с моментом Нестерова
updates = lasagne.updates.nesterov_momentum(
loss,
params,
learning_rate=0.01,
momentum=0.9)
# Также создадим выражение для функции потерь на валидации.
# Главное отличие тут заключается в аргументе deterministic=True,
# который отключает dropout
test_prediction = lasagne.layers.get_output(network, deterministic=True)
test_loss = T.nnet.categorical_crossentropy(test_prediction,
target_var).mean()
# Заодно посчитаем точность классификатора
test_acc = T.mean(
T.eq(T.argmax(test_prediction, axis=1), target_var),
dtype=theano.config.floatX)
# скомпилируем функцию для обучения
train = theano.function(
inputs=[input_var, target_var],
outputs=loss,
updates=updates)
# и вторую — для валидации
# оптимизатор Theano тут поймёт, что для вычисления функции потерь и точности
# можно переиспользовать большую часть графа
validate = theano.function(
inputs=[input_var, target_var],
outputs=[test_loss, test_acc])Теперь создадим цикл обучения:
print("| Epoch | Train err | Validation err | Accuracy | Time |")
print("|------------------------------------------------------------------------|")
try:
for epoch in range(100):
# Каждую эпоху будем проходить по всей обучающей выборке
train_err = 0
train_batches = 0
start_time = time.time()
for batch in iterate_minibatches(X_train, y_train, 500, shuffle=True):
inputs, targets = batch
train_err += train(inputs, targets)
train_batches += 1
# И по всей валидационной
val_err = 0
val_acc = 0
val_batches = 0
for batch in iterate_minibatches(X_val, y_val, 500, shuffle=False):
inputs, targets = batch
err, acc = validate(inputs, targets)
val_err += err
val_acc += acc
val_batches += 1
print("|{:05d} | {:4.5f} | {:16.5f} | {:10.2f} | {:7.2f} |".format
(epoch,
train_err / train_batches,
val_err / val_batches,
val_acc / val_batches * 100,
time.time() - start_time))
except KeyboardInterrupt:
print("The training was interrupted on epoch: {}".format(epoch))Получившиеся кривые обучения:

Нашей модели удаётся достичь точности более 98%, что, несомненно, можно улучшить, используя, например, свёрточные нейронные сети, но эта тема уже выходит за рамки данной статьи.
Сохранять и загружать веса удобно с помощью хелперов:
# Сохраняем веса
savez('model.npz', *lasagne.layers.get_all_param_values(network))
network = build_mlp()
# И загружаем, когда потребуется:
with np.load('model.npz') as f:
param_values = [f['arr_%d' % i] for i in range(len(f.files))]
lasagne.layers.set_all_param_values(network, param_values)Документация к Lasagne доступна тут, масса примеров и предобученные модели находятся в отдельном репозитории.
Заключение
В этом посте мы довольно поверхностно ознакомились с возможностями Theano, узнать больше можно:
- обратившись к документации: 1, 2
- посмотрев примеры кода
- пообщавшись с сообществом
- заглянув в исходный код.
Большая благодарность bauchgefuehl за помощь в подготовке поста.
1. Граница между двумя подходами довольно размыта, и не всё сказанное ниже строго верно, всегда есть исключения и пограничные случаи. Наша задача тут — передать основную идею.
2. Разработчики Theano в техническом отчёте и документации называют дифференцирование символьным. Однако, использование этого термина в одной из предыдущих статей на Хабр вызвало обсуждение. Исходя из исходного кода Theano и определения на Википедии, автор считает, что правильный термин всё же «автоматическое дифференцирование».
3. Материал этого раздела по большей части основан на документации к Lasagne.
