Автоматное проектирование. Практикум. Задача «Переправа»
Велосипед изобрести — не речку переплыть. Задача «Переправа» поднималась дважды за пару месяцев, но я хочу отметить вот это решение, поскольку именно оно иллюстрирует удачный предметный взгляд, и даёт модель удачного ОА, которую остаётся только логически развить, что в итоге даст более совершенное решение, чем при иных взглядах на проблему.
Оглавление
Предыдущая статья
Зачастую удачное предметное изображение процесса, который требуется осуществить, равносильно получению решения задачи в общем виде, это чуть ли не половина успеха при выборе ОА. Это настолько важно, что я хочу проиллюстрировать что подразумевается под термином предметный взгляд и то, как из предметного взгляда естественным образом вытекает выбор удачного ОА, а уже выбор удачного ОА сам собой подталкивает к нахождению оптимального решения. Таким образом, можно ставить знак приближённого равенства между выбором оптимального ОА и нахождением оптимального решения. В прошлой статье я продемонстрировал выбор ОА на примере модуля «Дисплей». Дальнейшая работа над «Дисплеем» это уже другая тема: модификация автоматно-реализованных программ, я вернусь к ней чуть позднее. Сегодняшняя задача ещё рельефней показывает процедуру разработки оптимального ОА.
Постановка задачи в виде «волк, коза и капуста» только лишь повод, и речь пойдёт о решении задачи в общем виде, для любого количества участников и их пищевых пристрастий, и любого количества мест в лодках. Задача — получить такой алгоритм, который позволит найти кратчайший путь осуществления переправы, или показать, что задача в такой формулировке не имеет решения.
Тождественные преобразования ТЗ.
Начну с цитаты из предыдущей статьи «бывают случаи, когда предметное изображение условий задачи даже и не намекает, каким операционным автоматом их обрабатывать. В этом случае условия задачи можно подвергнуть математической обработке, и решать не исходную задачу, а математически тождественную, но более удобную».
Если изобразить буквально, процесс перевозки будет состоять из следующих шагов

Рисунок 1. Исходное представление процесса перевозки
Если смотреть на это как математик, и совсем абстрагироваться от логистики речных перевозок, можно увидеть, что шаги 1, 3, 5, 7 излишни. В те моменты, когда крестьянин на берегу, никаких проблем возникнуть не может, рассматривать нужно только случаи когда крестьянин в пути. Случай крестьянина причалившего к берегу означает просто обмен содержимого лодки и берега. Крестьянин в этом случае прочно ассоциируется с лодкой и его можно больше вообще не рассматривать. Поскольку в лодке никаких эксцессов по условию задачи тоже не может произойти, её можно не рассматривать вообще, вместе с содержимым. Если что-то в данный момент находится в лодке, то на берегах будет одним объектом меньше. Всё описанное выше создавало информационный шум, не давая увидеть суть происходящего. В этом случае процесс перевозки изображается так, как показано на рис. 2.
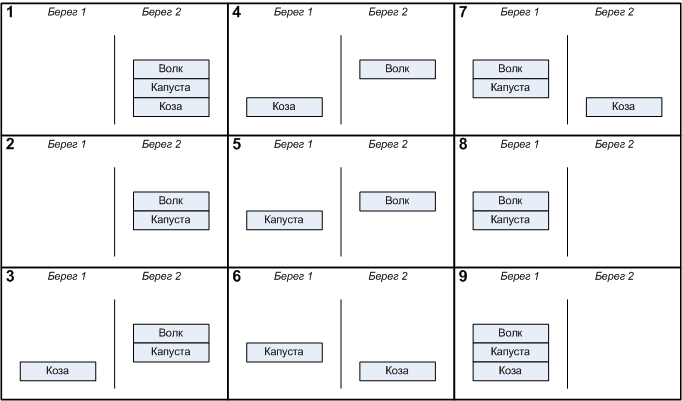
Рисунок 2. Процесс перевозки после тождественных преобразований
То что я сделал это по сути тождественное преобразование. Увидеть тождественность задач показанных на рисунках 1 и 2 помогает математический опыт и математическая интуиция. Не так давно был опрос в котором автор интересовался, нужна ли математика программистам. По моему опыту, для развития математического опыта и интуиции я бы категорически посоветовал программистам изучать теорию вероятностей. Именно теория вероятностей учит и комбинаторике, и тому, что обязательно учитывать не только интересующие варианты (называемые исходы испытаний), но и все возможные варианты. Это фактически подкрепление совета из предыдущей статьи о том, что «важно изображать не только идеальный случай, но и «неудобные» варианты, которые связаны с граничными условиями. … Такой подход смещает ресурсозатраты разработки программы с этапа отладки (когда имеешь дело с кучей реализованных модулей) на этап проектирования (когда имеешь дело с чистым холстом).» В данном случае «удобные» и «неудобные» варианты не являются прямой отсылкой к теории вероятностей, речь идёт о соответствующем образе мышления, который замечательно тренируется упомянутым разделом математики. Это всего лишь совет, можно к нему не прислушиваться, как и к большинству советов в этом мире.
Анализ ТЗ.
Поскольку задача в таком виде, как она изложена выше, довольно избитая, рассмотрим её более сложную модификацию.
Требуется перевезти в лодке с одного берега на другой козу, капусту, собаку и волка. В лодке только два места (одно для крестьянина). Известно, что если оставить волка наедине с собакой, у них будет «вооружённый нейтралитет», однако если с ними останется коза, плотоядная волчья натура взыграет, собака кинется на защиту козы, в общем, втроём их оставлять нельзя. Как осуществить перевозку?
Скажу, что изображение рис. 2 даёт последовательную картину и не даёт наглядности и в этом его главный недостаток. Изобразить задачу в виде таблицы — решение №1, лучшее решение из всех возможных, потому что теперь все исходы событий как на ладони. Строка и столбец, помеченные символом 0, означают пустой берег.
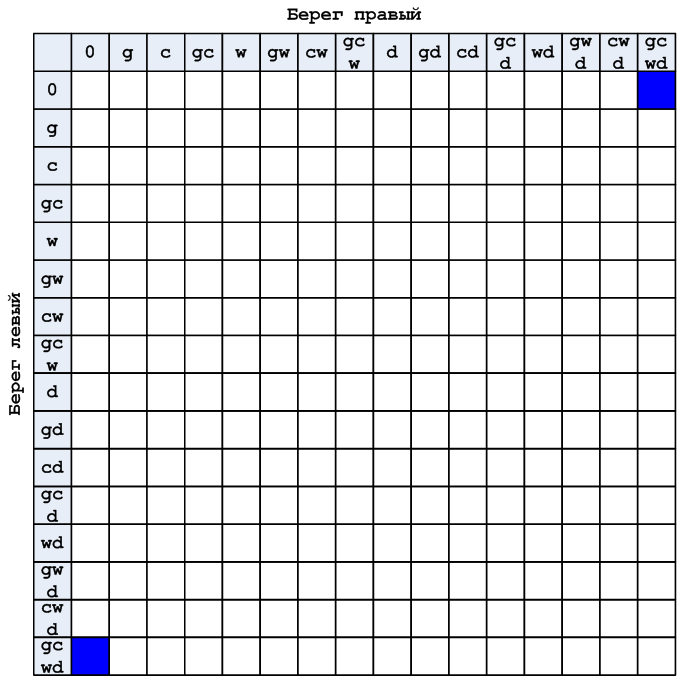
Рисунок 3. Предметное изображение
Это позволяет охватить всю картину целиком, и подключить правое полушарие, которое специализируется на обработке информации, выраженной не в словах, а в символах и образах. Основной сферой специализации правого полушария является интуиция. Конечно, одной интуиции недостаточно, но у «технарей» интуиция не доминирует над логикой, а дополняет её. При правильном подходе правое полушарие (творческое, интуитивное) будет давать пищу для размышлений левому, которое отвечает за логику и анализирует полученные факты. Информация обрабатывается левым полушарием последовательно по этапам. Поскольку весь цикл посвящён программным автоматам, то следующая аналогия укладывается в это русло: правое полушарие можно сравнить с операционным автоматом, который выдаёт решения, а левое полушарие можно сравнить с управляющим автоматом, который испытывает выбранные решения, отсеивает негодные и даёт следующее задание правому, которое «озарением» выдаёт следующую мысль. То есть изображать задачу предметно важно для того, чтобы правое полушарие, охватывающее картину целиком, имело ту пищу для размышлений, которая ему лучше подходит, и это в свою очередь позволит генерировать более релевантные пробные решения, которые станут пищей для размышлений левому полушарию.
Изображение рис. 3 математически тождественно изображению задачи, которое показано на рис. 2, а оно в свою очередь тожественно полному пошаговому изображению процесса с погрузкой и выгрузкой подобного тому, что приведено на рис 1.
При таком изображении задача сводится к нахождению пути из нижнего левого в верхний правый квадрат, которые отмечены синим цветом. Однако не все комбинации (пересечения столбцов и строк) допустимы. Например, комбинация отмеченная крестом, не может существовать, потому что при таком раскладе коза оказывается сразу на двух берегах.
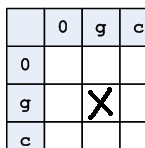
Рисунок 4. Раздваивание персонажей
Если исключить все ситуации связанные с раздваиванием, количество оставшихся вариантов оказывается существенно меньше.
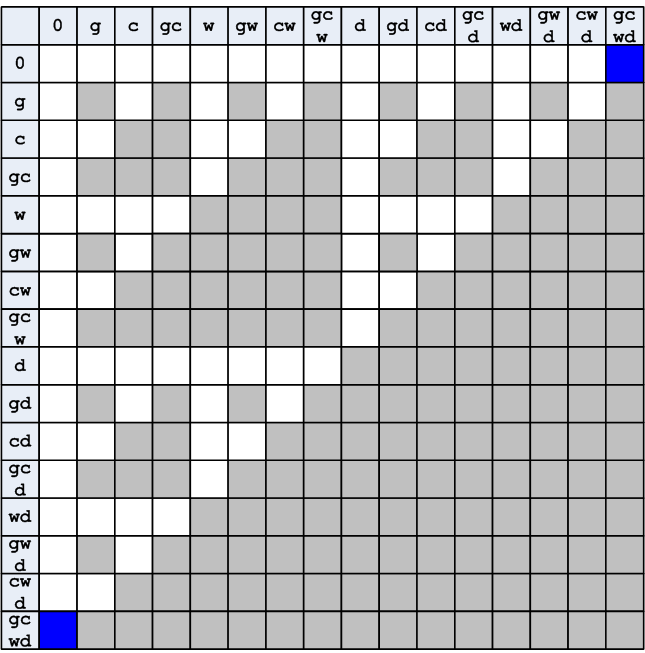
Рисунок 5. Исключение ситуаций с раздваиванием персонажей
Следующий шаг, диктуемой логикой, убрать состояния подобные показанному на рис. 6. Смысл этого в том, что одна коза на левом берегу и никого на правом означает (если исключить то, что волк убежал в лес), что в лодке помимо крестьянина находятся: капуста и волк. Но по условиям задачи в лодке одно место.
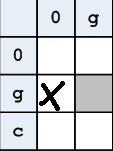
Рисунок 6. Перегруз лодки
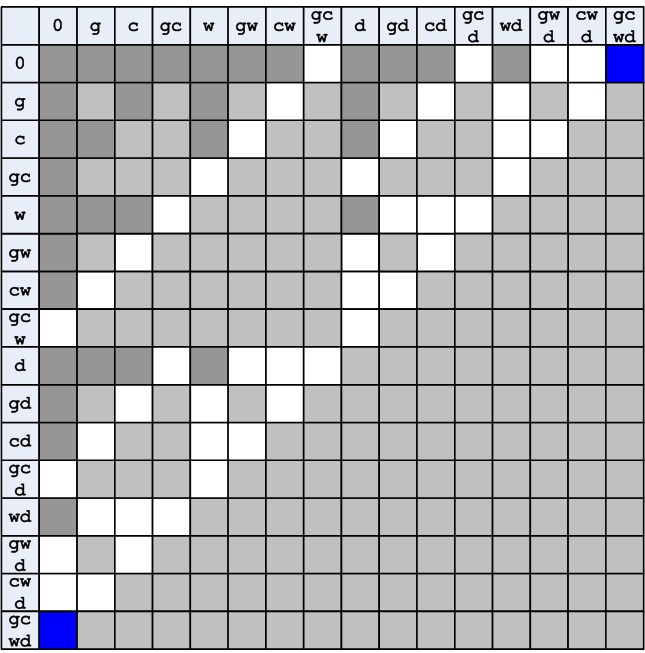
Рисунок 7. Исключение ситуаций с перегрузом лодки
Существуют разновидности этой задачи, когда лодка имеет два пассажирских места. Такие разновидности тождественны решаемому варианту, просто в этом случае будет меньшее количество исключённых по перегрузу ячеек.
Далее требуется исключить все запрещённые ситуации, связанные с поеданием одних персонажей другими.
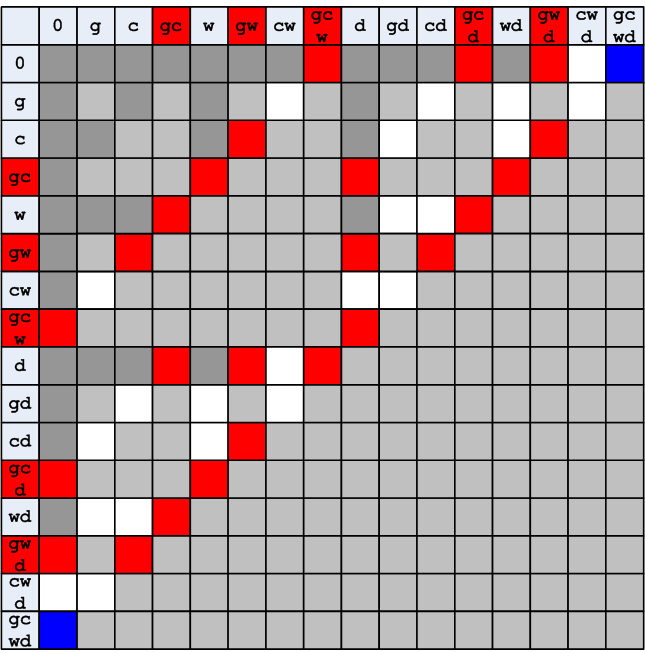
Рисунок 8. Исключение запрещённых состояний
Дальше сокращать количество ячеек невозможно, все оставшиеся состояния — разрешённые. Но как пользоваться этой таблицей?
Можно заметить, что движение вдоль вертикали связано с манипуляциями предметами на левом берегу, а движение по горизонтали, связано с манипуляциями предметами на правом берегу. Например, движение показанное стрелкой означает выгрузку из лодки (на левом берегу) капусты и погрузку волка. Коза на правом берегу.
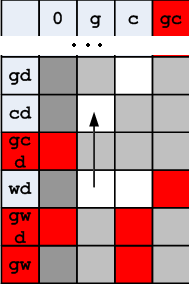
Рисунок 9. Пояснения к манипуляции с предметами
При этом возможно перемещение на любое количество ячеек по горизонтали или вертикали, но не допускается перемещение по диагонали.
Это и есть операционный автомат. Если не воспринимать слово «автомат» буквально, то ОА это способ обработки, схема манипуляции данными, предметами и т.п. В данном случае ОА это таблица, из которой удалены все «невозможные» и недопустимые состояния, по которой можно перемещаться по вертикали или по горизонтали. Теперь осталось только найти кратчайший путь в этом лабиринте, и этим будет заниматься как раз управляющий автомат.
Выражу мысль, что часто программисты рассматривают языки программирования как промежуточный язык, на который требуется перевести исходное ТЗ, написанное на человеческом языке, прежде чем компилятор переведёт его на машинный. Для многих задач такой подход действительно обоснован и естественен, но только тогда, когда манипуляции с ОА описываются очевидной последовательностью действий, например:
1. Считать данные из окна Edit.
2. Преобразовать текст в коэффициенты функции.
3. Вывести график функции на Chart.
Однако в рассматриваемом случае попытка найти решение исходного ТЗ, буквально воплощая условия задачи, привела бы примерно к следующей последовательности действий:
1. Взять очередного персонажа,
2. Перевезти, на другой берег,
3. Если там его оставить нельзя, забрать другого персонажа и вернуть его обратно. перейти к п. 1.
Несмотря на то, что задачу нахождения пути в лабиринте» показанном на рис 8 может выполнить за считанные секунды даже ребёнок вооружённый карандашом, при решении по указанной методике, на каждом этапе могут возникать распараллеливания задачи, поскольку можно взять того или иного персонажа, и для каждого случая будет свой сценарий последующих событий. Такой подход действительно чреват рекурсией с ростом вычислительной сложности.
Пару слов о вычислительной сложности такого решения. Для этой задачи полный перебор это не обход всей таблицы, потому что полный перебор для этой задачи подразумевает не просто перебор всех возможных комбинаций, но всех возможных последовательностей для всех возможных комбинаций.
Управляющий автомат.
Полученная схема предполагает простой алгоритм нахождения пути.
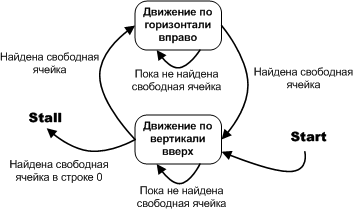
Рисунок 10. Алгоритм поиска пути в лабиринте без тупиков и циклов
Однако, предположительно возможен такой вариант, что потребуется движение вниз или вправо (например при решении этой задачи). Я воспользуюсь своим же советом «рассматривать неудобные случаи».

Рисунок 11. Пример, с необходимостью разнонаправленного движения при обходе свободных ячеек
Чтобы отмести возражения по поводу того, что реальном случае правая нижняя поддиагональная половина должна быть полностью исключена по правилу дублирования персонажей, предположим, что это всего лишь фрагмент из верхней полудиагонали и больше свободных ячеек во всей таблице нет.
Такой лабиринт не обойти, если двигаться всё время вверх или вправо. Очевидно, что здесь нужен серьёзный алгоритм поиска пути. Поиск пути «в лоб» для варианта рис. 11 приведёт к перебору всех возможных путей, и хотя количество комбинаций сравнительно невелико, это чревато опять же рекурсией и имеет те же недостатки, что и вариант полного перебора. Лучше воспользоваться т.н. волновым алгоритмом или алгоритмом Ли. Не буду его здесь описывать, можно бегло поглядеть по ссылке.
Вернёмся, однако, к переправе, рис. 8. Распространение волны начинается с верхнего правого угла, которому присвоено число 0. Обратите внимание, поиск по вертикали вниз для этого столбца невозможен, поскольку все клетки в этом столбце исключены по правилу дублирования. Единственное возможное движение — влево. В строке только одна «белая» клетка. Помечаем её цифрой 1. После этого таким же способом помечается клетка 2.
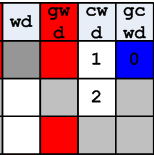
Рисунок 12. Первые два шага расчёта волны.
Далее важный момент. Из клетки, помеченной 2, можно переместиться в любую из клеток по горизонтали за один ход, все они должны быть помечены цифрой 3.

Рисунок 13. Эквивалентные клетки
Последовательное применение указанного алгоритма даёт в результате следующую картину.
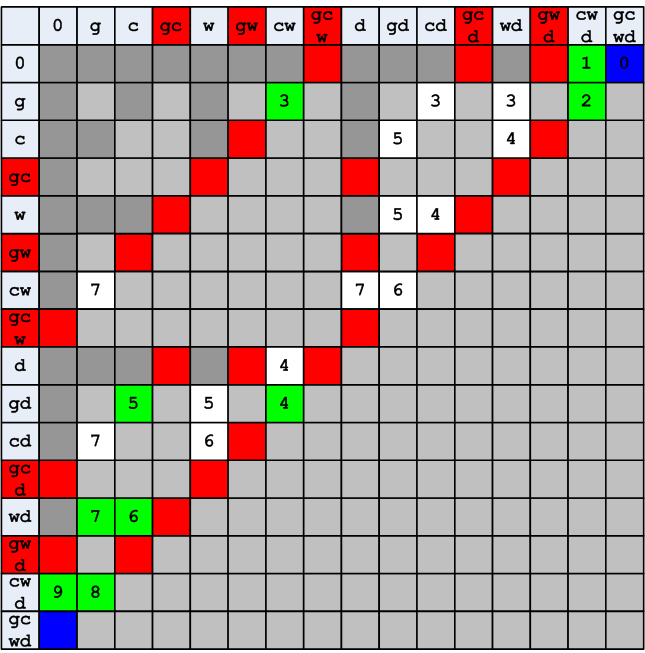
Рисунок 14. Размеченное поле для поиска кратчайшего пути, и найденный путь (зелёные клетки)
Критерий успешного окончания поиска — в вертикали с индексом 0 должна быть хоть одна «незабракованная» клетка, и она должна быть помечена цифрой. Поиск пути ведётся классическим способом: находясь в каждой клетке ищется соседняя клетка (в нашем случае любая в той же строке или в том же столбце), у которой число меньше. Зелёным цветом выделены клетки, составляющие путь.
Воспользовавшись своим же советом рассматривать неудобные варианты, предлагаю рассмотреть иллюстрацию
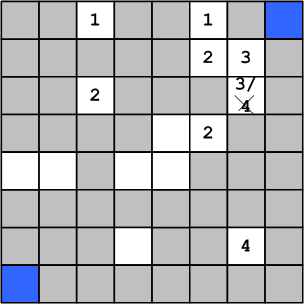
Рисунок 15. Неоднозначность
В этом случае кажется, что при обходе лабиринта разными путями, возникает противоречие. Однако, на самом деле противоречия нет, достаточно ставить цифры только в ещё не занятые ячейки. Тогда при обходе пути который привёл бы к значению 4, спорная ячейка уже содержит 3 и просто не попадает в рассмотрение.
Один из вариантов построения волны предполагает рекурсивный характер алгоритма перебора точек. Однако, я предлагаю другое решение. Оно позволяет обойтись без рекурсии, и основано на следующем рацпредложении.
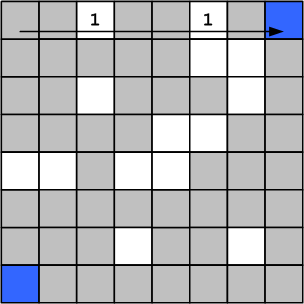
Рисунок 16. Расчёт волны шаг 1
Расчёт волны будет состоять из поочерёдного обхода строк и обхода столбцов. Рассмотрение начинается с верхней строки, во все ячейки которой ставятся 1. Далее строка обходится повторно (этап «поиск»), и для каждой ячейки, содержащей 1 проводится цикл вниз по столбцу (этап «сканирование-заполнение»), в ходе которого все свободные ячейки помечаются числом на 1 большим, чем предыдущее.
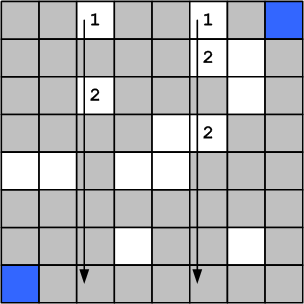
Рисунок 17. Расчёт волны шаг 2
После этого столбцы и строки меняются местами, и теперь ведётся поиск столбцов содержащих число 2, и из каждого столбца производится сканирование-заполнение соответствующей строки.

Рисунок 18. Расчёт волны шаг 3
Указанная операция повторяется до тех пор, пока не будет отмечена хоть одна ячейка в столбце 0. Учитывая то, что пути обхода может не быть вовсе, обход прекращается в том случае, если при очередном обходе (поиск + сканирование-заполнение) не найдено ни одной новой ячейки.

Рисунок 19. Результат построения волны
При таком обходе каждая строка проходится по 2 раза — во время поиска и во время сканирования-заполнения. Точнее, поскольку после просмотра по горизонтали начинается сканирование по вертикали, будет правильнее перечислить в другом порядке: во время сканирования-заполнения и во время последующего поиска.
Но поскольку на момент каждой итерации неизвестно, какая строка содержит число, например 3, а какая не содержит его, для поиска каждой строки нужно просмотреть все строки, и это приводит к тому, что каждая строка просматривается один раз во время поиска числа 3 и ещё много раз при поиске остальных чисел (которых там нет).
Обращаю внимание, что итерации «поиск + сканирование-заполнение» чередуются для строк и столбцов, поэтому во время поиска по строкам, не будут искаться чётные, и соответственно наоборот. В этом случае количество просмотров каждой ячейки сокращается вдвое.
Но, обратите внимание на одну характерную вещь. В силу алгоритма заполнения каждая строка будет иметь вид.
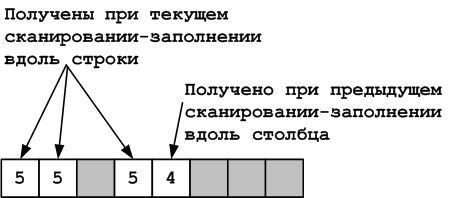
Рисунок 20. Типичное содержимое строки
Обращаю внимание, что алгоритм не рекурсивный. Если бы он был рекурсивный, это означало бы, что исследуется на максимальную глубину один путь, после чего алгоритм возвращается назад (на одну позицию за раз, но может получится так, что до самого начала), после чего исследуется следующий путь. В результате такого характера обхода, добавление чисел в таблицу идёт не в возрастающем порядке, но младшие числа могут добавляться на поле, в котором уже полно старших.
При обходе таблицы способом, описанным выше, каждая строка будет содержать число
N-1 полученное при сканировании-заполнении предыдущей итерации, и числа N которые будут занесены в неё при сканировании-заполнении текущей итерации. Причём чисел N-1 может оказаться несколько, в силу того, что каждая итерация подразумевает сканирование-заполнение ряда линий, но в строке не будет ни одного числа отличного от N-1, N.
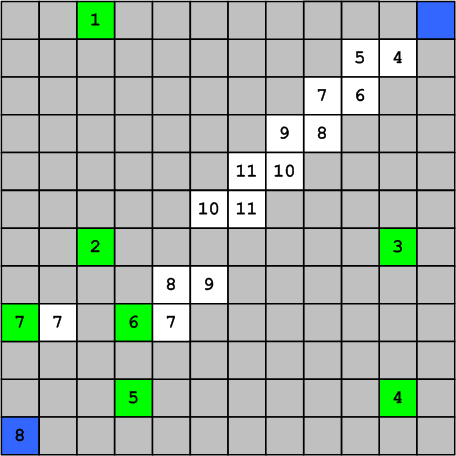
Рисунок 21. Иллюстрация особенности заполнения строк и столбцов
Более того, в случае рис. 20 число 4 относятся не к строке, а к столбцу, таким образом, если рассматривать только числа относящиеся к строке, получается что строка содержит только числа 5. Со столбцами ситуация аналогичная.
Это больше чем просто наблюдение это основание для дальнейшей разработки. Проиллюстрированный рис. 16–19 алгоритм подразумевает предварительный просмотр ячеек каждой строки, с целью определить содержит ли она искомое число (например, для рис. 21 возьмём поиск числа 7). Учитывая то, что строки содержат пару чисел N-1 и N просмотр первой строки можно прекратить, дойдя до ячейки с единицей. Вторую строку тоже можно не рассматривать до конца, встретив число 5, но её уже придётся прокручивать почти до конца. В то же время, поскольку, как я показал, с каждой заполненной строкой ассоциировано только одно число, и с каждым столбцом тоже одно число, можно интерпретировать задачу следующим образом. В дополнение к таблице создаётся пара массивов — один для строк и один для столбцов.
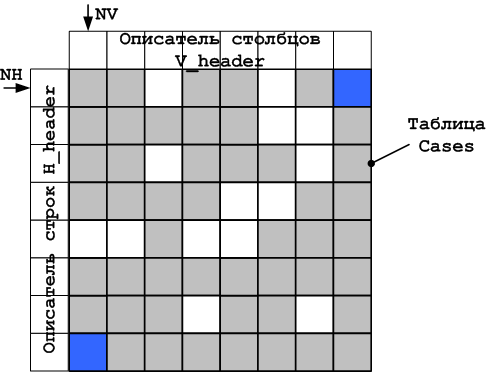
Рисунок 22. ОА построения волны
Поскольку из правого верхнего синего квадрата можно двигаться только по горизонтали (вся вертикаль исключена по правилу дублирования) поиск начинается со строки, отмеченной стрелкой NH. В ячейку H_header[0] заносится 1 ещё при инициализации. Далее следует процедура, которую можно описать диаграммой состояний показанной на рис. 23
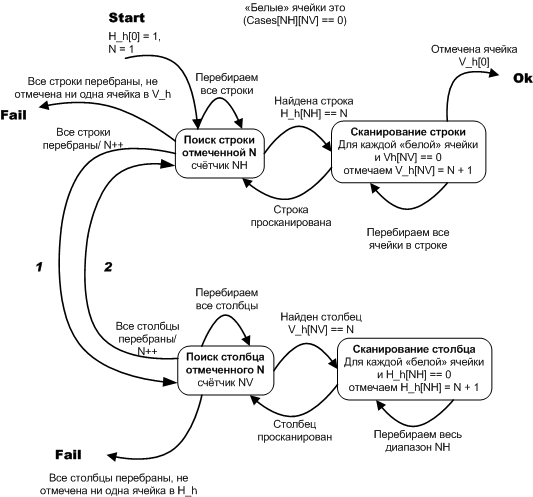
Рисунок 23. Алгоритм построения волны
Почему я считаю, что диаграмма состояний это альтернативная, более удобная форма записи программных алгоритмов? Она — удобный инструментом «стенографирования» мыслей, по мере того как они приходят в голову, поскольку построена из идентичных блоков, которые можно соединять любыми вообразимыми линиями.
Как по такой диаграмме создать алгоритм? В общем-то элементарно, даже проще и механистичней, чем если бы я описал всё словами. Те действия которые помечены как перебираем…, соответствуют циклам, остальные стрелки условиям, стрелки слева, помеченные 1 и 2 подразумевают цикл while(1) .
uint tCalculator::Make_wave()
{
u1x N = 1;
Horizontals_header[0] = 1;
while(1)
{
////////////////////////////
// Поиск горизонтали
bool Found = false;
for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++)
{
if(Horizontals_header[Horizontal_N] == N)
{
////////////////////////////
// Сканирование найденной горизонтали
for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++)
{
if( (Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) &&
(Verticals_header[Vertical_N] == 0 ) )
{
Found = true;
Verticals_header[Vertical_N] = N + 1;
if( Vertical_N == 0 )
return(N+1);
}
}//for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++)
}//if(Horizontals_header[Horizontal_N] == N)
}//for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++)
if(!Found)
return(0);
Found = false;
N++;
////////////////////////////
// Поиск вертикали
for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++)
{
if(Verticals_header[Vertical_N] == N)
{
////////////////////////////
// Сканирование найденной вертикали
for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++)
{
if( (Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) &&
(Horizontals_header[Horizontal_N] == 0 ) )
{
Found = true;
Horizontals_header[Horizontal_N] = N + 1;
if( Horizontal_N == Line_size - 1 )
return(N+1);
}
}//for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++)
}//if(Verticals_header[Vertical_N] == N)
}//for(u1x Vertical_N = 0; Vertical_N < Line_size; Vertical_N++)
if(!Found)
return(0);
N++;
}//while(1)
}//uint tCalculator::Make_wave()Результат работы алгоритма показан на рис 24. В саму таблицу никакие пометки не заносятся. Кроме того, для удобства метод Make_wave возвращает число, начиная с которого ведётся построение трассы, в данном случае — 10.
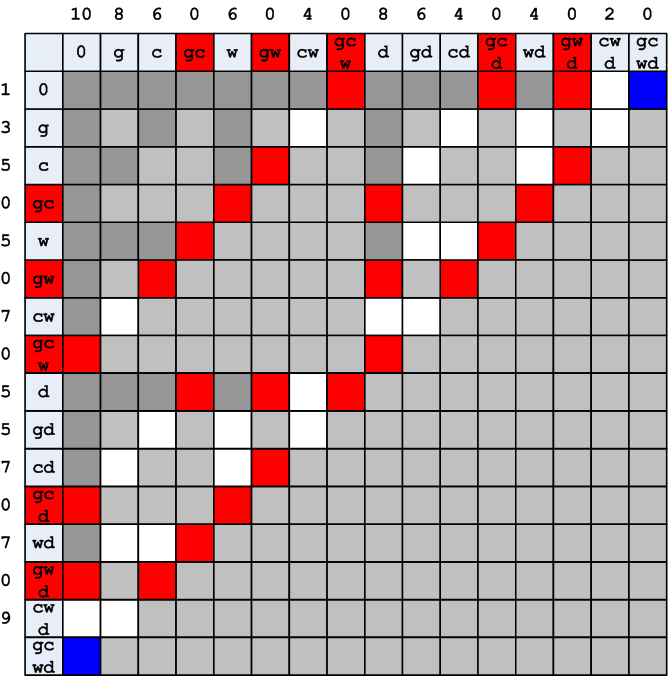
Рисунок 24. Построенная волна
После того, как получена волна, строится трасса. Алгоритм построения трассы можно описать диаграммой состояний.
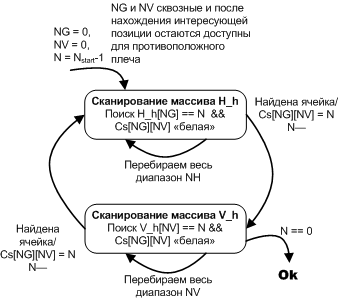
Рисунок 25. Алгоритм построения трассы
////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////
////////////////////////////////////////////////////////////////////////////////
void tCalculator::Make_trace(u1x N)
{
u1x Horizontal_N = 0;
u1x Vertical_N = 0;
while(1)
{
//////////////////////////////
// Сканирование массива Horizontals_header
// В силу алгоритма N всегда чётное и выход из алгоритма в другом плече
N--;
for(Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++)
{
if((Horizontals_header[Horizontal_N] == N)&&(Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) )
{
Cases_table[Horizontal_N * Line_size + Vertical_N] = N;
break;
}
}//for(u1x Horizontal_N = 0; Horizontal_N < Line_size; Horizontal_N++)
N--;
if(!N)
return;
//////////////////////////////
// Сканирование массива Verticals_header
for(Vertical_N = 0; Vertical_N < Line_size; Vertical_N++)
{
if( ( Verticals_header[Vertical_N] == N) && (Cases_table[Horizontal_N * Line_size + Vertical_N] == 0) )
{
Cases_table[Horizontal_N * Line_size + Vertical_N] = N;
break;
}
}//for(Vertical_N = 0; Vertical_N < Line_size; Vertical_N++)
}//while(1)
}//void tCalculator::Make_trace()Сам проект можно увидеть на bitbucket.
Модуль Table_calculator содержит описание класса tCalculator, который и несёт весь функционал.
Программа
Пару слов о путях дальнейшего усовершенствования описанной программы. Рассмотрим задачу:
Вам нужно перевезти в лодке с одного берега на другой козу, капусту, собаку и двух волков. В лодке только три места (одно для крестьянина). Известно, что волка нельзя оставлять без присмотра с козой и с собакой, собаку нельзя оставлять с козой и, разумеется, коза неравнодушна к капусте. Как осуществить перевозку?
В таком виде для поиска решения задачи с помощью описанной программы, придётся одного из волков обозначить буквой w, а другого W, потому что парсеримён персонажей игнорирует повторы имён. Соответственно правила запрета нужно задавать как wd, Wd.
Относительно несложно сделать так, чтобы можно было решать задачу для произвольного количества одноимённых участников, перечисляя их в виде 2w,3g,5c и задавать правила запрета в простом виде wd для любого волка, или g5c (запрет оставлять козу наедине с 5 мешками капусты, а то съест за раз и помрёт), однако разница будет в деталях, а суть решения останется прежней. Поэтому я пока не стану делать этого.
В заключение добавлю, что ранее я показывал процесс практической декомпозиции как.
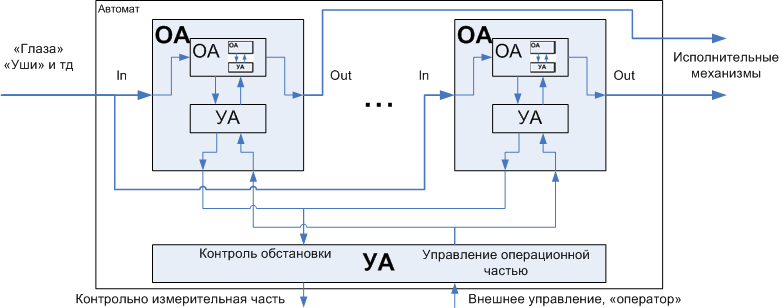
Рисунок 26. Многоуровневая декомпозиция автоматов
Рассмотренный сегодня вариант, это тоже пример декомпозиции, но другого рода — конвейер операционных автоматов.
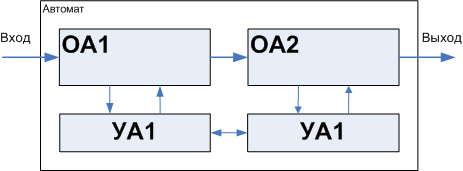
Рисунок 27. Конвейерная декомпозиция автоматов
Поскольку выбор ОА так важен, я буду приводить ещё примеры решения задач автоматным проектированием. На сегодня всё.
