Автоматическая оптимизация алгоритмов с помощью быстрого возведения матриц в степень в Python15.09.2014 17:18

Пусть мы хотим вычислить десятимиллионное число Фибоначчи программой на Python. Функция, использующая тривиальный алгоритм, на моём компьютере будет производить вычисления более 25 минут. Но если применить к функции специальный оптимизирующий декоратор, функция вычислит ответ всего за 18 секунд (в 85 раз быстрее): Дело в том, что перед выполнением программы интерпретатор Python компилирует все её части в специальный байт-код. Используя метод, описанный хабрапользователем SkidanovAlex, данный декоратор анализирует получившийся байт-код функции и пытается оптимизировать применяющийся там алгоритм. Далее вы увидите, что эта оптимизация может ускорять программу не в определённое количество раз, а асимптотически. Так, чем больше будет количество итераций в цикле, тем в большее количество раз ускорится оптимизированная функция по сравнению с исходной.Эта статья расскажет о том, в каких случаях и каким образом декоратору удаётся делать подобные оптимизации. Также вы сможете сами скачать и протестировать библиотеку cpmoptimize, содержащую данный декоратор.

Теория Два года назад SkidanovAlex опубликовал интересную статью с описанием интерпретатора ограниченного языка, который поддерживает следующие операции: # Присвоить переменной другую переменную или константу x = y x = 1

# Сложить или вычесть из переменной другую переменную или константу x += y x += 2 x -= y x -= 3

# Умножить переменную на константу x *= 4

# Запустить цикл с константным числом итераций loop 100000 … end Значения переменных в языке должны быть числами, их размер не ограничен (поддерживается длинная арифметика). На самом деле переменные хранятся как целые числа в Python, который переключается в режим длинной арифметики, если число выходит за границы аппаратно поддерживаемого четырёх- или восьмибайтового типа.Рассмотрим случай, когда длинная арифметика не используется. Тогда время выполнения операций не будет зависеть от значений переменных, а значит в цикле все итерации будут выполняться за одинаковое время. Если выполнять такой код «в лоб», как в обычных интерпретаторах, цикл выполнится за время 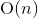, где n — количество итераций. Другими словами, если код для n итераций работает за время t, то код для  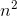итераций будет работать за время 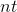(см. сложность вычислений).

Интерпретатор из оригинальной статьи представляет каждую поддерживаемую языком операцию с переменными в виде определённой матрицы, на которую умножается вектор с исходными значениями переменных. В результате умножения мы получаем вектор с новыми значениями переменных:

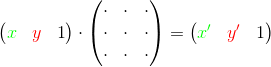
Таким образом, для выполнения последовательности операций нужно по очереди домножать вектор на матрицу, соответствующую очередной операции. Другой способ — пользуясь ассоциативностью, матрицы можно сперва умножить друг на друга, а потом умножить исходный вектор на получившееся произведение:

Для выполнения цикла мы должны вычислить число n — количество итераций в цикле, а также матрицу B — последовательное произведение матриц, соответствующих операциям из тела цикла. Затем нужно n раз умножить исходный вектор на матрицу B. Другой способ — можно сначала возвести матрицу B в степень n, а потом умножить вектор с переменными на результат:

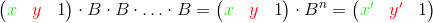
Если при этом использовать алгоритм бинарного возведения в степень, цикл можно будет выполнить за значительно меньшее время 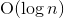. Так, если код для n итераций работает за время t, то код для  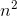итераций будет работать за время 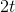(всего лишь в два раза медленнее, а не в n раз медленнее, как в предыдущем случае).

В итоге, как и было написано выше, чем больше будет количество итераций в цикле n, тем в большее количество раз ускоряется оптимизированная функция. Поэтому эффект от оптимизации будет особенно хорошо заметен для больших n.

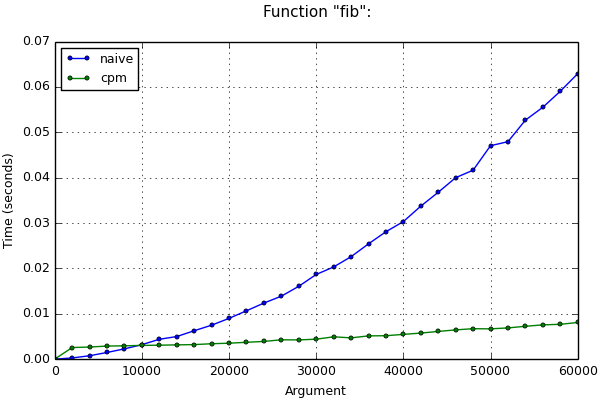
Если длинная арифметика всё-таки используется, оценки времени выше могут быть неверны. Например, при вычислении n-го числа Фибоначчи значения переменных из итерации в итерацию становятся всё больше, и операции с ними замедляются. Асимптотическую оценку времени работы программы в таком случае сделать сложнее (нужно учитывать длину чисел в переменных на каждой итерации и используемые методы перемножения чисел) и здесь она приведена не будет. Тем не менее, после применения данного метода оптимизации асимптотика улучшается даже в таком случае. Это хорошо заметно на графике:

Идея Если десятки лет назад программисту потребовалось бы умножить переменную в программе на 4, он использовал бы не операцию умножения, а её более быстрый эквивалент — битовый сдвиг влево на 2. Теперь компиляторы сами умеют делать подобные оптимизации. В борьбе за сокращение времени разработки появились языки с высоким уровнем абстракции, новые удобные технологии и библиотеки. При написании программ всё большую часть своего времени разработчики тратят на объяснение компьютеру того, что должна сделать программа (умножить число на 4), а не того, как ей это сделать эффективно (использовать битовый сдвиг). Таким образом, задача создания эффективного кода частично переносится на компиляторы и интерпретаторы.Сейчас компиляторы умеют заменять различные операции на более эффективные, предсказывать значения выражений, удалять или менять местами части кода. Но компиляторы ещё не заменяют сам алгоритм вычислений, написанный человеком, на асимптотически более эффективный.

Реализацию описываемого метода, представленную в оригинальной статье, проблематично использовать в реальных программах, так как для этого придётся переписать часть кода на специальный язык, а для взаимодействия с этим кодом придётся запускать сторонний скрипт с интерпретатором. Однако, автор статьи предлагает использовать свои наработки на практике в оптимизирующих компиляторах. Я попытался реализовать данный метод для оптимизации программ на Python в виде, действительно пригодном для использования в реальных проектах.

Если использовать написанную мной библиотеку, для применения оптимизации достаточно будет дописать перед функцией, которую нужно ускорить, одну строчку с применением специального декоратора. Этот декоратор самостоятельно оптимизирует циклы, если это возможно, и ни при каких обстоятельствах не «ломает» программу.

Примеры использования Рассмотрим ряд задач, в которых может пригодиться наш декоратор.Пример №1. Длинные циклы Пусть у нас есть некоторая последовательность, соответствующая правилу, изображённому на схеме, и нам нужно вычислить её n-ый член: 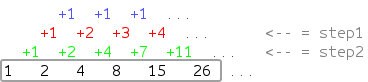В таком случае интуитивно понятно, как появляется очередной член последовательности, однако требуется время, чтобы придумать и доказать соответствующую ему математическую формулу. Тем не менее, мы можем написать тривиальный алгоритм, описывающий наше правило, и предложить компьютеру самому придумать, как быстро считать ответ на нашу задачу: from cpmoptimize import cpmoptimize, xrange

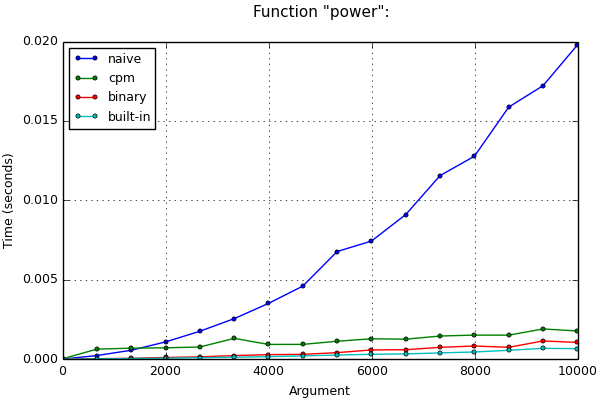
@cpmoptimize () def f (n): step1 = 1 step2 = 1 res = 1 for i in xrange (n): res += step2 step2 += step1 step1 += 1 return res Интересно, что если запустить эту функцию для 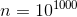, внутри будет запущен цикл с  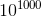итераций. Без оптимизации такая функция не закончила бы работать ни за какой мыслимый промежуток времени, но с декоратором она выполняется меньше секунды, возвращая при этом правильный результат.Пример №2. Числа Фибоначчи Для быстрого вычисления n-го числа Фибоначчи есть быстрый, но нетривиальный алгоритм, основанный на той же идее о возведении матриц в степень. Опытный разработчик может реализовать его за несколько минут. Если коду, где производятся подобные вычисления, не нужно работать быстро (например, если необходимо однократно вычислить число Фибоначчи с номером, меньшим 10 тысяч), для экономии своего рабочего времени разработчик, скорее всего, решит сэкономить усилия и за несколько секунд написать решение «в лоб».Если программа всё-таки должна работать быстро, либо придётся приложить усилия и написать сложный алгоритм, либо же можно воспользоваться методом автоматической оптимизации, применив к функции наш декоратор. Если n достаточно велико, в обоих случаях производительность программ получится почти одинаковой, но во втором случае разработчик потратит меньше своего рабочего времени.

Вы можете сравнить время работы описанных методов ниже по таблицам и графикам для малых и для больших n.

Справедливости ради следует отметить, что для вычисления чисел Фибоначчи есть ещё один алгоритм, известный как fast doubling. Он несколько выигрывает предыдущие алгоритмы по времени, так как в нём исключены лишние сложения и умножения чисел. Время вычислений через этот алгоритм также представлено на графиках для сравнения.

Графики Результаты измерений времени Function «fib»:

(*) Testcase «big»: ±-------±---------±-------------±-------------±-------------±------+ | arg | naive, s | cpm, s | matrixes, s | fast dbl, s | match | ±-------±---------±-------------±-------------±-------------±------+ | 0×0.00×0.00×0.00×0.00 | True | | 20000×0.01×0.00 (2.5x) | 0.00 (3.0x) | 0.00 (5.3x) | True | | 40000×0.03×0.01 (5.8x) | 0.00 (1.8x) | 0.00 (4.9x) | True | | 60000×0.07×0.01 (7.7x) | 0.01 (1.4x) | 0.00 (4.8x) | True | | 80000×0.11×0.01 (9.6x) | 0.01 (1.3x) | 0.00 (4.6x) | True | | 100000×0.16×0.01 (11.7x) | 0.01 (1.2x) | 0.00 (4.3x) | True | | 120000×0.24×0.02 (11.6x) | 0.02 (1.2x) | 0.00 (5.0x) | True | | 140000×0.31×0.02 (14.6x) | 0.02 (1.1x) | 0.00 (4.1x) | True | | 160000×0.40×0.03 (13.8x) | 0.03 (1.1x) | 0.01 (4.2x) | True | | 180000×0.51×0.04 (14.2x) | 0.03 (1.1x) | 0.01 (4.3x) | True | | 200000×0.63×0.04 (15.9x) | 0.04 (1.1x) | 0.01 (4.6x) | True | | 220000×0.78×0.05 (16.1x) | 0.04 (1.1x) | 0.01 (4.8x) | True | | 240000×0.90×0.05 (16.6x) | 0.05 (1.1x) | 0.01 (4.8x) | True | | 260000×1.07×0.06 (17.3x) | 0.06 (1.1x) | 0.01 (4.6x) | True | | 280000×1.26×0.06 (21.4x) | 0.06 (1.1x) | 0.01 (4.1x) | True | | 300000×1.41×0.07 (19.2x) | 0.07 (1.1x) | 0.02 (4.4x) | True | ±-------±---------±-------------±-------------±-------------±------+ На практике мы можем встретится с более сложной ситуацией, если последовательность чисел вместо известной рекуррентной формулы: 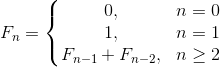Задаётся несколько усложнённой формулой, например, такой:

В таком случае мы не сможем найти реализацию вышеописанных алгоритмов в Интернете, а на то, чтобы вручную придумать алгоритм с возведением матриц в степень, уйдёт существенное время. Тем не менее, мы можем написать решение «в лоб» и применить декоратор, тогда компьютер придумает быстрый алгоритм за нас:

from cpmoptimize import cpmoptimize

@cpmoptimize () def f (n): prev3 = 0 prev2 = 1 prev1 = 1 for i in xrange (3, n + 3): cur = 7 * (2 * prev1 + 3 * prev2) + 4 * prev3 + 5 * i + 6 prev3, prev2, prev1 = prev2, prev1, cur return prev3 Пример №3. Сумма геометрической прогрессии Пусть нам необходимо вычислить сумму count членов геометрической прогрессии, для которой задан первый член start и знаменатель coeff. В данной задаче декоратор снова способен оптимизировать наше тривиальное решение: from cpmoptimize import cpmoptimize

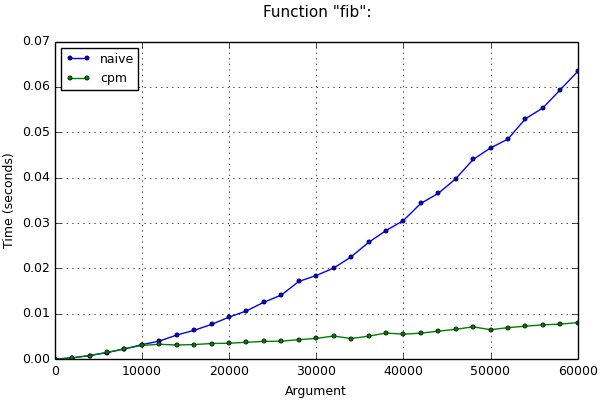
@cpmoptimize () def geom_sum (start, coeff, count): res = 0 elem = start for i in xrange (count): res += elem elem *= coeff return res График Пример №4. Возведение в степень Пусть нам необходимо возвести число a в неотрицательную целую степень n. В такой задаче декоратор фактически будет заменять тривиальное решение на алгоритм бинарного возведения в степень: from cpmoptimize import cpmoptimize

@cpmoptimize () def power (a, n): res = 1 for i in xrange (n): res *= a return res График Ссылки для скачивания Установить библиотеку можно с помощью pip: sudo pip install https://github.com/borzunov/cpmoptimize/archive/v0.1.tar.gz Исходный код библиотеки с примерами доступен на github под свободной лицензией MIT.Примеры применения оптимизации находятся в папке «tests/». Каждый пример состоит из функции, представляющей решение «в лоб», её оптимизированного варианта, а также функций, представляющих известные сложные, но быстрые решения данной задачи. Эти функции помещены в скрипты, которые запускают их на различных группах тестов, замеряют время их работы и строят соответствующие таблицы. Если установлена библиотека matplotlib, скрипты также будут строить графики зависимости времени работы функций от входных данных (обычные или логарифмические) и сохранять их в папку «tests/plots/».

Описание библиотеки При создании библиотеки я воспользовался тем, что байт-код программы, который создаёт интерпретатор Python, на этапе выполнения можно анализировать и изменять без вмешательства в интерпретатор, что даёт широкие возможности по расширению языка (см., например, реализация конструкции goto). Преимущества описываемого метода обычно проявляются при использовании длинной арифметики, которая также встроена в Python.По этим причинам реализация описываемой оптимизации в Python стала для меня более интересной задачей, хотя, конечно, её применение в компиляторах C++ позволило бы создавать ещё более быстрые программы. К тому же, оптимизированный декоратором код на Python, как правило, обгоняет код «в лоб» на C++ благодаря более хорошей асимптотике.

При модификации байт-кода я использовал модуль byteplay, предоставляющий удобный интерфейс для дизассемблирования и ассемблирования байт-кода. К сожалению, модуль ещё не был портирован на Python 3, поэтому весь проект я реализовывал на Python 2.7.

Название библиотеки cpmoptimize является сокращением от слов «compute the power of a matrix and optimize». Объём статьи не позволяет подробно рассказать о процессе анализа и модификации байт-кода, однако я постараюсь подробно описать, какие возможности предоставляет данная библиотека и на каких принципах основана её работа.

Собственный xrange cpmoptimize.xrange (stop)cpmoptimize.xrange (start, stop[, step])Встроенный тип xrange в Python 2 в целях оптимизации не поддерживает длинные целые типа long в качестве аргументов:

>>> xrange (10 ** 1000) Traceback (most recent call last): File »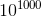», line 1, in OverflowError: Python int too large to convert to C long Так как при использовании нашей библиотеки циклы с количеством операций порядка могут выполняться менее, чем за секунду, и стать в программе обычным делом, библиотека предоставляет собственную реализацию типа xrange на чистом Python (внутри библиотеки она называется CPMRange). Она поддерживает все возможности обычного xrange и, кроме того, аргументы типа long. Такой код не приведёт к ошибкам и быстро вычислит правильный результат: from cpmoptimize import cpmoptimize, xrange

@cpmoptimize () def f (): res = 0 for i in xrange (10 ** 1000): res += 3 return res

print f () Тем не менее, если в вашем случае количество итераций в циклах невелико, вы можете продолжать использовать вместе с декоратором встроенный xrange.Функция cpmoptimize cpmoptimize.cpmoptimize (strict=False, iters_limit=5000, types=(int, long), opt_min_rows=True, opt_clear_stack=True)Применение декоратора Функция cpmoptimize принимает параметры производимой оптимизации и возвращает декоратор, учитывающий эти параметры, который и нужно применить к оптимизируемой функции. Это можно сделать, используя специальный синтаксис (с символом «собака») или без него: from cpmoptimize import cpmoptimize

@cpmoptimize () def f (n): # Некоторый код

def naive_g (n): # Некоторый код

smart_g = cpmoptimize ()(naive_g) Перед внесением изменений в байт-код исходная функция копируется. Таким образом, в коде выше функции f и smart_g в итоге окажутся оптимизированными, а naive_g — нет.Поиск циклов for Декоратор ищет в байт-коде функции стандартные циклы for, при этом циклы while и циклы for внутри генераторных и списковых выражений игнорируются. Вложенные циклы пока не поддерживаются (оптимизируется только самый внутренний цикл). Корректно обрабатываются конструкции for-else.Допустимые типы Декоратор не может оптимизировать цикл независимо от того, какие типы переменных используются в нём. Дело в том, что, например, Python позволяет определить тип, который при каждом умножении записывает строку в файл. В результате применения оптимизации количество сделанных в функции умножений могло бы измениться. Из-за этого количество строк в файле стало бы другим и оптимизация бы сломала программу.Кроме того, при операциях с матрицами переменные складываются и умножаются неявным образом, потому типы переменных могут «перемешиваться». Если одна из констант или переменных имела бы тип float, те переменные, которые должны были бы после выполнения кода иметь тип int, могли бы тоже получить тип float (так как сложение int и float возвращает float). Такое поведение может вызвать ошибки в программе и также неприемлемо.

Чтобы избежать нежелательных побочных эффектов, декоратор оптимизирует цикл, только если все константы и переменные, используемые в нём, имеют допустимый тип. Изначально допустимыми типами являются int и long, а также унаследованные от них типы. Если одна из констант или переменных имеет тип long, те переменные, которые должны были бы после выполнения кода иметь тип int, могут тоже получить тип long. Однако, так как int и long в Python в достаточной степени взаимозаменяемы, это не должно приводить к ошибкам.

В случае, если вы хотите изменить набор допустимых типов (например, чтобы добавить поддержку float), вы должны передать кортеж из нужных типов в параметре types. Типы, входящие в этот кортеж или унаследованные от типов, входящих в этот кортеж, будут считаться допустимыми. На деле проверка того, что какое-либо значение value имеет допустимый тип, будет осуществляться с помощью выражения isinstance (value, types).

Условия оптимизации цикла Каждый найденный цикл должен удовлетворять ряду условий. Часть из них проверяется уже при применении декоратора: Тело цикла должно состоять только из инструкций присваивания, унарных и бинарных операций, которые могут быть скомпонованы в сложные выражения. Оно не может содержать условий, вызовов других функций, операторов return и yield и т. д… От операндов может требоваться условие предсказуемости: на каждой итерации цикла их значение должно быть одним и тем же, причём оно не должно зависеть от результатов каких-либо вычислений на предыдущей итерации. При этом: Все операнды сложения и вычитания, а также операнд унарного минуса могут быть непредсказуемыми. Хотя бы один операнд умножения должен быть предсказуем (аналогично тому, что в оригинальном интерпретаторе поддерживалось только умножение на константу). Все операнды возведения в степень, операций деления и взятия остатка и побитовых операций должны быть предсказуемы. Все константы, используемые в цикле, должны иметь допустимый тип. Если эти условия выполняются, перед циклом устанавливается «ловушка», которая проверит другую часть условий, при этом оригинальный байт-код цикла не удаляется. Так как в Python используется динамическая типизация, следующие условия могут быть проверены только непосредственно перед запуском цикла: Объект, по которому проходится цикл, должен иметь стандартный тип xrange или его аналог из данной библиотеки cpmoptimize.xrange. При этом медленная функция range, возвращающая список, не поддерживается. Значения всех переменных, используемых в цикле, имеют допустимый тип. Если «ловушка» заключила, что оптимизация приемлема, будут рассчитаны необходимые матрицы, а затем значения используемых переменных изменятся на новые. Если оптимизацию выполнить нельзя, будет запущен оригинальный байт-код цикла.Выражения и вынос кода за цикл Несмотря на то, что описываемый метод не поддерживает операции возведения в степень и «побитового И», следующий код будет оптимизирован: @cpmoptimize () def f (n, k): res = 0 for i in xrange (n): m = 3 res += ((k ** m) & 676) + i return res При анализе байт-кода декоратор сделает вывод, что значения переменных k и m в выражении (k ** m) & 676 не зависят от того, на какой итерации цикла они используются, а значит не изменяется и значение всего выражения. Вычислять его на каждой итерации не нужно, достаточно вычислить это значение один раз. Поэтому соответствующие инструкции байт-кода можно вынести и исполнять их непосредственно перед запуском цикла, подставляя в цикле уже готовое значение. Код будет будто преобразован к следующему: @cpmoptimize () def f (n, k): res = 0 _const1 = (k ** m) & 676 for i in xrange (n): m = 3 res += _const1 + i return res Такая техника известна как вынос инвариантного кода за цикл (loop-invariant code motion). Обратите внимание, что вынесенные значения вычисляются каждый раз при запуске функции, так как они могут зависеть от меняющихся глобальных переменных или параметров функции (как _const1 в примере зависит от параметра k). Получившийся код теперь легко оптимизировать с помощью матриц.Именно на этом этапе выполняется описанная выше проверка предсказуемости величин. Например, если бы один из операндов «побитового И» оказался бы непредсказуемым, эту операцию уже нельзя было бы вынести за цикл и оптимизация не могла бы быть применена.

Декоратор также частично поддерживает множественные присваивания. Если в них мало элементов, Python создаёт поддерживаемый декоратором байт-код без использования кортежей:

a, b = b, a + b Порог iters_limit На графиках выше вы могли заметить, что при малом количестве итераций оптимизированный цикл может работать медленнее обычного, так как в таком случае всё равно требуется определённое время на конструирование матриц и проверку типов. В случаях, когда необходимо, чтобы функция работала как можно быстрее и при маленьком количестве итераций, можно явно задать порог параметром iters_limit. Тогда «ловушка» перед запуском оптимизации проверит, сколько итераций предстоит выполнить циклу, и отменит оптимизацию, если это число не превышает заданный порог.Изначально порог установлен в 5000 итераций. Его нельзя установить ниже, чем в 2 итерации.

Понятно, что наиболее выгодным значением порога является точка пересечения на графике линий, соответствующих времени работы оптимизированного и исходного вариантов функции. Если установить порог именно таким, функция сможет выбирать наиболее быстрый в данном случае алгоритм (оптимизированный или исходный):

Флаг strict В некоторых случаях оптимизация должна быть обязательна применена. Так, если в цикле 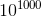итераций, без оптимизации программа попросту зависнет. На этот случай предусмотрен параметр strict. Изначально его значение равно False, но если его установить в True, то в случае, когда какой-либо из стандартных циклов for не был оптимизирован, будет возбуждено исключение.Если то, что оптимизация неприменима, было обнаружено на этапе применения декоратора, сразу будет возбуждено исключение cpmoptimize.recompiler.RecompilationError. В примере в цикле умножаются две непредсказуемые переменные:

>>> from cpmoptimize import cpmoptimize >>> >>> @cpmoptimize (strict=True) … def f (n, k): … res = 0 … for i in xrange (n): … res += i * res … return res … Traceback (most recent call last): File »», line 1, in File «cpmoptimize/__init__.py», line 100, in upgrade_func index += analyze_loop (settings, code, index) + 1 File «cpmoptimize/__init__.py», line 59, in analyze_loop raise err cpmoptimize.recompiler.RecompileError: Multiplication of two unpredictable values is unsupported Если то, что оптимизация неприменима, было обнаружено перед выполнением цикла (то есть если оказалось, что типы значений итератора или переменных не поддерживаются), будет возбуждено исключение TypeError: >>> from cpmoptimize import cpmoptimize >>> >>> @cpmoptimize (strict=True) … def f (iterable): … res = 0 … for elem in iterable: … res += elem … return res … >>> f (xrange (30)) 435 >>> f (range (30)) Traceback (most recent call last): File »», line 1, in File »», line 4, in f File «cpmoptimize/hook.py», line 170, in exec_loop raise err TypeError: Iterator in optimized loops must have type «xrange» instead of Опции дополнительной оптимизации Два флага opt_min_rows и opt_clear_stack отвечают за использование дополнительных методов оптимизации при конструировании матриц. Изначально они включены, возможность их отключения присутствует только в демонстрационных целях (благодаря ей можно сравнивать эффективность этих методов).При выполнении оптимизированного кода большую часть времени занимает перемножение длинных чисел в некоторых ячейках генерируемых матриц. Сравнительно с этим трудоёмким процессом время, расходуемое на перемножение всех остальных ячеек, пренебрежимо мало.

В процессе перекомпиляции выражений декоратор создаёт промежуточные, виртуальные переменные, отвечающие за позиции стека интерпретатора. После сложных вычислений в них могут оставаться длинные числа, которые уже сохранены в каких-то других, реальных переменных. Хранить эти значения второй раз нам уже не нужно, однако они остаются в ячейках матрицы и существенно тормозят работу программы, так как при умножении матриц мы вынуждены лишний раз перемножать эти длинные числа. Опция opt_clear_stack отвечает за очистку таких переменных: если по окончании их использования присваивать им ноль, длинные значения в них исчезнут.

Эта опция особенно эффективна, когда программа оперирует очень большими числами. Исключение лишних перемножений таких чисел позволяет ускорить программу более, чем в два раза.

Опция opt_min_rows включает минимизацию размера квадратных матриц, которые мы перемножаем. Из матриц исключаются ряды, соответствующие неиспользуемым и предсказуемым переменным. Если не используется сама переменная цикла, исключаются и ряды, отвечающие за поддержание её правильного значения. Чтобы не нарушить работу программы, после цикла всем этим переменным будут присвоены правильные конечные значения. Кроме того, в оригинальной статье вектор переменных дополнялся элементом, равным единице. Если ряд, соответствующий этому элементу, окажется неиспользуемым, он тоже будет исключён.

Эта опция может несколько ускорить программу для не очень больших n, когда числа ещё не стали очень длинными и размеры матрицы вносят ощутимый вклад во время работы программы.

Если применять обе опции одновременно, то виртуальные переменные начинают иметь предсказуемое (нулевое) значение, и opt_min_rows работает ещё эффективнее. Другими словами, эффективность обоих опций вместе больше, чем эффективность каждой из них по отдельности.

График ниже демонстрирует время работы программы для вычисления чисел Фибоначчи при отключении тех или иных опций (здесь »-m» — программа с отключённой opt_min_rows,»-c» — программа с отключённой opt_clear_stack,»-mc» — программа, где отключены обе опции сразу):

Что ещё можно реализовать? Изменение набора операций Будем говорить, что наш метод поддерживает пару операций 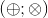, если: Мы можем выполнять операцию для двух переменных либо для переменной и константы; Мы можем выполнять операцию 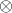для переменной и константы. Нам уже известно, что метод поддерживает пару операций . Действительно: Мы можем складывать две переменные либо переменную и константу; Мы можем умножать переменную на константу. Именно эти операции на данный момент реализованы в оптимизирующем декораторе. Однако, оказывается, что описываемый метод поддерживает и другие пары операций, в том числе (пару из умножения и операции возведения в степень).Например, наша задача может состоять в том, чтобы найти n-е число в последовательности, задаваемой рекуррентным соотношением: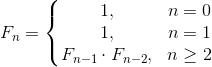

Если бы наш декоратор поддерживал пару операций , мы могли бы умножать переменную на другую переменную (но уже не могли бы складывать переменные). В таком случае следующее тривиальное решение этой задачи могло бы быть ускорено декоратором:

def f (n): a = 1 b = 1 for i in xrange (n): a, b = b, a * b return a Можно доказать, что наш метод также поддерживает пары операци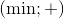й , и 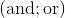 (здесь and — побитовое И, or — побитовое ИЛИ). В случае положительных чисел можно работать и с парами операци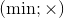й и 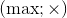.Для реализации поддержки операций можно, например, оперировать не значениями переменных, а логарифмами этих значений. Тогда умножение переменных заменится сложением логарифмов, а возведение переменной в константную степень — умножением логарифма на константу. Таким образом мы сведём задачу к уже реализованному случаю с операциями .

Объяснение того, как реализовать поддержку остальных указанных пар операций, содержит некоторое количество математичеких выкладок и достойно отдельной статьи. На данный момент лишь стоит упомянуть, что пары операции в определённой мере взаимозаменяемы.

Вложенные циклы Доработав алгоритм анализа циклов в байт-коде, можно реализовать поддержку вложенных циклов, чтобы оптимизировать код, подобный такому: def f (): res = 0 for i in xrange (10 ** 50): for j in xrange (10 ** 100): res += i * 2 + j return res Предсказуемые условия В следующем коде условие в теле цикла является предсказуемым. Можно ещё перед запуском цикла выяснить, истинно ли оно, и убрать невыполняющуюся ветку кода. Получившийся после этого код можно будет оптимизировать: def f (mode): res = 0 for i in xrange (10 ** 50): if mode == 1: res += 3 else: res += 5 return res Выводы Интерпретатор Python, вообще говоря, создаёт предсказуемый байт-код, который почти в точности соответствует тому исходному коду, который вы написали. Стандартно он не производит ни встраивания функций, ни разворачивания циклов, ни каких-либо других оптимизаций, требующих анализа поведения программы. Только с версии 2.6 CPython научился сворачивать константные арифметические выражения, но и эта возможность работает не всегда эффективно.У этой ситуации есть несколько причин. Во-первых, анализ кода в общем случае в Python затруднителен, ведь проследить за типами данных можно только во время выполнения программы (что мы и делаем в нашем случае). Во-вторых, оптимизации, как правило, всё равно не позволяют Python достичь скорости чисто компилируемых языков, поэтому в случае, когда программе нужно работать очень быстро, предлагается просто писать её на более низкоуровневом языке.

Тем не менее, Python — гибкий язык, позволяющий при необходимости реализовать многие методы оптимизации самостоятельно без вмешательства в интерпретатор. Данная библиотека, а также другие проекты, перечисленные ниже, хорошо это иллюстрируют эту возможность.

Смотрите также Ниже я приведу ссылки на несколько других интересных проектов по ускорению выполнения программ на Python: PyPy — альтернативный интерпретатор Python с поддержкой JIT-компиляции, позволяющий, как правило, выполнять программы на Python существенно быстрее. Сам PyPy написан на языке RPython, для которого специально разработан транслятор в код на языке C. Pyston — новый альтернативный интерпретатор Python, транслирующий код в промежуточное представление LLVM, из которого он может быть оптимизирован средствами LLVM и выполнен с использованием JIT-компиляции. Nuitka — компилятор Python. В отличие от упаковщика py2exe, который создаёт *.exe-файл, содержащий скрипт, интерпретатор и необходимые библиотеки, Nuitka действительно компилирует программы на Python в готовые исполняемые файлы. WPython — модифицированный интерпретатор CPython 2.6.4 с более эффективной моделью байт-кода, умной системой сворачивания констант и переработанной виртуальной машиной. astoptimizer — библиотека, применяющая известные методы оптимизации перед компиляцией в байт-код путём анализа и изменения абстрактного синтаксического дерева. promise — библиотека, оптимизирующая байт-код, полагаясь на так называемые «обещания». Если программист обещает не делать определённого рода операций в своём коде, становится возможным применить те оптимизации, которые в общем случае применить было нельзя. foldy.py — библиотека, анализирующая байт-код и выполняющая сворачивание констант (constant folding), то есть замену константных выражений на их значения, а также удаление неиспользуемых функций. Декоратор, анализирующий байт-код и выполняющий встраивание констант (constant binding), то есть заменяющий поиск значения постоянной глобальной переменной по её имени на непосредственную загрузку соответствующей константы.

© Habrahabr.ru