Автокорреляционная функция фликкер-шума19.03.2025 21:31

Введение

Под фликкер-шумом понимается шум со степенной спектральной плотностью мощности (СПМ)

$G(f) = {{1} \over {{f}^{\alpha}}}, [Вт/Гц],$

где «альфа» — безразмерный параметр, реальные значения которого лежат примерно в пределах от минус двух до двух, [1]. Разные процессы могут давать разные значения этого параметра: роль фликкер-шума простирается от электроники до социальных процессов [2]. Механизмы его формирования нетривиальны и здесь упоминаться не будут.

Прологарифмировав обе части выражения СПМ, получим линейную зависимость плотности мощности, выраженную в децибелах (дБВт), от логарифма частоты. Наклон этой прямой определяется параметром «альфа», который можно назвать крутизной СПМ. В данной работе будем рассматривать лишь положительные значения этого параметра, что соответствует моделированию низкочастотных (НЧ) шумов: медленных уходов частоты генераторов и тому подобные дрейфы физических величин.

Несмотря на то, что СПМ фликкер-шумов существует, четко определена и подтверждается множеством наблюдений [3], соответствующая авто-корреляционная функция (АКФ) может быть плохо определенной, ведь не всякий хорошо определенный сигнал имеет Фурье-образ, и наоборот. АКФ связана со СПМ парой интегральных преобразований Фурье. Наша задача состоит выявить и по возможности определить особенности АКФ для разной крутизны СПМ, что позволит адекватно оценивать и интерпретировать АКФ, полученные по результатам экспериментальных наблюдений…

Аналитически показано, что крутизна СПМ, равная единице, является точкой бифуркации: шум с

$\alpha \geq 1$

— аномальный, то есть бесконечно коррелирован в классическом понимании корреляции; шум с

$0 \leq \alpha < 1$

— нормальный в плане того, что корреляция уменьшается с увеличением лага.

Здесь и далее намеренно рассматривается именно чистая модель фликкер-шума и идеальные выражения, связывающие АКФ и СПМ. Это объясняется тем, что в теории случайных процессов хорошо изучена модель белого шума, которая, несмотря на нефизичность такого шума (его нельзя нарисовать во временной области), дает достаточно точные результаты, если СПМ физического шума является равномерной в рабочей полосе частот некоторого радиотехнического звена.

В достаточно фундаментальной работе [3] сделана оценка АКФ фликкер-шума с единичным параметром «альфа» — то есть для розового шума, — снимаемого с измерительного устройства с П-образной АЧХ, в результате чего из-за прерывания высоких частот на графике АКФ наблюдаются некоторые осцилляции. Несмотря на отсутствие выражений АКФ для других значений параметра «альфа», в этой работе имеется много экспериментальных результатов: таблиц, графиков, а также даны детальные объяснения физики процессов, хоть и местами труднопонимаемые для инженерного восприятия.

Целью данной работы является получение — часто с помощью систем компьютерной алгебры (СКА) — максимально точных и доступных оценок АКФ фликкер-шума, не обращая внимания на природу такого шума и разного рода технические эксперименты.

Основная часть

Запишем выражение для авто-корреляционной функции (АКФ)

$R(\tau) = 2 \int_{0}^{\infty}{ G(f) \cos(2 \pi f \tau) df}.$

Здесь, естественно, учтено, что СПМ по определению должна быть четной функцией (и не отрицательной). В этом плане в первоначальном выражении СПМ надо поставить знак модуля от частоты, который для упрощения опущен. Также будем везде считать, что лаг неотрицательный.

Подставим СПМ фликкер-шума в выражение для АКФ, и сделаем замену переменной

$fx = \tau,$ $R(\tau) = 2 {\tau}^{\alpha-1} \int_{0}^{\infty}{ {{1} \over {x^{\alpha}}} \cos(2 \pi x) dx}.$

Удивительно, но зависимость от лага формально найдена в явном виде для любого параметра «альфа» — зависимость степенная. Интеграл здесь — это лишь некоторая функция параметра, не зависящая от лага. Используя справочник интегралов [4], можно записать точный результат в более удобном для практических расчетов виде

$R(\tau) = {{2} \over {(2 \pi \tau)}^{1-\alpha}} \Gamma(1 - \alpha) \cos(\pi(1-\alpha)/2), ~~~~~0 < \alpha < 1, ~~\tau>0.» src=«https://habrastorage.org/getpro/habr/upload_files/4b6/ef0/b86/4b6ef0b86e265777be6ce008b6deb72c.svg» /><p>Правда, здесь результат только для ограниченного параметра шума: когда шум не является аномальным. В этом случае АКФ убывает с ростом лага, пусть даже и медленно для параметра «альфа» близкого к единице слева</p><img alt=$

Этот результат можно получить, используя известное тождество для гамма-функции

$z \Gamma(z) = \Gamma(z+1)$

для малого аргумента. В пределе при «альфа» стремящемся к единице, АКФ хоть и бесконечна, но не зависит от лага, то есть является константой.

Если параметр «альфа» близок к нулю, то АКФ имеет следующую асимптотику

$R(\tau) \approx {{{\alpha} \over {2}} {{1} \over {\tau}}}, ~~~\alpha \approx 0.$

Недостатком полученных формул для АКФ, помимо ограниченного интервала

$0 < \alpha < 1$

является то, что они расходятся при нулевом лаге, что не позволяет получить форму нормированной АКФ, которую оценивают практически. Поэтому найдем асимптотики выражений АКФ, позволяющие корректно нормировать АКФ и находить предельные формы АКФ, к которым должны стремиться практические оценки.

НЧ фликкер-шум с доминированием высоких частот

Рассмотрим интервал

$0 \leq \alpha < 1.$

В этом случае АКФ плохо определена для малых лагов, то есть в области высоких частот СПМ, потому что интеграл Фурье расходится при неограниченном увеличении частоты. Введем верхнюю частоту в спектре сигнала

$F_в = {{1} \over {2\Delta t}},$

где

$\Delta t$

— интервал взятия отсчетов, определяющий интервал поступления новых измерений шума, или частоту дискретизации, равную удвоенной верхней частоте. Верхняя означает максимально наблюдаемая, в то время как физически измеряемый шум может иметь более узкую полосу — это уже детали конкретного эксперимента.

Используя СКА SymPy Live Shell, найдем выражение для исходной АКФ

$R(0) = {{2 {{F}_{в}}^{1 - \alpha}} \over {1 - \alpha}},$ $r(\tau) = R(\tau) / R(0) = {_1}{F_2} \left({{1 \over 2}} - {{\alpha} \over {2}}; {1 \over 2}, {3 \over 2} - {{\alpha} \over {2}}; -\pi^2 {F_в}^{2} {\tau}^{2} \right).$

Здесь

— оценка дисперсии шума при конечной верхней частоте,

$r(\tau)$

— нормированная к среднему квадрату форма АКФ,

${_1}{F_2(a;b,c;x)}$

— гипергеометрическая функция. Последняя, к сожалению, не так распространена в справочниках и библиотеках численного расчета, как ее зеркальный собрат

Однако, в случае

$\alpha = 1/2$

можно найти более практичное выражение

$r(\tau) = {{1} \over {2}} {{-i} \over {\sqrt{F_в \tau}}} C\left( 2i \sqrt{{F_в} \tau} \right),$

где

— косинусный интеграл Френеля. В остальных случаях можно использовать специальные библиотеки для численного расчета [5], либо более продвинутые СКА.

Представляя лаг в дискретном виде, безразмерный параметр

$2{F}_{в} \tau$

будет представлять собой номер отсчета АКФ, начиная с нуля, так что

Код для построения АКФ с параметром альфа равным 0,5

from matplotlib import pyplot as plt
from scipy.special import fresnel
import numpy as np

def akf_flikker_alpha_0_5(t, F1):
    def inner_func(x): # Скалярная функция.
        x = 2 * 1j * np.sqrt(x)
        _, C = fresnel(x)
        return np.real(C / x) if x != 0 else 1
    inner_func_fn = np.vectorize(inner_func, otypes=(float,))
    return inner_func_fn(t * F1)

def F8(n: int):
    F1 = 1.
    Td = 1/(2*F1)
    part_of_lag = 0.01 # Процент по лагу, чтобы видеть область малых лагов.
    x = np.linspace(0, part_of_lag * n*Td, num=n)
    alpha = 0.5
    #y1 = akf_flikker_noise(x, F1, alpha)
    y2 = akf_flikker_alpha_0_5(x, F1)
    plt.plot(x, y2)
    plt.xlabel(r'Лаг')
    plt.ylabel(r'$r(\tau)$')
    plt.legend([f'Theory: $\\alpha = {alpha}$'])
    plt.title(f'{100*part_of_lag}% АКФ фликкер шума при верхней частоте $F_в$ = {F1}')
    plt.grid(True)
    plt.show()

if __name__ == "__main__":
    F8(1024)

На бесконечности интеграл Френеля стремится к константе, поэтому АКФ убывает как корень квадратный лага. Уровню корреляции 0,5 соответствует параметр

${F}_{в} \tau \approx 0,417.$

В области малых лагов АКФ убывает по квадратичному закону, см. рисунок ниже.

АКФ фликкер-шума с параметром, ограниченного по полосе верхней частотой. Интервал взятия отсчетов шума равен. Корреляция в точках, кратных этому интервалу, ненулевая - отсчеты такого шума коррелированы

АКФ фликкер-шума с параметром $\alpha = 0,5$ , ограниченного по полосе верхней частотой

. Интервал взятия отсчетов шума равен 0,5

. Корреляция в точках, кратных этому интервалу, ненулевая — отсчеты такого шума коррелированы

Удалось найти выражения при $\alpha = 0$

$r(\tau) = {{\pi} \over {2}} {I}_{0,5}\left(i \pi {F}_{в} \tau \right){I}_{-0,5} \left(i \pi {F}_{в} \tau \right).$

Здесь

${I}_{\pm 0,5}(.)$

— модифицированные функции Бесселя. В пределе, для большого аргумента выражение АКФ должно давать символ Кронекера — цифровую дельта-функцию. На бесконечности данная АКФ убывает обратно пропорционально лагу. В области малых лагов АКФ убывает по квадратичному закону. Уровню корреляции 0,5 соответствует параметр

${F}_{в} \tau \approx 0,3015.$

АКФ белого шума ограниченного по полосе верхней частотой

. Интервал взятия отсчетов шума равен 0,5

. Корреляция в точках, кратных этому интервалу, нулевая — отсчеты белого шума некоррелированы

Дополнительные функции для вычисления АКФ

from scipy.special import iv
from mpmath import hyp1f2

def akf_flikker_alpha_0(t, F1): # Должна совпадать с akf_flikker_noise(.) при alpha = 0.    
	def inner_func(x): # Скалярная функция.        
		x = np.pi * 1j * x
  		return 0.5 * np.pi * np.real(iv(0.5, x) * iv(-0.5, x)) if x != 0 else 1
    inner_func_fn = np.vectorize(inner_func, otypes=(float,))
    return inner_func_fn(t * F1)

def akf_flikker_noise(t, F1, alpha):    
	assert(alpha < 1)    
  	assert(alpha >= 0)    
  	hyp1f2_fn = np.vectorize(hyp1f2, otypes=(float,))    
  	return hyp1f2_fn(0.5 - 0.5*alpha, 0.5, 1.5 - 0.5*alpha, -np.pi**2 * (F1 * t)**2)

НЧ фликкер-шум с доминированием низких частот

Осталось понять, что происходит при

$\alpha \geq 1.$

Здесь исходный интеграл Фурье расходится для низких частот. Минимальная (т.е. нижняя) частота при практических наблюдениях определяется длительностью наблюдаемой реализации T

$F_н = {{1} \over {2T}}.$

Здесь взят удвоенный интервал наблюдения, потому что полная АКФ по определению рассчитывается на двойной интервал. Рассматривая интеграл от данной нижней частоты до бесконечности, получим следующие выражения АКФ

$R(0) = {{(\alpha - 1) {{F}_{н}}^{\alpha-1}} \over {2}},$ $r(\tau) = {\sqrt{\pi} (\alpha-1) \over {2}} {\left({{\pi^{\alpha-1} {(F_н \tau)}^{\alpha-1} \Gamma({{1-\alpha} \over {2}})} \over {\Gamma(\alpha/2)}} + {{ \Gamma({{\alpha-1} \over {2}})} \over {\sqrt{\pi} \Gamma({{\alpha+1}\over{2}})}} {_1F_2(.)} \right)}.$

Здесь гипергеометрическая функция имеет вид

${_1F_2 \left({{1 - \alpha} \over {2}};{{1}\over{2}},{{3-\alpha}\over{2}};-\pi^2 {{F}{н}}^{2}{\tau}^{2} \right) }.$

При таком раскладе удалось найти выражение АКФ для пограничного случая

$\alpha = 1$

— розовый шум

$r(\tau) = {{1 + \cos(2 \pi {F}_{н} \tau)} \over {2}}.$

Данная форма является искусственной в том плане, что эта АКФ при устремлении нижней частоты к нулю становится равной константе — розовый шум имеет аномальную природу. То есть идеальный розовый шум имеет бесконечную корреляцию. Косинусная форма является артефактом практических наблюдений. Правда, заметим, что если нижняя частота имеет физически объяснимую природу (не инструментальную), то есть когда измеряются заведомо длинные реализации, перекрывающие физически существующие низкие частоты, то тогда эта форма будет определять реальную АКФ розового шумового процесса.

Удалось найти выражение АКФ для броуновского (коричневого) шума,

$\alpha = 2,$ $r(\tau) = - {\pi}^{2} {F}_{н} \tau + 2 \pi {F}_{н} \tau \cdot Si(2 \pi {F}_{н} \tau) + \cos(2 \pi {F}_{н} \tau),$

где

— интегральный синус.

Код для построения экспериментальной и теоретической АКФ броуновского шума, ограниченного нижней частотой F0

from matplotlib import pyplot as plt
from scipy.special import gamma
from scipy.special import sici
from scipy.special import fresnel
from scipy.special import iv
from scipy import signal
from scipy import fft
import numpy as np
from numba import jit
from mpmath import hyp1f2

@jit(nopython=True)
def leaky_integrator_jitted(x, state = 0., leakiness = 1.):
    y = np.zeros(len(x), dtype=np.float64)
    for i in range(len(x)):
        if i == 0:
            y[i] = x[i] + state * leakiness
        else:
            y[i] = x[i] + y[i-1] * leakiness
    return y

def brown_noise(n: int):
    return leaky_integrator_jitted(np.random.normal(0, 1, n))

def akf_brown_noise(t, F0):
    x = 2 * np.pi * t * F0
    pi_sqrt = np.sqrt( np.pi )
    Si, _ = sici(x)
    return pi_sqrt/2 * (-pi_sqrt * x + (2/pi_sqrt) * (x*Si + np.cos(x)))

def AKF(n: int, m: int):
    akf = np.zeros((2*n-1,), dtype=np.float64)
    for _ in range(m):
        noise = brown_noise(n)
        noise -= np.mean(noise)
        akf += signal.correlate(noise, noise, method='fft')
    idx = np.argmax(akf)
    assert(np.isscalar(idx))
    akf /= akf[idx]
    lags = signal.correlation_lags(n, n)
    return akf, lags

def F5(n: int, m: int):
    akf_brown, lags = AKF(n, m)
    x = np.linspace(0, n, num=n)
    akf_theory = akf_brown_noise(x, 0.5/n)
    plt.plot(lags[n-1:], akf_brown[n-1:], x, akf_theory)
    plt.legend(['Эксперимент', 'Теория'])
    plt.xlabel(r'Лаг')
    plt.ylabel(r'$r(\tau)$')
    plt.title(f'АКФ модельного броуновского шума')
    plt.grid(True)
    plt.show()

if __name__ == "__main__":
    F5(1024, 256)

Опять-таки, при устремлении нижней частоты к нулю АКФ становится равной константе — броуновский шум имеет аномальную природу. Наблюдаемый спад экспериментальных АКФ — это, фактически, результат конечной выборки, см. рисунок ниже.

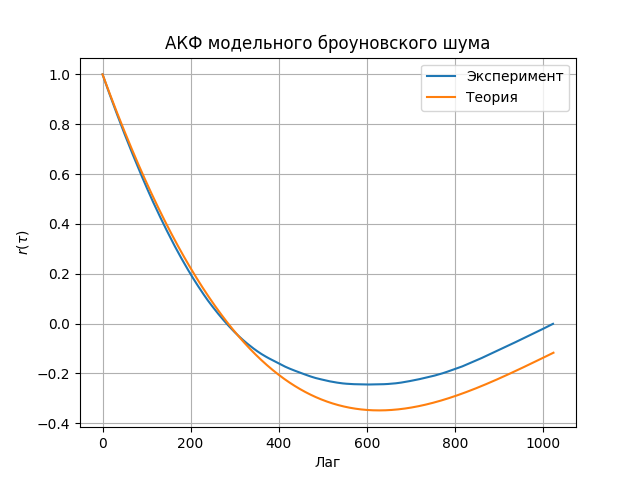
АКФ броуновского шума, полученного интегрированием дискретного белого гауссовского шума. Оценка АКФ сделана через конструкцию signal.correlate (noise, noise, method='fft') библиотеки SciPy. Перед оценкой АКФ из модельной реализации вычиталось её среднее значение

Расхождение для больших лагов, вероятно, вызвано вычитанием постоянной составляющей из реализаций шума. Однако, для корректных оценок АКФ вблизи малых лагов такое вычитание необходимо, потому что вывод теоретической формулы предполагает интегрирование от малой, но ненулевой частоты. Теоретическое выражение предполагает идеальную фильтрацию в непрерывной области частот, практическая же оценка предполагает также идеальную фильтрацию, но в дискретной частотной области. Если частоты дискретные, то АКФ периодическая, значит при практических оценках происходит наложение АКФ друг на друга. Вероятно, по этой причине при практических оценках доверяют примерно четверти диапазона лагов.

Заметим, что классический интегратор, фильтрующий белый гауссовский шум

Код использованный для генерации и построения броуновского шума

from matplotlib import pyplot as plt
import numpy as np
from numba import jit

@jit(nopython=True)
def leaky_integrator_jitted(x, state = 0., leakiness = 1.):
    y = np.zeros(len(x), dtype=np.float64)
    for i in range(len(x)):
        if i == 0:
            y[i] = x[i] + state * leakiness
        else:
            y[i] = x[i] + y[i-1] * leakiness
    return y

def brown_noise(n: int):
    return leaky_integrator_jitted(np.random.normal(0, 1, n))

def F3(n: int, m: int):
    z = [brown_noise(n) for _ in range(m)]
    labels = [r'' for _ in range(m)]
    x = range(n)
    for y, l in zip(z, labels):
        plt.plot(x, y)
    plt.xlabel(r'Sample')
    plt.ylabel(r'Noise')
    plt.title(f'Броуновские шумы, формируемые дискретным \n'
                'интегратором из белого нормального шума')
    plt.grid(True)
    plt.show()

if __name__ == "__main__":
    F3(32768, 16)

дает фликкер-шум с параметром СПМ

$\alpha = 2,$

что говорит о довольно-таки сильном «денормализующем» влиянии интегратора — возникает дрейф с неконтролируемой (расходящейся) дисперсией, что говорит от нестационарности броуновского шума, хотя средний спектр (т.е. СПМ) такого шума хорошо определен.

Набор из

реализация броуновских шумов, 32768

отсчетов. Разворачивание процессов идет из нулевого начального состояния

Поэтому имеются способы находить дробные производные и интегралы (в дискретном виде), например, чтобы иметь больше степеней свободы при проектировании ПИД-регуляторов [6].

В качестве справки приведем выражение АКФ для

$\alpha = 3/2,$ $r(\tau) = \pi \sqrt{F_н \tau} \left(2 S(2 \sqrt{F_н \tau}) - 1 \right) + \cos(2 \pi F_н \tau), ~\tau \geq 0,$

которое было найдено с помощью более мощной СКА Wolfram Alpha по онлайн запросу

simplify HypergeometricPFQ[{-1/4},{3/4,1/2}, -pi^2 * z^2] - pi*sqrt(z)

Здесь

— синусный интеграл Френеля. Данная АКФ вблизи малых лагов убывает по закону корня квадратного от лага.

Заметим, что в найденных выражениях АКФ везде встречается гипергеометрическая функция

${}_1{F}_{2}(...),$

что независимо подтверждается работой [7].

Заключение

С помощью систем компьютерной алгебры получено аналитическое выражение для авто-корреляционной функции фликкер-шума, спектральная плотность мощности которого имеет параметр

$0 \leq \alpha < 1.$

Такой шум назван «нормальным» в том плане, что корреляция убывает с ростом лага. Зависимость от лага — степенная.

Для аномального фликкер-шума — шума с параметром

$\alpha \geq 1$

найдены асимптотики АКФ относительно минимальной нижней частоты в спектре. Зависимости от лага нет, а зависимость от нижней частоты — степенная, исчезающая при устремлении нижней частоты к нулю. Сделано сравнение АКФ, оцененной для модельного броуновского шума и АКФ, найденной теоретически: они хорошо совпадают для малых лагов, которые меньше четверти длительности экспериментальной реализации.

Вдохновением для данной статьи стало обсуждение особенностей фликкер-шума в комментариях к публикации с хабра-юзером @adeshere, которому выражается отдельная благодарность.

Список источников

Модели спектральной плотности мощности фликкер-шумов, Борисов Б.Д., АИПИ-2–2015–8, Автоматика и программная инженерия, 2015, No 2(12), доступ 16.03.2025
Фликкер-шум, доступ 11.03.2025.
Низкочастотный токовый шум со спектром типа1/f в твердых телах, М. Коган, УФН, Т.145, вып. 2, 1985.
Таблицы интегралов, сумм, рядов и произведений. И.С. Градштейн, И.М. Рыжик, изд 4-е, 1963, параграф 3.761, формула 9, стр. 435.
Библиотека Hypergeometric functions — mpmath 1.3.0 documentation.
Some Applications of Fractional Calculus in Engineering, Mathematical Problems in Engineering, Volume 2010, Article ID 639801, 34 pages, doi:10.1155/2010/639801.
Some Identities with Generalized Hypergeometric Functions, Vasily E. Tarasov, Appl. Math. Inf. Sci. 10, No. 5, 1729–1734 (2016).