Ардуино головного мозга: импульсный датчик положения
Задача на сегодня: как определить угол поворота инкрементального энкодера?
Сегодня в серии публикаций про ардуино головного мозга коротенькая статья с небольшим экспериментом и парой рецептов. В комментариях к одной из моих прошлых статей меня обвинили в том, что ардуиной подсчитывать импульсы энкодера — фу так делать:
Оптически энкодер 1000/оборот и ATMega не имеющая аппаратной схемы работы с энкодером (как у серий STM32, например) — это тупик.
Дальше в комментариях было много теоретизирования, которое лучше пропустить. Давайте лучше попробуем протестировать в железе, насколько это тупик. Для начала, что такое инкрементальный энкодер? Тот, кто помнит эпоху до-оптических мышек, ответ знает точно.
Внутри энкодера есть диск с прорезями, вот для наглядности я сделал фотографию диска с пятьюстами прорезями:

С одной стороны этого диска помещают светодиод, с другой фотодиод:

Вращаясь, диск то пропускает свет на фотодиод (если прорезь напротив пары светодиод-фотодиод), то не пропускает. При постоянной скорости вращения на выходе фотодиода получается красивая синусоида (не забываем, что поток света может быть перекрыт частично). Если этот сигнал пропустить через компаратор, то получится сигнал прямоугольной формы. Подсчитывая количество импульсов сигнала, получим насколько провернулся вал датчика.
Как же определяется направление вращения? Очень просто: в датчике не одна, а две пары светодиод-фотодиод. Давайте нарисуем наш диск, точки A и B показывают положение фотодатчиков. При вращении вала энкодера снимаем два сигнала с этих фотодатчиков:
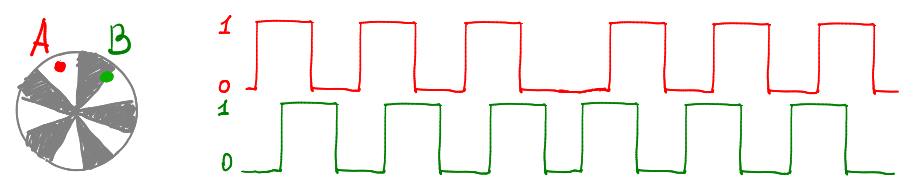
Датчики поставлены на таком расстоянии, чтобы при вращении с постоянной скоростью генерировался меандр, свинутый на четверть периода. Это означает, что когда фотодатчик А стоит напротив середины прорези, то фотодатчик B стоит ровно на границе прорези. Когда датчик крутится (условно) по часовой стрелке, то при восходящем фронте на сигнале B сигнал A равен единице. Когда же датчик крутится в обратную сторону, то при восходящем фронте на сигнале B, а равен нулю.
Это всё прекрасно, но что мне копипейстить в мой проект?
Вот это:
volatile long angle = 0;
volatile char ABprev = 0;
const int increment[16] = {0,-1,1,0, 1,0,0,-1, -1,0,0,1, 0,1,-1,0};
ISR (PCINT0_vect) { // D8 or D9 has changed
char AB = PINB & 3;
angle += increment[AB+ABprev*4];
ABprev = AB;
}
void setup() {
pinMode(8, INPUT); // A
pinMode(9, INPUT); // B
PCICR |= (1 << PCIE0); // interrupt will be fired on any change on pins d8 and d9
PCMSK0 |= 3;
ABprev = PINB & 3;
Serial.begin(115200);
}
void loop() {
Serial.println(angle);
delay(100);
}
Давайте объясню, как этот код работает. Я тестирую код на ATmega328p (Arduino nano), выходы энкодера поставлены на пины d8 и d9 arduino nano. В терминах ATmega328p это означает, что младшие два бита порта PINB дают текущее состояние энкодера. Функция ISR будет вызвана при любом изменении в этих двух битах. Внутри прерывания я сохраняю состояние энкодера в переменную AB:
char AB = PINB & 3; // Внимание, ардуиновский digitalRead() противопоказан,
// когда нам критична скорость работы
Для чего? Давайте посмотрим на предыдущий график, в нём пунктирными линиями обозначены моменты вызова прерывания (любой фронт на любом сигнале). Для каждого вызова прерывания цифры внизу — это состояние переменной AB:
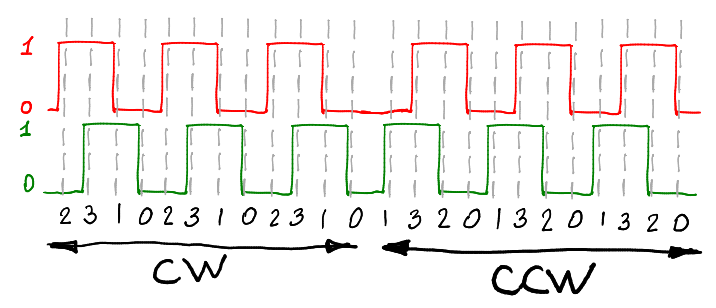
Видно, что при вращении по часовой стрелке переменная AB меняется с периодом в четыре значения: 231023102310. При вращении против часовой стрели переменная AB меняется 013201320132.
Если у нас оба фотодатчика были перекрыты (переменная AB=0), а при вызове прерывания AB становится равной 2, то датчик вращается по часовой стрелке, добавим к счётчику единицу. Если же AB переходит от 0 к 1, то датчик вращается против часовой стрелки, отнимем единицу от счётчика. То же самое и с другими изменениями переменной AB, давайте составим таблицу:
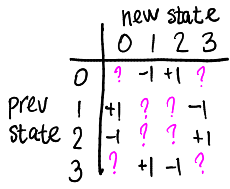
Обратите внимание, что таблица заполнена не до конца. Что вставить на месте вопросительных знаков? Например, по идее, главная диагональ таблицы не должна использоваться никогда, прерывание вызывается при изменении переменной AB, поэтому перехода 0→0 случаться не должно. Но жизнь штука тяжёлая, и если микроконтроллер занят, то он может пропустить несколько прерываний и таки вызваться. В таком случае предлагаю ничего не прибавлять и не отнимать, так как нам явно не хватает данных; заполним недостающие клетки нулями, вот наша таблица:
const int increment[16] = {0,-1,1,0, 1,0,0,-1, -1,0,0,1, 0,1,-1,0};
Теперь, надеюсь, код понятен полностью.
В итоге на один период сигнала A у нас вызывается четыре прерывания, что при вращении датчика в одну сторону увеличит счётчик не на 1, но на 4. То есть, если на инкрементальном энкодере написано 2000PPR (две тысячи прорезей на диске), то реальное его разрешение составляет 1/8000 оборота.
Постойте, а что с дребезгом?
Пропуская синусоиду через компаратор, мы неизбежно получим дребезг на фронтах нашего сигнала прямоугольной формы. Давайте возьмём лупу и посмотрим на один фронтов:
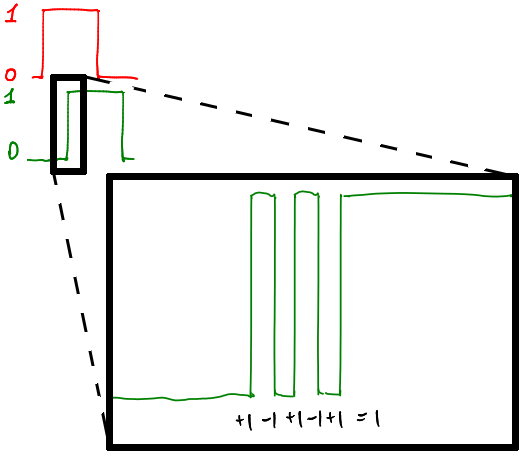
Сигнал A постоянный, поэтому согласно нашей табличке, на восходящем фронте сигнала B мы добавляем единицу, а на нисходящем вычитаем. В итоге, если мы сумеем отработать все фронты нашего дребезга, то наш алгоритм его прекрасно проглотит. И вот тут становится интересно, а сможет ли наша ардуинка отработать такие прелести? Теоретизировать можно долго, давайте ставить эксперимент.
От теории к практике
Считать импульсы будем тремя способами:
- Софтверно на ATmega328p
- ATmega328p, опрашивающая хардверный счётчик
- BeagleBone Blue
Все три способа считают импульсы абсолютно одинаково, но, разумеется, хардверные способы имеют существенно большую скорость опроса сигналов. Энкодер используется Omron E6B2-CWZ6C (2000PPR).
Подключение
Софтверный счётчик
Подключение простейшее, достаточно два провода от энкодера завести на ноги d8 и d9 ардуины.
HCTL-2032
Подключение hctl-2032 к ардуине выглядит примерно вот так:

Чтобы не занимать все ноги ардуины, я поставил ещё 74hc165.
BeagleBone Blue

BeagleBone Blue имеет встроенный квадратурный декодер, поэтому 3.3В энкодеры можно просто завести на соответствующий коннектор. У меня энкодер имеет 5В логику, поэтому я добавил двусторонний преобразователь уровней на bss138:

Эксперимент первый
Я взял свой стенд с маятником, который уже описывал:

Каретка ездить не будет, просто повешу три счётчика на энкодер маятника. Почему именно маятник? Потому что сила тяжести даёт неуплывающий маркер: каждый раз, как маятник успокаивается в нижем положении, счётчики должны показывать число, кратное 8000 (у меня энкодер 2000ppr).
Вот три счётчика, подключенные параллельно, сверху вниз: биглбон, софтверный счётчик, hctl2032. ШИМ-драйвер для двигателя каретки в данном тесте не используется:

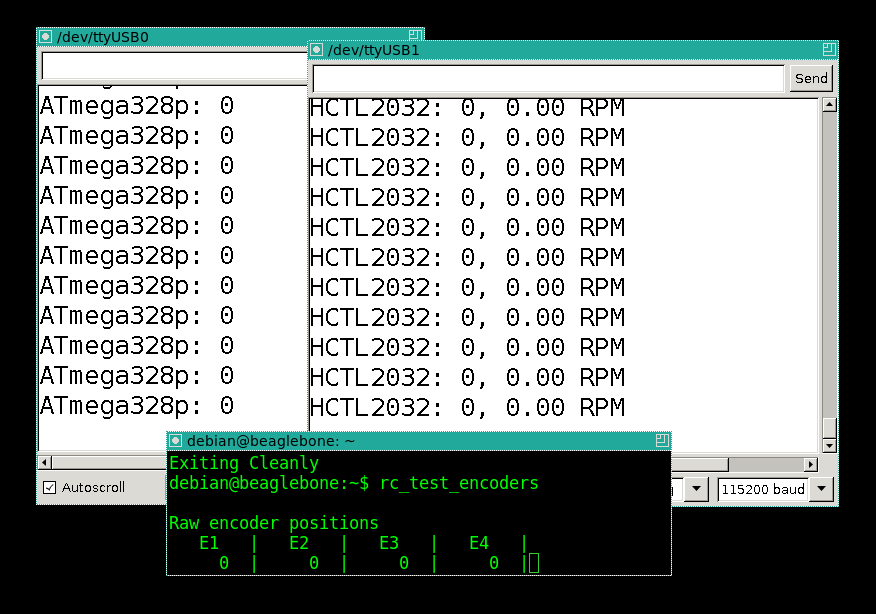
Начало испытаний, маятник неподвижен, два монитора последовательных портов и счётчик биглбона, запущенный по ssh:
Рукой делаю один полный поворот маятника, жду, пока он снова успокоится в нижнем положении:
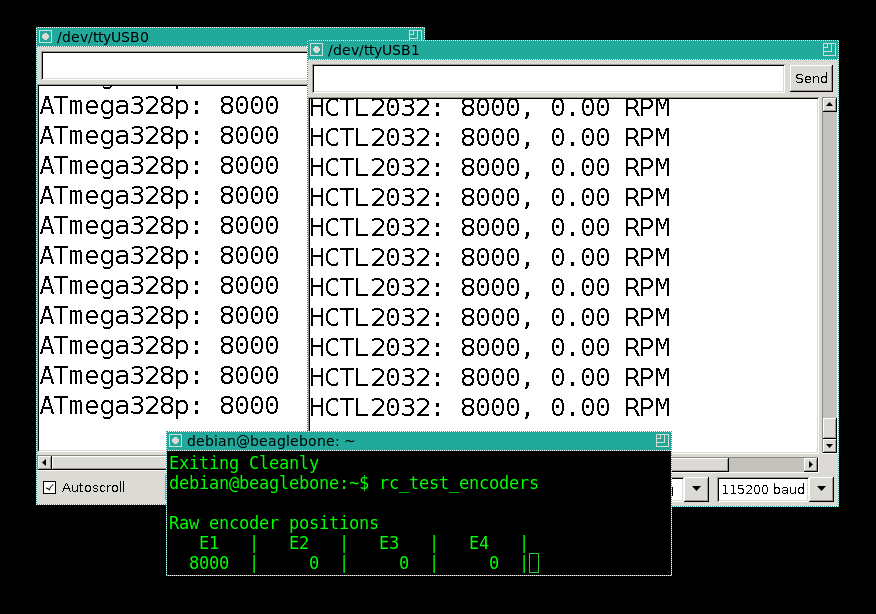
Все три счётчика показывают ровно 8000, как и положено! Хорошо, из комментариев мы вынесли, что из-за дребезга софтверный счётчик должен сильно ошибаться при низких скоростях маятника. Десять раз повторяю процедуру: качаю маятник так, чтобы он сделал один оборот, а затем жду, пока полностью успокоится. Затем снова качаю, жду, покуда успокоится. Трение низкое, одна итерация занимает пару минут, в итоге примерно полчаса работы счётчиков.
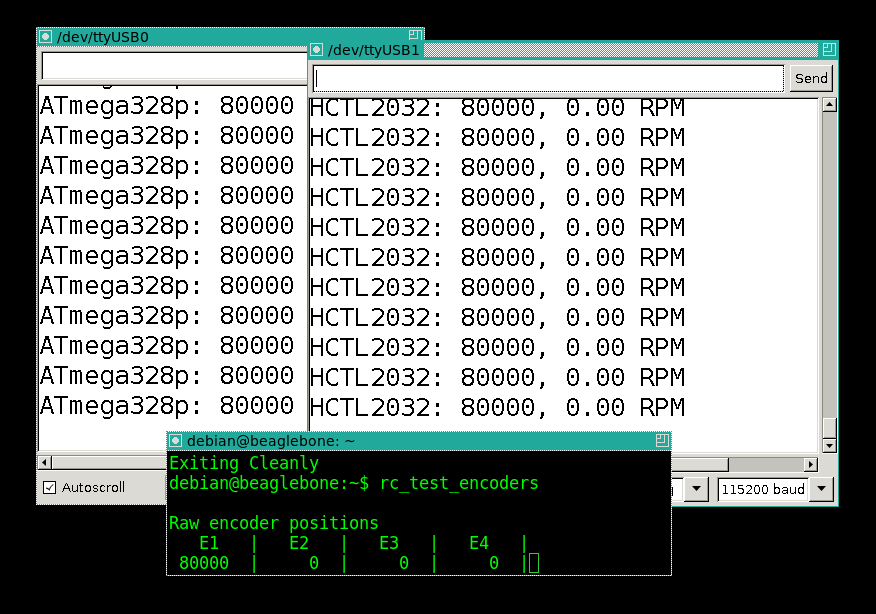
Ха, а ведь опять ни один не ошибся!
Эксперимент второй
Итак, дребезг в реальности оказался не столь страшным, как казалось. Снимаю маятник, и цепляю к оси энкодера шуруповёрт:

Дальше потихоньку увеличиваю обороты, периодически останавливаясь, и проверяя, насколько все три счётчика согласны с происходящим. Именно поэтому у меня в одном из окон есть оценка скорости вращения вала энкодера.
100 оборотов в минуту — порядок. 500 оборотов в минуту — порядок, согласие полное. 900 оборотов в минуту: АГА! Останавливаю шуруповёрт:
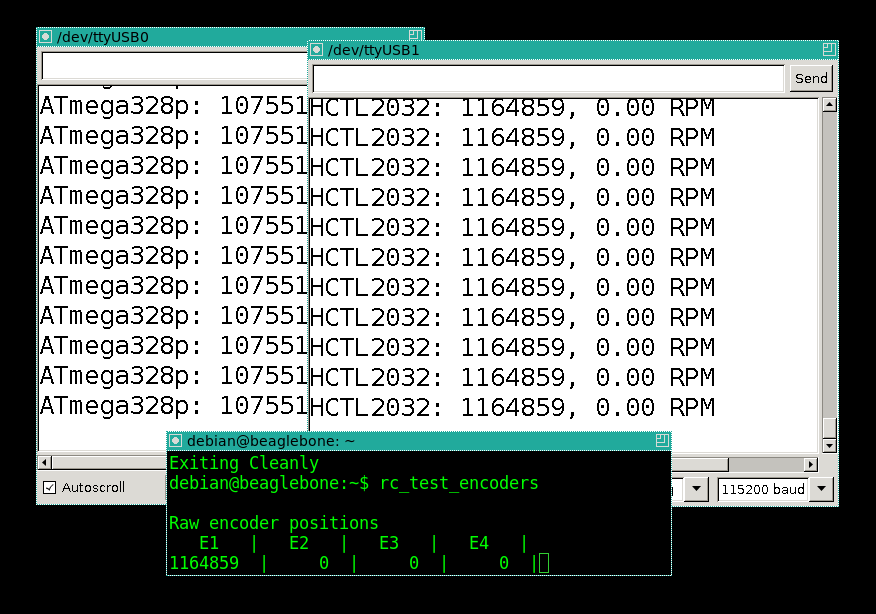
Хардверные счётчики по-прежнему согласны между собой, а вот софтверный прилично отстал. Давайте считать, насколько это согласуется с теорией. Мануал на ATmega328p говорит, что обработка (пустого) прерывания — это минимум 10 тактов микроконтроллера. Работа со стеком, чуть кода внутри прерывания — это в сумме тактов 40 на одно прерывание. 8000 тысяч прерываний на 900 оборотов в минуту (15 оборотов в секунду) на 40 тактов = 4800000 тактов в секунду. В целом наша оценка весьма недалека от тактовой частоты ардуины, то есть, 1000 оборотов в минуту — это потолок для счётчика энкодера высокого разрешения на прерываниях, причём для ардуины, которая не делает ничего другого.
На 2000 оборотов в минуту оба хардверных счётчика работали без рассогласований, а больше у меня шуруповёрт выдать не может.
Подведём итог:
1. Считать на прерываниях вполне можно, 15 оборотов в секунду — это всё же весьма приличная скорость. Но если нужно обрабатывать больше одного счётчика, всё становится резко хуже.
2. Хардверные счётчики надёжнее, но дороже.
3. hctl2032 существенно дешевле BeagleBone Blue, но и сложнее подключается к контроллеру, а биглбон и сам себе контроллер, и умеет четыре энкодера разом обрабатывать. Да и усилитель для двигателя там уже есть на борту, поэтому стенд с маятником можно собрать вообще малой кровью.
4. Говорят, stm32 и дёшев, и имеет хардверный счётчик. Но цена вхождения (в смысле времени) в вопрос больно кусается.
