Аппроксимация числа Пи с помощью множества Мандельброта
Я всегда говорил своему другу, что математика со своими изящными абстракциями обладают той магической силой, потенциал которой до сих пор полностью не раскрыт. Сегодня я хочу поговорить о том, как можно приблизить число Пи с помощью множества Мандельброта.
Пару слов о множестве
На самом деле на Хабре куча статей, описывающие множество Мандельброта (далее, множество М), рассматривающие его свойства, историю и удивительную красоту, подкрепляя всё это красочными картинками. Мне бы не хотелось останавливаться на его определении и прочих деталях, а сразу перейти к делу. Однако в силу того, что оно является центральным субъектом данной статьи, я все же освежу вашу память.
Множество М — это множество всех комплексных чисел с, для которых функция 

На практике мы применяем следующую теорему: если функция (вышеприведенная) в ходе итерации превосходит значение 2, то она 100% не ограничена. Поэтому, определить множество можно так:


Я не буду затрагивать тему визуализации, туда мы сегодня копать не будем.
Число Пи?
Действительно, каким-таким образом?
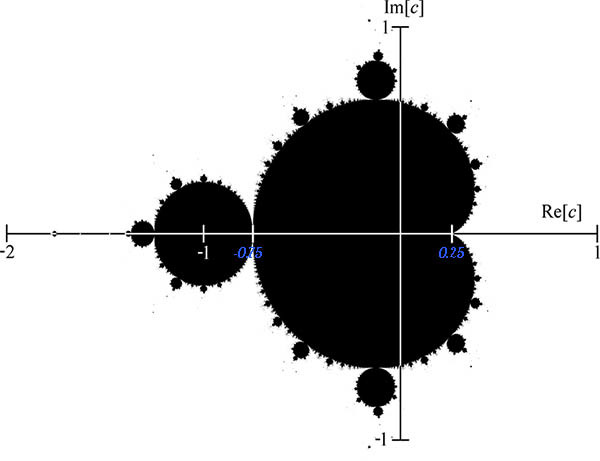
Возьмем «координату соприкосновения двух частей» множества c = -0.75 + ix (где x ∈ ℚ). Проверим её принадлежность ко множеству М: начнем итерировать функцию 
| x | c | n (кол-во итераций до расхода функции) |
|---|---|---|
| 0.1 | -0.75 + 0.1i | 33 |
| 0.01 | -0.75 + 0.01i | 315 |
| 0.001 | -0.75 + 0.001i | 3143 |
| 0.0001 | -0.75 + 0.0001i | 31417 |
| 0.00001 | -0.75 + 0.00001i | 314160 |
Именно. Если поставить запятую на нужном месте, цифры напоминают число Пи.
Наверное, совпадение
Не будем заморачиваться с комплексной частью и возьмем число c = 0.25. Оно принадлежит множеству при бесконечно большом количестве итераций. Поэтому, будем «приближаться» к этой точке справа: возьмем c = 0.26, проверим его; c = 0.2501, проверим его, и т. д.
| c | n (кол-во итераций до расхода функции) |
|---|---|
| 0.26 | 30 |
| 0.2501 | 312 |
| 0.25001 | 991 |
| 0.250001 | 3140 |
| 0.2500001 | 9933 |
| 0.25000001 | 31414 |
Последовательность колеблется между двумя значениями, однако эхо числа Пи (поставив запятую в нужное место) никуда не исчезло.
Немного истории
Само множество М, названное в честь математика Бенуа Мандельброта — совсем недавное открытие. Бенуа даже выступал на TEDx, говоря в том числе и о нем.
В 1991 Дейв Болл изучал, действительно ли «соприкосновение двух частей множества» М около c = -0.75 «бесконечно тонко». В ходе своего исследования он и обнаружил то, о чем мы сейчас говорим.
И все-таки, наверное, совпадение
Попытаемся понять, что происходит: действительно ли мы получаем число Пи или это какое-то иное трансцендентное число.
Все это будем делать вокруг точки c = 0.25 (просто в силу отсутствия у него комплексной части — так легче).
Рассмотрим рекурсивную функцию 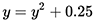 . При ее итерации от нуля заметим, что она очень медленно стремится к точке x = 0.5.
. При ее итерации от нуля заметим, что она очень медленно стремится к точке x = 0.5.

Чтобы не дать ей «застрять» на этом значении, мы подвинем данную функцию на ε единиц вверх (ε бесконечно мало, не равно нулю). Тогда она примет вид 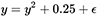 .
.
Данная функция медленно стремится к точке x = 0.5, а после того, как проходит её, быстро убегает в бесконечность.
Будем копать дальше.
Пусть x = y + 0.5. Наша задача — найти ноль.
Делая замену в исходной функции, получим: 
Взяв в качестве ε любое малое значение, проитерируем функцию от нуля:
| y |
|---|
| 0.001 (= ε) |
| 0.002001 |
| 0.0030050040010000004 |
| 0.004014034050046026 |
| 0.005030146519400955 |
| 0.006055448893407596 |
| 0.007092117354708267 |
| 0.00814241548328122 |
| 0.009208714413183598 |
| 0.010293514834327173 |
Видим, что она достаточно плавно и медленно возрастает возле нуля. Исходя из этого, мы в праве предположить, что разность (n+1)-го и n-го значений функции близка к её производной: 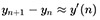 .
.
Учитывая это, наша исходная функция примет вид: 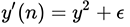 , что является простейшим дифференциальным уравнением первого порядка. Решая его (например, методом разделения переменных), получим:
, что является простейшим дифференциальным уравнением первого порядка. Решая его (например, методом разделения переменных), получим: 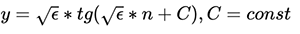
Вспоминаем нашу цель — поиск нуля. Данное выражение равно нулю только в двух случаях: либо квадратный корень из ε равен нулю — невозможно по определению, либо тангенс равен нулю. Пренебрегая константой C: 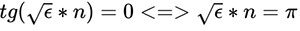 . Это подтверждает то, что мы сегодня увидели:
. Это подтверждает то, что мы сегодня увидели:
| ε | n√ε |
|---|---|
| 0.01 | 3.0 |
| 0.0001 | 3.12 |
| 0.000001 | 3.140 |
| 0.00000001 | 3.1414 |
Видно, что множитель √ε ставит ту самую запятую в нужное место.
Заключение
Построение числа Пи данным методом является, наверное, самым неэффективным способом: нужно проделать 314160 итераций для того, чтобы получить 3,14160. Кроме того, метод не обладает высокой точностью в силу больших погрешностей вычислений.
Однако нам удалось соединить две, казалось бы, несоединимые точки: фрактал и отношение длины окружности к длине её диаметра.
Комментарии (1)
6 августа 2016 в 18:58
0↑
↓
> На практике договорились: если функция (вышеприведенная) в ходе итерации превосходит значение 2, то она 100% не ограничена.Это не «договорились», это теорема.
