Анонимная сеть с теоретически доказуемой моделью на базе увеличения энтропии24.06.2023 04:16

Введение

Начну пожалуй издалека. В последние буквально два-три года, я пытаться пристально изучать сетевую анонимность с её технической стороны. В определённой степени даже появлялись успехи в этом направлении, которые постепенно кристализировались в новые направления анонимизации сетевого трафика.

Так например, до всех моих исследований и наблюдений, существовал лишь один общеизвестный вид анонимных сетей с теоретически доказуемой анонимностью — DC-сети, основанные на проблеме обедающих криптографов. К таким сетям относят, как пример, Herbivore и Dissent. После продолжительных исследований я обнаружил, что существует ещё несколько видов сетей с теоретически доказуемой анонимностью, которые работают иным образом, чем DC-сети, и каждая из которых обладает своими уникальными особенностями и характеристиками.

Теоретически доказуемая анонимность

1. Анонимные сети на базе очередей. О таковых сетях я рассказывал в большом количестве моих статей: тут, тут, тут и здесь. Наверное самой интересной их особенностью является простота реализации и примитивность доказательства, вследствие чего уже был реализован ряд программных решений с открытым исходным кодом. Т.к. о таковых сетях я рассказывал уже очень много, то мы их пропустим. Кому интересно, те могут ознакомиться, перейдя по вышеуказанным ссылкам.

2. Анонимные сети на базе увеличения энтропии. О таковых сетях я рассказывал крайне мало. Была также на хабре у меня старая статья, в которой ошибочно таковые сети я относил к седьмой стадии анонимности. Плюс к этому, данную статью было очень сложно читать неподготовленному зрителю, потому что за основу повествования я брал не формальную логику, а диалектическую, вследствие чего большую долю внимания я уделял не самой концепции анонимизации, а её развитию и движению. Поэтому в определённой мере размывались границы повествования одной темы с другой. Именно об анонимных сетях на базе увеличения энтропии мы сегодня и поговорим.

Более подробно со всеми теоретическими наработками и исследования вы можете ознакомиться тут, тут и здесь. Буду очень благодарен, если появятся какие-либо комментарии, критика, дополнения и прочее. Чем больше будет отзывов и людей участвующих в совместном исследовании, тем легче будет доходить до истины и открывать что-то новое.

Границы теоретически доказуемой анонимности

На первых порах, при встрече с таким термином как «теоретически доказуемая анонимность», можно ложно подумать, что это есть абсолютная нерушимая анонимность. Но стоит сразу же развеять этот миф. Под теоретически доказуемой анонимностью понимается «иммунитет» анонимной сети ко всем видам пассивных атак, включая атаки глобального наблюдателя, то есть лица способного просматривать весь трафик анализируемой системы с начала и до конца. Если таковая сеть способна будет представить доказательство защиты от всех пассивных наблюдателей (а это сделать достаточно легко просто сведя все действия атакующих к глобальному наблюдателю), то данную сеть можно именовать теоретически доказуемой.

Не все анонимные сети на такое способны, например Tor, I2P, Mixminion и большинство других, менее популярных, не могут этим похвастаться. В основном они базируются на более слабой модели угроз, в которой присутствует принцип федеративности располагаемых узлов, и как следствие, происходит «размытие» глобального наблюдателя на несколько разрозненных локальных наблюдателей (чаще всего под таковыми предполагаются государства). Единственными широко известными (в плане научных исследований) анонимными сетями являются сети на базе проблемы обедающих криптографов (DC-сети).

Тем не менее, когда мы говорим о теоретически доказуемой анонимности, мы предполагаем защиту исключительно от пассивных наблюдателей. Но что если существуют активные наблюдатели, которые не только могут смотреть за трафиком сети, но и всяческим образом редактировать его, отключать узлы из сети, прикидываться другими узлами и прочее? В таком случае, теоретически доказуемые сети должны обладать дополнительными улучшениями. Так например, чистые DC-сети хоть и являются теоретически доказуемыми, тем не менее, легко подвержены активным атакам, если сама их архитектура будет базировать на принципе «запрос-ответ».

Пример активной атаки (запрос-ответ)

Плюс к этому, у теоретически доказуемой анонимности также существуют границы в прикладном использовании. Под данный пункт лучше всего подходит цитата:

За безопасность приходится платить, а за ее отсутствие — расплачиваться.

(Уинстон Черчилль)

И раз мы говорим о теоретически доказуемой анонимности, то мы платим вдвойне, а именно производительностью и масштабируемостью. Какие бы мы сети с теоретически доказуемой анонимностью не взяли, везде будут присутствовать одни и те же проблемы. Так например, сети с теоретически доказуемой анонимностью очень плохо масштабируются, они часто способны функционировать лишь в пределах малых групп пользователей, допустим 50–100 человек. Чем больше становиться сеть, тем менее она становится «юзабельной». Плюс к этому, теоретически доказуемая анонимность несёт всегда какой-либо вид накладных расходов «сверх того», как например искусственные задержки в связи, большое количество спама или периоды генерации информации, из-за чего некоторые виды коммуникаций просто становятся недоступными — потоковая связь, стриминговые сервисы, видео-чаты и прочее.

Таким образом, теоретически доказуемая анонимность — это крайне радикальный подход к анонимизации трафика, без компромиссов, игнорирующий производительность и масштабируемость системы, и ставящий в приоритет исключительно и только её анонимность.

Модель на базе увеличения энтропии

И теперь, как только мы рассмотрели, что представляет собой теоретически доказуемая анонимность, мы можем приступать к рассмотрению анонимной сети на базе увеличения энтропии. Скажу сразу, данная модель очень эзотерическая, в том простом смысле, что её правильная (именно правильная) программная реализация крайне проблематична. Она хороша в теории, но на практике может приводить к фатальным проблемам деанонимизации.

Когда я исследовал анонимность, то сети на базе увеличения энтропии были первыми сетями с теоретически доказуемой анонимностью, которые я смог открыть. И по наивной простоте души я начал реализовывать сеть на её основе. В итоге, в ней было настолько много условностей, что уже во всех этих реализованных дебрях найти ту самую теоретическую доказуемость со временем становилось почти нереально. И это даже не из-за «говнокода», а как раз из-за её теоретических особенностей. В последствии, как только была открыта новая сеть с теоретически доказуемой анонимностью (на базе очередей), я переписал код на неё, сократив его как минимум вдвое.

И так, давайте приступать. Предположим, что существует три субъекта {A, B, C} и существует глобальный наблюдатель, целью которого является определение отправителя и получателя в сети. Предположим также, что все субъекты данной системы не заинтересованы в деанонимизации друг друга (эта условность будет служить лишь упрощением, на практике она в полной мере не обязательна). Анонимизация здесь строится на итеративной схеме, иными словами, чем больше вы будете отправлять сообщений, тем лучше качество анонимности будет становиться.

Предположим, что сеть базируется на схеме запрос-ответ, иными словами, когда один пользователь отправит запрос, то другой пользователь должен будет на него ответить.

Предположим, что мы являемся субъектом A, а получателем для нас будет являться субъект C. Мы знаем публичные ключи всех пользователей {B, C}. Шифрование происходит публичным ключом получателя. Предполагается, что никто не сможет расшифровать сообщение кроме узла обладающего приватным ключом. Чтобы отправить сообщение M, нам необходимо проделать одно из следующих действий с вероятностью ½:

1. Зашифровать M открытым ключом пользователя C и отправить шифрованное сообщение EC (M) всем пользователям сети, то есть пользователям B и C.

   ИЛИ

2. Зашифровать M дважды, сначала открытым ключом пользователя C, а затем открытым ключом пользователя B и отправить шифрованное сообщение EB (EC (M)) всем пользователям сети, то есть пользователям B и C.

Пример программного кода на языке Go для множественного шифрования.

import (
	"bytes"
)
func RoutePackage(sender *PrivateKey, receiver *PublicKey, data []byte, route []*PublicKey) *Package {
	var (
		rpack  = Encrypt(sender, receiver, data)
		psender  = GenerateKey(N)
	)
	for _, pub := range route {
		rpack = Encrypt(
			psender, 
			pub,
			bytes.Join(
				[][]byte{
					ROUTE_MODE,
					SerializePackage(rpack),
				},
				[]byte{},
			),
		)
	}
  return rpack
}

На первый взгляд кажется, что получилась какая-то ересь. Во-первых, глобальный наблюдатель априори знает, что пользователь A является отправителем информации M, потому как таковой является инициатором связи. Во-вторых, предполагается, что глобальный наблюдатель также знает внутренний механизм анонимизации трафика, а потому знает саму условность ½. Как следствие, если после отправленного сообщения последует сразу следующее и на этом моменте вся связь прервётся, то тот, кто переправит сообщение — является истинным получателем, сгенерировавшим ответ. Таким образом, на первый взгляд кажется, что эта схема обречена на провал.

Но мы держим в голове тот факт, что схема анонимизации итеративна и с каждым проходом лишь увеличивает анонимность. Пока что мы проигнорируем первый пункт с инициатором связи и попытаемся рассмотреть второй пункт. Действительно, если связь прервётся, то глобальный наблюдатель сможет узнать кто являлся получателем сообщения. Но теперь, что если связь будет продолжаться, хотя бы ещё одну итерацию, то насколько увеличится анонимность?

Для лёгкости восприятия, мы теперь будем исходить из лица внешнего глобального наблюдателя. Я буду указывать (A → B) как факт отправления, что A отправил B информацию. (ИЛИ) будет говорить о неопределённости со стороны наблюдателя.

Если мы далее продлим связь на плюс одну итерацию, то итоговая схема будет выглядить следующим образом:

1. (A → B ИЛИ A → C) = запрос (1)
   [Внешний наблюдатель знает лишь факт отправления и то, кто отправил сообщение — A, но пока не знает кто является получателем]

2. (B → A ИЛИ C → A) = ответ (1)
   [Внешний наблюдатель знает, что с вероятностью ½ пакет мог быть зашифрован лишь единожды и тогда B или C сразу отправит пользователю A ответ]

   ИЛИ

   (B → C ИЛИ C → B) = маршрутизация (1)
   [Внешний наблюдатель знает, что с вероятностью ½ пакет мог быть зашифрован дважды и тогда B или C будет являться маршрутизатором к C или B соответственно]

3. (B → A ИЛИ C → A) = ответ (1)
   [Внешний наблюдатель знает, что с вероятностью ½ пакет мог быть зашифрован дважды и тогда B или C после этапа маршрутизации отправит пользователю A ответ]

   ИЛИ

   (B → A ИЛИ B → C ИЛИ C → A ИЛИ C → B) = запрос (2)
   [Внешний наблюдатель предполагает, что ответ мог быть уже выдан на этапе 2., а на этапе 3. мог быть сгенерирован совершенно новый запрос]

Всё, как только вступает в действие новая итерация, а конкретно новый запрос — увеличивается энтропия, как мера неопределённости, ровно на 1 бит. В то время как раньше, до второго запроса внешний наблюдатель мог со 100% вероятностью определить отправителя, то теперь вероятность определения отправителя составляет 50% (из B и C), как только начинается вторая итерация запросов.

При этом, новая итерация запроса рушит уверенность в получателе первой итерации, потому как происходит пересечение первой незавершённой итерации запрос-маршрутизация-ответ со второй итерацией запрос. Таким образом, энтропия, по-факту увеличивается «авансом» к отправителю, потому как сначала она увеличивается для получателя, а только потом переходит на отправителя. Иными словами, если мы уверены, что цепь событий продолжится, то на втором этапе для получателя будет повышена энтропия на 1 бит, и только потом, на следующем — третьем этапе, энтропия будет повышена для отправителя.

Таким образом, хоть при первой итерации мера неопределённости равнялась 0 бит, но как только достигается вторая итерация, неопределённость увеличивается на бит и как следствие, делит ранее 100%-ую вероятность вдвое. Вышеописанную схему можно представить ещё более лёгким образом, в виде перекрытия запросов и ответов:

1. запрос (1)-ответ (1)-запрос (2)-ответ (2)

2. запрос (1)-маршрутизация (1)-ответ (1)-запрос (2)

В таком случае, мы видим, что запрос (1)=запрос (1) в любом случае равны друг другу и как следствие вероятность определения истинности равна 100%. Далее, как только начинается противоречие между первым и вторым определением — зарождается неопределённость, но только «авансом», не окончательно. Таким образом, на этапе ответ (1)=маршрутизация (1) мы уже не знаем какая конкретно происходит операция со стороны получения ответа. Если идти далее, как только появляется запрос (2)=ответ (1), то мы уже не сможем со 100% вероятностью утверждать, что не происходит совершенно нового запроса.

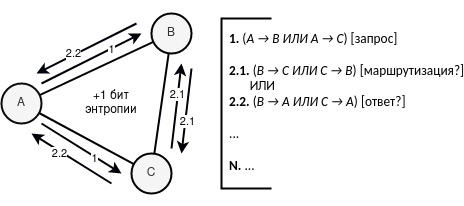
Рисунок 1. Увеличение энтропии на единицу

Если таким же образом продолжать цепь событий, то энтропия будет каждый раз увеличиваться на единицу. Визуально это можно изобразить на Рисунке 1. В результате, глобальному наблюдателю остаётся лишь догадываться кто является отправителем и получателем, и с каждым разом вероятность определения старых запросов будет постепенно «растворяться» во множестве новых.

В вышеописанном примере, мы всегда делали предположение, что запрос (2) появляется исключительно последовательно, после запрос (1). На самом же деле, такому запросу (2) ничего не мешает появляться на любом другом этапе. Так например, даже если запрос (1) и запрос (2) появились одновременно, и как следствие, глобальный наблюдатель уже знает истинных отправителей информации (инициаторов), то это ничего не говорит о получателях этой самой информации. Наблюдателю будет всё также проблематично найти получателей за счёт «слияния» нескольких запросов, и как следствие — проблематично найти будущих отправителей. Удобно было показать, что запрос (2) способен влиять не только исходя из начала или середины связи, но и в самом неудобном случае — из её окончания.

Как раз за счёт подобных «параллельных вычислений» сеть на базе увеличения энтропии является уникальной, т.к. все другие сети с теоретически доказуемой анонимностью в той или иной мере последовательны в своих запросах!

Что делать, если цепь событий прекратится?

На самом деле, чтобы цепь событий не прекращалось, не нужно как таковое активное сообщество, которое бы каждый раз, каждую секунду генерировало новую информацию. Вполне достаточно искуственной генерации сообщений по случайному периоду. В такой концепции предполагается, что любой запрос, ответ или маршрутизация может являться ложной. И как следствие, ложная информация хоть и отправляется точно также всем участникам, но никто из участников не сможет расшифровать сообщение. В итоге, это сообщение сама система просто «забудет», т.к. никто не будет на него отвечать.

Но в этой автоматизированной концепции очень важна своевременность сгенерированной информации. Так например, будет не очень хорошо, если ложная информация сгенерируется только спустя минуту после всей итерации запрос-ответ или запрос-маршрутизация-ответ. В таком случае, итерация не наберёт необходимой энтропии и как следствие, не приведёт к неопределённости отправления-получения информации. В таком случае, нам необходимо ввести ещё ряд условностей и определений.

1. Задержка T[0; N]. В такой концепции свойство задержки T[0; N] применяется для аккумулирования энтропии. Чем больше участников сети становится, тем больший прирост энтропии способен обеспечиваться в интервале T[0; N]. При отсутствии данного параметра вероятность нулевого прироста энтропии увеличивается прямо пропорционально уменьшению мощности спама (активности) сети. Таким образом, максимальный диапазон задержки N должен устанавливаться не меньше среднего времени генерации нового пакета в системе.

2. Мощность спама |St| —  количество сгенерированных уникальных пакетов в системе за определённый период времени t совершённый разнородными (никак не связанными между собой общими целями и интересами) участниками сети. Из данного определения мощность спама не может превышать количество её участников ни в какой выбранный промежуток времени, потому как два и более сгенерированных пакета одним пользователем будут считаться за один, по причине однородности узла к самому себе. Уровень заспамленности становится в некой мере ключевым фактором безопасности, т.к. «размывает» связь между истинными субъектами посредством перемешивания множества объектов в сети.

Мощность спама |St|, где M — множество всех узлов в сети, Q — функция выборки списка подмножеств узлов, подчиняющихся одному лицу или группе лиц с общими интересами, P — период генерации пакета на базе выбранного узла, L = Q (M), G: {0,1}→{0,1} = x+1 (mod 2), F: N⋃{0}→{0,1}=⌈x/(1+x)⌉

Если t представлено как НОК от всех P (Lij) → НОК (P (L11), P (L12), …, P (L21), P (L22), …, P (Lnm)), то в заданный промежуток времени мощность спама обретает своё максимальное значение |St| = |L|. Примером может служить таблица вычисления мощности спама при L = [{A, B}, {C}, {D}],  P (A) = 1, P (B) = 2, P© = 3, P (D) = 2, где НОК (P (A), P (B), P©, P (D)) = 6.

Как обстоят дела с активными атакующими?

В примитивном виде, сеть на базе увеличения энтропии уязвима к активным атакующим. Например, если один из пользователей {A, B, C} является активным атакующим, допустим это будет узел A, а также он кооперирует с пассивным глобальным наблюдателем, то он может совершать атаку с целью сопоставления идентификатора ID с сетевым адресом IP для одного из {B, C} способом запроса-ответа. Узлу A достаточно отправить сообщение одному из узлов по ID, далее подождать ответ, передать структуру пакета пассивному наблюдателю, который укажет из какой точки впервые был создан такой пакет. Таким образом, ID будет сопоставлен с IP адресом, и как следствие один из субъектов {B, C} будет деанонимизирован.

Сама атака базируется на том, что весь маршрут выстраивает исключительно инициирующая сторона — отправитель, в то время как получатель просто и слепо следует протоколу «отправить как указано в инструкции». На самом же деле, получатель должен иметь ровно те же функции, что и отправитель — создавать вероятностную маршрутизацию. В таком случае, сам протокол взаимодействия будет выглядить как на Рисунке 2.

Рисунок 2. Обобщённая схема передачи информации в анонимной сети на базе увеличения энтропии

При ранее анализируемых задержках и при вероятностной маршрутизации со стороны получателя мы становимся способными противостоять вышеописанной атаке. Как только будет получен запрос одним из субъектов B или C, запрос попадёт в этап ожидания T[0; N], после чего будет произведена либо маршрутизация, либо ответ. Задержка необходима по причине ответа без маршрутизации, потому как при самой задержке повысится мощность спама, и как следствие, повысится мера неопределённости. Более визуально это изображено на Рисунке 3.

Рисунок 3. Неопределённость выявления получателя при атаке сопоставления связей между сетевой и криптографической идентификациями на инициирующей стороне

Какие подводные камни?

Подводных камней здесь огромное количество.

1. Во-первых, если будет существовать кооперация активных атакующий, как внутренних, так и внешних, то отключение узлов от сети и ping оставшихся может нарушать анонимность субъектов. Решением здесь может стать держание поточной связи с какими-либо ещё участниками сети, с условием, что если их отключат от сети, то связанные с ними узлы просто уйдут в deadlock и перестанут отвечать на какие-либо запросы. Решение не идеальное потому как существует второй пункт.

2. Во-вторых, децентрализованные сети являются крайне динамичными структурами, узел может появляться на короткое время, может пропадать на продолжительное, может перемещаться, может менять IP и т.д. В таком случае, выстроить deadlock связь с другим пользователем будет проблематично.

3. В-третьих, как было указано ранее, все ныне известные теоретически доказуемые анонимные сети не могут эффективно масштабироваться. Анонимные сети на базе увеличения энтропии тому не исключение. Чем больше пользователей — тем больше спама, тем больше нагрузки на каждого отдельного пользователя. Иными словами, нагрузка увеличивается линейно.

4. В-четвёртых, множественное шифрование должно быть неотличимо от единичного шифрования, иначе можно будет выявить по разнице размеров пакетов состояние субъекта — маршрутизация или ответ.

Заключение

Вот мы и рассмотрели сеть с теоретически доказуемой анонимностью на базе увеличения энтропии. За счёт своей эзотеричности в плане итеративного увеличения неопределённости, она интересна и равносильно сложна в программной реализации из-за массы выдвигаемых условностей. Тем не менее, таковая сеть является вполне себе новым видом анонимных сетей, отличным от DC-сетей (на базе задачи обедающих криптографов).

© Habrahabr.ru