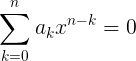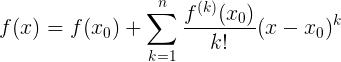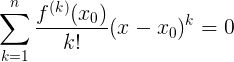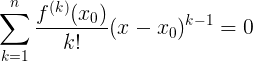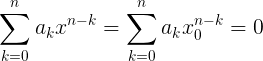Алгоритм нахождения эквивалентных точек оси абсцисс функции многочлена

Уважаемые хабровчане, приветствую! Продолжаем цикл околоматематических статей, предыдущая расположена тут. Напомню, что я лишь дилетант математики, занимающийся её морально-эстетической стороной, и мои идеи могут показаться вам неинтересными/бесполезными/etc. Итак:
Для начала верным шагом будет введение аксиоматики на счет термина «эквивалентности» в данном контексте:
- Если некоторая координата оси абсцисс
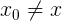 из числового множества удовлетворяет следующему условию:
из числового множества удовлетворяет следующему условию: 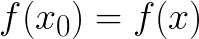
То считается, что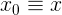 (то есть
(то есть  эквивалентна
эквивалентна 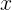 )
)
Такая аксиоматика в рамках этой статьи удобства ради, и, строго говоря, не совсем корректна.
И сразу бы неплохо ответить на традиционный вопрос: «извините, а зачем это надо?». Отвечаю — как минимум, для поиска остальных корней уравнения многочлена (перейдя от уравнения к функции), зная лишь один корень. А также многообразие менее очевидных вещей. Сейчас мы и займемся разрешением этой задачи, а затем приведем алгоритм в общем виде. Для заинтересовавшихся милости прошу под кат.
Отметим, что мы будем работать над следующим классом функций:
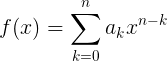
Для тех, кто не знает, что такое сигма, нужно пояснить, что это равносильно следующему:
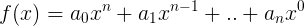
Это ни что иное, как общий вид функции, представляющей собой многочлен.
Давайте наконец сформируем понятную задачу на конкретном примере, чтобы лучше понимать происходящее. Итак, имеем уравнение многочлена третьей степени, то бишь кубическое:
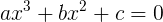
Задача: зная один из корней уравнения (из любого числового множества — будь он хоть рациональным, хоть комплексным и т.д.), найти остальные корни уравнения. Да не просто найти, а путем решения уравнения меньшей степени!
Что же, самое время перейти от уравнения к функции:
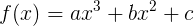
А дальше, забавы ради, найдем все ненулевые производные функции:
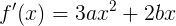
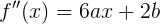
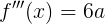
Ну раз уж нашли, давайте и в ряд Тейлора функцию разложим (где
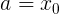 ):
): 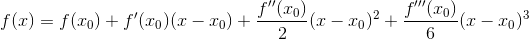
Дальше вспомним вышеописанную аксиоматику эквивалентности
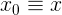 для нашего контекста:
для нашего контекста: 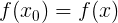 [в силу равенства справедливо и
[в силу равенства справедливо и 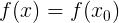 ]
]Ничего не напоминает? Правильно! Это же первый член разложения в ряд Тейлора для нашей функции. Тогда, очевидно, чтобы равенство было тождественным, остальные члены разложения должны обратиться в ноль. Иными словами:
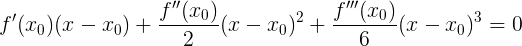
Воспользуемся следующим очевидным правилом:
- Произведение равно нулю тогда и только тогда, когда хотя бы один или несколько множителей равны нулю.
А мы как раз можем множитель
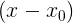 вынести за скобки:
вынести за скобки: 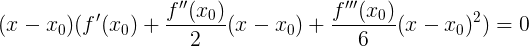
Тогда:
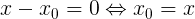
не подойдет, т.к.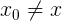 , ибо будет тавтология вида
, ибо будет тавтология вида 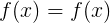
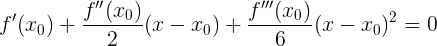
Вот второй случая обращения в произведение в ноль нам вполне подойдет! Давайте же скорее подставим производные:
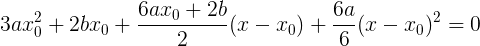
Подсократим немного:
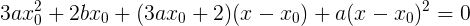
И о чудо! Уравнение получилось второй степени (квадратное), в то время как исходное уравнение было кубическим (третей степени).
Решая его относительно
 получим следующие корни:
получим следующие корни: 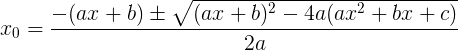
Очевидно, из этого для нашей функции следует следующее:
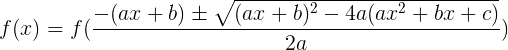
Что это нам дает для нашего уравнения? А то, что зная один из корней уравнения, мы сможем найти остальные два (причем за квадратичную сложность).
Следствие: зная один из корней уравнения степени
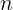 , можно понизить степень уравнения до
, можно понизить степень уравнения до 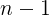 , причем корень может быть из любого стандартного числового множества.
, причем корень может быть из любого стандартного числового множества.Давайте рассмотрим на более конкретном примере:
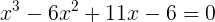
Я знаю, что из корней искомого уравнение равен
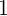 . А если представить уравнение как кубическую функцию (по алгоритму, описанному выше), то получим следующее:
. А если представить уравнение как кубическую функцию (по алгоритму, описанному выше), то получим следующее: 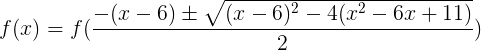
График выглядит следующим образом:

Тогда для нашего корня
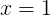 :
: 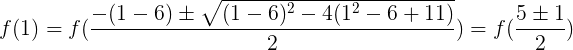
То есть:
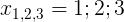
Таким образом, мы нашли остальные два корня кубического уравнения путем решения квадратного уравнения. В общеизвестных кругах есть метод деления уголком, которые позволяет также понизить степень. Но он работает только при целочисленных коэффициентах (т.е. рациональные придется приводить к целым, а комплексные вообще не возможно).
Также интересен тот факт, что из подобной формулы «эквивалентности» следуют условия (не)монотонности для многочлена n-ой степени. Сформировать его можно так:
При обнаружении в многочленечетного радикала
(где
— любое подкоренное выражение) можно сформировать следующее свойство:
Если при любыхвыполняется неравенство
, то график искомой функции является монотонным на всем множестве
. Также справедливо и обратное, если
.
Почему так? Да потому что если оное не выполняется, то мы просто напросто не сможем вычислить
 из-за ОДЗ подкоренного выражения.
из-за ОДЗ подкоренного выражения.Пожалуй, настало время сформировать общий алгоритм нахождения эквивалентных точек оси абсцисс функции многочлена.
Имеем уравнение в виде многочлена произвольной степени общего вида:
Перейдем от уравнения к функции:
Разложим функцию в ряд Тейлора, где:
Нам необходимо найти, следовательно:
Тогда:
не подойдет, т.к., ибо будет тавтология вида
Решим уравнение относительно(степень которого меньше исходного), корни которого и будут эквивалентностью
.
Теперь, в частности, справедливо следующее:
Эквивалентные точки найдены.
Также не забываем про условие (не)монотонности и другие разнообразные следствия из искомого алгоритма. Также стоит отметить, что обычно условия монотонности определяют по ОДЗ радикала корней уравнения
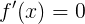 . Напомню, что так можно искать не только «остальные корни», но и любые
. Напомню, что так можно искать не только «остальные корни», но и любые  , такие что:
, такие что: 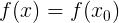
Ещё стоит упомянуть что, согласно теореме Абеля — Руффини, алгоритм будет работать только до многочлена общего вида 5-ой степени включительно (т.к. корни уравнения высших порядков больше четвертой нельзя представить в виде рациональных функций (корней то бишь и т.д.).
Поставленную воскресную задачу мы выполнили, за сим отклоняюсь.
Спасибо за внимание!