Алгоритм Брезенхема в паяльной печи — теория
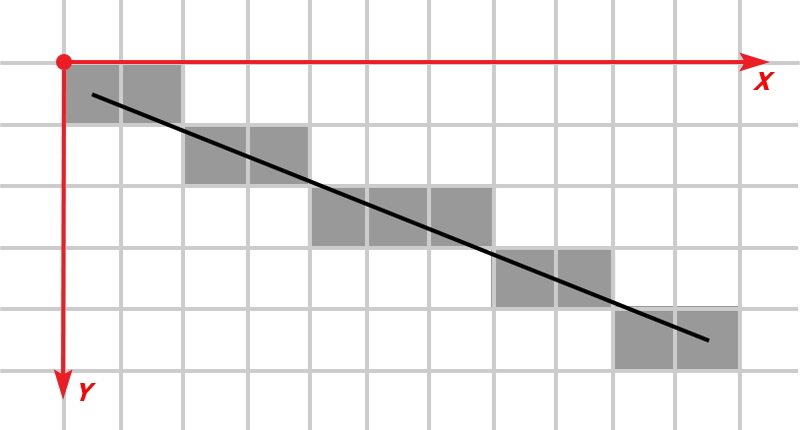Алгоритм Брезенхема является одним из старейших алгоритмов в машинной графике. Казалось бы, как можно применить алгоритм построения растровых прямых при создании домашней паяльной печи? Оказывается можно, причем с очень достойным результатом. Забегая вперед, скажу, что данный алгоритм очень хорошо скармливается маломощному 8-битному микроконтроллеру. Но обо всем по порядку.Алгоритм Брезенхе́ма — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Суть алгоритма заключается в том, чтобы для каждого столбца X (см. рисунок) определить какая строка Y ближе всего к линии, и нарисовать точку.Теперь посмотрим как подобный алгоритм поможет нам при управлении ТЭНами в электропечи.
ТЭН питается от сетевого напряжения 220В/50Hz. Взглянем на график.
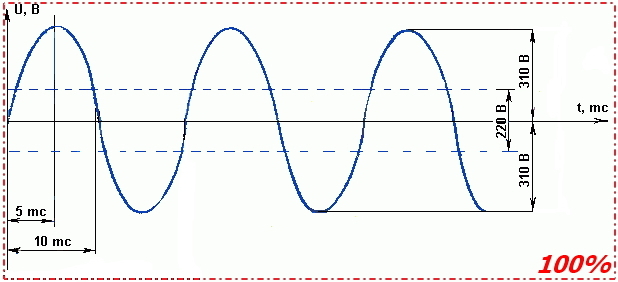При подаче такого напряжения в чистом его виде на вход электронагревателя мы получим на выходе 100% мощность нагрева. Все просто.
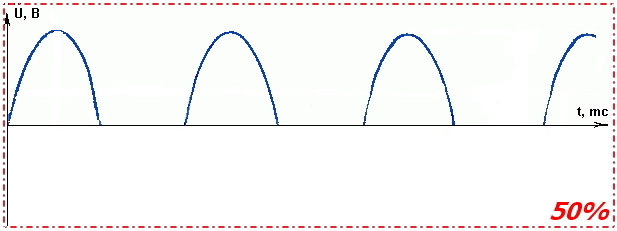Что будет если подать на вход ТЭНа только положительную полуволну сетевого напряжения? Правильно, мы получим 50% выходной мощности нагрева.
Если подать каждую третью полуволну, мы получим 33% мощности.
В качестве примера возьмем 10% градацию выходной мощности и временной отрезок в 100 мс, что равносильно 10 полуволнам сетевого напряжения. Нарисуем сетку 10×10 и представим, что ось Y это ось значений выходной мощности. Проведем прямую от 0 до необходимого значения мощности.
Прослеживаете зависимость? Увеличив временной отрезок до 1 сек, можно получить градацию выходной мощности в 1%. Получится сетка 100×100 со всеми вытекающими.
А теперь о приятном: Алгоритм Брезенхема можно построить в цикле таким образом, чтобы на каждом шаге по оси X просто отслеживать значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу (читай — пропускаем одну полуволну напряжения), одновременно уменьшая значение ошибки на 1.
Такой подход легко сводится к циклическому целочисленному сложению (об этом позже, при описании алгоритма работы МК в следующей статье), что несомненный плюс для микроконтроллеров.
Я намеренно не стал грузить вас формулами. Алгоритм элементарный, легко гуглится. Я лишь хочу показать его возможность применения в схемотехнике. Для управления нагрузкой будет использоваться типовая схема подключения симисторной оптопары MOC3063 с детектором нуля.
При таком подходе есть ряд преимуществ.
Отсутствуют помехи в сети из-за частых коммутаций большой нагрузки, включение/выключение будет происходить в моменты перехода напряжения через ноль. Очень простой алгоритм — все вычисления сводятся к работе с целыми числами, что хорошо для микроконтроллера. Нет необходимости городить детектор перехода напряжения через ноль (привет MOC3063). Даже если МК будет просто дергать ногой по таймеру, открывая оптопару, ошибка будет не критичной. Продолжение следует.
