Аксиома выбора и принципиальные ограничения человеческого разума11.01.2021 19:17

Когда я учился в институте, то очень не любил философию. Дело не только в том, что тогда это была марсистко-ленинская философия — просто я не видел смысла в этом бессмысленном нагромождении слов. Уже много позже я обнаружил, что увлекаюсь именно философией -, но философией науки.

На мой взгляд, у философии должен быть конкретный объект рассмотрения: бесконечности в теории множеств, трансфинитные числа, теории и доказуемость, гипотеза математической вселенной Макса Тегмарка. И тогда есть реальный прогресс (например, теорема Геделя), а слова просто облегают каркас, задаваемый конкретикой. Иначе получается попытка построить конструкцию из жидкой манной каши, какой-то интеллектуальный онанизм.

Георг Кантор, положивший начало теории множеств и открывший разницу типов мощностей (по-английски cardinalities), на мой взгляд, куда больший философ, чем Кант и Гегель. Вы можете не вынимать ложечку из чашки кофе, когда пьете его и съедать яблоко с огрызком, но знать отличие счетного множества от континуума обязаны, если вы связаны с IT или любой технической сферой.

Одной из интересных в философском плане вещей является знаменитая (в узких кругах) Аксиома Выбора (AC) — внешне совершенно безобидная, но с чудовищными последствиями. Аксиома утверждает, что, если существуют два непустых множества, то существует и множество, содержащее ровно по одному элементу из обоих:

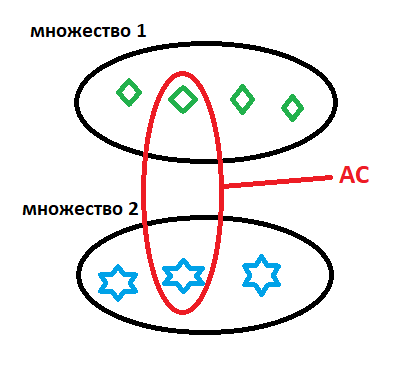
Если одно из этих множеств содержит только один элемент, то он всегда и будет выбираться и работать как крючок, «выуживая» из второго множества элементы. Если после каждого такого акта выбора мы будем выбранные элементы изымать, то с помощью данной процедуры мы можем разобрать любое множество по элементам.

Парадоксы Аксиомы Выбора

Как ни странно, «чистая» теория множеств не утверждает, что любое множество можно «разобрать на части». Она утверждает, что для любого множества можно проверить, содержится ли некий элемент в нем или нет (отношение $\in$ ). Интуитивно ясно, что конечное или счетное множество (например, множество натуральных чисел) можно разобрать на элементы. Для континуума это уже совсем не очевидно.

Аксиома Выбора известна тем, что рождает чудовищ. Чудовища называются intangibles — объекты, существование которых может быть доказано, но ни один конкретный пример не может быть приведен. Классическим примером такого чудовища является Парадокс Банаха Тарского.

Сферу можно разрезать на шесть частей так, что после поворотов из них можно слепить две сферы такого же диаметра — без зазоров и пустот! А откуда же взялся лишний объем? спросите вы. Для того, чтобы вычислить объем, объект должен быть в какой-то степени гладким. Части в данном случае бесконечно сложны по построению, и их объем неопределен. А как безобидно все начиналось!

Разумеется, многим математикам такое поведение Аксиомы Выбора пришлось не по вкусу. Так как математики творцы своих собственных миров, они могут делать все, что захотят. Самым очевидным было ограничить работу AC только счетными множествами, где все очевидно. Но это связывало руки тем, кто работал с вещественными числами, а топологию просто убивало. Поэтому есть целый ряд «ослабленных» вариантов AC (например, Аксиома Зависимого Выбора), или альтернативных вариантов, например, Аксиома Детерминизма.

Какое-то время я тоже считал, что ослабленные аксиомы лучше, хотя они так лимитируют наши знания. Однако потом я пришел к выводу, что проблема совсем не в аксиоме выбора, а в нашем сознании. Наш мозг может работать с конечным количеством информации. Этого количества информации достаточно, чтобы охарактеризовать элемент из бесконечного, но счетного множества элементов. С большими мощностями проблемы — для выбора из них может потребоваться бесконечное количество информации.

Например, пусть у нас есть континуум вещественных чисел [0,1]. Уберем из него все числа, которые мы можем определить строкой, например, '0.324443', '⅓', '1/pi' (pi лучше определить через бесконечные ряды), 'min корень уравнения…' (причем в последнем случае не важно, умеем ли мы это уравнение решать). Важно что число строк счетно, а вещественных чисел больше, так что в итоге останется странное множество… В нем еще осталось почти столько же элементов, сколько и было, но ни один элемент нельзя привести в качестве примера. Ведь чтобы привести пример, его надо уметь записать строкой, а все такие числа вырезаны!

Структура чудовищ, таким образом, представляется такой:

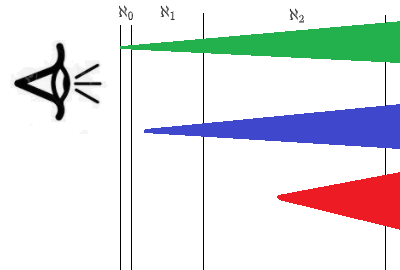
В хорошем случае (показано зеленым), сущности существуют и имеют своих представителей на тонкой пленке счетных множеств. Мы видим эти сущности 'на поверхности' и нам хорошо. Более сложные сущности могут прятаться глубже — на уровне континуума (пример с отрезком выше) и еще глубже (парадокс Банаха Тарского- показано красным). У таких сущностей нет представителей в тонкой пленке счетных множеств (а собственно, почему они всегда должны там быть?) -, но это исключительно наши проблемы!

Сложные инопланетяне

В теплых ламповых фильмах инопланетян изображают так:

То есть со всеми людскими чертами с небольшими изменениями. Инопланетяне даже говорят по-английски! Это, конечно, очень мило, но крайне упрощено. Тут попытка более серьезна:

Однако, попытаемся смастерить более продвинутых инопланетян. Итак, что мы можем сказать о человеке?

наш мозг содержит конечное количество информации
наши сообщения, слова, фразы, тоже передают конечное количество информации
это позволяет выбирать элементы из бесконечных, но счетных множеств $\aleph_0$
Аксиома выбора для счетных множеств нам кажется очевидной
Мы живем в пространстве времени, которое континуум ( $\aleph_1$ )

Давайте сделаем апгрейд — 'one level up' в иерархии мощностей:

их мозг содержит бесконечное, но счетное количество информации
их сообщения тоже передают бесконечное счетное количество информации. Например, одно слово может содержать вещественное число с бесконечной точностью со всеми его цифрами после запятой
это позволяет выбирать элементы из континуума $\aleph_1$
Аксиома выбора для континуума им кажется очевидной
Парадокс Банаха Тарского им не кажется парадоксом. Идея им интуитивна понятна, хотя пример они по прежнему привести не могут.
Эти существа существуют в мире, где пространство/время по крайней мере $\aleph_2$

Последние два пункта требуют пояснений. Для разбиения сферы в парадоксе БТ аксиома Выбора используется континуум раз — то есть пример разбиения содержит континуум информации — больше, чем эти инопланетяне могут выразить словами. Тем не менее сама идея им понятна. У людей (one level down) концепция 'бесконечная последовательность натуральных чисел, из которых случайным образом изъято по одному числу из каждой десятки' не вызывает затруднений, хотя мы и не могли бы записать полный пример такой последовательности (так как она бесконечна)

Наше пространство время (континуум) слишком бедно, чтобы вместить таких существ. Поэтому мы не могли бы с ними встретиться. Но они, безусловно, существуют, так как, согласно Математической Гипотезе Тегмарка, все математические миры всегда реализуются. И если наш мир с континуумом пространства времени и несколькими страницами формул, определяющих физические законы, дал возможность существования существ с сознанием, то невозможно представить, что существа с более высоким типом сознания не существуют в более 'богатых' мирах.

Cognitive Closure

Извините, не знаю, как это будет по-русски. Почитать можно здесь. Явления мира 'продвинутых инопланетян' выше являются для нас трансцендентными. Тем не менее, если мы не можем их понять, то мы можем хотя бы как то их описать или предложить упрощенные модели. Однако ситуация может быть еще хуже. Возможно, есть концепции, к которым мы вообще не можем прикоснуться.

Один из кандидатов является проблема сознания. Напомню диспозицию, существует ряд подходов к проблеме:

Материазизм или физикализм, он же функционализм, воззрение, что сознание 'как то' возникает из работы мозга (и, возможно, других сложных систем). Выглядят научно, но проблема со словом 'как то', потому что прогресс за сотни лет нулевой
Панпсихизм — любая частичка обладает крохой сознания. Это воззрение хорошо тем, что не требует 'возникновение' сознания — оно изначально связано с материей. Но у подхода свои проблемы
Отрицание существование сознания в принципе (упертый старик Деннетт)
New mysterianism

Последний подход — возможно, сознание и создается мозгом. Но сознание само в принципе не может и не сможет это понять. Это сможет понять только сознание более высокого уровня, и так далее. (ничего не напоминает? да, теорему Геделя)

Теория множеств дает хорошие примеры, иллюстрирующих концепцию cognitive closure — там это называется fixed points. Пусть вы суммируете единицы. 1,2,3, … 5556054, каждое следующее число больше предыдущего, есть прогресс. Но вы никогда не достигните первой счетной бесконечности $\omega_0$ . Аналогично, беря функцию 'множество всех подмножеств' — функция чудовищной силы, создающая из счетного множества континуум и так далее, вы никогда не достигните первой недостижимой мощности.

Важно, что cognitive closure не видна снизу как граница. Это не барьер. Это не сложная задача, которую вам не решить. Она вообще вам не видна — все как бы хорошо, вы можете написать еще одну статью, исследовать еще одно явление, доказать еще одну теорему. Вас никто не будет останавливать — вы просто не можете понять, что вы не способны понять. Вы не увидите проблему.