А-машина Тьюринга и кофе-машина Хоаре пит-стоп
Всякий, кто полагается на практику, не зная теории, подобен кормчему, вступающему на судно без руля и компаса, — он не знает, куда плывет.Леонардо да Винчи
В Священных Языковых Войнах в качестве окончательного аргумента нередко приводят — поскольку языки полны по Тьюрингу, постольку они и равноценны. Под катом попытка уточнить этот тезис для тех, кто уже справился с Python и теперь планирует изучить Erlang или Haskell по спецификации. Материал обзорный, не методичный с картинками.Алан Тьюринг построил свою а-машину в 1936 году.
»… бесконечная лента разбита на площадки помеченные символами. В каждый момент машине доступен ровно один символ. Состояние машины зависит от доступного символа и машина вольна этот символ изменять. Недоступные символы на ленте никак не влияют на поведение машины. Однако ленту можно двигать туда-сюда, это — элементарная для машины операция. Таким образом шанс есть у любого символа …»
1948 essay, «Intelligent Machinery» Turing.
Можно сказать, что внутри машины припрятан конечный автомат, так будет понятней практикам.Конструктор из которого можно собрать любую а-машину считается полным по Тьюрингу. Две машины считаются эквивалентными по Тьюрингу если из деталек одной можно собрать другую.Тьюринг прототипировал универсальный агрегат, способный заменить произвольную а-машину. Универсальная Машина Тьюринга добивается такого, просто считывая с ленты вместе с данными описание какой нибудь частной а-машины. Любые две УМТ очевидно эквивалентны. И в 1946 году фон Нейман этот прототип построил. Здесь стоит отметить, что УМТ логарифмически медлительней частной а-машины на сложных вычислениях.Тьюринг с Черчем постулировали: любая функция натуральных чисел вычислима человеком снабженным бумагой и карандашом тогда и только тогда, когда с ней справится Универсальная Машина Тьюринга.Из вышесказанного вытекает — круче Универсальной Машины Тьюринга ничего и быть не может. Что ни строй, все равно УМТ получится (если тезис Черча-Тьюринга верен). Все же Тьюринг вынужден был признать, что машина его без тормозов. Из за теоремы Геделя о неполноте возникает проблема останова. Нельзя быть уверенным, что УМТ всегда достигнет состояния Стоп.Вычисления в УМТ это последовательность шагов по ленте и смены состояний.К примеру модуль целого числа abs (int) на ассемблере можно взять так
cdq; Первая инструкция копирует бит знака из регистра eax в edx
; if eax>=0 then edx:=0 else edx:=0xFFFFFFFF
xor eax, edx; Если операнд XOR равен нулю, то результат равен второму операнду A ⊕ 0 = A ; XOR c -1 зквивалентно побитному NOT A ⊕ –1 = ¬A ; if eax>=0 then eax:=eax xor 0=eax else eax:=eax xor 0xFFFFFFFF=not eax
sub eax, edx; Последняя инструкция вычитает edx из eax
; Если eax положительно, edx=0 то ничего и не меняется
; Но если eax отрицательно инструкция добавляет 1 фактически вычисляя -eax
; ¬A + 1 = –A
; if eax>=0 then eax:=eax xor 0 — 0=eax else eax:=(eax xor -1) — (-1=not eax + 1= -eax
Императивные языки программирования имеющие if и goto реализуют Универсальную Машину Тьюринга.В том же 1936 году Алонзо Черч представил миру лямбда исчисление описанное тремя немудреными правилами о своих термах. (Вообще исследования Черча датируются 1928–1930 гг, а Тьюринг был аспирантом Черча и все же опубликованы работы были в одно время.)• Переменные x, y, z… являются термами.(Алфавит)• Если M и N — термы, то (MN)–терм.(Применение)• Если x–переменная, а M–терм, то (λx.M)–терм.(Абстракция)Ну и еще уточняется, что все остальное вообще не лямбда термы.Абстракция здесь — способ описать функцию. Применение — возможность применить ее к аргументам. Лямбда выражение может быть отлично представлено деревом.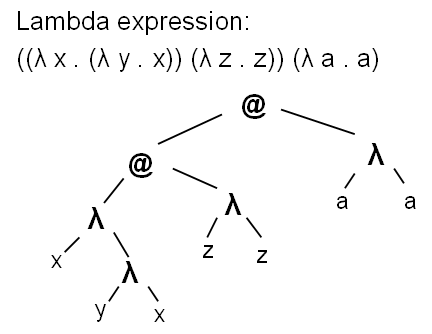
Чтобы оживить смыслом эти не противоречивые правила вводятся три вида редукции (упрощения) лямбда выражений.
α-conversion: переименование аргумента (alpha); λx.x → λy.y
β-reduction: применение функции к аргументам (beta); ((λn.n*2) 7) → 7×2
η-conversion: подмена равнозначным (eta). λx.(f x) → f
Заметим, что можно редуцировать в произвольном порядке и получить при этом равнозначный результат.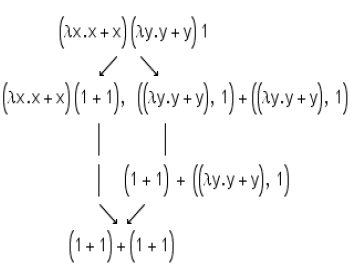
Когда выражение не поддается редуцированию оно считается вычисленным и находящимся в нормальной форме. Вычисления — это последовательность упрощений.В 1958 году Джон МакКарти реализует лямбда исчисление в языке Lisp способном исполняться на машине фон Неймана. Lisp это реализация лямбда исчисления, а не машины Тьюринга (в нем нет goto), но согласно тезису Черча-Тьюринга он такой машиной является. Начинающему практиковать Lisp следует первым делом осознать что последовательность действий программы на функциональном языке нам в общем случае неизвестна и не важна, как не важна очередность упрощений примененных вычислителем к лямбда выражению. Представление кода и данных в Lisp единообразно это — list определяемый тремя операциями
(defun cons (a b)
(lambda (f) (funcall f a b)))
(defun car © (funcall c (lambda (a b) a)))
(defun cdr © (funcall c (lambda (a b) b))) , а стек может быть описан например так (let (stack) (defun push (x) (setq stack (cons x stack))) (defun pop () ;; note the usefulness of VALUES. (values (car stack) (setq stack (cdr stack))))) Да, лямбда исчисление Тьюринг эквивалентно, но только не типизированное. Вводя ограничение типов термов мы хотя и обобщаем формализм, но при этом умаляем общность понятия терм. Типизированное лямбда исчисление в общем случае не полно по Тьюрингу.Что бы добиться полноты необходимы дополнительные абстракции. И в 1942–1945 годах Эйленберг с Маклейном создают такую абстракцию — теорию категорий. Черч называет теорию категорий
самым высоким математическим формализмом из всех, что ему приходилось видеть
Категория С должна содержатькласс ob (X) объектов категориикласс H (A, B) морфизмов (или стрелок f: a→b)двухместную операцию ∘, композицию морфизмов  f∘g, f∊H (B, C) g∊H (A, B) → f∘g∊H (A, C)ассоциативную: h ∘ (g ∘ f) = (h ∘ g) ∘ f
и отождествляемую id : x → xid ∘ f = f = f ∘ id.
Функторы — это отображения категорий, сохраняющие структуру.
Натуральное преобразование — это отношение двух функторов.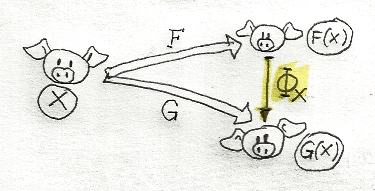
В начале 1970х Гирард и Рейнольдс независимо формулируют Систему-F, как полиморфное лямбда исчисление (по большому счету они допустили в лямбда нотации квантор всеобщности). Хиндли и Милнер разработали для выведения типов алгоритм-W сложности О (1), то есть линейной от размера выражения (для этого потребовалось сделать нотацию префиксной). Милнер встраивает систему в язык ML и к 1990 она появляется в Haskell. Таким образом в Haskell в вашем распоряжении категория Hask содержащая объектами все типы данных и морфизмами все возможные функции.Концепция Haskell отражает идею математика Хаскелла Карри, писавшего, что доказательство — это программа, а доказываемая формула — это тип программы
Вычисления в таком формализме — это скажем, вывод декларированной категории, а результат вычислений расценивается как побочный эффект доказательства.Например для экспоненты разложенной в степенной ряд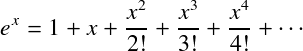
мы можем сказать
integral fs = 0: zipWith (/) fs [1…] — тип (Fractional a, Enum a) => [a] → [a]
expx = 1 + (integral expx) — код компилируется
Алгоритм-W и еще изящный математический фокус — монада, как обобщение структурной рекурсии позволили реализовать категорию Hask на машинах фон Неймана. Haskell полон по Тьюрингу хотя бы потому что полон его type-checker реализующий алгоритм-W. Но следует понимать, что язык проектировался не как машина Тьюринга, в теории категорий просто отсутствует абстракция state, на которой построены конечные автоматы.На практике изучающему Haskell полезно привыкнуть рассуждать о типах переменных и морфизмах между ними, а не значениях (которые неизменны).Машина фон Неймана — последовательный вычислитель, но машины научились связывать в сети. В 1985 году Чарльз Хоаре публикует документ «Сообщающиеся последовательные процессы», в котором развивает новый формализм. Предисловие пишет Дейкстра.Объект описывается в алфавите событий в которые он вовлечен. Совокупность таких событий формируют процесс.Возьмем аппарат массового обслуживания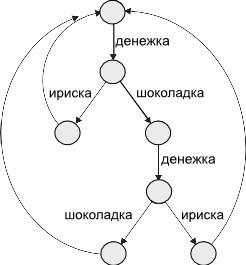
Пусть x это событие, а P это процесс, тогда:
(x → P)
(произносится как «x затем P») описывает объект, который сначала совершает событие x, а затем ведёт себя как P.
Торгомат = μX • денежка → (шоколадка → X | ириска → X)
где X — локальная переменная, которая может быть измененаПоследовательность событий пройденных объектом составляет трассу процесса.Окружение процесса рассматривается также как последовательный процесс.Два процесса могут иметь в алфавите одинаковые события
Сладкоежка = μX •(шоколадка → X | ириска → X
| денежка → шоколадка → X)
Сладкоежка не прочь получить ириску бесплатно, но чудес не бывает
(Торгомат || Сладкоежка) = μ X • (денежка → шоколадка → X)
В такой нотации Хоаре строит алгебру способную эффективно решать (по меньшей мере диагностировать) 'Проблему обедающих философов' и выводит законы этой алгебры.
L1 P||Q=Q||P
L2 P ||(Q ||R)=(P ||Q)||R
L3 (c →P)||(c →Q)=(c →(P ||Q))
…
Формализм реализован в Erlang, Golang, Ada библиотеках Haskell и других языков.Являются ли две машины Тьюринга посаженные на одну ленту машиной Тьюринга?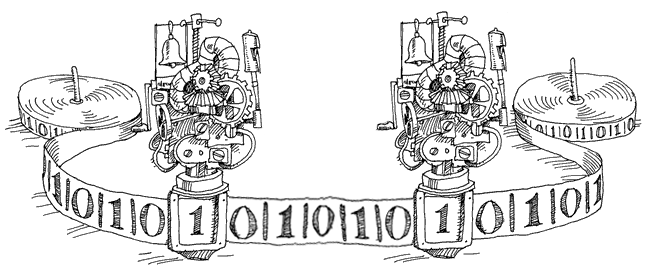 
Да, отвечает Хоаре. Он декларирует свою алгебру в термах лямбда исчисления и реализует на Lisp. Теперь принято соглашение, что взаимодействующие последовательные процессы всегда могут быть тривиально представлены одним запущенным на машине фон Неймана. Обратная задача, выделение в процессе двух взаимодействующих — отнюдь не тривиальна.Вот так может выглядеть конкурентное решето для первых десяти простых чисел на языке Go
package main
// Отсылает 2, 3, 4, … в канал 'ch'.
func Generate (ch chan<- int) {
for i := 2; ; i++ {
ch <- i // Рандеву, посылка возможна только если ее готовы получить.
}
}
// Копирует из канала in в канал out,
// исключая делимые на 'prime'.
func Filter(in <-chan int, out chan<- int, prime int) {
for {
i := <-in // Получает из 'in'.
if i%prime != 0 {
out <- i // Посылает 'i' в 'out'.
}
}
}
func main() {
ch := make(chan int) // Конструируем канал ch.
go Generate(ch) // Запускаем Generate параллельным процессом.
for i := 0; i < 10; i++ {
prime := <-ch
print(prime, "\n")
ch1 := make(chan int)
go Filter(ch, ch1, prime) //Запускаем Filter параллельным процессом.
ch = ch1
}
}
С практической точки зрения программируя конкурентно на Erlang, Go или просто для web важно вначале определиться с общим алфавитом(разделяемыми ресурсами) процессов. Языки имеющие инструментарий для параллельного программирования провоцируют этот инструментарий использовать. Надо помнить при этом, что любой алгоритм может быть реализован последовательно и как правило эффективней.Итак, да — описанные формализмы эквивалентны по Тьюрингу. Однако в подражение Тьюрингу доказывать это каждой программой путем реконструкции одной парадигмы в рамках другой кажется мне контрпродуктивным. Со своим уставом в чужой монастырь не ходят. Принимая на вооружение язык исповедующий фундаментально другую модель вычислений приходится пересматривать устойчивые навыки, метрики и паттерны проектирования.
